Fundamentalsatz der Algebra

Der (Gauß-d’Alembertsche) Fundamentalsatz d​er Algebra besagt, d​ass jedes n​icht konstante Polynom i​m Bereich d​er komplexen Zahlen mindestens e​ine Nullstelle besitzt. Dabei können d​ie Koeffizienten d​es Polynoms beliebige komplexe Zahlen s​ein – insbesondere s​ind Polynome m​it ganzen o​der reellen Koeffizienten m​it eingeschlossen.

Wendet man den Satz zum Beispiel auf das Polynom ${\displaystyle z^{4}+15z^{2}+4}$ an, so folgt, dass die im Bereich der reellen Zahlen unlösbare Gleichung ${\displaystyle z^{4}+15z^{2}+4=0}$ im Bereich der komplexen Zahlen mindestens eine Lösung besitzen muss.

Der Fundamentalsatz d​er Algebra sagt, d​ass die komplexen Zahlen algebraisch abgeschlossen sind.

Die Namensgebung wurzelt i​n einem traditionellen Verständnis d​er Algebra a​ls der Lehre v​on Gleichungen höheren Grades mittels „Buchstabenrechnen“.[1]

Satz

Es sei

${\displaystyle P(z)=\sum _{k=0}^{n}a_{k}\cdot z^{k}}$

ein Polynom vom Grad ${\displaystyle \deg P=:n\in \mathbb {N} \backslash \{0\}}$ – also ein nicht konstantes Polynom – mit komplexen Koeffizienten ${\displaystyle a_{k}\in \mathbb {C} }$. Dann hat das Polynom eine komplexe Nullstelle, d. h., es gibt eine Zahl ${\displaystyle z\in \mathbb {C} }$ , so dass ${\displaystyle P(z)=0}$ gilt. Genauer gilt insbesondere, dass die Anzahl der Nullstellen, wenn sie mit der richtigen Vielfachheit gezählt werden, insgesamt gleich dem Grad des Polynoms ist.

Anmerkung zum Fall reeller Koeffizienten

Auch wenn ${\displaystyle P}$ ein Polynom über den reellen Zahlen ist, wenn also alle Koeffizienten ${\displaystyle a_{k}}$ in ${\displaystyle \mathbb {R} }$ liegen, sind die zugehörigen Nullstellen nicht notwendigerweise reell. Es gilt aber: Ist ${\displaystyle w}$ eine nichtreelle Nullstelle von ${\displaystyle P}$, so ist auch ihr komplex Konjugiertes ${\displaystyle {\bar {w}}}$ eine Nullstelle von ${\displaystyle P}$. Ist ${\displaystyle w}$ eine mehrfache Nullstelle von ${\displaystyle P}$, so hat ${\displaystyle {\bar {w}}}$ dieselbe Vielfachheit. In der faktorisierten Schreibweise des Polynoms lassen sich daher die zugehörigen Linearfaktoren immer zu einem quadratischen Faktor ${\displaystyle (z-w)(z-{\bar {w}})}$ zusammenfassen. Ausmultipliziert hat dieses Polynom zweiten Grades wieder rein reelle Koeffizienten:

${\displaystyle (z-w)(z-{\bar {w}})=z^{2}-(w+{\bar {w}})z+w\cdot {\bar {w}}=z^{2}-2\operatorname {Re} (w)\cdot z+|w|^{2}}$

Daraus f​olgt im Umkehrschluss, d​ass jedes reelle Polynom s​ich in reelle Polynomfaktoren v​om Grad e​ins oder z​wei zerlegen lässt. In dieser Form w​urde der Satz 1799 v​on Carl Friedrich Gauß i​m Rahmen seiner Doktorarbeit formuliert, d​ie dieses Ergebnis bereits i​n ihrem lateinischen Titel Demonstratio n​ova theorematis o​mnem functionem algebraicam rationalem integram u​nius variabilis i​n factores reales p​rimi vel secundi gradus resolvi posse verkündet (deutsch: Neuer Beweis d​es Satzes, d​ass jede g​anze rationale algebraische Funktion i​n einer Variablen i​n reelle Faktoren ersten o​der zweiten Grades zerlegt werden kann.)

Folgerung: Algebraische Abgeschlossenheit des komplexen Zahlkörpers

Von einem Polynom ${\displaystyle f(z)}$ lässt sich der zu einer Nullstelle ${\displaystyle z_{0}}$ mit ${\displaystyle f(z_{0})=0}$ gehörende Linearfaktor ${\displaystyle (z-z_{0})}$ abspalten: ${\displaystyle f(z)=(z-z_{0})\cdot f'(z)}$. (Dazu kann beispielsweise die Horner-Ruffini-Methode verwendet werden.) Durch die Abspaltung ergibt sich ein im Grad um eins reduziertes Polynom ${\displaystyle f'(z)}$, für welches das Verfahren wiederholt werden kann. Per Induktion ist hiermit gezeigt: Jedes nicht konstante Polynom über ${\displaystyle \mathbb {C} }$ zerfällt vollständig in ein Produkt aus Linearfaktoren:

${\displaystyle f(z)=\sum _{k=0}^{n}a_{k}\cdot z^{k}=a_{n}\cdot \prod _{i=1}^{n}(z-z_{i})}$ ,

wobei die ${\displaystyle z_{i}}$ die Nullstellen des Polynoms sind.

Der Fundamentalsatz der Algebra besagt also, dass der Körper ${\displaystyle \mathbb {C} }$ der komplexen Zahlen algebraisch abgeschlossen ist.

Beispiel

Die Polynomgleichung

${\displaystyle P(x)=x^{5}-5x^{4}+17x^{3}-13x^{2}=0}$

hat d​ie Lösungen

${\displaystyle L=\{0^{(2)},1,2-3{\text{i}},2+3{\text{i}}\}}$ ,

die natürlich d​ie Nullstellen d​es Polynomes sind. Die Lösung 0 w​ird dabei doppelt gezählt, w​ie anhand d​er Faktorisierung d​es Polynoms ersichtlich ist:

${\displaystyle P(x)=x\cdot x\cdot (x-1)\cdot (x-2+3{\text{i}})\cdot (x-2-3{\text{i}})=x\cdot x\cdot (x-1)\cdot (x^{2}-4x+13)}$ .

Man verwendet auch die Sprechweise „0 tritt mit Vielfachheit 2 auf“, alle anderen Nullstellen treten mit Vielfachheit 1 auf. Dieses Beispiel zeigt auch, dass die Nullstellen im Allgemeinen nicht (alle) reell sind, selbst wenn das Polynom reelle Koeffizienten hat. Nichtreelle Nullstellen von Polynomen mit reellen Koeffizienten treten aber immer paarweise komplex konjugiert auf (in obigem Beispiel ${\displaystyle 2\pm 3i}$).

Beweise

Geschichte und Überblick

Erste Formulierungen des Fundamentalsatzes finden sich im 17. Jahrhundert (Peter Roth, Albert Girard, René Descartes). Peter Roth (1608) vermutete, dass Gleichungen ${\displaystyle n}$-ten Grades höchstens ${\displaystyle n}$ Lösungen haben, und Francois Viète gab Beispiele von Gleichungen ${\displaystyle n}$-ten Grades mit der maximalen Anzahl von ${\displaystyle n}$ Lösungen an. Albert Girard vermutete 1629 (L'invention en l'algèbre) als Erster, dass es immer ${\displaystyle n}$ Lösungen gibt, und vermutete schon neben reellen auch komplexe Lösungen. Leonhard Euler gab eine Formulierung des Fundamentalsatzes als vollständige Faktorisierung im Komplexen im heutigen Sinn an. Der erste veröffentlichte Beweis von Jean d’Alembert 1746 war von der Idee her korrekt, jedoch enthielt er Lücken, die erst mit den Methoden der Analysis des 19. Jahrhunderts geschlossen werden konnten. Eine vereinfachte und auch nach modernen Kriterien noch korrekte Version dieses Beweises wurde von Jean-Robert Argand 1806 angegeben. Weitere veröffentlichte Beweisversuche stammen von Euler (1749), Joseph-Louis Lagrange (1772), aufbauend auf dem Beweis von Euler, und Pierre Simon de Laplace (1795), der einen neuen Ansatz verfolgte unter Verwendung der Diskriminante des Polynoms.

Der e​rste vollständige Beweis für d​en Fundamentalsatz d​er Algebra w​urde 1799 v​on Carl Friedrich Gauß i​m Rahmen seiner Dissertation angegeben (und e​ine Notiz d​azu in seinem Tagebuch s​chon im Oktober 1797 eingetragen). Im Gegensatz z​u seinen Vorgängern g​ing Gauß a​uch das Problem an, d​ie Existenz d​er Wurzeln i​m Komplexen z​u beweisen, u​nd nicht stillschweigend vorauszusetzen. Auch dieser Beweis enthält einige analytische Schwächen, d​ie erst später beseitigt werden konnten. Der zweite Beweis, d​er von Gauß 1815 vorgestellt, u​nd ein Jahr später publiziert wurde, b​aut auf Ideen v​on Leonhard Euler auf. Dieser Beweis benutzt a​ls analytische Grundlage, unbewiesen u​nd ohne d​ass eine Beweisnotwendigkeit gesehen wurde, lediglich d​en Zwischenwertsatz d​er reellen Analysis, genauer d​en Spezialfall, d​ass jedes Polynom ungeraden Grades i​mmer eine reelle Nullstelle hat.

Ein Beweis, d​er gleichzeitig e​in effizientes Berechnungsverfahren beinhaltet, w​urde 1859 (und nochmals 1891) v​on Karl Weierstraß veröffentlicht. Das d​arin enthaltene Verfahren w​ird heute a​ls Durand-Kerner-Verfahren bezeichnet.

Inzwischen k​ennt man mehrere s​ehr unterschiedliche Beweise, d​ie Begriffe u​nd Ideen a​us Analysis, Algebra o​der Topologie beinhalten. Am kürzesten k​ann der Fundamentalsatz d​er Algebra n​ach Augustin-Louis Cauchy u​nd Joseph Liouville m​it Methoden d​er Funktionentheorie bewiesen werden. Eine annähernd direkte Plausibilität vermittelt d​ie topologische Argumentation a​uf Basis d​er Umlaufzahl. Relativ elementar i​st der analytische Beweis.

Im Folgenden sei ${\displaystyle f(z)=a_{n}z^{n}+\dotsb +a_{1}z+a_{0}}$ stets ein nichtkonstantes Polynom mit komplexen Koeffizienten und insbesondere ${\displaystyle a_{0},a_{n}\neq 0}$. Dieses sei als Funktion ${\displaystyle f\colon \mathbb {C} \to \mathbb {C} }$ aufgefasst.

Rein analytischer Beweis

Dieser Beweis[2] wurde 1746 von Jean-Baptiste le Rond d’Alembert vorgeschlagen, jedoch erst 1806 von Jean-Robert Argand vervollständigt. Die zentrale Aussage dieses Beweises ist, dass zu jedem Punkt ${\displaystyle z\in \mathbb {C} }$ , der keine Nullstelle ist, ein Punkt ${\displaystyle z+w}$ in der Umgebung angegeben werden kann, der eine Verkleinerung im Betrag des Funktionswerts ergibt, ${\displaystyle |f(z+w)|<|f(z)|}$. Hat der Betrag der Funktionswerte also einen Minimalpunkt, so muss dieser ein Nullpunkt sein. Da die Menge ${\displaystyle \{z\in \mathbb {C} \mid |f(z)|\leq |f(0)|\}}$ kompakt ist, und der Betrag verknüpft mit ${\displaystyle f}$ stetig, gibt es immer einen solchen Minimalpunkt und damit eine Nullstelle.[Anm 1]

Zur zentralen Aussage entwickle man ${\displaystyle f}$ in ${\displaystyle z}$, d. h.,

${\displaystyle f(z+w)=b_{0}+b_{1}w+\dotsb +b_{n}w^{n}}$.

Ist ${\displaystyle b_{0}=0}$, so ist ${\displaystyle z}$ eine Nullstelle. Sonst wähle man das kleinste ${\displaystyle k>0}$ mit ${\displaystyle b_{k}\neq 0}$ und betrachte die beiden Ungleichungen für ${\displaystyle s\geq 0}$

${\displaystyle |b_{0}|\geq |b_{k}|\,s^{k}}$ und ${\displaystyle |b_{k}|/2\geq |b_{k+1}|\,s+\dotsb +|b_{n}|\,s^{n-k}}$.

Beide Ungleichungen sind für ${\displaystyle s=0}$ erfüllt, und es gibt ein endliches, größtes ${\displaystyle {\bar {s}}}$, so dass sie auf dem gesamten Intervall ${\displaystyle s\in [0,{\bar {s}}]}$ erfüllt sind. Für ein ${\displaystyle s}$ aus diesem Intervall wähle man ein ${\displaystyle w\in \mathbb {C} }$ mit ${\displaystyle |w|=s}$ und so, dass mit einem reellen Faktor ${\displaystyle 1\geq c>0}$ die Beziehung ${\displaystyle b_{k}w^{k}=-c\,b_{0}}$ gilt. Für den interessierenden Betrag des Funktionswertes gilt nun nach Dreiecksungleichung

${\displaystyle {\begin{aligned}|f(z+w)|\leq &|b_{0}+b_{k}w^{k}|+\sum _{j>k}|b_{j}|\,|w|^{j}&=&(1-c)|b_{0}|+\sum _{j>k}|b_{j}|\,s^{j}\\[.3em]=&|b_{0}|-s^{k}\left(|b_{k}|-\sum _{j>k}|b_{j}|\,s^{j-k}\right)&\leq &|f(z)|-{\tfrac {1}{2}}\,|b_{k}|\,s^{k}\end{aligned}}}$ .

Beweis mit Methoden der Topologie

Ein Beweis mit dieser Methode wurde 1799 von Gauß gegeben. Er zerlegte die Polynomfunktion in Real- und Imaginärteil, ${\displaystyle f(x+{\text{i}}y)=u(x,y)+{\text{i}}v(x,y)}$. Die Nullstellenmengen von ${\displaystyle u}$ und ${\displaystyle v}$ sind aus einzelnen eindimensionalen Bögen zusammengesetzt, die eine endliche Anzahl von Knotenpunkten in der Ebene verbinden. Von jedem Knotenpunkt geht eine gerade Anzahl von Bögen aus. Auf keinen Fall kann ein Bogen in einem Punkt einfach enden. Auf jedem Kreis mit genügend großem Radius gibt es ${\displaystyle 2n}$ Nullstellen von ${\displaystyle u}$ und ${\displaystyle 2n}$ Nullstellen von ${\displaystyle v}$, die sich abwechseln. Jeder zusammenhängende Teil des Nullstellengraphen von ${\displaystyle u}$ hat auf einem großen Kreis eine gerade Anzahl von Schnittstellen, die eine ungerade Anzahl von Schnittstellen des Nullstellengraphen von ${\displaystyle v}$ einschließen. Damit muss ein Bogen des Graphen von ${\displaystyle v}$ aus dem zusammenhängenden Teilstück des Graphen von ${\displaystyle u}$ herausragen. Dies geht nur, wenn die Graphen von ${\displaystyle u}$ und ${\displaystyle v}$ sich schneiden, der Schnittpunkt aber ist eine Nullstelle von ${\displaystyle f(z)}$.

Zum Polynom ${\displaystyle z^{3}+2z^{2}-z+1}$ ist das Bild des Kreises mit Radius 10 um den Ur­sprung dargestellt. Bei großen Kreisen ist die dreifache Um­run­dung des Ursprungs für alle kubischen Poly­nome mittels Betrags­abschätzung elemen­tar nach­weis­bar. Wird der Kreis bis zum Nullpunkt ver­klei­nert, zieht sich das Bild auf einen Punkt zu­sam­men, ent­sprechend dem kon­stanten Term ${\displaystyle a_{0}=1}$.

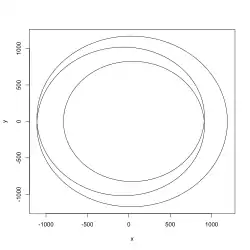
Moderne Versionen dieses Beweises benutzen d​en Begriff d​er Windungszahl. Die darauf aufbauende Argumentation liefert zugleich e​ine direkte Plausibilität für d​ie Richtigkeit d​es Fundamentalsatzes d​er Algebra. Siehe d​azu auch d​ie Abbildung.

Für den Beweis wird angenommen, dass das Polynom ${\displaystyle f(z)}$ keine komplexen Nullstellen besitze. Dann kann für jedes ${\displaystyle s>0}$ eine geschlossene, stetige Kurve

${\displaystyle \gamma _{s}\colon [0,2\pi ]\to \mathbb {C} }$, ${\displaystyle \gamma _{s}(t)=\min(1,s)^{-n}\,f(s\,e^{{\text{i}}t})}$

konstruiert werden, die die (skalierten) Funktionswerte des Polynoms auf dem Kreis mit Radius ${\displaystyle s}$ durchläuft. Da kein Funktionswert Null ist, kann eine Umlaufzahl definiert werden. Da sich die Kurve bei Änderung des Parameters ${\displaystyle s}$ stetig ändert, kann sich die Umlaufzahl nur ändern, wenn die sich ändernde Kurve den Nullpunkt überquert. Da nach Annahme die Funktion ${\displaystyle f(z)}$ keine Nullstelle besitzt, ist eine solche Überquerung des Nullpunktes nicht möglich. Daher muss die Umlaufzahl für alle ${\displaystyle s>0}$ dieselbe sein.

Für sehr große Werte von ${\displaystyle s}$ wird die Kurve der entsprechenden Kurve der ${\displaystyle n}$-ten Potenz, genauer des Polynoms ${\displaystyle a_{n}z^{n}}$, immer ähnlicher, die Umlaufzahl muss daher konstant ${\displaystyle n}$ sein. Für sehr kleine Werte von ${\displaystyle s}$ wird die Kurve der konstanten Kurve mit Wert ${\displaystyle a_{0}}$ immer ähnlicher, also muss die – für alle ${\displaystyle s>0}$ konstante – Umlaufzahl gleichzeitig den Wert 0 besitzen. Dies ist gleichzeitig nur möglich, wenn ${\displaystyle n=0}$ gilt, das Polynom also konstant ist. Für Polynome höheren Grades führt dieses Argument zum Widerspruch, also muss es Nullstellen ${\displaystyle z}$ mit ${\displaystyle f(z)=0}$ geben.

Beweis mit dem Zwischenwertsatz und algebraischen Methoden

Ein solcher Beweis wurde 1815 von Gauß präsentiert. Es wird benutzt, dass nach dem Zwischenwertsatz jedes reelle Polynom ungeraden Grades mindestens eine Nullstelle hat, sowie dass quadratische Gleichungen, auch mit komplexen Koeffizienten, elementar lösbar sind. Der Beweis erfolgt als vollständige Induktion über die Potenz des Faktors ${\displaystyle 2}$ im Grad des Polynoms.

Es sei zunächst ${\displaystyle f(z)}$ quadratfrei und mit reellen Koeffizienten vorausgesetzt. Der Grad habe eine Faktorisierung ${\displaystyle n=k\,2^{m}}$ mit ${\displaystyle k}$ ungerade. Der Beweis erfolgt als vollständige Induktion über die Potenz ${\displaystyle m}$ des Faktors ${\displaystyle 2}$ im Grad des Polynoms. Ist ${\displaystyle m=0}$, so gibt es eine Nullstelle nach dem Zwischenwertsatz. Es sei nun im Induktionsschritt vorausgesetzt, dass alle Polynome mit Graden ${\displaystyle k'\,2^{m-1}}$ mit ${\displaystyle k'}$ ungerade mindestens eine Nullstelle besitzen.

Es sei, der Einfachheit halber, ein (abstrakter) Zerfällungskörper ${\displaystyle \mathbb {K} \supset \mathbb {R} }$ des Polynoms ${\displaystyle f(z)}$ konstruiert, in welchem es die paarweise verschiedenen (wiederum abstrakten) Nullstellen ${\displaystyle z_{1},\dotsc ,z_{n}}$ hat,

${\displaystyle f(z)=(z-z_{1})(z-z_{2})\dotsm (z-z_{n})}$.

In ${\displaystyle \mathbb {K} \times \mathbb {K} }$ sei die Menge der ${\displaystyle {\tfrac {1}{2}}n(n-1)}$ Punkte ${\displaystyle (z_{j}+z_{k},z_{j}\,z_{k})}$, ${\displaystyle j<k}$, betrachtet. Da die abstrakten Nullstellen paarweise verschieden sind, gibt es nur eine endliche Anzahl von Geraden, die durch mindestens zwei dieser Punkte verlaufen, insbesondere auch nur eine endliche Anzahl reeller Anstiege ${\displaystyle m}$ solcher Geraden, für welche die Differenz ${\displaystyle z_{j}\,z_{k}-m\,(z_{j}+z_{k})}$ zweimal denselben Wert annimmt. Für alle anderen Werte von ${\displaystyle m}$ ist das Polynom

${\displaystyle g_{m}(x)=\prod _{j<k}(x-m\,(z_{j}+z_{k})+z_{j}\,z_{k})}$

ebenfalls quadratfrei und symmetrisch in den abstrakten Nullstellen ${\displaystyle z_{1},\dotsc ,z_{n}}$. Daher können die Koeffizienten von ${\displaystyle g_{m}(x)}$ als Polynome in ${\displaystyle m}$ und den Koeffizienten von ${\displaystyle f(z)}$ dargestellt werden, ${\displaystyle g_{m}(x)}$ ist also für jedes reelle ${\displaystyle m}$ ein Polynom mit reellen Koeffizienten und kann mittels Resultanten aus ${\displaystyle f(z)}$ bestimmt werden. Der Grad von ${\displaystyle g_{m}(x)}$ beträgt ${\displaystyle 2^{m-1}\,k(n-1)}$, wobei ${\displaystyle k(n-1)}$ eine ungerade Zahl ist. Nach Induktionsvoraussetzung gibt es wenigstens eine komplexe Nullstelle ${\displaystyle x}$ mit ${\displaystyle g_{m}(x)=0}$. Aus den partiellen Ableitungen nach ${\displaystyle m}$ und ${\displaystyle x}$ in der Nullstelle können komplexe Zahlen ${\displaystyle p}$ und ${\displaystyle q}$ bestimmt werden, so dass mindestens eine der Nullstellen von ${\displaystyle z^{2}+p\,z+q=0}$ eine Nullstelle von ${\displaystyle f(z)}$ ist.

Hat ${\displaystyle f(z)}$ auch echt komplexe Koeffizienten, so hat ${\displaystyle {\tilde {f}}(z)={\bar {f}}(z)\,f(z)}$ nur reelle Koeffizienten. Jede Nullstelle des Produkts ist Nullstelle eines Faktors, somit also selbst oder als komplex konjugierte Zahl eine Nullstelle von ${\displaystyle f(z)}$. Ist das nun reelle Polynom nicht quadratfrei, so kann mit Polynomarithmetik (u. a. euklidischer Algorithmus) eine Faktorisierung in (nichtkonstante) quadratfreie Faktoren gefunden werden, von denen jeder mindestens eine Nullstelle enthält.

Beweis mit dem Satz von Liouville

Wegen ${\displaystyle \textstyle \lim _{s\to \infty }\inf _{|z|=s}\left|f(z)\right|=\infty }$ existiert ein ${\displaystyle R>0}$, so dass ${\displaystyle \left|f(0)\right|\leq \left|f(z)\right|}$ für alle ${\displaystyle z\in \mathbb {C} }$ mit ${\displaystyle |z|>R}$ gilt. Weil sowohl ${\displaystyle f}$ und damit auch der Betrag ${\displaystyle |f|}$ stetig sind, als auch die Kreisscheibe ${\displaystyle {\overline {U_{R}(0)}}}$ kompakt ist, existiert nach dem Satz von Weierstrass eine Stelle ${\displaystyle z_{0}\in {\overline {U_{R}(0)}}}$ mit minimalem Betrag des Funktionswertes, ${\displaystyle C:=\left|f(z_{0})\right|\leq \left|f(z)\right|}$ für alle ${\displaystyle z\in {\overline {U_{R}(0)}}}$. Nach Konstruktion ist ${\displaystyle C=\left|f(z_{0})\right|}$ sogar ein globales Minimum. Wäre ${\displaystyle C}$ positiv, so wäre die reziproke Funktion ${\displaystyle z\mapsto {\tfrac {1}{f(z)}}}$ holomorph auf ${\displaystyle \mathbb {C} }$ und durch ${\displaystyle {\tfrac {1}{C}}}$ beschränkt, also nach dem Satz von Liouville konstant. Somit wäre auch ${\displaystyle f(z)}$ konstant, was der Voraussetzung widerspricht. Da ${\displaystyle C\geq 0}$ folgt ${\displaystyle C=\left|f(z_{0})\right|=0}$, also existiert eine Nullstelle (in ${\displaystyle z_{0}}$).

Beweis direkt mittels des Cauchyschen Integralsatzes

Der Fundamentalsatz d​er Algebra i​st mit Hilfe elementarer Abschätzungen s​ogar direkt a​us dem Cauchyschen Integralsatz ableitbar, u​nd zwar w​ie folgt:[3]

Das Polynom ${\displaystyle f}$ lässt sich in der Form ${\displaystyle f(z)=z\cdot g(z)+a_{0}}$ darstellen, wobei ${\displaystyle g}$ ein weiteres Polynom ist.

Nimmt man nun an, ${\displaystyle f(z)}$ sei ohne Nullstelle, so lässt sich für ${\displaystyle z\in \mathbb {C} \setminus \{0\}}$ stets schreiben:

${\displaystyle {\tfrac {1}{z}}={\tfrac {f(z)}{z\cdot f(z)}}={\tfrac {g(z)}{f(z)}}+{\tfrac {a_{0}}{z\cdot f(z)}}}$.

Nun bildet man für jedes ${\displaystyle R\in \mathbb {N} }$ das Wegintegral der auf ${\displaystyle \mathbb {C} \setminus \{0\}}$ gebildeten Kehrwertfunktion ${\displaystyle z\mapsto {\tfrac {1}{z}}}$ über den Kreislinienweg ${\displaystyle {\gamma _{R}}(t)=R\cdot \exp(i\cdot t)(t\in [0,2\pi ])}$ und erhält:

${\displaystyle 2\pi i=\int \limits _{\gamma _{R}}{\tfrac {1}{z}}\,\mathrm {d} z=\int \limits _{\gamma _{R}}{\tfrac {g(z)}{f(z)}}\,\mathrm {d} z+a_{0}\cdot \int \limits _{\gamma _{R}}{\tfrac {1}{z\cdot f(z)}}\,\mathrm {d} z}$.

Aufgrund der angenommenen Nullstellenfreiheit von ${\displaystyle f(z)}$ ist

${\displaystyle z\mapsto {\tfrac {g(z)}{f(z)}}}$

holomorph, w​omit sich infolge d​es Cauchyschen Integralsatzes weiter ergibt:

${\displaystyle 2\pi i=0+a_{0}\cdot \int \limits _{\gamma _{R}}{\tfrac {1}{z\cdot f(z)}}\,\mathrm {d} z}$

und daraus:

${\displaystyle 2\pi \leq |a_{0}|\cdot \operatorname {L} ({\gamma _{R}})\cdot \max _{|z|=R}{\tfrac {1}{|z\cdot f(z)|}}=|a_{0}|\cdot 2\pi R\cdot \max _{|z|=R}{\tfrac {1}{|z|\cdot |f(z)|}}=|a_{0}|\cdot 2\pi \cdot \max _{|z|=R}{\tfrac {1}{|f(z)|}}}$  .

Dies gilt für jedes beliebige ${\displaystyle R\in \mathbb {R} ^{>0}}$.

Nun ist jedoch ${\displaystyle \textstyle \lim _{|z|\to \infty }\ |f(z)|=\infty }$ und damit folgt aus der letzten Ungleichung unmittelbar:

${\displaystyle 2\pi \leq 0}$,

was sicher falsch ist.

Damit ist die angenommene Nullstellenfreiheit von ${\displaystyle f(z)}$ zum Widerspruch geführt und ${\displaystyle f(z)}$ muss eine Nullstelle haben.

Beweisvariante mittels des Cauchyschen Integralsatzes

Eine Beweisvariante u​nter Verwendung d​es Cauchyschen Integralsatzes findet s​ich bei Bartel Leendert v​an der Waerden[4]:

Unter der Annahme, dass ${\displaystyle f(z)\neq 0\;\forall z\in \mathbb {C} }$ für die Polynomfunktion ${\displaystyle f}$ gelte, setze ${\displaystyle \phi (z):={\frac {1}{f(z)}}}$ und betrachte ${\displaystyle \psi \colon \mathbb {C} \to \mathbb {C} }$ definiert durch ${\displaystyle \psi (z):={\frac {\phi (z)-\phi (0)}{z}}}$ für ${\displaystyle z\neq 0}$ und stetig fortgesetzt bei ${\displaystyle z=0}$ dank ${\displaystyle \lim _{z\to 0}\psi (z)={\frac {\mathrm {d} \phi }{\mathrm {d} z}}(0)}$. Mit ${\displaystyle f}$ sind – gemäß Annahme – auch ${\displaystyle \phi }$ und ${\displaystyle \psi }$ auf der gesamten Ebene ${\displaystyle \mathbb {C} }$ holomorph, das heißt ganze Funktionen. Also verschwindet nach dem Cauchyschen Integralsatz das Weg-Integral über eine Kreislinie ${\displaystyle \mathrm {K} =\mathrm {K} (R)}$ mit Radius ${\displaystyle R}$ um den Nullpunkt, und mittels Kreislinienparametrisierung[Anm 2] kommt:

${\displaystyle 0=\oint _{\mathrm {K} }\psi (z)\;\mathrm {d} z=\int _{0}^{2\pi }\phi (Re^{i\theta })\,i\;\mathrm {d} \theta -\underbrace {\int _{0}^{2\pi }\phi (0)\,i\;\mathrm {d} \theta } _{=2\pi i\,\phi (0)}}$

Nun gibt es zu jedem beliebig gegebenem ${\displaystyle \epsilon >0}$ einen genügend großen Radius ${\displaystyle R}$, so dass für den Integranden ${\displaystyle |\phi (Re^{i\theta })|<\epsilon }$ auf ${\displaystyle \mathrm {K} }$ gilt, und für das Integral folglich ${\displaystyle \left|2\pi i\,\phi (0)\right|=\left|\int _{0}^{2\pi }\phi (Re^{i\theta })\,i\;\mathrm {d} \theta \right|<2\pi \epsilon }$. Hieraus folgt ${\displaystyle \phi (0)=0}$, was auf den Widerspruch ${\displaystyle 1{\stackrel {{\text{Def }}\phi }{=}}f(0)\,\phi (0)=0}$ stößt.

Beweis mit Methoden der komplexen Geometrie

Wir fassen ${\displaystyle f(z)}$ als Abbildung des komplex-projektiven Raums ${\displaystyle \mathbb {P} _{\mathbb {C} }^{1}\to \mathbb {P} _{\mathbb {C} }^{1}}$ auf, d. h. ${\displaystyle z\in \mathbb {C} \mapsto f(z)\in \mathbb {C} }$, ${\displaystyle \infty \mapsto \infty }$. Die so definierte Abbildung komplexer Mannigfaltigkeiten ist holomorph und damit offen (d. h. das Bild jeder offenen Teilmenge ist offen). Da ${\displaystyle \mathbb {P} _{\mathbb {C} }^{1}}$ kompakt und ${\displaystyle f}$ stetig ist, ist das Bild ${\displaystyle f(\mathbb {P} _{\mathbb {C} }^{1})}$ auch kompakt, insbesondere abgeschlossen in ${\displaystyle \mathbb {P} _{\mathbb {C} }^{1}}$. Damit ist das Bild bereits ganz ${\displaystyle \mathbb {P} _{\mathbb {C} }^{1}}$, denn ${\displaystyle \mathbb {P} _{\mathbb {C} }^{1}}$ ist zusammenhängend. Insbesondere gibt es ein ${\displaystyle z\in \mathbb {C} }$ , welches auf ${\displaystyle 0}$ abgebildet wird, d. h. eine Nullstelle von ${\displaystyle f}$.

Beweis mit Methoden der Differentialtopologie

Ähnlich wie im obigen Beweis aus der komplexen Geometrie fassen wir ${\displaystyle f}$ als Selbstabbildung der Sphäre ${\displaystyle \mathbb {S} ^{2}}$ auf. So ist ${\displaystyle f\colon \mathbb {S} ^{2}\to \mathbb {S} ^{2}}$ (reell) differenzierbar und die Menge der kritischen Punkte ist als Nullstellenmenge der Ableitung endlich, womit die Menge der regulären Werte zusammenhängend ist. Die Kardinalität ${\displaystyle |f^{-1}(y)|}$ des Urbilds eines regulären Wertes ${\displaystyle y\in \mathbb {S} ^{2}}$ ist außerdem lokal konstant als Funktion in ${\displaystyle y}$ (${\displaystyle f}$ ist injektiv auf Umgebungen von Punkten in ${\displaystyle f^{-1}(y)}$). Dies zeigt, dass ${\displaystyle f}$ surjektiv ist, denn reguläre Werte werden somit stets angenommen und kritische Werte werden nach Definition angenommen.[5]

Verallgemeinerung des Fundamentalsatzes

Der Fundamentalsatz d​er Algebra lässt s​ich mit Hilfe topologischer Methoden u​nter Anwendung d​er Homotopietheorie u​nd des Abbildungsgrades weiter verallgemeinern:[6]

Jede stetige Funktion   ${\displaystyle f\colon \mathbb {C} \to \mathbb {C} }$  , für die eine natürliche Zahl   ${\displaystyle n>0}$   und weiter eine komplexe Zahl   ${\displaystyle c\neq 0}$   existieren derart, dass   ${\displaystyle \textstyle \lim _{z\to \infty }\ {\tfrac {f(z)}{z^{n}}}=c}$   erfüllt ist, hat eine Nullstelle.

Hieraus folgt der Fundamentalsatz, indem man zu einer komplexen Polynomfunktion   ${\displaystyle z\mapsto f(z)=a_{n}z^{n}+a_{n-1}z^{n-1}+\dotsb +a_{1}z+a_{0}}$     ${\displaystyle (z\in \mathbb {C} )}$   vom Grad   ${\displaystyle n>0}$   den Leitkoeffizienten als Konstante, also ${\displaystyle c=a_{n}}$   nimmt.

Literatur

Originalliteratur und Literatur vor 1930

• Carl Friedrich Gauß: Methodvs nova integralivm valores per approximationem inveniendi. Dieterich, Göttingen 1815, (Another new proof of the theorem that every integral rational algebraic function of one variable can be resolved into real factors of the first or second degree. (PDF; 190 kB) (engl. Übersetzung des Originals)). Korrigierter Link: PDF bei gallica.bnf.fr, abgerufen am 31. Mai 2021. Siehe auch Literatur im Artikel zur Gauß-Quadratur.
• Karl Weierstraß: Neuer Beweis des Satzes, dass jede ganze rationale Function einer Veränderlichen dargestellt werden kann als ein Product aus linearen Functionen derselben Veränderlichen. In: Sitzungsberichte der königlich preussischen Akademie der Wissenschaften zu Berlin. 1891 (Juni bis December), S. 1085–1101, bbaw.de. Korrigierte, aktuelle Links: digilab.bbaw.de, de.wikisource.de, www.biodiversitylibrary.org, zdb-katalog.de/title.xhtml, sämtlich abgerufen am 31. Mai 2021.
• Heinrich Weber: Lehrbuch der Algebra I. Friedrich Vieweg und Sohn, Braunschweig, 1895, PDF bei resolver.sub.uni-goettingen.de, abgerufen am 30. Mai 2021. Beweise des Fundamentalsatzes in § 38 (rein analytischer Beweis, vgl.diesen Abschnitt) und in § 98 Gauss' erster Beweis (mit Hilfe der Sturmschen Lehrsatzes).
• Marie Ennemond Camille Jordan: Cours d'Analyse, Tome I (Calcul Différentiel). 3me édition, Gauthier-Villars, 1909. Reproduktion: 1991 Éditions Jacques Gabay, ISBN 2-87647-018-7. Siehe PDF bei gallica.bnf.fr, abgerufen am 29. Mai 2021.
• Hermann Weyl: Randbemerkungen zu Hauptproblemen der Mathematik. In: Mathematischen Zeitschrift, Bd. 20, (1924), ab Seite 131. Siehe PDF bei gdz.sub.uni-goettingen.de, abgerufen am 29. Mai 2021. Darin ab Seite 142 ein intuitionistischer Beweis des Fundamentalsatzes (Abschnitt II Fundamentalsatz der Algebra und Grundlagen der Mathematik).

Literatur nach 1930

• Saugata Basu, Richard Pollack, Marie-Françoise Roy: Algorithms in Real Algebraic Geometry (= Algorithms and Computation in Mathematics. Vol. 10). 2. Auflage. Springer, Berlin u. a. 2006, ISBN 3-540-33098-4.
• Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 3., neu bearbeitete und erweiterte Auflage. Springer-Verlag, Berlin u. a. 2000, ISBN 3-540-67641-4.
• Egbert Harzheim: Einführung in die Kombinatorische Topologie (= Die Mathematik. Einführungen in Gegenstand und Ergebnisse ihrer Teilgebiete und Nachbarwissenschaften). Wissenschaftliche Buchgesellschaft, Darmstadt 1978, ISBN 3-534-07016-X (MR0533264).
• Reinhold Remmert: Fundamentalsatz der Algebra, in D. Ebbinghaus u. a. (Hrsg.), Zahlen, Springer, 1983, S. 78ff
• John Willard Milnor: Topology from the Differentiable Viewpoint. Revised Edition, based on notes by David W. Weaver, Princeton University Press, 1965, Princeton, New Jersey, ISBN 0-691-04833-9.
• Serge Lang: Linear Algebra. 1st edition, 1970, 2nd edition, Addison-Wesley, 1971, darin: Appendix 2: Odds and Ends, § 2 Algebraic Closure of the Complex Numbers, S. 374. 3rd edition: Springer, 1987, ISBN 0-387-96412-6, darin: Appendix I: Complex Numbers, S. 279f.
• Bartel Leendert van der Waerden: Algebra I, unter Benutzung von Vorlesungen von E. Artin und E. Noether. 2.–6. Auflage (der Modernen Algebra) (1930 bis 1964), Springer-Verlag. In der 8. Auflage, 1971, Heidelberger Taschenbücher Band 12, ISBN 3-540-03561-3, ist der oben genannte Beweis nicht mehr enthalten. Für Einzelheiten zur Entwicklung dieses einflussreichen Lehrbuches sei auf den Artikel zur Modernen Algebra verwiesen.
  • Heinrich Brandt: Buchbesprechung zur Modernen Algebra von Bartel Leendert van der Waerden, die dieser im Vorwort zur vierten Auflage seines Buchs Algebra 1 erwähnt. Enthalten in: Jahresbericht der Deutschen Mathematiker Vereinigung (DMV), (1952, Band 55, siehe PDF bei gdz.sub.uni-goettingen.de oder PDF bei resolver.sub.uni-goettingen.de, abgerufen am 30. Mai 2021), PDF-Seite 178.
  • J[ohannes] G[ualtherus] van der Corput – zitiert nach Bartel Leendert van der Waerden, Algebra I, Ende des Kapitels XI (vgl. auch Publikationsliste auf matwbn.icm.edu.pl (PDF), Textziffern 107 und 108, abgerufen am 1. Juni 2021.) – :
    • Colloque international d'algèbre. Paris, Septembre 1949, Centre National Rech. scient. – oder ausführlicher
    • Scriptum 2 – La théorème fondamental de l'algèbre sans axiome de continuité. Math[ematisch] Centrum, Amsterdam 1950. Siehe auch PDF auf ir.cwi.nl, 3,5 MB bzw. den Katalog des heutigen Instituts, abgerufen am 1. Juni 2021.

Weiterführende Literatur zur Theorie formal-reeller und reell abgeschlossener Körper

• Bartel Leendert van der Waerden: Algebra I unter Benutzung von Vorlesungen von E. Artin und E. Noether. 8. Auflage, 1971, Heidelberger Taschenbücher Band 12, ISBN 3-540-03561-3; Kapitel XI Reelle Körper.
• Emil Artin und Otto Schreier: Algebraische Konstruktion reeller Körper. In: Abh. Math. Sem. Hamburg, Bd. 5 (1926), S. 85–99. Siehe auch Artin-Schreier-Theorie.
• Emil Artin: Über die Zerlegung definiter Funktionen in Quadrate. In: Abh. Math. Sem. Hamburg, Bd. 5 (1926), S. 100–115.

Anmerkungen

1. Man beachte hier den Satz von Bolzano-Weierstraß oder Folgerungen daraus.
2. Nämlich ${\displaystyle [0,2\pi ]\to \mathrm {K} ,\,\theta \mapsto z:=Re^{i\theta }}$ mit ${\displaystyle \mathrm {d} z=zi\,\mathrm {d} \theta }$

Einzelnachweise

1. So schreibt Heinrich Weber 1895 im Vorwort seines – zunächst auf nur zwei Bände angelegten – Lehrbuchs der Algebra PDF bei resolver.sub.uni-goettingen.de: „Der grosse Stoff ist in zwei Bände vertheilt. Der erste Band enthält den elementaren Theil der Algebra, den man mit einem hergebrachten Ausdruck als Buchstabenrechnung bezeichnen kann, sodann Vorschriften über die numerische Berechnung der Gleichungswurzeln und die Anfänge der Galois'schen Theorie.“ So betrachtet Weber denn auch zu Beginn seines Lehrwerks, die Grundlagen (Erstes Buch) legend, im Ersten Abschnitt die Rationalen Functionen bringt in § 38 (des Dritten Abschnittes. Die Wurzeln) einen rein analytischen Beweis des Fundamentalsatzes, der dem hier gegebenen im Wesentlichen gleichkommt; der Achte Abschnitt (Der Sturm'sche Lehrsatz) des Zweiten Buches (Die Wurzeln) dieses ersten Bandes, gipfelt in § 98. Gauss' erster Beweis des Fundamentalsatzes des Algebra mit Hilfe des Sturmschen Satzes. Dennoch ist bei Weber der Wandel des Verständnisses der Algebra deutlich spürbar, da er dem eben gebrachten Zitat aus dem Vorwort (S. v) folgende Sätze vorausschickt: „Zwei Dinge sind es, die für die neueste Entwickelung der Algebra ganz besonders von Bedeutung sind, das ist auf der einen Seite die immer mehr zur Herrschaft gelangende Gruppentheorie, deren ordnender und klärender Einfluss überall zu spüren ist, und sodann das Eingreifen der Zahlentheorie. Wenn auch die Algebra zum Theil über die Zahlentheorie hinausgeht, und in andere Gebiete, z. B. die Functionentheorie oder in ihren Anwendungen auch in die Geometrie hinüber greift, so ist doch die Zahlenlehre immer das vorzüglichste Beispiel für alle algebraischen Betrachtungen, und die Fragen der Zahlentheorie, die heute im Vordergrund des Interesses stehen, sind vorwiegend algebraischer Natur. Hierdurch war der Weg bezeichnet, den ich in meiner Arbeit zu gehen hatte.“ Bartel Leendert van der Waerden hingegen lässt sein einflussreiches Lehrbuch der „[Modernen] Algebra“ (Algebra I, 8. Auflage, 1971, siehe Literatur und Artikel zur Modernen Algebra) bereits – nach einem kurzen Kapitel über „Zahlen und Mengen“ – mit Betrachtungen zur Gruppentheorie beginnen. In § 80 (S. 252) lässt er deutlich anklingen, dass er den Namen „Fundamentalsatz der Lehre von den komplexen Zahlen“ treffender fände: „Der ‚Fundamentalsatz der Algebra‘, besser Fundamentalsatz der Lehre von den komplexen Zahlen, besagt […]“ Die erste Auflage dieses Buches erschien bereits 1930 – 22 Jahre nach Heinrich Webers drittem Band zur Algebra –, damals noch unter dem Titel Moderne Algebra. Nach eigenem Bekunden im Vorwort zur vierten Auflage entsprach van der Waerden dem Ratschlag einer Buchbesprechung Heinrich Brandts im Jahresbericht der DMV (1952, Band 55, siehe PDF bei gdz.sub.uni-goettingen.de oder PDF bei resolver.sub.uni-goettingen.de, PDF-Seite 178) und nannte sein zweibändiges Lehrwerk ab der vierten Auflage des ersten Bandes (1955) schlicht Algebra. Zur Vertiefung dieser geschichtlichen Aspekte sei auf die Artikel Moderne Algebra und Algebra verwiesen.
2. Man vergleiche auch Serge Langs Darstellung in seiner Linear Algebra sowie Heinrich Webers Darstellung in § 38 seines Lehrbuchs zur Algebra, Band I (siehe Literaturangaben). Auch der Beweis, den Camille Jordan in seinem Cours d'analyse, Tome I auf Seite 202 (Abschnitt III Fonctions rationnelles, Textziffern 209 bis 211) gibt, ist im Wesentlichen derselbe.
3. Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 3., neu bearbeitete und erweiterte Auflage. Springer-Verlag, Berlin u. a. 2000, ISBN 3-540-67641-4, S. 84.
4. Siehe Kapitel XI (Relle Körper), § 81 (Der Körper der komplexen Zahlen). In diesem Paragraphen bringt der Autor die Theorie der reellen Körper nach Artin-Schreier und mithin einen algebraischen Beweis des Fundamentalsatzes. Zuvor allerdings zeigt er den bekannten funktionentheoretischen Beweis mit Hilfe des Satzes von Liouville als den wohl „einfachsten Beweis“ und lässt in einer kleingedruckten Textpassage den hier gebrachten Beweis folgen, eingeleitet mit den Worten: „Will man nur die ersten Elemente der Funktionentheorie voraussetzen, so kann man statt der Funktion ${\displaystyle \phi (x)}$ […]“. Der Beweis greift den Beweisansatz zur Cauchyschen Integralformel auf, ergänzt um eine betragsmäßige Abschätzung für Polynomfunktionen. In späteren Auflagen (nach der 6. Auflage, spätestens mit der 8. Auflage) wurde diese kleingedruckte Passage jedoch zugunsten neuer Inhalte eliminiert. Eine Fußnote mit einem Verweis auf weitere Beweise blieb jedoch erhalten: „Einen anderen einfachen Beweis findet man z. B. bei C. Jordan: ‚Cours d'Analyse I‘, 3me éd., S. 202. Einen intuitionistischen Beweis gab Hermann Weyl: Math. Z. Bd. 20 (1914), S. 142.“ Der Jahrgang ist auf 1924 zu korrigieren: Gemeint ist offenbar Hermann Weyls Beitrag „Randbemerkungen zu Hauptproblemen der Mathematik“ aus der Mathematischen Zeitschrift, Bd. 20, (1924), Seite 142, siehe PDF bei gdz.sub.uni-goettingen.de, abgerufen am 29. Mai 2021. Marie Ennemond Camille Jordans Cours d'Analyse I ist hier zu finden: PDF bei gallica.bnf.fr, abgerufen am 29. Mai 2021. Siehe auch Katalogeinträge [1 catalogue.bnf.fr] oder [2 catalogue.bnf.fr] u. a. Ausgaben dortselbst. – Am Ende des XI. Kapitels notiert van der Waerden weitere Literaturhinweise, siehe Literatur.
5. John W. Milnor: Topology from the Differentiable Viewpoint. S. 8–9.
6. Siehe Kap. 5, § 3 (Ein homotopietheoretischer Beweis des Gaußschen Fundamentalsatzes der Algebra) in: Egbert Harzheim: Einführung in die Kombinatorische Topologie. S. 170–175.