Konstruktion mit Zirkel und Lineal
In der euklidischen Geometrie versteht man unter einer Konstruktion mit Zirkel und Lineal die Entwicklung der exakten zeichnerischen Darstellung einer Figur auf der Grundlage vorgegebener Größen, wobei in der Regel nur Zirkel und Lineal verwendet werden dürfen. Das Lineal hat keine Markierungen; man kann damit also nur Geraden zeichnen, aber keine Strecken abmessen.
In der Geometrie werden Zirkel und Lineal auch als euklidische Werkzeuge bezeichnet. Problemlösungen, die auf andere Hilfsmittel zurückgreifen, wurden von den Griechen der klassischen Periode (und auch später von den meisten Geometrietreibenden bis ins 20. Jahrhundert) als weniger zufriedenstellend betrachtet.
Euklidische Werkzeuge
Die Beschränkung auf die „euklidischen Werkzeuge“ leitete sich aus den Postulaten ab, die Euklid am Anfang seines Lehrbuches Die Elemente zusammengestellt hatte. Daraus ergeben sich als einzige zugelassene Anwendungen dieser Werkzeuge:
- das Ziehen einer Geraden mit unbeschränkter Länge durch zwei beliebig gegebene, voneinander verschiedene Punkte,
- das Ziehen eines Kreises, der einen beliebig gegebenen Punkt als Mittelpunkt hat und durch einen beliebig gegebenen anderen Punkt verläuft, und
- das Übertragen einer Strecke auf eine Gerade oder als Sehne auf eine Kreislinie.
Geschichte
In der Antike forderte man vorerst kollabierende Zirkel, also solche, die beim Hochheben vom Blatt zuschnappen. Später war auch der nicht-kollabierende Zirkel für Konstruktionen erlaubt – nicht zuletzt, weil mit Lineal und kollabierendem Zirkel dieselben Punkte konstruiert werden können wie mit Lineal und nicht-kollabierendem Zirkel.
Die Konstruktion nur mittels Zirkel und (unskaliertem) Lineal galt viele Jahrhunderte als die Krone mathematischer Logik. Sie galt aber lange als weitgehend ausgereizt. Die Entdeckung einer Konstruktionsmethode für das regelmäßige Siebzehneck am 30. März 1796 durch Carl Friedrich Gauß war die erste wesentliche Neuerung seit zweitausend Jahren.[1][2] Mit Hilfe der im 19. Jahrhundert entwickelten Galoistheorie über Nullstellen von Polynomen konnten auch Aussagen über konstruierbare Polygone und die Dreiteilung beliebiger Winkel gemacht werden.
Viele Mathematiker haben sich jahrelang an – wie man heute weiß, unlösbaren – Aufgaben wie der Quadratur des Kreises versucht. Innerhalb der letzten gut 100 Jahre wurde die euklidische Einschränkung jedoch mehr und mehr als unnötige Begrenzung der Möglichkeiten gesehen. Einige Kritiker sahen darin sogar eine sogenannte Denkblockade. Daher wurde das Spektrum der Werkzeuge erweitert. Eine allgemeine Teilung des Winkels kann mit Hilfe einer Schablone erfolgen, deren Kante eine archimedische Spirale bildet. In der zweiten Hälfte des 19. Jahrhunderts kam mit dem „Tomahawk“ ein Gerät zur allgemeinen Dreiteilung des Winkels auf.
Nach dem Satz von Mohr-Mascheroni (nach Georg Mohr und Lorenzo Mascheroni) können Konstruktionsaufgaben mit Zirkel und Lineal auch mit dem Zirkel allein ausgeführt werden und nach dem Satz von Poncelet-Steiner (nach Jean-Victor Poncelet, Jakob Steiner) auch mit dem Lineal und einem vorgegebenen Kreis.
Algebraische Operationen
Mit Zirkel und Lineal kann man mit graphisch vorgegebenen oder bereits konstruierten reellen Zahlen die folgenden elementaren algebraischen Operationen ausführen (das heißt, deren Ergebnis in der Darstellung auf der Zahlengerade konstruieren):
- die Addition zweier Zahlen (Konstruktion einer Summe),
- die Subtraktion zweier Zahlen (Konstruktion einer Differenz),
- die Multiplikation zweier Zahlen (Konstruktion eines Produktes),
- die Division einer Zahl durch eine von Null verschiedene Zahl (Konstruktion eines Quotienten),
- das Quadratwurzelziehen aus einer nichtnegativen Zahl (Konstruktion einer Quadratwurzel),
- das Quadrieren einer Zahl (Konstruktion eines Quadrats).
- die dritte Potenz einer Zahl (Konstruktion eines Würfels)
Alle Zahlen, die nicht durch Anwendung endlich vieler dieser elementaren Operationen erhalten werden können, können auch nicht mit Zirkel und Lineal konstruiert werden. Das sind sogar überabzählbar viele, nämlich (wenn die Zahlen 0 und 1 vorgegeben sind) alle transzendenten Zahlen wie etwa die Kreiszahl oder die Eulersche Zahl , aber auch jede algebraische Zahl, deren Grad keine Zweierpotenz ist, wie etwa die Zahl vom Grad 3 als Nullstelle des über irreduziblen Polynoms .
Zur Konstruktion des Produktes und des Quotienten wird der Strahlensatz verwendet und zur Konstruktion von Quadratwurzeln der Kathetensatz oder der Höhensatz (siehe Zeichnungen weiter unten).
Eine geometrische Struktur, die eigens dazu entwickelt wurde, die Möglichkeiten der Konstruktionen mit Zirkel und Lineal algebraisch darzustellen, bilden die euklidischen Ebenen (im Sinne der synthetischen Geometrie) über euklidischen Körpern.
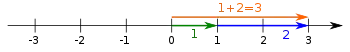
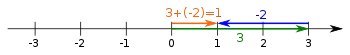

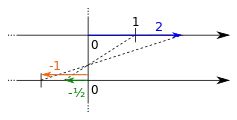 Multiplikation
Multiplikation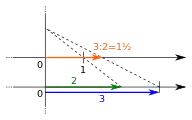
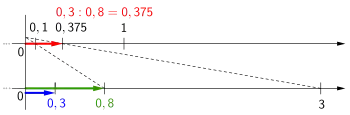 Division (Dividend um den Faktor 10 vergrößert)
Division (Dividend um den Faktor 10 vergrößert)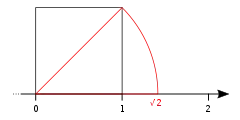 Konstruktion der Wurzel aus 2, Zwischenschritte – zum Beispiel, um das Quadrat zu konstruieren – wurden der Übersichtlichkeit wegen weggelassen.
Konstruktion der Wurzel aus 2, Zwischenschritte – zum Beispiel, um das Quadrat zu konstruieren – wurden der Übersichtlichkeit wegen weggelassen. Konstruktion der Wurzel aus 3
Konstruktion der Wurzel aus 3
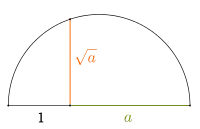 Konstruktion der Wurzel aus
Konstruktion der Wurzel aus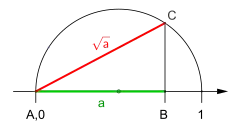 Konstruktion der Wurzel einer Zahl kleiner als 1
Konstruktion der Wurzel einer Zahl kleiner als 1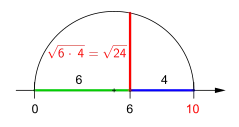 Konstruktion der Wurzel aus einem Produkt
Konstruktion der Wurzel aus einem Produkt
durch Addition der Faktoren (6 + 4) und mithilfe des Höhensatzes oder des geometrischen Mittels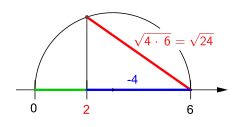 Konstruktion der Wurzel aus einem Produkt durch Subtraktion der Faktoren (6 − 4) und mithilfe des Kathetensatzes
Konstruktion der Wurzel aus einem Produkt durch Subtraktion der Faktoren (6 − 4) und mithilfe des Kathetensatzes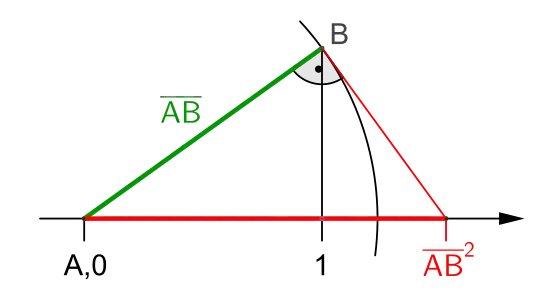 Quadrat einer Zahl größer als 1
Quadrat einer Zahl größer als 1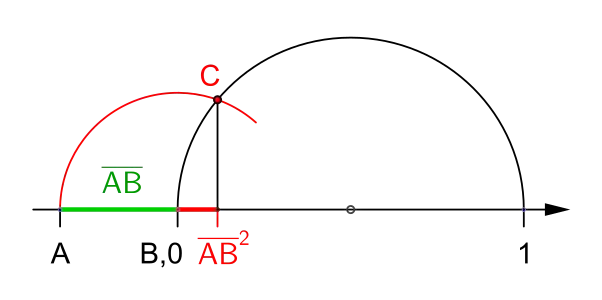 Quadrat einer Zahl kleiner als 1,
Quadrat einer Zahl kleiner als 1,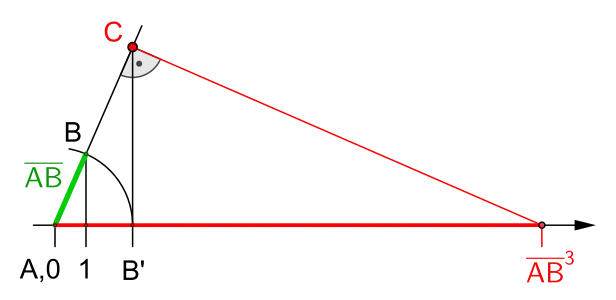 Dritte Potenz einer Zahl größer als 1
Dritte Potenz einer Zahl größer als 1
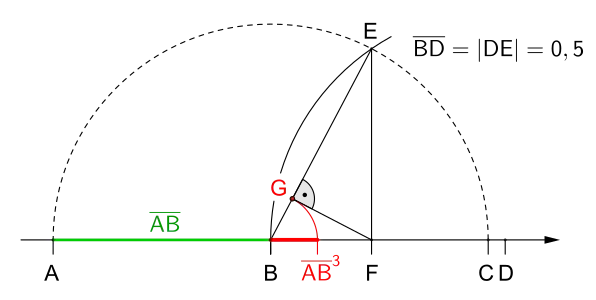 Dritte Potenz einer Zahl kleiner als 1, quasi die Weiterführung des Quadrierens einer Zahl kleiner als 1, denn
Dritte Potenz einer Zahl kleiner als 1, quasi die Weiterführung des Quadrierens einer Zahl kleiner als 1, denn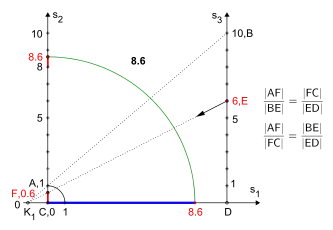 Konstruktion einer Dezimalzahl mithilfe des dritten Strahlensatzes
Konstruktion einer Dezimalzahl mithilfe des dritten Strahlensatzes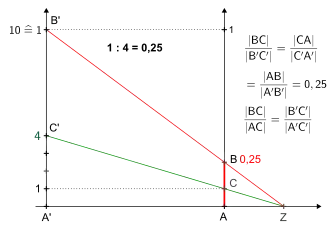 Konstruktion eines Quotienten mit als Dividenden (quasi um den Faktor 10 vergrößert) mithilfe des dritten Strahlensatzes.
Konstruktion eines Quotienten mit als Dividenden (quasi um den Faktor 10 vergrößert) mithilfe des dritten Strahlensatzes.
Die Strecke besteht aus zehn gleichen Abschnitten, der vierte Teilungspunkt entspricht dem Divisor .
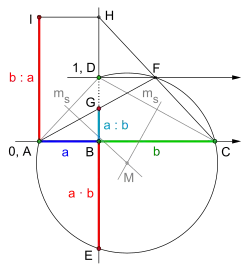 Konstruktion der Multiplikation und Division mit Kehrwert am Beispiel . = Mittelsenkrechte.
Konstruktion der Multiplikation und Division mit Kehrwert am Beispiel . = Mittelsenkrechte.
Die Reihenfolge der Konstruktionsschritte ist gleich der alphabetischen Reihenfolge der Punktebezeichnung.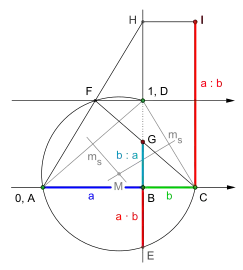 Konstruktion der Multiplikation und Division mit Kehrwert am Beispiel . = Mittelsenkrechte.
Konstruktion der Multiplikation und Division mit Kehrwert am Beispiel . = Mittelsenkrechte.
Die Reihenfolge der Konstruktionsschritte ist gleich der alphabetischen Reihenfolge der Punktebezeichnung.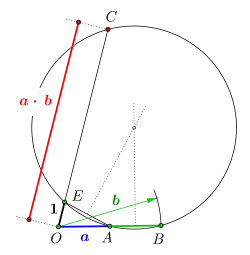 Konstruktion der Multiplikation mithilfe des Sekantensatzes. Den Mittelpunkt des Kreises bestimmen zwei Mittelsenkrechten.
Konstruktion der Multiplikation mithilfe des Sekantensatzes. Den Mittelpunkt des Kreises bestimmen zwei Mittelsenkrechten.
Die Reihenfolge der Konstruktionsschritte beginnt bei und setzt sich fort mit und
Unmögliche Konstruktionen
Viele geometrische Figuren können mit Zirkel und Lineal allein nicht exakt konstruiert werden. Darunter sind die klassischen Probleme der antiken Mathematik:
sowie
- die Kegelschnitte Ellipse (mit Ausnahme des Kreises), Parabel, Hyperbel,
- viele regelmäßige Vielecke und
- das Alhazensche Problem.
Der Beweis, dass diese Probleme grundsätzlich nicht mit Zirkel und Lineal zu lösen sind, gelang jedoch erst im 19. Jahrhundert. Dennoch bewirkten die Versuche, das Unmögliche zu vollbringen, eine Reihe von Leistungen. Die Griechen fanden einige Lösungen der „klassischen“ Probleme mit anderen Hilfsmitteln, wobei sie viele Resultate der höheren Geometrie entdeckten.
Näherungskonstruktion
Für einige Figuren, die mit Zirkel und Lineal nicht konstruiert werden können oder für die die Konstruktion zu aufwändig ist, gibt es Möglichkeiten, diese zumindest näherungsweise zu konstruieren. Diese Näherungskonstruktionen kommen dem wahren Objekt sehr nahe. Bekannte Näherungskonstruktionen sind zum Beispiel die Näherungskonstruktion für die Kreiszahl Pi von Kochański, die Näherungskonstruktionen für die Quadratur des Kreises, die Näherungskonstruktionen für das regelmäßige Siebeneck und die Näherungskonstruktionen für das regelmäßige Neuneck.
Anwendung
Die geometrischen Grundkonstruktionen spielen insbesondere in der Darstellenden Geometrie und im Technischen Zeichnen eine wesentliche Rolle. Ihre Vermittlung beginnt bereits mit der Schulmathematik und findet im Ausbildungsberuf des Technischen Zeichners vielfältige Anwendungen.
Literatur
- Ludwig Bieberbach: Theorie der Geometrischen Konstruktionen. Birkhäuser, Basel, 1952.
- Hans-Wolfgang Henn: Elementare Geometrie und Algebra: Basiswissen für Studium und Mathematikunterricht. Vieweg, 2003, S. 31–60.
- George E. Martin: Geometric Constructions. Springer, 2012, ISBN 978-1-461-20629-3.
- Nicholas D. Kazarinoff: Ruler and the Round: Classic Problems in Geometric Constructions. Courier Dover (Neuauflage), 2012, ISBN 978-0-486-14361-3.
Weblinks
Einzelnachweise
- Felix Klein: Gauß’ wissenschaftliches Tagebuch 1796–1814. In: Mathematische Annalen. Band 57, 1903, ISSN 0025-5831, S. 1–34 (digizeitschriften.de [abgerufen am 30. Oktober 2020]).
- Carl Friedrich Gauß: Disquisitiones arithmeticae. Humboldt-Universität zu Berlin, 1. Januar 1801 (hu-berlin.de [abgerufen am 30. Oktober 2020]).