Grundrechenart
Die Grundrechenarten (auch Grundrechnungsarten[1] oder schlicht Rechenarten[2] genannt) sind die vier mathematischen Operationen Addition, Subtraktion, Multiplikation und Division. Die Beherrschung der Grundrechenarten gehört zu den Grundfertigkeiten Lesen, Schreiben und Rechnen, die von Schülern während der Schulzeit zu erwerben sind.
Von den vier Grundrechenarten werden in der Arithmetik die Addition und die Multiplikation als Grundoperationen und die Subtraktion und die Division als abgeleitete Operationen angesehen. Für die beiden Grundoperationen gelten eine Reihe von Rechenregeln, wie die Kommutativgesetze, die Assoziativgesetze und die Distributivgesetze. In der Algebra werden diese Konzepte dann abstrahiert, um sie auf andere mathematische Objekte übertragen zu können.
Die vier Grundrechenarten
Addition
Die Addition ist der Vorgang des Zusammenzählens zweier (oder mehrerer) Zahlen. Der Operator für die Addition ist das Pluszeichen +, die Operanden werden Summanden genannt, der Term Summe und das Ergebnis heißt Summenwert / Wert der Summe:
- Summand + Summand = Summenwert
Das Ergebnis der Addition natürlicher Zahlen ist wieder eine natürliche Zahl. Durch Auswendiglernen und elementare Rechentechniken können kleine Zahlen im Kopf addiert werden. Die Addition großer Zahlen kann per Hand mit Hilfe der schriftlichen Addition durchgeführt werden.
Subtraktion
Die Subtraktion ist der Vorgang des Abziehens einer Zahl von einer anderen Zahl. Der Operator für die Subtraktion ist das Minuszeichen −, die beiden Operanden werden Minuend und Subtrahend genannt, der Term Differenz und das Ergebnis heißt Differenzwert / Wert der Differenz.
- Minuend − Subtrahend = Differenzwert
Das Ergebnis der Subtraktion zweier natürlicher Zahlen ist jedoch nur dann wieder eine natürliche Zahl, wenn der Minuend größer als der Subtrahend ist. Sind Minuend und Subtrahend gleich, erhält man als Ergebnis die Zahl Null, die oft auch zu den natürlichen Zahlen gezählt wird. Ist der Subtrahend größer als der Minuend, erhält man als Ergebnis eine negative Zahl. Um die Subtraktion uneingeschränkt durchführen zu können, wird daher der Zahlbereich auf die ganzen Zahlen erweitert. Die Subtraktion großer Zahlen kann per Hand mit Hilfe der schriftlichen Subtraktion durchgeführt werden.
Multiplikation
Die Multiplikation ist der Vorgang des Malnehmens zweier (oder mehrerer) Zahlen. Der Operator für die Multiplikation ist das Malzeichen · (oder ×), die Operanden werden Multiplikator und Multiplikand genannt, der Term Produkt und das Ergebnis heißt Produktwert / Wert des Produkts:
- Multiplikator · Multiplikand = Produktwert
Bedarf es keiner Unterscheidung von Multiplikator und Multiplikand, bezeichnet man beide oft zusammenfassend als Faktoren.
Sind die Faktoren natürliche oder ganze Zahlen, so ist das Ergebnis der Multiplikation ebenfalls wieder eine natürliche oder ganze Zahl. Durch Auswendiglernen des Einmaleins können kleine Zahlen im Kopf multipliziert werden. Die Multiplikation großer Zahlen kann per Hand mit Hilfe der schriftlichen Multiplikation durchgeführt werden.
Division
Die Division ist der Vorgang des Teilens einer Zahl durch eine andere Zahl. Der Operator für die Division ist das Geteiltzeichen : (oder /), die beiden Operanden werden Dividend und Divisor genannt, der Term Quotient und das Ergebnis heißt Quotientenwert / Wert des Quotienten:
- Dividend : Divisor = Quotientenwert
Das Ergebnis einer Division zweier natürlicher oder ganzer Zahlen ist jedoch nur dann wieder eine natürliche oder ganze Zahl, wenn der Dividend ein Vielfaches des Divisors ist. Andernfalls erhält man eine Bruchzahl. Um die Division uneingeschränkt durchführen zu können, wird daher der Zahlbereich auf die rationalen Zahlen erweitert. Die Division durch null kann jedoch nicht sinnvoll definiert werden. Die Division großer Zahlen kann per Hand mit Hilfe der schriftlichen Division durchgeführt werden.
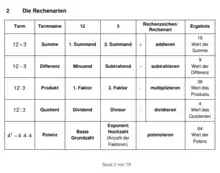
Grundrechenarten im Unterricht
Die Grundrechenarten werden während der ersten Schuljahre im Mathematikunterricht behandelt. In der Grundschule (Primarstufe) wird zunächst das Rechnen mit kleinen natürlichen Zahlen gelehrt und später auf größere Zahlen erweitert. Unterrichtsinhalte sind auch das kleine Einmaleins, die Division mit Rest, das Lösen einfacher Gleichungen und der Dreisatz. Es werden Kopfrechnen, schriftliches Rechnen, Überschlagsrechnen und Anwendungen in Form von Textaufgaben eingeübt. Für vorteilhaftes Rechnen werden einfache Rechengesetze angewendet. In den ersten Jahren einer weiterführenden Schule (Sekundarstufe I) werden dann auch negative Zahlen betrachtet, die Bruchrechnung und damit die rationalen Zahlen eingeführt, sowie die Gesetze bei der Verbindung der vier Grundrechenarten behandelt.[3]
Rechenregeln
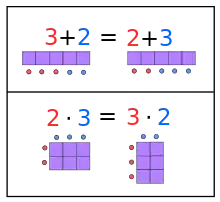
Im Folgenden sind , und Zahlen aus dem zugrundeliegenden Zahlbereich. Für die Addition und die Multiplikation gelten die Kommutativgesetze
- und ,
das heißt das Ergebnis einer Summe oder eines Produkts ist unabhängig von der Reihenfolge der Summanden bzw. Faktoren. Weiter gelten die Assoziativgesetze
- und .
Bei der Addition oder der Multiplikation mehrerer Zahlen ist es also unerheblich, in welcher Reihenfolge die Teilsummen oder Teilprodukte gebildet werden. Daher können bei Summen und Produkten die Klammern auch weggelassen werden. Zudem gelten die Distributivgesetze
- und ,
mit denen durch Ausmultiplizieren ein Produkt in eine Summe umgewandelt werden kann und umgekehrt durch Ausklammern eine Summe in ein Produkt. Weiterhin verhält sich die Zahl neutral bezüglich der Addition und die Zahl neutral bezüglich der Multiplikation, das heißt
- und .
Für die Subtraktion und die Division gelten diese Gesetze nicht oder nur eingeschränkt. Weitere Rechenregeln, wie Punkt vor Strich, die Klammerregeln und die Gesetze der Bruchrechnung, finden sich in der Formelsammlung Arithmetik.
Grundoperationen und abgeleitete Operationen
In der Arithmetik betrachtet man Addition und Multiplikation als Grundoperationen. Dabei wird die Addition natürlicher Zahlen als wiederholte Ermittlung des Nachfolgers eines Summanden und die Multiplikation natürlicher Zahlen als wiederholte Addition eines Faktors mit sich selbst angesehen. Diese Sichtweise wird dann auf andere Zahlbereiche, wie ganze oder rationale Zahlen, übertragen.
Subtraktion und Division führt man als abgeleitete mathematische Operationen der Grundoperationen ein. Zur Subtraktion und Division gelangt man über die Frage nach der Lösung elementarer Gleichungen der Form
- bzw. ,
wobei und gegebene Zahlen aus dem zugrundeliegenden Zahlbereich sind und die Zahl gesucht ist. Um diese Gleichungen zu lösen, wird eine Umkehroperation zur Addition benötigt, nämlich die Subtraktion, und ebenso eine Umkehroperation der Multiplikation, nämlich die Division:
- bzw. .
Die Subtraktion einer Zahl wird nun als Addition mit der Gegenzahl definiert und die Division durch eine Zahl als Multiplikation mit dem Kehrwert :
- bzw. .
Die Gegenzahl und der Kehrwert einer Zahl werden als die inversen Zahlen bezüglich der Addition und der Multiplikation bezeichnet. Auf diese Weise lassen sich die Rechenregeln für die Addition und Multiplikation auch auf die Subtraktion und Division übertragen.
Algebraische Strukturen
In der Algebra werden diese zunächst für die Arithmetik geschaffenen Konzepte abstrahiert, um sie auf andere mathematische Objekte übertragen zu können. Eine algebraische Struktur besteht dann aus einer Trägermenge (hier einer Zahlenmenge), sowie ein oder mehreren Verknüpfungen auf dieser Menge (hier die arithmetischen Operationen), die nicht aus ihr herausführen. Die verschiedenen algebraischen Strukturen unterscheiden sich dann nur über die Eigenschaften der Verknüpfungen (die Rechenregeln), die als Axiome festgelegt werden, nicht jedoch bezüglich der konkreten Elemente der Trägermenge. Für die Grundoperationen erhält man die folgenden algebraischen Strukturen:
- Die Menge der natürlichen Zahlen bildet mit der Addition eine kommutative Halbgruppe , in der für die Verknüpfung das Assoziativgesetz und das Kommutativgesetz gelten.
- Die Menge der natürlichen Zahlen bildet mit der Multiplikation ebenfalls eine kommutative Halbgruppe .
- Die Menge der ganzen Zahlen bildet mit der Addition eine kommutative Gruppe , in der zusätzlich ein neutrales Element existiert und zu jedem Element ein inverses Element.
- Die Menge der ganzen Zahlen bildet mit der Addition und der Multiplikation einen kommutativen Ring , in dem zusätzlich für die Verknüpfungen die Distributivgesetze gelten.
- Die Menge der rationalen Zahlen bildet mit der Addition und der Multiplikation einen Körper , in dem zusätzlich jedes Element außer der Null bezüglich der Multiplikation ein inverses Element besitzt.
Nach dem Permanenzprinzip gelten dabei alle Rechenregeln einer grundlegenden Struktur (hier eines einfachen Zahlbereichs mit den Grundoperationen) auch in einer entsprechend spezielleren Struktur (hier einem erweiterten Zahlbereich mit den gleichen Operationen). Diese Strukturierung und Axiomatisierung erlaubt es nun, gewonnene Erkenntnisse von Zahlen auf andere mathematische Objekte zu übertragen. Beispielsweise sind entsprechende Operationen bei Vektoren die Vektoraddition und bei Matrizen die Matrizenaddition. Spezielle Strukturen entstehen bei der Betrachtung endlicher Mengen, zum Beispiel Restklassenringe als mathematische Abstraktion einer Division mit Rest.
Geschichte
Alle vier Grundrechenarten waren bereits in der altägyptischen Mathematik und in der babylonischen Mathematik bekannt. Die Multiplikation und die Division waren jedoch keine eigenständigen arithmetischen Operationen. Die Multiplikation natürlicher Zahlen wurde auf das fortgesetzte Verdoppeln (Duplatio) eines Faktors und anschließende Addition der Teilergebnisse zurückgeführt. Die Division wurde bei nicht ganzzahligen Quotienten näherungsweise mittels fortgesetzter Halbierung (Mediatio) durchgeführt. Multiplikation und Division finden sich als eigenständige Operationen erst in der altgriechischen Mathematik, etwa bei Euklid und bei Pappos.[4]
Welche arithmetischen Operationen zu den Grundrechenarten gezählt werden, hat sich im Lauf der Zeit stark gewandelt. Bei Heron und Diophantos kamen zu den bekannten vier Rechenoperationen das Quadrieren und das Quadratwurzelziehen als weitere Grundrechenarten hinzu. In der indischen Mathematik wurden diese Operationen durch das allgemeinere Potenzieren und Wurzelziehen ersetzt und in neuerer Zeit um das Logarithmieren als siebte Grundrechenart ergänzt. In der islamischen Mathematik wurden beginnend mit Al-Chwarizmi auch die Duplatio und die Mediatio als eigene Rechenoperationen angesehen.[4]
In den Rechenbüchern des Mittelalters gab es weitere Ergänzungen der Grundrechenarten, die dort als „Spezies“ bezeichnet wurden. So finden sich um 1225 bei Johannes de Sacrobosco insgesamt neun dieser Spezies: Numeratio, Additio, Subtractio, Duplatio, Multiplicatio, Mediatio, Divisio, Progressio und Radicum extractio. Die Numeratio behandelte das Zählen, Lesen und Schreiben der Zahlen, als Progressio wurde die Summation aufeinanderfolgender natürlicher Zahlen bezeichnet und die Extractio umfasste lediglich das Ziehen von Quadratwurzeln. Erst 1494 verwarf Luca Pacioli die Duplatio und die Mediatio als Spezialfälle der Multiplikation und der Division wieder. Daraufhin erfolgten weitere Reduktionen bis Gemma Frisius 1540 als einer der ersten Autoren die Grundrechenarten auf die bekannten vier beschränkte.[4]
Literatur
- Walter Gellert (Hrsg.): Fachlexikon ABC Mathematik. Verlag Harri Deutsch, Thun und Frankfurt/Main 1978, ISBN 3-87144-336-0.
Weblinks
Einzelnachweise
- Grundrechnungsart. In: Duden Online-Wörterbuch. Bibliographisches Institut.
- Rechenart. In: PONS Online-Wörterbuch – Rechtschreibung und Fremdwörter. PONS.
- I.V.S. Mullis, M.O. Martin, C.A. Minnich, G.M. Stanco, A. Arora, V.A.S. Centurino, C.E. Castle (Hrsg.): TIMSS 2011 Encyclopedia: Education Policy and Curriculum in Mathematics and Science. Volumes 1 and 2. TIMSS & PIRLS International Study Center, Boston College, 2012, ISBN 978-1-889938-59-2 (timssandpirls.bc.edu).
- Johannes Tropfke: Geschichte der Elementar-Mathematik in systematischer Darstellung. Erster Band. Veit, Leipzig 1902, S. 29–31.