Tests der allgemeinen Relativitätstheorie

Tests der allgemeinen Relativitätstheorie werden zur Überprüfung des Standardmodells zur Beschreibung der Schwerkraft, der allgemeinen Relativitätstheorie (ART) Albert Einsteins, durchgeführt.

Zur Zeit ihrer Einführung im Jahre 1914 hatte die ART keine empirische Grundlage. Sie war ursprünglich vielmehr aus philosophischen Gründen sehr befriedigend, da sie das Äquivalenzprinzip erfüllte und das Newtonsche Gravitationsgesetz und die spezielle Relativitätstheorie als Grenzfälle enthielt[1]. In experimenteller Hinsicht war ab 1915 bekannt, dass sie die „anomale“ Perihelbewegung des Merkur erklären kann[2]. Zwar wurde schon 1919 nachgewiesen, dass Licht im Gravitationsfeld entsprechend der ART abgelenkt wird. Es dauerte allerdings bis 1959, bis es möglich war, die Voraussagen der ART im Bereich schwacher Gravitationsfelder zu testen, wodurch mögliche Abweichungen von der Theorie genau bestimmt werden konnten. Erst ab 1974 konnten mit dem Studium von Binärpulsaren sehr viel stärkere Gravitationsfelder erforscht werden, als es sie im Sonnensystem gibt. Schließlich erfolgte die Untersuchung von starken Gravitationsfeldern auch im Zusammenhang mit Schwarzen Löchern und Quasaren. Beobachtungen sind hier naturgemäß sehr schwierig, trotzdem stimmen die Ergebnisse mit den Voraussagen der ART bislang überein.

Gemäß dem Äquivalenzprinzip muss die in der speziellen Relativitätstheorie gültige Lorentzinvarianz lokal erfüllt sein („Lokale Lorentzinvarianz“). Für die entsprechenden Experimente siehe Tests der speziellen Relativitätstheorie.

Klassische Tests

Einstein schlug 1916 drei Tests der ART vor, die später als „die klassischen Tests der ART“ bezeichnet wurden:[3]

die Periheldrehung von Merkurs Orbit
die Ablenkung des Lichts im Gravitationsfeld der Sonne
die gravitative Rotverschiebung des Lichts.

Periheldrehung des Merkur

Die Periheldrehung der Bahn eines Planeten

In der newtonschen Physik beschreiben Objekte in einem Zweikörpersystem, also zwei sich umkreisende Himmelskörper, eine Ellipse mit dem Schwerpunkt als ihrem Brennpunkt. Der Punkt der größten Annäherung, das Perihel, ist an sich unbeweglich. Im Sonnensystem bewirkt jedoch eine Reihe von Effekten, dass das Perihel der Planeten um die Sonne rotiert. Die Hauptursache dafür ist die Anwesenheit anderer Planeten, die ihre Orbits gegenseitig stören. Ein anderer, sehr viel kleinerer Effekt, ist die Abplattung der Sonne. Ursprünglich wurden die Messungen der planetaren Orbits durch konventionelle Teleskope durchgeführt, jedoch erfolgen heute sehr viel genauere Messungen mit Radar.

Gemäß der newtonschen Gravitationstheorie wäre eine Periheldrehung von etwa 531" (Bogensekunden) pro Jahrhundert zu erwarten. 1859 erkannte Urbain Le Verrier, dass die Periheldrehung des Merkur von derjenigen, die aus den newtonschen Effekten folgt, abweicht. Seine Analyse der Transits des Merkur über der Sonnenscheibe von 1697 bis 1848 zeigte eine Abweichung gegenüber Newtons Theorie von etwa 38" pro tropischem Jahrhundert (später wurde dies auf 43" geändert).[4] Eine Reihe von Ad-hoc-Hypothesen und letztendlich falschen Lösungen wurde vorgeschlagen. In der ART hingegen wird die verbliebene Drehung, bzw. die Veränderung der Ausrichtung der orbitalen Ellipse in ihrer orbitalen Ebene, durch die Raumkrümmung verursacht. Einstein konnte zeigen, dass die ART sehr nahe in Übereinstimmung mit dem beobachteten Betrag von etwa 43" der Perihelverschiebung ist[2], was von beträchtlichem Gewicht für die Akzeptanz der ART war.

Die anderen Planeten sind ebenso Periheldrehungen unterworfen, jedoch haben sie geringere Orbitalgeschwindigkeiten und weniger exzentrische Orbits, deshalb sind ihre Verschiebungen kleiner und schwerer zu finden. Beispielsweise ist die Periheldrehung des Erdorbits aufgrund der ART etwa 5" pro Jahrhundert.[5] Die Perihelverschiebungen von Binärpulsar-Systemen wurden ebenso gemessen, wobei sie beispielsweise bei PSR J1915+1606 etwa 4,2° pro Jahr beträgt.[6] Diese Beobachtungen stimmen mit der ART überein.[7]

Ablenkung des Lichts durch die Sonne

Eine von Arthur Stanley Eddingtons Photographien der Sonnenfinsternis-Experimente von 1919, veröffentlicht 1920, als ihr Erfolg bekanntgegeben wurde.

Henry Cavendish (1784 in einem unveröffentlichten Manuskript) und Johann Georg von Soldner (1801) wiesen darauf hin, dass die newtonsche Gravitationstheorie eine Ablenkung von Sternenlicht um Himmelskörper voraussagt, sofern Licht als massebehaftetes Teilchen aufgefasst wird.[8] Annähernd derselbe Wert wie von Soldner wurde von Einstein aufgrund der Annahme des Äquivalenzprinzips alleine hergeleitet.[9] 1915 bemerkte er jedoch unter zusätzlicher Berücksichtigung der Raumzeitkrümmung in der ART, dass dies nur die Hälfte des korrekten Wertes ausmache.[10]

Die erste Beobachtung der Lichtablenkung wurde bei der Beobachtung der Positionsveränderung von Sternen gemacht, wenn diese auf der Himmelskugel sehr nahe der Sonne sind. Die Beobachtungen wurden durch Arthur Stanley Eddington und Frank Dyson während der totalen Sonnenfinsternis vom 29. Mai 1919 durchgeführt.[11] Das Resultat wurde als spektakuläre Nachricht aufgefasst und fand sich auf den Titelseiten vieler bedeutender Zeitungen wieder. Es machte Einstein und seine Theorie weltberühmt. Als er nach seiner Reaktion gefragt wurde, wenn die ART durch Eddington nicht bestätigt worden wäre, meinte Einstein spaßhaft: „Das hätte mir leid getan für den lieben Gott – die Theorie ist korrekt“.[12]

Die ursprüngliche Genauigkeit war zwar nicht sonderlich hoch, jedoch konnte eine moderne Re-Analyse der Daten zeigen, dass Eddingtons Analyse im Wesentlichen korrekt war.[13][14][15] Die Messung wurde durch ein Team des Lick-Observatoriums 1922 wiederholt, und ebenso 1973 von einem Team der University of Texas at Austin, mit Resultaten, die mit denen von 1919 übereinstimmten.[15] Eine wirklich große Präzision zeigten allerdings erst die Messungen mit Hilfe der Radioastronomie, beginnend in den 1960ern, die die letzten Zweifel an der Gültigkeit der ART-Werte ausräumen konnten.

Neben der Ablenkung durch die Sonne sind auch Einsteinringe ein Beispiel für die Lichtablenkung.

Gravitative Rotverschiebung des Lichts

Einstein sagte die gravitative Rotverschiebung des Lichts als Konsequenz des Äquivalenzprinzips bereits 1907 voraus,[16] jedoch erwies sich die Messung dieser Rotverschiebung als sehr schwierig. Obwohl sie durch Walter Sydney Adams bereits 1925 annähernd gemessen wurde, erfolgte eine klare Messung erst durch das Pound-Rebka-Experiment (1959). Dort wurde die relative Rotverschiebung von zwei Quellen, die sich an der Spitze und am Boden des Jefferson Turms der Harvard University befanden, durch Ausnutzung des Mößbauer-Effekts vermessen.[17][18] Das Resultat war in ausgezeichneter Übereinstimmung mit der ART und eine der ersten Präzisionsmessungen ihrer Voraussagen.

Moderne Tests

Die moderne Ära der Tests der allgemeinen Relativitätstheorie wurde zusätzlich durch Robert Henry Dicke und Leonard Schiff angetrieben, die ein Schema für Tests der ART entwickelten.[19][20][21] Sie betonten die Wichtigkeit nicht nur der klassischen Tests, sondern auch von Nullergebnissen, d. h. der Suche nach Effekten, die zwar prinzipiell in einer Gravitationstheorie auftreten können, jedoch nicht in der ART. Andere wichtige theoretische Entwicklungen betreffen die Berücksichtigung von Alternativen zur ART, besonders von Skalar-Tensor-Theorien wie der Brans-Dicke-Theorie[22] oder dem parametrisierten post-newtonschen Formalismus, einer Testtheorie, mit der Abweichungen von der ART wie auch Effekte im Zusammenhang mit dem Äquivalenzprinzip quantifiziert werden können.

Post-newtonsche Gravitationstests

Aufgrund des Fehlens von brauchbaren Alternativtheorien war der Bereich für Tests der ART ursprünglich eingeschränkt, denn es war nicht klar, welche Art von Tests sie von anderen Theorien unterscheidet. Damals war die ART die einzige relativistische Gravitationstheorie, die mit der speziellen Relativitätstheorie (in ihrem Gültigkeitsbereich) und den Beobachtungen übereinstimmte. Das änderte sich mit der Einführung der Brans-Dicke-Theorie 1960. Diese Theorie kann in gewissem Sinne als einfacher bezeichnet werden, da sie keine dimensionsbehafteten Konstanten enthält und verträglich ist mit dem Machschen Prinzip und Paul Diracs Large Number Hypothesis, also mit zwei philosophischen Ideen, die sich in der Geschichte der ART als einflussreich erwiesen haben. Dies führte schließlich zur Entwicklung des parametrisierten post-newtonschen Formalismus (PPN) durch Kenneth Nordtvedt und Clifford Will, der alle möglichen Abweichungen von Newtons Gravitationsgesetz für Größen erster Ordnung zu v / c (wobei v die Geschwindigkeit des Objekts und c die Lichtgeschwindigkeit ist) enthält. Diese Näherung erlaubt es, die möglichen Abweichungen von der ART für langsam bewegte Objekte in schwachen Gravitationsfeldern systematisch zu analysieren. Es wurden große experimentelle Anstrengungen unternommen, um die post-newtonschen Parameter einzugrenzen – mit dem Ergebnis, dass Abweichungen von der ART nur noch in sehr engen Grenzen möglich sind.[10]

Die Experimente zur Überprüfung der Gravitationslinseneffekte und Lichtverzögerungen grenzen denselben post-newtonschen Parameter, den sogenannten Eddington-Parameter γ, ein, der eine direkte Parametrisierung der Größe der Lichtablenkung durch eine Gravitationsquelle ist. Er ist gleich 1 für die ART, und nimmt verschiedene Werte in anderen Theorien an. Er ist der am besten bestimmte von den zehn post-newtonschen Parametern, jedoch auch für die Eingrenzung der anderen Parameter existieren Tests. Dazu zählen beispielsweise die Periheldrehung des Merkurs und die Tests des starken Äquivalenzprinzips.

Gravitationslinseneffekt

Gravitationslinse — Prinzipdarstellung

Der Gravitationslinseneffekt wurde bei entfernten astrophysikalischen Quellen beobachtet, doch ist es schwierig, die Bedingungen experimentell zu kontrollieren, und es ist ungewiss, wie die Ergebnisse im Rahmen der ART eingeordnet werden sollen. Die präzisesten Tests entsprechen Eddingtons Messungen aus dem Jahr 1919: Sie messen die Ablenkung der Strahlung einer entfernten Quelle durch die Sonne. Die Quellen, welche am genauesten analysiert werden können, sind entfernte Radioquellen, besonders Quasare. Die Richtungsgenauigkeit aller Teleskope ist grundsätzlich durch Diffraktion limitiert, und für Radioteleskope ist dies auch das praktische Limit. Eine wichtige Verbesserung, um Positionsdaten hoher Genauigkeit (im Bereich von Milli- bis Mikrobogensekunden) zu erhalten, wurde durch die Kombination von Radioteleskopen auf der ganzen Erde erreicht (VLBI). Mit dieser Technik werden durch Radiobeobachtungen die Phaseninformationen der mit Teleskopen gemessenen Radiosignale über weite Strecken miteinander verbunden. 2009 haben solche Teleskope die Ablenkungen der Radiowellen durch die Sonne mit extrem hoher Genauigkeit gemessen, wobei der Betrag der aus der ART folgenden Ablenkung auf 0,03 Prozent genau gemessen wurde.[23][24] Auf diesem Niveau müssen systematische Effekte sorgfältig berücksichtigt werden, um die genaue Position der Erdteleskope zu bestimmen. Einige wichtige Effekte sind Nutation, Rotation, atmosphärische Brechung, tektonische Verschiebung und Gezeitenwellen. Ein anderer Effekt ist die Brechung der Radiowellen durch die Sonnenkorona. Bei der Unterscheidung hilft, dass dieser Effekt ein charakteristisches Spektrum hat, während gravitative Ablenkungen unabhängig von der Wellenlänge sind. Folglich kann eine sorgfältige Analyse von Messungen bei verschiedenen Frequenzen diese Fehlerquelle reduzieren.

Der gesamte Himmel wird durch die gravitative Lichtablenkung (verursacht durch die Sonne) leicht verzerrt (ausgenommen in Gegenrichtung der Sonne). Dieser Effekt wurde durch Hipparcos, einen astrometrischen Satelliten der Europäischen Weltraumorganisation, beobachtet. Er vermaß die Position von etwa 100.000 Sternen. Während der gesamten Mission wurden 3,5 Millionen relative Positionen bestimmt, jede davon mit einer Genauigkeit von durchschnittlich 3 Millibogensekunden (der Genauigkeit für einen Stern der Größe 8 bis 9). Da die Gravitationsablenkung senkrecht zur Richtung Erde-Sonne bereits 4,07 Millibogensekunden ist, sind Korrekturen für praktisch alle Sterne nötig. Ohne systematische Effekte kann der Fehler von 3 Millibogensekunden einer einzelnen Beobachtung auf die Quadratwurzeln der Anzahl der Positionen reduziert werden, was zu einer Präzision von 0,0016 Millibogensekunden führt. Systematische Effekte begrenzen die Genauigkeit der Bestimmung der Größe des gesamten Effekts auf 0,3 Prozent.[25]

Tests zur Verzögerung der Lichtlaufzeit

Irwin I. Shapiro schlug einen Test vor, der innerhalb des Sonnensystems durchgeführt werden kann, und manchmal als der vierte „klassische“ Test der ART genannt wird. Er berechnete eine relativistische Zeitverzögerung (Shapiro-Verzögerung) für die Zweiwegzeit (Hin- und Rückreise) von Radarsignalen, die von anderen Planeten reflektiert werden.[26] Die bloße Krümmung des Weges eines Photons, das nahe an der Sonne vorbeigeht, ist zu klein, um einen beobachtbaren Verzögerungseffekt hervorzubringen (wenn die Zweiweg-Zeit mit der Zeit verglichen wird, die ein geradlinig bewegtes Photon benötigt), jedoch sagt die ART eine Verzögerung voraus, die kontinuierlich aufgrund der gravitativen Zeitdilatation größer wird, wenn das Photon nahe an der Sonne vorbeigeht. Die Beobachtung von Radarreflexionen von Merkur und Venus, unmittelbar bevor und nachdem sie von der Sonne verfinstert wurden, zeigt eine Übereinstimmung zur ART mit einer maximalen Abweichung von 5 %.[27] In jüngerer Zeit wurde mit dem Cassini-Satelliten ein ähnliches Experiment durchgeführt, dessen maximale Abweichung von der ART gar nur 0,002 % betrug.[28][29] Mit der VLBI wurden darüber hinaus geschwindigkeitsabhängige (gravitomagnetische) Korrekturen der Shapiro-Verzögerung im Feld des bewegten Jupiter[30] und Saturn[31] gemessen.

Das Äquivalenzprinzip

Das Äquivalenzprinzip besagt in seiner einfachsten Form, dass die Flugbahnen eines fallenden Körpers in einem Gravitationsfeld unabhängig sein sollen von seiner Masse und inneren Struktur, vorausgesetzt sie sind klein genug, um nicht von der Umgebung oder durch Gezeitenkräfte beeinflusst zu werden. Dieses Prinzip wurde mit großer Präzision bestätigt durch das Eötvös-Experiment mit einer Torsionswaage, wo nach unterschiedlichen Beschleunigungen verschiedener Massen gesucht wurde. Grenzen bezüglich dieses Effekts und der Existenz einer kompositionsabhängigen fünften Kraft bzw. einer gravitativen Yukawa-Wechselwirkung sind bereits sehr eng gefasst.

Das starke Äquivalenzprinzip besagt unter anderem, dass fallende Körper, die durch ihre Gravitationskräfte zusammengehalten werden, wie beispielsweise Sterne, Planeten oder Schwarze Löcher, denselben Flugbahnen in einem Gravitationsfeld unterworfen sind, vorausgesetzt, dass dieselben Bedingungen erfüllt sind. Dies wird als Nordtvedt-Effekt bezeichnet, und wurde am genauesten durch Lunar Laser Ranging bestätigt.[32][33] Seit 1969 wurde damit die Entfernung einiger Stationen auf der Erde bezüglich des Mondes gemessen, wobei eine zentimetergenaue Präzision erreicht wird.[34] Dadurch wurde eine starke Eingrenzung verschiedener post-newtonscher Parameter erreicht.

Ein anderer Teil des starken Äquivalenzprinzips ist die Bedingung, dass die newtonsche Gravitationskonstante in der Zeit unveränderlich ist, und überall im Universum denselben Wert hat. Es gibt viele unabhängige Messungen, die eine mögliche Abweichung davon einschränken,[34] aber eine der besten beruht auf Lunar Laser Ranging. Diese Messungen ergaben, dass die Gravitationskonstante – sollte sie entgegen gegenwärtiger Ansicht doch veränderlich sein – sich nicht um mehr als 10⁻¹¹ pro Jahr ändern kann.

Gravitative Rotverschiebung

Gravitative Rotverschiebung

Der erste der oben diskutierten klassischen Tests, die gravitative Rotverschiebung, ist eine einfache Konsequenz des Äquivalenzprinzips, und wurde von Einstein 1907 vorhergesagt. An und für sich ist es kein Test in der Form der post-Newtonschen Tests, da jegliche Theorie, die das Äquivalenzprinzip beinhaltet, diesen Effekt ebenfalls voraussagen muss. Trotzdem ist der Nachweis dieses Effekts eine bedeutende Stütze für die relativistische Gravitationsauffassung, da das Fehlen der gravitativen Rotverschiebung der Relativitätstheorie klar widersprochen hätte. Die erste Beobachtung dieses Effekts war die Messung der Spektralverschiebung des Weißen Zwergsterns Sirius B durch Adams (1925). Obwohl diese als auch spätere Messungen der Spektralverschiebung anderer Weißer Zwergsterne mit den Vorhersagen der ART übereinstimmten, könnte eingewendet werden, dass die Verschiebung möglicherweise andere Ursachen hat, weswegen eine experimentelle Bestätigung unter Benutzung von terrestrischen Quellen zu bevorzugen wäre.

Die experimentelle Bestätigung der gravitativen Rotverschiebung unter Benutzung irdischer Quellen dauerte mehrere Jahrzehnte, da der Effekt hier viel kleiner ist und daher sehr genaue Frequenzmessungen nötig sind. Er wurde zuerst 1960 mithilfe des Mößbauer-Effekts experimentell nachgewiesen. Durch diesen können Photonen von Gammastrahlung mit einer sehr engen Linienbreite erzeugt werden. Das von Robert Pound und Glen Rebka durchgeführte Experiment, das später von Pound und Snyder verbessert worden ist, wird als Pound-Rebka-Experiment bezeichnet. Die Frequenzverschiebung konnte mit einer Genauigkeit von 1 % vermessen werden. Die Blauverschiebung der fallenden Photonen kann berechnet werden, indem man annimmt, dass sie eine äquivalente Masse gemäß ihrer Frequenz E=hf (wobei h das Plancksche Wirkungsquantum ist) und E=mc² besitzen – ein Resultat der speziellen Relativitätstheorie. Solch einfache Herleitungen übergehen allerdings die Tatsache, dass in der ART vielmehr Uhrengangraten als Energien verglichen werden. Mit anderen Worten, die „höhere Energie“ des Photons, nachdem es gefallen ist, kann auch dem langsameren Gang der Uhren in tieferen Bereichen des Gravitationspotentials zugeschrieben werden. Um die ART vollständig zu bestätigen, ist es wichtig zu zeigen, dass die Ankunftsrate der Photonen größer ist als die Emissionsrate. Ein sehr genaues Rotverschiebungsexperiment wurde 1976 durchgeführt,[35] wobei eine Wasserstoff-Maser-Uhr in einer Rakete auf eine Höhe von 10.000 km gebracht wurde, und ihre Rate mit einer identischen Uhr auf der Erdoberfläche verglichen wurde. Die gravitative Rotverschiebung wurde damit bis auf 0,007 % genau gemessen.

Obwohl GPS nicht als Test von grundlegender Physik konstruiert wurde, muss beim Betrieb dieses Navigationssystems die gravitative Rotverschiebung berücksichtigt werden, wobei Physiker die Zeitdaten analysiert haben, um Aussagen verschiedener Theorien zu überprüfen. Als der erste Satellit gestartet wurde, ignorierten einige Ingenieure die Voraussage einer bemerkbaren gravitativen Zeitdilatation, sodass der Satellit ohne entsprechende Uhreneinstellung gestartet wurde. Die Uhren zeigten die erwartete Verschiebung gemäß Relativitätstheorie von 38 Mikrosekunden pro Tag. Die Abweichungsrate ist ausreichend, um die Funktionen des GPS substanziell innerhalb von Stunden zu beeinträchtigen, wenn sie nicht berücksichtigt wird.[36]

Andere Präzisionstests in diesem Zusammenhang wurden beispielsweise mit dem Satelliten Gravity Probe A (1976) durchgeführt, wobei gezeigt wurde, dass Gravitations- und Geschwindigkeitseffekte die Möglichkeit, die Gangraten von Uhren im Orbit zu synchronisieren, beeinflussen. Beim Hafele-Keating-Experiment (1971) als auch beim Maryland-Experiment wurden Atomuhren in Flugzeugen benutzt, wodurch ebenfalls die relativistischen Gravitations- und Geschwindigkeitseffekte bestätigt wurden.[37][38]

Durch die Benutzung von optischen Uhren konnte die Genauigkeit inzwischen derart gesteigert werden, dass die gravitative Zeitdilatation selbst bei Abständen von unter einem Meter gemessen werden konnte. Chou et al. (2010) benutzen dabei Al⁺ Ionen als Uhren. Während ein Ion in Ruhe war, wurde das andere um 33 cm angehoben. Die ermittelte Rotverschiebung entsprach einer Höhendifferenz von 37 ± 15 cm, was in sehr guter Übereinstimmung zur Theorie ist.[39]

In einer im Jahr 2022 publizierten Arbeit berichten die Autoren, dass sie die gravitative Rotverschiebung sogar bei einer Höhendifferenz im Millimetermaßstab nachweisen konnten.[40]

Lense-Thirring-Effekt

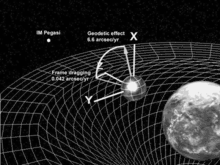
Wirkung des Frame-dragging-Effekts auf das Gyroskop

Gemäß dem Lense-Thirring-Effekt sollen sich kleine Präzessionen des Orbits eines Testpartikels ergeben, das sich um eine zentrale, rotierende Masse bewegt, beispielsweise einen Planeten oder einen Stern. Entsprechende Tests wurden mit den LAGEOS-Satelliten durchgeführt,[41] jedoch blieben einige Aspekte dieser Experimente umstritten.[42] Der Effekt könnte auch mit dem Mars Global Surveyor gemessen worden sein,[43] doch auch dies war nicht unumstritten.[44][45]

Der Gravity-Probe-B-Satellit, der 2004 gestartet wurde und bis 2005 in Funktion war, konnte diesen Effekt schließlich erstmals ohne Zweifel nachweisen. Bei diesem Experiment wurden vier mit einem Supraleiter beschichtete Quarzkugeln benutzt, die etwa so groß wie Tischtennisbälle waren.[46] Die Datenanalysen dauerten aufgrund des hohen Störungsniveaus und Schwierigkeiten in der korrekten Modellierung der Störungen bis 2011 an. Erst dann konnte ein sinnvolles Signal gefunden werden. Forscher an der Stanford University konnten am 4. Mai 2011 mitteilen, dass sie den Lense-Thirring-Effekt relativ zum entfernten Stern IM Pegasi gemessen haben. Der geodätische Effekt konnte dabei bis auf 0,2 Prozent genau nachgewiesen werden (Messwert: −6601,8 ± 18,3 Millibogensekunden/Jahr, ART-Wert: −6606,1 mas/Jahr) und der Lense-Thirring-Effekt wurde bis auf 37 Millibogensekunden mit einer Fehlermarge von 19 Prozent gemessen (Messwert: −37,2 ± 7,2 mas/Jahr, ART-Wert: −39,2 mas/Jahr). Zum Vergleich: Eine Millibogensekunde entspricht der Breite eines menschlichen Haares aus der Entfernung von 16 km.

Darüber hinaus werden Versuche durchgeführt, um den Lense-Thirring-Effekt der Sonne auf die Periheldrehungen der inneren Planeten nachzuweisen.[47] Eine weitere Konsequenz des Effekts wäre, dass die Orbitalebene der Sterne, die nahe einem supermassiven Schwarzen Loch kreisen, zur Präzession um die Drehachse des Schwarzen Lochs gebracht würde. Dieser Effekt sollte in den nächsten Jahren nachweisbar werden, und zwar durch astrometrische Beobachtung der Sterne im Zentrum der Milchstraße.[48] Durch einen Vergleich der Rate der orbitalen Präzession von zwei Sternen auf verschiedenen Umlaufbahnen sollte es zudem prinzipiell möglich sein, das „no-hair theorem“ der ART im Zusammenhang mit schwarzen Löchern zu bestätigen.[49]

Tests starker Felder

Pulsare sind schnell rotierende Neutronensterne, die während dieser Rotation konstant Radiopulse emittieren. Deswegen können sie auch als Uhren angesehen werden, was sehr genaue Überprüfungen ihrer orbitalen Bewegungen erlaubt. Beobachtungen von Pulsaren, die sich im Orbit um andere Sterne befinden, haben allesamt Periheldrehungen nachgewiesen, die nicht auf klassischem Wege erklärt werden können, sondern nur mit der ART. Beispielsweise hat der Hulse-Taylor Binärpulsar PSR J1915+1606 (ein Neutronensternpaar, wobei einer davon ein Pulsar ist) eine beobachtete Präzession von über 4° pro Jahr. Diese Präzession wurde benutzt, um die Masse der Komponenten zu errechnen.

Analog zur Emission elektromagnetischer Strahlung durch Atome und Moleküle kann eine Massenverteilung mit einem Quadrupol-Moment oder einer höheren Art von Vibration, oder wenn sie asymmetrisch und in Rotation ist, Gravitationswellen emittieren. Diese sollten sich mit Lichtgeschwindigkeit ausbreiten. So verlieren beispielsweise Planeten im Orbit um die Sonne Energie via Gravitationsstrahlung, allerdings ist dieser Effekt so klein, dass es unwahrscheinlich ist, dass er in nächster Zeit beobachtet werden kann (die Gravitationsstrahlung der Erde beläuft sich auf ca. 200 Watt). Durch den Hulse-Taylor-Pulsar konnte diese Strahlung indirekt nachgewiesen werden. Präzise Zeitmessungen der Pulsare zeigten, dass deren Orbits nur näherungsweise den Keplerschen Gesetzen entsprechen, denn mit der Zeit bewegen sie sich spiralförmig aufeinander zu, wodurch sie einen Energieverlust zeigen, der in enger Übereinstimmung mit der vorausgesagten Energieabgabe durch Gravitationswellen ist. Obwohl also die Wellen nicht direkt gemessen worden sind, ist die Berücksichtigung ihrer Auswirkung notwendig, um die Orbits zu erklären. Für diese Arbeit erhielten Hulse und Taylor den Nobelpreis.

Der 2003 entdeckte Doppelpulsar PSR J0737-3039 weist eine Periheldrehung von 16,90° pro Jahr auf; im Gegensatz zum Hulse-Taylor-Pulsar handelt es sich bei beiden Sternen um Pulsare, was Präzisionsmessungen beider Teile des Systems erlaubt. Aufgrund der Tatsache, dass das System fast direkt „an der Kante“ beobachtet werden kann (Inklination 90°), und der sehr geringen transversalen Geschwindigkeit des Systems aus Sicht der Erde, eignet sich J0737−3039 bislang mit Abstand am besten für Tests starker Gravitationsfelder der ART. Einige verschiedene Effekte wurden beobachtet, einschließlich der Abnahme des Orbits wie im Hulse-Taylor-System. Nachdem das System 2½ Jahre beobachtet wurde, waren vier unabhängige Tests der ART möglich, der genaueste (die Shapiro-Verzögerung) bestätigte die Voraussagen der ART innerhalb von 0,05 %.[50]

Experimente zum Nachweis Schwarzer Löcher sind indirekter Natur. Sie betreffen die Wirkungen ihrer außerordentlich starken Gravitationsfelder auf in der Nähe befindliche Sterne, die Entstehung von Akkretionsscheiben, die Ablenkung von Lichtstrahlen, die gravitative Zeitdilatation und Rotverschiebung sowie andere Effekte. Siehe für weitere Details: Beobachtungsmethoden von Schwarzen Löchern.

Gravitationswellen

Zweidimensionale Darstellung von Gravitationswellen zweier Neutronensterne

Eine Reihe von Gravitationswellendetektoren wurden errichtet, zur direkten Messung von Gravitationswellen, die von astronomischen Objekten abgestrahlt werden, wie beispielsweise beim Zusammenschluss von zwei Neutronensternen. Aktuell ist der genaueste Detektor das Laser Interferometer Gravitational-wave Observatory (LIGO), das seit 2002 operiert und mittlerweile zum Advanced LIGO-Detektor ausgebaut wurde. Dieser konnte im September 2015 die ersten Gravitationswellen direkt messen.[51] Zukünftige Detektoren mit deutlich verbesserter Präzision werden entwickelt oder sind in Planung, wie beispielsweise die geplante Mission Laser Interferometer Space Antenna (LISA) oder das Einstein-Teleskop. Es wird erwartet, dass Advanced-LIGO Gravitationswellen-Ereignisse möglicherweise jeden Tag beobachten kann.

Kosmologische Tests

Tests der ART im größtmöglichen, kosmologischen Maßstab sind nicht annähernd so zwingend wie beispielsweise Sonnensystem-Tests.[52] Der erste dieser Tests war die Voraussage und Entdeckung der Expansion des Universums. 1922 fand Alexander Alexandrowitsch Friedmann, dass die Gleichungen der ART nichtstationäre Lösungen beinhalten (selbst bei Anwesenheit einer kosmologischen Konstante). 1927 zeigte Georges Lemaître, dass statische Lösungen der Gleichungen der ART wie die ursprüngliche Lösung Einsteins, die bei Anwesenheit einer kosmologischen Konstante auftreten sollen, instabil sind und deshalb nicht existieren, d. h. das Universum muss entweder expandieren oder kontrahieren. Lemaître machte dabei die explizite Voraussage, dass das Universum expandiert. Er leitete auch eine Beziehung zwischen Rotverschiebung und Entfernung ab, die als Hubble-Gesetz bekannt wurde.[53][54] Die tatsächlich von Edwin Hubble (1929) entdeckte Rotverschiebung und damit zusammenhängend die Expansion des Universums, wurde von vielen (auch heute noch) als direkte Bestätigung der Vorhersagen der ART betrachtet.[55] Das führte dazu, dass auch Einstein 1931 mit den Lösungen von Friedmann und Lemaître übereinstimmte.[56] In den 1930ern, hauptsächlich durch die Arbeit von Edward Arthur Milne, wurde allerdings erkannt, dass die lineare Beziehung zwischen der Rotverschiebung und dem Abstand sich mehr aus der allgemeinen Annahme der Gleichförmigkeit und Isotropie herleitet als speziell aus der ART.[57] Trotzdem war die zum damaligen Zeitpunkt dramatische Vorhersage eines nichtstatischen Universums keineswegs trivial und hauptsächlich durch die ART motiviert.[58]

Einige andere kosmologische Tests sind die Suche nach Gravitationswellen, die während der kosmischen Inflation erzeugt wurden, welche in der Polarisation der kosmischen Hintergrundstrahlung oder mit dem geplanten weltraumbasierten Gravitationswelleninterferometer „Big Bang Observer“ (BBO) beobachtet werden könnten. Andere Tests bei hoher Rotverschiebung zielen darauf ab, die Möglichkeit alternativer Gravitationstheorien einzuschränken und die Variation der Gravitationskonstante seit der Primordialen Nukleosynthese zu überprüfen.

Einzelnachweise

Sekundärquellen

N. Ashby: Relativity in the Global Positioning System. In: Living Reviews in Relativity. Band 6, Nr. 1, 2003 (livingreviews.org [abgerufen am 23. Juni 2011]).

S. Chandrasekhar: The Role of General Relativity in Astronomy: Retrospect and Prospect. In: Journal of Astrophysics and Astronomy. Band 1, Nr. 1, 1980, S. 33–45, doi:10.1007/BF02727948 (ias.ac.in [PDF]).

L. Iorio (Hrsg.): The Measurement of Gravitomagnetism: A Challenging Enterprise. Hauppage (New York) 2007, ISBN 1-60021-002-3.

Helge Kragh, Robert W. Smith: Who discovered the expanding universe. In: History of Science. Band 41, 2003, S. 141–162, bibcode:2003HisSc..41..141K.

Charles W. Misner, Kip S. Thorne, John Archibald Wheeler: Gravitation. Hrsg.: Freeman. San Francisco 1973, ISBN 978-0-7167-0344-0.

W. Pauli: Relativitätstheorie. Hrsg.: Springer. Heidelberg 2000, ISBN 3-540-67312-1, Teil 4. Allgemeine Relativitätstheorie.

Slava G. Turyshev: Experimental Tests of General Relativity. In: Annual Review of Nuclear and Particle Systems. Band 58, Nr. 1, 2008, S. 207–248, arxiv:0806.1731.

C. M. Will: Theory and Experiment in Gravitational Physics. Hrsg.: University Press. Cambridge 1993, ISBN 0-521-43973-6.

C. M. Will: 100 years of relativity. In: A. Ashtekar (Hrsg.): World Scientific. Singapore 2005, ISBN 981-256-394-6, Was Einstein Right? Testing Relativity at the Centenary, S. 205–227, arxiv:gr-qc/0504086.

C. M. Will: The Confrontation between General Relativity and Experiment. In: Living Reviews in Relativity. Band 9, Nr. 3, 2006 (livingreviews.org [abgerufen am 23. Juni 2011]).

C. M. Will: Resource Letter PTG-1: Precision Tests of Gravity. In: American Journal of Physics. Band 78, Nr. 12, 2010, S. 1240–1247, arxiv:1008.0296.

Primärquellen

Albert Einstein: Die formale Grundlage der allgemeinen Relativitätstheorie. In: Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin. Band 46, 1914, S. 1030–1085 (archive.org).
Albert Einstein: Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie. In: Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin. Band 47, 1915, S. 831–839 (archive.org).
Albert Einstein: Die Grundlage der allgemeinen Relativitätstheorie. In: Annalen der Physik. Band 49, 1916, S. 769–782 (uni-augsburg.de [PDF]).
U. Le Verrier (1859), (in French), „Lettre de M. Le Verrier à M. Faye sur la théorie de Mercure et sur le mouvement du périhélie de cette planète“, Comptes rendus hebdomadaires des séances de l'Académie des sciences (Paris), vol. 49 (1859), S. 379–383.
Tai L. Chow,: Gravity, black holes, and the very early universe: an introduction to general relativity and cosmology. Hrsg.: Springer. 2008, ISBN 0-387-73629-8, S. 70.
Richard Alfred Matzner: Dictionary of geophysics, astrophysics, and astronomy. Hrsg.: CRC Press. 2001, ISBN 0-8493-2891-8, S. 356.
Weisberg et al.: The Relativistic Binary Pulsar B1913+16: Thirty Years of Observations and Analysis. In: Astronomical Society of the Pacific (Hrsg.): ASP Conference Series. 328 Binary Radio Pulsars.. San Francisco Juli 2005, S. 25, arxiv:astro-ph/0407149, bibcode:2005ASPC..328...25W (aspbooks.org).
Johann Georg von Soldner: Ueber die Ablenkung eines Lichtstrals von seiner geradlinigen Bewegung, durch die Attraktion eines Weltkörpers, an welchem er nahe vorbei geht. In: Astronomisches Jahrbuch für das Jahr 1804. 1804, S. 161–172.
Albert Einstein: Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes. In: Annalen der Physik. Band 340, Nr. 10, 1911, S. 898–908 (uni-augsburg.de [PDF]).
C. M. Will: The Confrontation between General Relativity and Experiment. In: Living Rev. Relativity. Band 9, 2006, S. 39 (livingreviews.org).
F. W. Dyson, A. S. Eddington, C. Davidson: A determination of the deflection of light by the Sun's gravitational field, from observations made at the total eclipse of 29 May 1919. In: Philos. Trans. Royal Soc. London. 220A, 1920, S. 291–333.
Rosenthal-Schneider, Ilse: Reality and Scientific Truth. Detroit: Wayne State University Press, 1980. S. 74. See also Alice Calapric: The New Quotable Einstein. Princeton: Princeton University Press, 2005, S. 227.
Daniel Kennefick, „Not Only Because of Theory: Dyson, Eddington and the Competing Myths of the 1919 Eclipse Expedition,“ Proceedings of the 7th Conference on the History of General Relativity, Tenerife, 2005; arxiv:0709.0685
Philip Ball: Arthur Eddington was innocent! In: news@nature. 2007, doi:10.1038/news070903-20.
Daniel Kennefick, „Testing relativity from the 1919 eclipse - a question of bias,“ Physics Today, March 2009, S. 37–42.
Albert Einstein: Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen. In: Jahrbuch der Radioaktivität und Elektronik. Band 4, 1908, S. 411–462 (soso.ch [PDF]).
R. V. Pound, G. A. Rebka Jr.: Gravitational Red-Shift in Nuclear Resonance. In: Physical Review Letters. Band 3, Nr. 9, 1. November 1959, S. 439–441, doi:10.1103/PhysRevLett.3.439, bibcode:1959PhRvL...3..439P.
R. V. Pound, G. A. Rebka Jr.: Apparent weight of photons. In: Physical Review Letters. Band 4, Nr. 7, 1. April 1960, S. 337–341, doi:10.1103/PhysRevLett.4.337, bibcode:1960PhRvL...4..337P.
R. H. Dicke: New Research on Old Gravitation: Are the observed physical constants independent of the position, epoch, and velocity of the laboratory? In: Science. Band 129, Nr. 3349, 6. März 1959, S. 621–624, doi:10.1126/science.129.3349.621, PMID 17735811, bibcode:1959Sci...129..621D.
R. H. Dicke: Mach’s Principle and Equivalence. In: Academic Press (Hrsg.): Evidence for gravitational theories. 1962.
Leonard Isaac Schiff: On Experimental Tests of the General Theory of Relativity. In: American Journal of Physics. Band 28, Nr. 4, 1. April 1960, S. 340–343, doi:10.1119/1.1935800, bibcode:1960AmJPh..28..340S.
C. H. Brans, R. H. Dicke: Mach’s Principle and a Relativistic Theory of Gravitation. In: Physical Review. Band 124, Nr. 3, 1. November 1961, S. 925–935, doi:10.1103/PhysRev.124.925, bibcode:1961PhRv..124..925B.
E. B. Fomalont, S. M. Kopeikin, G. Lanyi, J. Benson: Progress in Measurements of the Gravitational Bending of Radio Waves Using the VLBA. In: Astrophysical Journal. Band 699, Nr. 2, Juli 2009, S. 1395–1402, doi:10.1088/0004-637X/699/2/1395, bibcode:2009ApJ...699.1395F.
S. S. Shapiro, J. L. Davis, D. E. Lebach, J. S. Gregory: Measurement of the solar gravitational deflection of radio waves using geodetic very-long-baseline interferometry data, 1979–1999. In: American Physical Society (Hrsg.): Physical Review Letters. Band 92, Nr. 121101, 26. März 2004, S. 121101, doi:10.1103/PhysRevLett.92.121101, PMID 15089661, bibcode:2004PhRvL..92l1101S.
M. Froeschlé, F. Mignard und F. Arenou, „Determination of the PPN parameter γ with the Hipparcos data“ Hipparcos Venice '97, ESA-SP-402 (1997).
I. I. Shapiro: Fourth test of general relativity. In: Physical Review Letters. Band 13, Nr. 26, 28. Dezember 1964, S. 789–791, doi:10.1103/PhysRevLett.13.789, bibcode:1964PhRvL..13..789S.
I. I. Shapiro, M. E. Ash, R. P. Ingalls, W. B. Smith, D. B. Campbell, R. B. Dyce, R. F. Jurgens und Gordon Pettengill: Fourth Test of General Relativity: New Radar Result. In: Physical Review Letters. Band 26, Nr. 18, 3. Mai 1971, S. 1132–1135, doi:10.1103/PhysRevLett.26.1132, bibcode:1971PhRvL..26.1132S.
B. Bertotti, L. Iess, P. Tortora: A test of general relativity using radio links with the Cassini spacecraft. In: Nature. Band 425, 2003, S. 374, doi:10.1038/nature01997, bibcode:2003Natur.425..374B.
S. M. Kopeikin et al.: Gravimagnetic effect of the barycentric motion of the Sun and determination of the post-Newtonian parameter γ in the Cassini experiment. In: Physics Letters A. Band 367, 2007, S. 76, doi:10.1016/j.physleta.2007.03.036, arxiv:gr-qc/0604060, bibcode:2007PhLA..367..276K.
E. B. Fomalont, S. M. Kopeikin: The Measurement of the Light Deflection from Jupiter: Experimental Results. In: Astrophysical Journal. Band 598, Nr. 1, November 2003, S. 704–711, doi:10.1086/378785, arxiv:astro-ph/0302294, bibcode:2003ApJ...598..704F.
E. B. Fomalont, S. M. Kopeikin, D. Jones, M. Honma, O. Titov: Recent VLBA/VERA/IVS tests of general relativity. In: Proceedings of the International Astronomical Union, IAU Symposium. Band 261, S261, Januar 2010, S. 291–295, doi:10.1017/S1743921309990536, bibcode:2010IAUS..261..291F.
K. Nordtvedt Jr.: Equivalence Principle for Massive Bodies. II. Theory. In: Physical Review. Band 169, Nr. 5, 25. Mai 1968, S. 1017–1025, doi:10.1103/PhysRev.169.1017, bibcode:1968PhRv..169.1017N.
K. Nordtvedt Jr.: Testing Relativity with Laser Ranging to the Moon. In: Physical Review. Band 170, Nr. 5, 25. Juni 1968, S. 1186–1187, doi:10.1103/PhysRev.170.1186, bibcode:1968PhRv..170.1186N.
J. G. Williams; Slava G. Turyshev, Dale H. Boggs: Progress in Lunar Laser Ranging Tests of Relativistic Gravity. In: Physical Review Letters. Band 93, Nr. 5, 29. Dezember 2004, S. 1017–1025, doi:10.1103/PhysRevLett.93.261101, arxiv:gr-qc/0411113, bibcode:2004PhRvL..93z1101W.
R. F. C. Vessot; M. W. Levine, E. M. Mattison, E. L. Blomberg, T. E. Hoffman, G. U. Nystrom, B. F. Farrel, R. Decher, P. B. Eby, C. R. Baugher, J. W. Watts, D. L. Teuber and F. D. Wills: Test of Relativistic Gravitation with a Space-Borne Hydrogen Maser. In: Physical Review Letters. Band 45, Nr. 26, 29. Dezember 1980, S. 2081–2084, doi:10.1103/PhysRevLett.45.2081, bibcode:1980PhRvL..45.2081V.
N. Ashby, 2003
J. Hafele, R. Keating: Around the world atomic clocks: predicted relativistic time gains. In: Science. Band 177, Nr. 4044, 14. Juli 1972, S. 166–168, doi:10.1126/science.177.4044.166, PMID 17779917, bibcode:1972Sci...177..166H.
J. Hafele, R. Keating: Around the world atomic clocks: observed relativistic time gains. In: Science. Band 177, Nr. 4044, 14. Juli 1972, S. 168–170, doi:10.1126/science.177.4044.168, PMID 17779918, bibcode:1972Sci...177..168H.
C. W. Chou, D. B. Hume, T. Rosenband, D. J. Wineland: Optical Clocks and Relativity. In: Science. Band 329, Nr. 5999, 2010, S. 1630–1633, doi:10.1126/science.1192720, bibcode:2010Sci...329.1630C.
Tobias Bothwell, Colin J. Kennedy, Alexander Aeppli, Dhruv Kedar, John M. Robinson: Resolving the gravitational redshift across a millimetre-scale atomic sample. In: Nature. Band 602, Nr. 7897, Februar 2022, ISSN 1476-4687, S. 420–424, doi:10.1038/s41586-021-04349-7 (nature.com [abgerufen am 21. Februar 2022]).
I. Ciufolini, E. C. Pavlis: A confirmation of the general relativistic prediction of the Lense–Thirring effect. In: Nature. Band 431, Nr. 7011, 2004, S. 958–960, doi:10.1038/nature03007, PMID 15496915, bibcode:2004Natur.431..958C.
Lorenzo Iorio: Conservative evaluation of the uncertainty in the LAGEOS-LAGEOS II Lense–Thirring test. In: Central European Journal of Physics. Band 8, Nr. 1, 2009, S. 25, doi:10.2478/s11534-009-0060-6, bibcode:2010CEJPh...8...25I.
Lorenzo Iorio: COMMENTS, REPLIES AND NOTES: A note on the evidence of the gravitomagnetic field of Mars. In: Classical Quantum Gravity. Band 23, Nr. 17, 2006, S. 5451–5454, doi:10.1088/0264-9381/23/17/N01, arxiv:gr-qc/0606092, bibcode:2006CQGra..23.5451I.
K. Krogh: Comment on 'Evidence of the gravitomagnetic field of Mars'. In: Classical Quantum Gravity. Band 24, Nr. 22, 2007, S. 5709–5715, doi:10.1088/0264-9381/24/22/N01, bibcode:2007CQGra..24.5709K.
Lorenzo Iorio: On the Lense–Thirring test with the Mars Global Surveyor in the gravitational field of Mars. In: Central European Journal of Physics. 2009, doi:10.2478/s11534-009-0117-6, arxiv:gr-qc/0701146, bibcode:2010CEJPh...8..509I.
Everitt et al.: Gravity Probe B: Final Results of a Space Experiment to Test General Relativity. In: Physical Review Letters. Band 106, Nr. 22, 2011, S. 221101, doi:10.1103/PhysRevLett.106.221101, arxiv:1105.3456.
Lorenzo Iorio: Advances in the Measurement of the Lense–Thirring Effect with Planetary Motions in the Field of the Sun. In: Scholarly Research Exchange. Band 2008, 2008, 105235, S. 1, doi:10.3814/2008/105235, bibcode:2008ScReE2008.5235I.
David Merritt, T. Alexander, S. Mikkola, C. Will: Testing Properties of the Galactic Center Black Hole Using Stellar Orbits. In: The Physical Review D. Band 81, Nr. 6, 2010, S. 062002, doi:10.1103/PhysRevD.81.062002, bibcode:2010PhRvD..81f2002M.
Clifford Will: Testing the General Relativistic „No-Hair“ Theorems Using the Galactic Center Black Hole Sagittarius A*. In: Astrophysical Journal Letters. Band 674, Nr. 1, 2008, S. L25–L28, doi:10.1086/528847, bibcode:2008ApJ...674L..25W.
M. Kramer et al.: Tests of general relativity from timing the double pulsar. In: Science. Band 314, Nr. 5796, 2006, S. 97–102, doi:10.1126/science.1132305, PMID 16973838, arxiv:astro-ph/0609417, bibcode:2006Sci...314...97K.
B. P. Abbott et al.: Observation of Gravitational Waves from a Binary Black Hole Merger (PDF), LIGO Scientific Collaboration and Virgo Collaboration, Physical Review Letters, 11. Februar 2016
P. J. E. Peebles: Testing general relativity on the scales of cosmology. In: World Scientific Publishing Co. Pte. Ltd. Dezember 2004, doi:10.1142/9789812701688_0010, arxiv:astro-ph/0410284, bibcode:2005grg..conf..106P.
G. Lemaître: Expansion of the universe, A homogeneous universe of constant mass and increasing radius accounting for the radial velocity of extra-galactic nebulæ. In: Monthly Notices of the Royal Astronomical Society. Band 91, 1931, S. 483–490, bibcode:1931MNRAS..91..483L. (Übersetzung von Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques, 1927).
Kragh, 2003, S. 152
Kragh, 2003, S. 153.
Pauli, 1958, S. 219–220
Edward Arthur Milne: Relativity, gravitation and world-structure. Hrsg.: Clarendon Press. Oxford 1935.
Chandrasekhar, 1980, S. 37

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Ein1914-1] Albert Einstein: Die formale Grundlage der allgemeinen Relativitätstheorie. In: Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin. Band 46, 1914, S. 1030–1085 (archive.org).

[Ein1915-2] Albert Einstein: Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie. In: Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin. Band 47, 1915, S. 831–839 (archive.org).

[Ein1916-3] Albert Einstein: Die Grundlage der allgemeinen Relativitätstheorie. In: Annalen der Physik. Band 49, 1916, S. 769–782 (uni-augsburg.de [PDF]).

[Verrier-4] U. Le Verrier (1859), (in French), „Lettre de M. Le Verrier à M. Faye sur la théorie de Mercure et sur le mouvement du périhélie de cette planète“, Comptes rendus hebdomadaires des séances de l'Académie des sciences (Paris), vol. 49 (1859), S. 379–383.

[Chow-5] Tai L. Chow,: Gravity, black holes, and the very early universe: an introduction to general relativity and cosmology. Hrsg.: Springer. 2008, ISBN 0-387-73629-8, S. 70.

[Matzner-6] Richard Alfred Matzner: Dictionary of geophysics, astrophysics, and astronomy. Hrsg.: CRC Press. 2001, ISBN 0-8493-2891-8, S. 356.

[weisberg-7] Weisberg et al.: The Relativistic Binary Pulsar B1913+16: Thirty Years of Observations and Analysis. In: Astronomical Society of the Pacific (Hrsg.): ASP Conference Series. 328 Binary Radio Pulsars.. San Francisco Juli 2005, S. 25, arxiv:astro-ph/0407149, bibcode:2005ASPC..328...25W (aspbooks.org).

[soldner-8] Johann Georg von Soldner: Ueber die Ablenkung eines Lichtstrals von seiner geradlinigen Bewegung, durch die Attraktion eines Weltkörpers, an welchem er nahe vorbei geht. In: Astronomisches Jahrbuch für das Jahr 1804. 1804, S. 161–172.

[Einst11-9] Albert Einstein: Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes. In: Annalen der Physik. Band 340, Nr. 10, 1911, S. 898–908 (uni-augsburg.de [PDF]).

[will06-10] C. M. Will: The Confrontation between General Relativity and Experiment. In: Living Rev. Relativity. Band 9, 2006, S. 39 (livingreviews.org).

[Dyson-11] F. W. Dyson, A. S. Eddington, C. Davidson: A determination of the deflection of light by the Sun's gravitational field, from observations made at the total eclipse of 29 May 1919. In: Philos. Trans. Royal Soc. London. 220A, 1920, S. 291–333.

[Rosenthal-12] Rosenthal-Schneider, Ilse: Reality and Scientific Truth. Detroit: Wayne State University Press, 1980. S. 74. See also Alice Calapric: The New Quotable Einstein. Princeton: Princeton University Press, 2005, S. 227.

[Kennefick-13] Daniel Kennefick, „Not Only Because of Theory: Dyson, Eddington and the Competing Myths of the 1919 Eclipse Expedition,“ Proceedings of the 7th Conference on the History of General Relativity, Tenerife, 2005; arxiv:0709.0685

[ball-14] Philip Ball: Arthur Eddington was innocent! In: news@nature. 2007, doi:10.1038/news070903-20.

[PhysToday-15] Daniel Kennefick, „Testing relativity from the 1919 eclipse - a question of bias,“ Physics Today, March 2009, S. 37–42.

[Einst08-16] Albert Einstein: Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen. In: Jahrbuch der Radioaktivität und Elektronik. Band 4, 1908, S. 411–462 (soso.ch [PDF]).

[pound1-17] R. V. Pound, G. A. Rebka Jr.: Gravitational Red-Shift in Nuclear Resonance. In: Physical Review Letters. Band 3, Nr. 9, 1. November 1959, S. 439–441, doi:10.1103/PhysRevLett.3.439, bibcode:1959PhRvL...3..439P.

[pound2-18] R. V. Pound, G. A. Rebka Jr.: Apparent weight of photons. In: Physical Review Letters. Band 4, Nr. 7, 1. April 1960, S. 337–341, doi:10.1103/PhysRevLett.4.337, bibcode:1960PhRvL...4..337P.

[dicke1-19] R. H. Dicke: New Research on Old Gravitation: Are the observed physical constants independent of the position, epoch, and velocity of the laboratory? In: Science. Band 129, Nr. 3349, 6. März 1959, S. 621–624, doi:10.1126/science.129.3349.621, PMID 17735811, bibcode:1959Sci...129..621D.

[dicke2-20] R. H. Dicke: Mach’s Principle and Equivalence. In: Academic Press (Hrsg.): Evidence for gravitational theories. 1962.

[schiff-21] Leonard Isaac Schiff: On Experimental Tests of the General Theory of Relativity. In: American Journal of Physics. Band 28, Nr. 4, 1. April 1960, S. 340–343, doi:10.1119/1.1935800, bibcode:1960AmJPh..28..340S.

[Brans-22] C. H. Brans, R. H. Dicke: Mach’s Principle and a Relativistic Theory of Gravitation. In: Physical Review. Band 124, Nr. 3, 1. November 1961, S. 925–935, doi:10.1103/PhysRev.124.925, bibcode:1961PhRv..124..925B.

[Fomalont-23] E. B. Fomalont, S. M. Kopeikin, G. Lanyi, J. Benson: Progress in Measurements of the Gravitational Bending of Radio Waves Using the VLBA. In: Astrophysical Journal. Band 699, Nr. 2, Juli 2009, S. 1395–1402, doi:10.1088/0004-637X/699/2/1395, bibcode:2009ApJ...699.1395F.

[ShapiroS-24] S. S. Shapiro, J. L. Davis, D. E. Lebach, J. S. Gregory: Measurement of the solar gravitational deflection of radio waves using geodetic very-long-baseline interferometry data, 1979–1999. In: American Physical Society (Hrsg.): Physical Review Letters. Band 92, Nr. 121101, 26. März 2004, S. 121101, doi:10.1103/PhysRevLett.92.121101, PMID 15089661, bibcode:2004PhRvL..92l1101S.

[Froe-25] M. Froeschlé, F. Mignard und F. Arenou, „Determination of the PPN parameter γ with the Hipparcos data“ Hipparcos Venice '97, ESA-SP-402 (1997).

[Shapiro-26] I. I. Shapiro: Fourth test of general relativity. In: Physical Review Letters. Band 13, Nr. 26, 28. Dezember 1964, S. 789–791, doi:10.1103/PhysRevLett.13.789, bibcode:1964PhRvL..13..789S.

[Shapiro2-27] I. I. Shapiro, M. E. Ash, R. P. Ingalls, W. B. Smith, D. B. Campbell, R. B. Dyce, R. F. Jurgens und Gordon Pettengill: Fourth Test of General Relativity: New Radar Result. In: Physical Review Letters. Band 26, Nr. 18, 3. Mai 1971, S. 1132–1135, doi:10.1103/PhysRevLett.26.1132, bibcode:1971PhRvL..26.1132S.

[Bertotti-28] B. Bertotti, L. Iess, P. Tortora: A test of general relativity using radio links with the Cassini spacecraft. In: Nature. Band 425, 2003, S. 374, doi:10.1038/nature01997, bibcode:2003Natur.425..374B.

[Kopeikin-29] S. M. Kopeikin et al.: Gravimagnetic effect of the barycentric motion of the Sun and determination of the post-Newtonian parameter γ in the Cassini experiment. In: Physics Letters A. Band 367, 2007, S. 76, doi:10.1016/j.physleta.2007.03.036, arxiv:gr-qc/0604060, bibcode:2007PhLA..367..276K.

[Fomalont2-30] E. B. Fomalont, S. M. Kopeikin: The Measurement of the Light Deflection from Jupiter: Experimental Results. In: Astrophysical Journal. Band 598, Nr. 1, November 2003, S. 704–711, doi:10.1086/378785, arxiv:astro-ph/0302294, bibcode:2003ApJ...598..704F.

[Fomalont3-31] E. B. Fomalont, S. M. Kopeikin, D. Jones, M. Honma, O. Titov: Recent VLBA/VERA/IVS tests of general relativity. In: Proceedings of the International Astronomical Union, IAU Symposium. Band 261, S261, Januar 2010, S. 291–295, doi:10.1017/S1743921309990536, bibcode:2010IAUS..261..291F.

[Nordtvedt1-32] K. Nordtvedt Jr.: Equivalence Principle for Massive Bodies. II. Theory. In: Physical Review. Band 169, Nr. 5, 25. Mai 1968, S. 1017–1025, doi:10.1103/PhysRev.169.1017, bibcode:1968PhRv..169.1017N.

[Nordtvedt2-33] K. Nordtvedt Jr.: Testing Relativity with Laser Ranging to the Moon. In: Physical Review. Band 170, Nr. 5, 25. Juni 1968, S. 1186–1187, doi:10.1103/PhysRev.170.1186, bibcode:1968PhRv..170.1186N.

[Williams-34] J. G. Williams; Slava G. Turyshev, Dale H. Boggs: Progress in Lunar Laser Ranging Tests of Relativistic Gravity. In: Physical Review Letters. Band 93, Nr. 5, 29. Dezember 2004, S. 1017–1025, doi:10.1103/PhysRevLett.93.261101, arxiv:gr-qc/0411113, bibcode:2004PhRvL..93z1101W.

[Vessot-35] R. F. C. Vessot; M. W. Levine, E. M. Mattison, E. L. Blomberg, T. E. Hoffman, G. U. Nystrom, B. F. Farrel, R. Decher, P. B. Eby, C. R. Baugher, J. W. Watts, D. L. Teuber and F. D. Wills: Test of Relativistic Gravitation with a Space-Borne Hydrogen Maser. In: Physical Review Letters. Band 45, Nr. 26, 29. Dezember 1980, S. 2081–2084, doi:10.1103/PhysRevLett.45.2081, bibcode:1980PhRvL..45.2081V.

[36] N. Ashby, 2003

[Hafele1-37] J. Hafele, R. Keating: Around the world atomic clocks: predicted relativistic time gains. In: Science. Band 177, Nr. 4044, 14. Juli 1972, S. 166–168, doi:10.1126/science.177.4044.166, PMID 17779917, bibcode:1972Sci...177..166H.

[Hafele2-38] J. Hafele, R. Keating: Around the world atomic clocks: observed relativistic time gains. In: Science. Band 177, Nr. 4044, 14. Juli 1972, S. 168–170, doi:10.1126/science.177.4044.168, PMID 17779918, bibcode:1972Sci...177..168H.

[Chou-39] C. W. Chou, D. B. Hume, T. Rosenband, D. J. Wineland: Optical Clocks and Relativity. In: Science. Band 329, Nr. 5999, 2010, S. 1630–1633, doi:10.1126/science.1192720, bibcode:2010Sci...329.1630C.

[40] Tobias Bothwell, Colin J. Kennedy, Alexander Aeppli, Dhruv Kedar, John M. Robinson: Resolving the gravitational redshift across a millimetre-scale atomic sample. In: Nature. Band 602, Nr. 7897, Februar 2022, ISSN 1476-4687, S. 420–424, doi:10.1038/s41586-021-04349-7 (nature.com [abgerufen am 21. Februar 2022]).

[Ciufolini-41] I. Ciufolini, E. C. Pavlis: A confirmation of the general relativistic prediction of the Lense–Thirring effect. In: Nature. Band 431, Nr. 7011, 2004, S. 958–960, doi:10.1038/nature03007, PMID 15496915, bibcode:2004Natur.431..958C.

[Iorio2-42] Lorenzo Iorio: Conservative evaluation of the uncertainty in the LAGEOS-LAGEOS II Lense–Thirring test. In: Central European Journal of Physics. Band 8, Nr. 1, 2009, S. 25, doi:10.2478/s11534-009-0060-6, bibcode:2010CEJPh...8...25I.

[Iorio3-43] Lorenzo Iorio: COMMENTS, REPLIES AND NOTES: A note on the evidence of the gravitomagnetic field of Mars. In: Classical Quantum Gravity. Band 23, Nr. 17, 2006, S. 5451–5454, doi:10.1088/0264-9381/23/17/N01, arxiv:gr-qc/0606092, bibcode:2006CQGra..23.5451I.

[Krogh-44] K. Krogh: Comment on 'Evidence of the gravitomagnetic field of Mars'. In: Classical Quantum Gravity. Band 24, Nr. 22, 2007, S. 5709–5715, doi:10.1088/0264-9381/24/22/N01, bibcode:2007CQGra..24.5709K.

[Iorio4-45] Lorenzo Iorio: On the Lense–Thirring test with the Mars Global Surveyor in the gravitational field of Mars. In: Central European Journal of Physics. 2009, doi:10.2478/s11534-009-0117-6, arxiv:gr-qc/0701146, bibcode:2010CEJPh...8..509I.

[Everitt-46] Everitt et al.: Gravity Probe B: Final Results of a Space Experiment to Test General Relativity. In: Physical Review Letters. Band 106, Nr. 22, 2011, S. 221101, doi:10.1103/PhysRevLett.106.221101, arxiv:1105.3456.

[Iorio5-47] Lorenzo Iorio: Advances in the Measurement of the Lense–Thirring Effect with Planetary Motions in the Field of the Sun. In: Scholarly Research Exchange. Band 2008, 2008, 105235, S. 1, doi:10.3814/2008/105235, bibcode:2008ScReE2008.5235I.

[Merritt-48] David Merritt, T. Alexander, S. Mikkola, C. Will: Testing Properties of the Galactic Center Black Hole Using Stellar Orbits. In: The Physical Review D. Band 81, Nr. 6, 2010, S. 062002, doi:10.1103/PhysRevD.81.062002, bibcode:2010PhRvD..81f2002M.

[Will08-49] Clifford Will: Testing the General Relativistic „No-Hair“ Theorems Using the Galactic Center Black Hole Sagittarius A*. In: Astrophysical Journal Letters. Band 674, Nr. 1, 2008, S. L25–L28, doi:10.1086/528847, bibcode:2008ApJ...674L..25W.

[Kramer-50] M. Kramer et al.: Tests of general relativity from timing the double pulsar. In: Science. Band 314, Nr. 5796, 2006, S. 97–102, doi:10.1126/science.1132305, PMID 16973838, arxiv:astro-ph/0609417, bibcode:2006Sci...314...97K.

[Abbottetal-51] B. P. Abbott et al.: Observation of Gravitational Waves from a Binary Black Hole Merger (PDF), LIGO Scientific Collaboration and Virgo Collaboration, Physical Review Letters, 11. Februar 2016

[Peebles-52] P. J. E. Peebles: Testing general relativity on the scales of cosmology. In: World Scientific Publishing Co. Pte. Ltd. Dezember 2004, doi:10.1142/9789812701688_0010, arxiv:astro-ph/0410284, bibcode:2005grg..conf..106P.

[Lem-53] G. Lemaître: Expansion of the universe, A homogeneous universe of constant mass and increasing radius accounting for the radial velocity of extra-galactic nebulæ. In: Monthly Notices of the Royal Astronomical Society. Band 91, 1931, S. 483–490, bibcode:1931MNRAS..91..483L. (Übersetzung von Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques, 1927).

[54] Kragh, 2003, S. 152

[55] Kragh, 2003, S. 153.

[56] Pauli, 1958, S. 219–220

[Milne-57] Edward Arthur Milne: Relativity, gravitation and world-structure. Hrsg.: Clarendon Press. Oxford 1935.

[58] Chandrasekhar, 1980, S. 37