Abstand
Der Abstand, auch die Entfernung oder die Distanz zweier Punkte ist die Länge der kürzesten Verbindung dieser Punkte.

Im euklidischen Raum ist dies die Länge der geradlinigen Strecke zwischen den beiden Punkten. Der Abstand zweier geometrischer Objekte ist die Länge der kürzesten Verbindungslinie der beiden Gegenstände, also der Abstand der beiden einander nächstliegenden Punkte. Werden nicht die einander nächstliegenden Punkte zweier Objekte betrachtet, so wird dies explizit angegeben oder ergibt sich aus dem Zusammenhang, wie beispielsweise der Abstand der geometrischen Mittelpunkte oder der Schwerpunkte.
Die Metrik ist der Teil der Mathematik, der sich mit der Abstandsmessung beschäftigt.
Der Abstand, die Entfernung, die Distanz zwischen zwei Werten einer Größe oder zwischen zwei Zeitpunkten wird bestimmt, indem man den Absolutbetrag ihrer Differenz bildet, das heißt, indem sie voneinander abgezogen werden und vom Ergebnis der Absolutbetrag gebildet wird. Der gemessene Abstand ist unabhängig vom gewählten Referenzpunkt des Koordinatensystems, nicht aber von dessen Skalierung (siehe auch Maßstabsfaktor).
In der beobachtenden Astronomie wird der scheinbare Abstand am Himmel zwischen zwei Himmelsobjekten als Winkelabstand angegeben.
Der Abstand zweier Mengen im euklidischen Raum (oder allgemeiner in einem metrischen Raum) kann über die Hausdorff-Metrik definiert werden.
Euklidischer Abstand
Im kartesischen Koordinatensystem berechnet man den Abstand (euklidischer Abstand) zweier Punkte mit Hilfe des Satzes von Pythagoras:
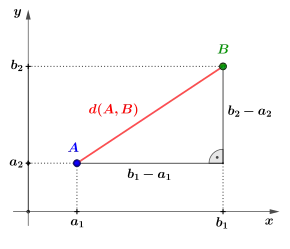
Für die Ebene ():
Für den dreidimensionalen Raum ():
Der Abstand eines Punkts von einer Geraden oder einer ebenen Fläche ist der Abstand vom Fußpunkt des darauf gefällten Lots, der von einer gekrümmten Linie ist stets ein Abstand von einer ihrer Tangenten.
Berechnungsmöglichkeiten für die Abstände von Punkten zu Geraden oder Ebenen sind in der Formelsammlung analytische Geometrie aufgeführt.
Abstand zwischen Punkt und Gerade
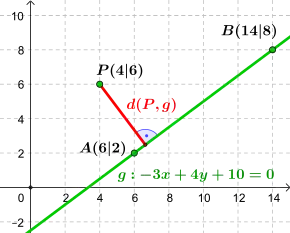
Der Abstand zwischen dem Punkt und der Geraden mit der Koordinatenform beträgt:
Der Punkt auf der Geraden , der am nächsten liegt, hat die Koordinaten
Wenn die Gerade durch die Punkte und verläuft, ist
Diese Werte können in die Formeln eingesetzt werden.[3]
Beispiel
Eingesetzte Werte für Gerade : und für Punkt
- [LE]
Abstand im dreidimensionalen Raum
Für die Konstruktion des Abstandes bedarf es als zusätzliches Hilfsmittel einer Dynamischen-Geometrie-Software (DGS).
Abstand zwischen Punkt und Gerade
Der Abstand zwischen dem Punkt und der Geraden , die durch die Punkte und verläuft, beträgt mit den Vektoren :
Beispiel
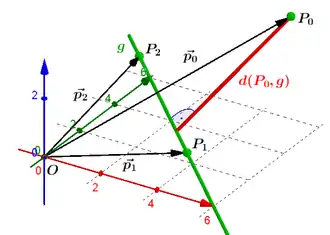
Konstruktion des Abstandes .
Gegeben sind die Koordinaten der Punkte und , durch die die Gerade verläuft, und der Punkt .
Nach dem Einzeichnen der Geraden durch , und dem Punkt werden die Verbindungsvektoren und eingezeichnet. Eine abschließend errichtete Senkrechte auf die Gerade durch Punkt liefert den Abstand [LE].
Nachrechnung
Diese Werte in die Formel eingesetzt, ergeben
- [LE].
Abstand zwischen zwei windschiefen Geraden
Zwei windschiefe Geraden (), wobei die eine durch die Punkte und und die andere durch die Punkte und verläuft, haben mit den Vektoren folgenden Abstand:
Beispiel
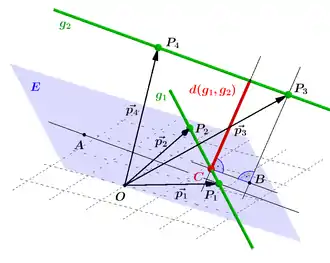
Konstruktion des Abstandes mithilfe einer Hilfsebene.
Gegeben seien die Koordinaten der vier Punkte und
Nach dem Einzeichnen der Geraden durch , und durch , werden zunächst die Verbindungsvektoren und eingezeichnet. Für das Bestimmen der Hilfsebene wird eine Parallele zu durch gezogen und anschließend der Punkt beliebig auf der Parallele markiert. Mithilfe der somit gegebenen drei Punktes und wird die Ebene generiert. Es folgt das Fällen des Lots vom Punkt auf die Ebene mit Fußpunkt und eine Parallele zu die in (rot) schneidet. Abschließend liefert die Parallele zu ab dem Punkt bis zur Geraden den Abstand: [LE].
Nachrechnung
Diese Werte eingesetzt in die Formel ergeben
- [LE].
Abstand zwischen Punkt und Ebene
Der Abstand zwischen dem Punkt und der Ebene mit der Koordinatenform [A 1] beträgt:
Für die einzusetzenden Werte gilt:
Wenn drei Punkte , , gegeben sind, die eine Ebene bestimmen (siehe Dreipunkteform) dann lässt sich der Abstand mithilfe der Vektoren mit folgender Formel berechnen:
Dabei steht für das Kreuzprodukt, für das Skalarprodukt und für den Betrag des Vektors.
Beispiel
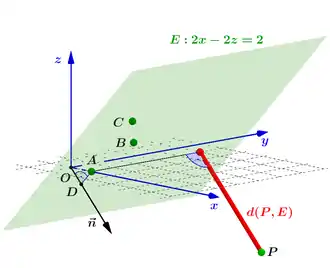
Konstruktion des Abstandes [7]
Gegeben seien die Koordinaten der drei Punkte der Ebene mit sowie des außerhalb liegenden Punktes
Nach dem Eintragen der Punkte und sowie des außerhalb liegenden Punktes kann die Ebene generiert werden. Anschließend fällt man das Lot vom Punkt des Koordinatenursprungs auf die Ebene mit dem Fußpunkt Durch die Punkte und verläuft auch der, aus der Parameterdarstellung von ermittelbare, Normalenvektor mit Abschließend liefert die Parallele zu ab dem Punkt bis zur Ebene den Abstand: [LE].
Nachrechnung
Ermittlung der einzusetzenden Werte für Formel
Diese Werte eingesetzt in ergeben schließlich
- [LE].
Das Ergebnis gleicht dem des Beispiels.
Andere Definitionen
Die Definition des euklidischen Abstands kann mithilfe von Metriken verallgemeinert werden. Der euklidische Abstand ist der euklidischen Norm (2-Norm) eines Vektorraums, z. B. des dreidimensionalen euklidischen Raums, zugeordnet, siehe Metrischer Raum - Beispiele.
Manhattan-Metrik
Die sogenannte Manhattan-Metrik ist eine Metrik, in der den Abstand zwischen zwei Punkten und als die Summe der absoluten Differenzen ihrer Einzelkoordinaten definiert wird:[8]
Die Manhattan-Metrik ist die von der Summennorm (1-Norm) eines Vektorraums erzeugte Metrik.
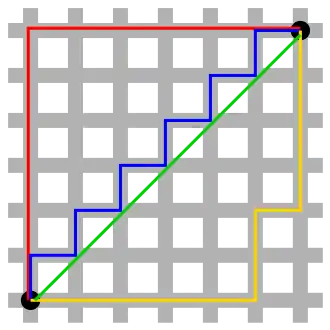
Weil die Wege zwischen zwei Punkten immer rechtwinklig entlang den horizontalen und vertikalen Linien (Straßen) verlaufen, aber nicht durch die quadratischen "Gebäudeblöcke", ist der Abstand zwischen zwei Punkten nicht kleiner und im Allgemeinen größer als der euklidischen Abstand. Der Abstand zwischen zwei Punkten mit ganzzahligen Koordinaten (Kreuzungen) ist immer eine ganze Zahl.
So ist beispielsweise in der nebenstehenden Grafik die Manhattan-Metrik in einem zweidimensionalen Raum, sodass sich
ergibt, wobei und die schwarz markierten Punkte sind.
Abstandsmessung auf gekrümmten Flächen
Auf der Kugeloberfläche wird der Abstand entlang von Großkreisen bestimmt und im Gradmaß oder Bogenmaß angegeben. Zur Berechnung des Abstandes siehe Orthodrome.
Auf dem Erdellipsoid oder anderen konvexen Flächen benutzt man die geodätische Linie oder den Normalschnitt.
In der Geodäsie und den Geowissenschaften spricht man eher von Distanz oder Entfernung, die metrisch angegeben wird.
Dichtestes Punktpaar

Das Problem des dichtesten Punktpaares (englisch closest pair of points problem) ist die Suche nach den zwei am dichtesten beieinander liegenden Punkten in einer Ebene. Gegeben ist eine beliebige Menge von Punkten in der Ebene und gesucht sind zwei dieser Punkte, sodass der euklidische Abstand minimal ist. Ein ähnliches Problem ist die Suche nach den zwei am weitesten voneinander entfernten Punkten in der Ebene, also den zwei Punkten mit dem maximalen euklidischen Abstand.
Der Brute-force-Algorithmus berechnet die Abstände zwischen allen möglichen Punktpaaren und wählt das Punktpaar mit dem kleinsten Abstand aus. Die Laufzeit des Algorithmus ist quadratisch und liegt in . Ein Divide-and-conquer-Algorithmus hat eine Laufzeit, die in liegt.
Siehe auch
Weblinks
Anmerkungen
- Um eine Doppelbezeichnung der Konstante zu vermeiden wurde mit passendem Vorzeichen gewählt.
- Im Gegensatz zur Formel aus dem englischen Sprachraum wurde für den Abstand die Bezeichnung anstatt gewählt.
Einzelnachweise
- Petra Stein, Sven Vollnhals: 3.5.1 Spezialfälle der Minkowski-Metrik: Das euklidische Distanzmaß. 3.5 Distanz- und Ähnlichkeitsmaße für metrische Variablen. In: Grundlagen clusteranalytischer Verfahren. Universität Duisburg-Essen, 1. April 2011, S. 15, abgerufen am 19. Oktober 2018.
- Klaus Hefft: 9.1.3 Euklidischer Raum. 9.1 Dreidimensionaler euklidischer Raum. In: MATHEMATISCHER VORKURS zum Studium der Physik. Universität Heidelberg, 8. Juli 2018, abgerufen am 19. Oktober 2018.
- Wolfram MathWorld: Point-Line Distance--2-Dimensional
- Wolfram MathWorld: Point-Line Distance--3-Dimensional
- Wolfram MathWorld: Line-Line Distance
- Wolfram MathWorld: Point-Plane Distance
- R. Verfürth: I.5.7. Parameterfreie Darstellungen einer Ebene.; Beispiel I.5.6. Mathematik für Maschinenbauer, Bauingenieure und Umwelttechniker I. Ruhr-Universität Bochum, Dezember 2006, S. 37―39, abgerufen am 22. Mai 2021.
- Wolfram MathWorld: Taxicab Metric