Weltlinie
Weltlinie ist ein Begriff der Relativitätstheorie und bezeichnet die Trajektorie eines Objekts in der Raumzeit.[1]
Relativitätstheorie
Die Weltlinien von frei fallenden Objekten, also Objekten, die nur der Gravitation unterliegen, sind gemäß der Allgemeinen Relativitätstheorie Geodäten in der gekrümmten Raumzeit. Dies gilt auch für Objekte, deren räumliche Bahnen geschlossen sind. So ist in einem relativ zur Sonne ruhenden Bezugssystem die Weltlinie der Erde eine Schraubenlinie, deren Achse die Zeitachse ist.
Im Zusammenhang mit der Speziellen Relativitätstheorie wurde der Begriff der Weltlinie 1908 von Hermann Minkowski eingeführt[2] (siehe auch Minkowski-Diagramm). Weltlinien sind für masselose Teilchen lichtartig und für massebehaftete Objekte zeitartig.
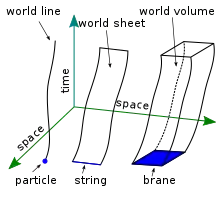
Das Konzept lässt sich auf höherdimensionale Objekte verallgemeinern. So ergibt die Bewegung eines eindimensionalen Strings durch die Raumzeit eine Weltfläche, einem zweidimensionalen Objekt kann man ein Weltvolumen zuordnen usw.
Kosmologie
Auch in Raum-Zeit-Diagrammen der Kosmologie werden Weltlinien gemäß der Allgemeinen Relativitätstheorie verwendet. Basis für die Entwicklung des isotrop und homogen angenommenen Universums ist dabei die Friedmann-Gleichung, zeitlicher Verlauf und Abstände sind durch die Friedmann-Lemaître-Robertson-Walker-Metrik (FLRW-Metrik) induziert. Betrachtet werden zum Beispiel Weltlinien von Galaxien, die unter einer bestimmten Rotverschiebung z heute sichtbar sind, oder Weltlinien von Photonen zwischen der Weltlinie einer Quelle (z. B. einer Galaxie) und der eines Beobachters.
Häufig sieht man Abbildungen mit zwei Koordinatenachsen. Als senkrechte Achse wird das Weltalter seit dem Urknall aufgeführt, wobei die Zeit im Sinne der Allgemeinen Relativitätstheorie als Eigenzeit von mit dem Hubble-Flow treibenden Beobachtern (mit synchronisierten Uhren) verstanden wird.
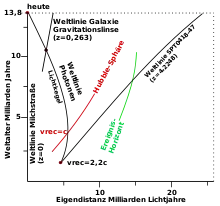
Anders als für die Zeitachse gibt es für die waagerechte Raumachse kein natürliches Maß für die Raumkoordinaten. Entfernungen zwischen Objekten zu konstanter gemeinsamer Zeit existieren, sind jedoch nicht messbar. Vielmehr müssen diese Distanzen über die kosmologische Theorie erschlossen werden. Mitbewegte Koordinaten treiben mit dem Hubble-Flow. Die mitbewegte Distanz (englisch: comoving distance) zwischen Objekten, die ebenfalls im Hubble-Flow treiben, ändert sich trotz der Expansion des Universums nicht. Im Gegensatz dazu machen physikalische Koordinaten die mit der Expansion des Universums anwachsenden Entfernungen zwischen Objekten sichtbar. Aufgrund von Isotropie und Homogenität des Universums kann der Ursprung des Koordinatensystems im Prinzip an einem beliebigen Ort des beobachtbaren Universums angesetzt werden.
Werden astronomische Objekte wie Galaxien abgebildet, so wird üblicherweise auf das (räumlich flache) Standardmodell der Kosmologie (Lambda-CDM-Modell) zurückgegriffen, wobei andere Weltlinien häufig als Abstände zur Weltlinie des Beobachters aufgetragen werden. Im Falle der Verwendung physikalischer Koordinaten übernimmt der mit dem Skalenfaktor multiplizierte mitbewegte Radius r der Friedmann-Gleichung als Eigendistanz (englisch: proper distance) die Abstandsmessung auf der waagerechten Koordinatenachse. Mehrheitlich werden ohne Berücksichtigung von Pekuliarbewegungen nur Entfernungsänderungen aufgrund der Expansion des Universums erfasst.
Die Zeichnung zeigt auf der Basis physikalischer Koordinaten die mit der Galaxie SPT0418-47 verbundenen Weltlinien.[3] Die waagerechte Koordinatenachse ist ohne Raumwinkel in Richtung des radialen Pfads vom Beobachter zu SPT0418-47 gewählt. Erst die Vergrößerung durch eine Gravitationslinse macht diese Galaxie für eine genauere Untersuchung zugänglich.
Einzelnachweise
- Paul A. Tipler, Ralph A. Llewellyn: Moderne Physik. Verlag Oldenbourg, 2002, ISBN 978-3-486-25564-5.
- A. Friedmann, G. Singer: Die Welt als Raum und Zeit. Verlag Harri Deutsch, 3. Auflage, 2006, S. 124, [https://de.wikipedia.org/w/index.php?title=Wikipedia:Defekte_Weblinks&dwl=http://books.google.de/books?id=VIpqvbNACM8C&lpg=PA124&hl=de&pg=PA124#v=onepage&q&f=false Seite nicht mehr abrufbar], Suche in Webarchiven: [http://timetravel.mementoweb.org/list/2010/http://books.google.de/books?id=VIpqvbNACM8C&lpg=PA124&hl=de&pg=PA124#v=onepage&q&f=false Google Books.]
- Siehe Summary und Tabelle der Weltlinien-Zeichnung. Abgerufen am 5. September 2020.