Koordinatensystem

Ein Koordinatensystem dient dazu, Punkte mit Hilfe von Zahlen, den Koordinaten, in eindeutiger Weise zu beschreiben. Die einfachsten Beispiele sind ein Zahlenstrahl und kartesische Koordinaten in der Ebene. Im ersten Fall wird einem Punkt einer Gerade eine reelle Zahl zugeordnet. Im zweiten Fall wird ein Punkt in der Ebene durch zwei reelle Zahlen beschrieben.

Zahlenstrahl (oben), ebene kartesische Koordinaten (unten)

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Die Felder des Schachbretts werden mit einem Zahlen-Buchstaben-Paar bezeichnet.

Bei räumlichen Gebilden sind drei Koordinaten erforderlich, bei raum-zeitlichen Gebilden vier.

Der Begriff Koordinate – in der Bedeutung „Lageangabe“ – wurde im 18. Jahrhundert aus dem Wort Ordinate (Senkrechte) gebildet.[1]

Koordinaten werden in verschiedenen Bereichen der Mathematik und Physik unterschiedlich bezeichnet. So heißen die Koordinaten eines Elements (Vektors) eines endlichdimensionalen Vektorraums seine Komponenten, die Koordinaten in einem Produkt von Mengen sind die Projektionen auf einen der Faktoren. Oft gibt es zahlreiche Möglichkeiten, ein Koordinatensystem einzuführen. Beim Beispiel des Zahlenstrahls hat man beliebig viele Möglichkeiten einen Punkt auszuwählen, dem die Koordinate 0 zugeordnet werden soll. In der Ebene ist die Situation sogar noch komplizierter. Selbst nach Wahl eines Punktes, der die Koordinate $(0,0)$ erhält, lässt sich jedes (verschiedene) Paar von Zahlenstrahlen durch diesen Punkt als Koordinatenachsen wählen.

Je nach Beschaffenheit der Menge, auf der man ein Koordinatensystem wählen möchte benötigt man auch mehr als ein oder zwei Koordinaten. Die geordnete Menge der Koordinaten wird meist als ein n-Tupel bezeichnet. Der Punkt des Zahlenstrahls mit der Koordinate 0 und der Punkt der Ebene mit den Koordinaten $(0,0)$ beziehungsweise der ausgezeichnete Punkt einer Menge, dessen Koordinaten alle 0 sind, wird als Koordinatenursprung (kurz: Ursprung) bezeichnet.

Neben den weit verbreiteten kartesischen (rechtwinkligen) Koordinaten gibt es auch andere Arten, Koordinatensysteme zu definieren. Möchte man beispielsweise auf der Kreisfläche Koordinaten einführen, so würden sich Polarkoordinaten anbieten. Der Kreismittelpunkt wäre dann der Ursprung und jeder Punkt der Kreisfläche würde durch Angabe der Entfernung vom Mittelpunkt und eines Winkels eindeutig beschrieben. In diesem Fall lässt sich im Vergleich zu den kartesischen Koordinaten nur eine der beiden Koordinaten als Länge interpretieren. Ein anderes Beispiel ist das eines Schachbrettes. Hier wird eine Kombination aus Buchstaben und natürlichen Zahlen genutzt, um die Felder des Brettes zu benennen.

In vielen Situationen ist es unmöglich, hinreichend sinnvolle und bequeme globale Koordinaten auf der gesamten Menge einzuführen. Zum Beispiel können die Punkte einer Kugeloberfläche, anders als die einer Ebene, nicht in eine kontinuierliche Eins-zu-Eins-Korrespondenz mit Zahlenpaaren gebracht werden. Daher wurde das Konzept der lokalen Koordinaten eingeführt. Dies ist zum Beispiel die Situation in der Theorie der Mannigfaltigkeiten.

Gebräuchliche Koordinatensysteme

Zahlengerade

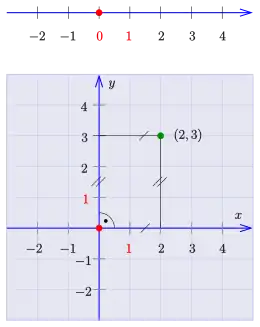
Das einfachste Beispiel eines Koordinatensystems ist die Identifikation von Punkten auf einer Gerade mit der reellen Zahlengerade. In diesem System wird ein beliebiger Punkt O (der Ursprung) auf einer gegebenen Geraden gewählt. Die Koordinate eines Punktes P ist definiert als der vorzeichenbehaftete Abstand von O zu P, wobei der vorzeichenbehaftete Abstand als positiv oder negativ angenommen wird, je nachdem, auf welcher Seite der Linie P liegt. Jeder Punkt erhält eine eindeutige Koordinate und jede reelle Zahl ist die Koordinate eines eindeutigen Punktes.[2]

Die Zahlenlinie

Kartesisches Koordinatensystem

Das kartesische Koordinatensystem im dreidimensionalen Raum

Links- und rechtshändiges (rechts) dreidimensionales Koordinatensystem

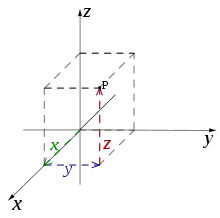
Eines der bekanntesten Beispiele für ein Koordinatensystem ist das kartesische Koordinatensystem. In der Ebene werden zwei Senkrechte gewählt und die Koordinaten eines Punktes als die vorzeichenbehafteten Abstände zu den Geraden aufgefasst. In drei Dimensionen wählt man drei zueinander orthogonale Ebenen und die drei Koordinaten eines Punktes sind die vorzeichenbehafteten Abstände zu jeder der Ebenen. Dies kann verallgemeinert werden, um n-Koordinaten für jeden Punkt im n-dimensionalen euklidischen Raum zu erzeugen.

Es ist nach dem latinisierten Namen Cartesius des französischen Mathematikers René Descartes benannt, der das Konzept der „kartesischen Koordinaten“ bekannt gemacht hat.[3] Je nach Anordnung der Koordinatenachsen kann das dreidimensionale Koordinatensystem ein Rechts- oder ein Linkssystem sein.

Affines Koordinatensystem

affine Koordinaten

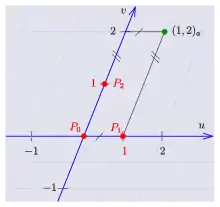
Wählt man in der euklidischen Ebene drei nicht auf einer Gerade liegende Punkte $P_{0},P_{1},P_{2}$ aus, so sind die beiden Vektoren ${\overrightarrow {P_{0}P_{1}}},{\overrightarrow {P_{0}P_{2}}}$ linear unabhängig. Mit dem Punkt $P_{0}$ als Ursprung lässt sich der Ortsvektor ${\overrightarrow {P_{0}P}}$ eines beliebigen Punktes $P$ so schreiben:

{\overrightarrow {P_{0}P}}=u{\overrightarrow {P_{0}P_{1}}}+v{\overrightarrow {P_{0}P_{2}}}

und dem Punkt $P$ das Zahlenpaar $(u,v)_{a}$ als affine Koordinaten[4] bezüglich den Basispunkten $P_{0},P_{1},P_{2}$ zuordnen.

Bilden die Vektoren ${\overrightarrow {P_{0}P_{1}}},{\overrightarrow {P_{0}P_{2}}}$ eine Orthonormalbasis, so ergeben sich die zuvor genannten kartesischen Koordinaten. In diesem Fall sind für einen Punkt $(u_{0},v_{0})_{a}$ die Punktmengen $u=u_{0}$ und $v=v_{0}$ Geraden, die sich orthogonal schneiden. Sind die Basisvektoren nicht orthogonal (siehe Bild), spricht man von schiefwinkligen Koordinaten.

Entsprechend sind affine Koordinaten für höhere Dimensionen erklärt. Koordinaten auf diese Weise zu definieren ist für jeden n-dimensionalen affinen Raum über einem Körper möglich, ist also nicht auf einen euklidischen Raum beschränkt.

Polarkoordinaten

Polarkoordinaten

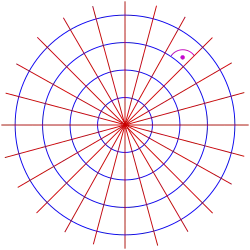
Ein weiteres häufig genutztes Koordinatensystem ist das der Polarkoordinarten. Dieses kann nur in der Ebene eingeführt werden. Für den dreidimensionalen Raum gibt es mit den Kugel- und den Zylinderkoordinaten zwei unterschiedliche Verallgemeinerungen. Im Gegensatz zu den zuvor genannten Systemen sind dieses Koordinatensystem und seine zwei Verallgemeinerungen keine Spezialfälle affiner Koordinatensysteme.

Für die Definition dieses Koordinatensystems wird ein Punkt als Pol und ein Strahl von diesem Punkt wird als Polachse gewählt. Für einen gegebenen Winkel $\phi$ gibt es eine einzige Linie durch den Pol, deren Winkel mit der Polachse $\phi$ ist (gemessen gegen den Uhrzeigersinn von der Achse zur Linie). Dann gibt es einen einzigen Punkt auf dieser Linie, dessen Abstand vom Ursprung den Wert $r$ ist. Für ein gegebenes Koordinatenpaar $(r,\phi )$ gibt es einen einzigen Punkt, aber jeder Punkt wird durch viele Koordinatenpaare dargestellt. Zum Beispiel sind $(r,\phi )$ und $(r,\phi +2\pi )$ Polarkoordinaten für denselben Punkt. Der Pol wird durch $(0,\phi )$ für einen beliebigen Wert von $\phi$ dargestellt.

Kugel- und Zylinderkoordinaten

Zylinderkoordinaten

Kugelkoordinaten

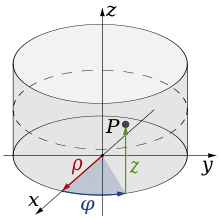
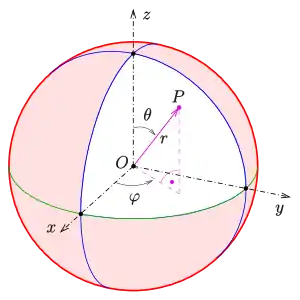
Es gibt zwei übliche Methoden zur Erweiterung der Polarkoordinaten für den dreidimensionalen Raum.

Bei zylindrischen Koordinatensystem wird eine z-Koordinate mit der gleichen Bedeutung wie bei kartesischen Koordinaten zu den Polarkoordinaten $(r,\phi )$ hinzugefügt, was ein Tripel $(r,\phi ,z)$ ergibt.

Bei Kugelkoordinaten oder räumlichen Polarkoordinaten wird ein Punkt im dreidimensionalen Raum durch seinen Abstand vom Ursprung und durch zwei Winkel angegeben. Ein bekanntes Beispiel eines Kugelkoordinatensystems ist das System der Geographischen Koordinaten mit deren Hilfe die Erde in Längen- und Breitengrade unterteilt wird. Die dritte Koordinaten also der Abstand vom Erdmittelpunkt ist bei diesem System nicht relevant.

Elliptische Koordinaten

Elliptische Koordinaten verwenden sich senkrecht schneidende Systeme von konfokalen Ellipsen und Hyperbeln. Diese Koordinaten sind für die Brennpunkte und die Punkte dazwischen nicht definiert.

Den (ebenen) elliptischen Koordinaten entsprechen die Ellipsoid-Koordinaten. Das hier verwendete orthogonale Flächensystem besteht aus konfokalen Ellipsoiden, einschaligen und zweischaligen Hyperboloiden.

Weiterhin gibt es noch die ellipsoidische Koordinaten, die zur Beschreibung von Punkten eines Rotations-Ellipsoids (Erde) verwendet werden.

Parameterdarstellung

Parameterdarstellungen von Flächen kann man als Koordinatensysteme dieser Flächen ansehen. Z. B. die Parameterdarstellung einer Ebene, die übliche Parameterdarstellung einer Kugeloberfläche mit geographischer Länge und Breite oder die Paramerdarstellung eines Ellipsoids.

Lokales Koordinatensystem

Kugelkoordinaten mit zugehöriger lokaler Basis

\mathbf {e} _{r},\mathbf {e} _{\theta },\mathbf {e} _{\varphi }

Ein lokales Koordinatensystem oder auch (Koordinaten-)Karte[5] ist ein Koordinatensystem für eine Teilmenge eines geometrischen Objekts. Das Konzept der Koordinatenkarten ist zentral für die Theorie der Mannigfaltigkeiten. Eine Mannigfaltigkeit ist ein geometrisches Objekt, so dass für jeden Punkt ein lokales Koordinatensystem existiert, das mit den benachbarten Koordinatensystemen verträglich ist. Genauer gesagt ist eine Koordinatenkarte ein Homöomorphismus von einer offenen Teilmenge eines Raumes zu einer offenen Teilmenge von $\mathbb {R} ^{n}$ . Oft ist es nicht möglich, ein einziges konsistentes Koordinatensystem für einen ganzen Raum bereitzustellen. In diesem Fall wird eine Sammlung von Koordinatenkarten zu einem Atlas zusammengesetzt, der den ganzen Raum abdeckt.[6]

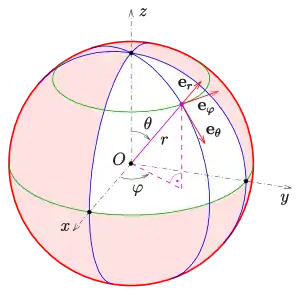
Sind beispielsweise $(u,v)_{c}$ krummlinige orthogonale Koordinaten (Polarkoordinaten, elliptische Koordinaten,...) auf der Ebene und bestimmt man an einem Punkt $P_{0}=(u_{0},v_{0})_{c}$ die Tangentenrichtungen der Kurven $v=v_{0}$ und $u=u_{0}$ und normiert diese, so erhält man lokale Basisvektoren, die man für ein lokales Koordinatensystem verwenden kann. Bei Polarkoordinaten zeigt der eine Vektor in Radiusrichtung und der andere in Richtung der Tangente des Kreises durch $P_{0}$ . Hier kann man sich das lokale System durch Verschiebung und geeigneter Drehung aus dem globalen System entstanden denken.

Im Raum bestimmt man die Tangentenvektoren an die durch einen Punkt $P_{0}=(u_{0},v_{0},w_{0})_{c}$ gehenden Kurven $(u,v_{0},w_{0})_{c}$ , $(u_{0},v,w_{0})_{c}$ und $(u_{0},v_{0},w)_{c}$ und normiert sie.

Koordinatentransformationen

Für das Umrechnen von Koordinaten eines Systems in die Koordinaten eines anderen Systems gibt es die Koordinatentransformationen.

Homogene Koordinaten in der Ebene

Die euklidische Ebene lässt sich auch mit homogenen Koordinaten beschreiben. Dabei werden einem Punkt $P=(x,y)$ drei homogene Koordinaten $(x_{1}:x_{2}:x_{3})$ so zugeordnet, dass auch $P=(cx_{1}:cx_{2}:cx_{3})$ für alle $c\neq 0$ gilt. Eine Standardzuordnung ist $P=(x:y:1)$ . Setzt man $P=(x:y:1-x-y)$ erhält man baryzentrische Koordinaten. Der große Vorteil homogener Koordinaten ist, dass Punkte der Ferngerade einfach zu beschreiben sind: Im Standardfall durch die Gleichung $x_{3}=0$ , im baryzentrischen Fall durch die Gleichung $x_{1}+x_{2}+x_{3}=0$ . Die bei affinen Koordinaten nötigen Grenzwert-Überlegungen werden im Standardfall zum einfachen Setzen von $x_{3}=0$ .

In der Dreiecksgeometrie werden auch trilineare Koordinaten verwendet.

Weitere Koordinatensysteme

Einige nur in Fachgebieten (z. B. Geodäsie, Kartografie, Geographie, Fernerkundung, Astronomie, Amateurfunk) gebräuchliche Koordinatensysteme sind:

Inertialsystem
Geographisches Koordinatensystem
Soldner-Koordinatensystem
Gauß-Krüger-Koordinatensystem
UTM-Koordinatensystem
- UTM-Referenzsystem auch MGRS
Astronomische Koordinatensysteme wie das ekliptikale oder galaktische
Parallele Koordinaten
Bewegte Koordinatensysteme
Rotierende Koordinatensysteme
Fahrzeugkoordinatensystem
Weltkoordinatensystem
QTH-Locator (Amateurfunk)
Marinequadrate und Gradnetze (aus dem Zweiten Weltkrieg)

Weblinks

Wiktionary: Koordinate – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wiktionary: Koordinatensystem – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Einfache und verständliche Erklärung (hpts. durch Abbildungen)
Eric W. Weisstein: Coordinate System. In: MathWorld (englisch).

Einzelnachweise

Etymologie nach Kluge Etymologisches Wörterbuch der deutschen Sprache, 24. Auflage, 2002.
James B. Stewart, Lothar Redlin, Saleem Watson: College Algebra. Hrsg.: Brooks Cole. 5. Auflage. 2008, ISBN 978-0-495-56521-5, S. 13–19.
Kartesische Koordinaten. In: Guido Walz (Hrsg.): Lexikon der Mathematik. 1. Auflage. Spektrum Akademischer Verlag, Mannheim/Heidelberg 2000, ISBN 3-8274-0439-8.
Bronstein, Semendjajew: Taschenbuch der Mathematik, Teubner-Verlag, Leipzig, 1979, ISBN 3 87144 492 8, S. 606
Komplexe Mannigfaltigkeit. In: Guido Walz (Hrsg.): Lexikon der Mathematik. 1. Auflage. Spektrum Akademischer Verlag, Mannheim/Heidelberg 2000, ISBN 3-8274-0439-8.
John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218). Springer-Verlag, New York NY u. a. 2003, ISBN 0-387-95448-1, S. 4ff.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Etymologie nach Kluge Etymologisches Wörterbuch der deutschen Sprache, 24. Auflage, 2002.

[2] James B. Stewart, Lothar Redlin, Saleem Watson: College Algebra. Hrsg.: Brooks Cole. 5. Auflage. 2008, ISBN 978-0-495-56521-5, S. 13–19.

[3] Kartesische Koordinaten. In: Guido Walz (Hrsg.): Lexikon der Mathematik. 1. Auflage. Spektrum Akademischer Verlag, Mannheim/Heidelberg 2000, ISBN 3-8274-0439-8.

[4] Bronstein, Semendjajew: Taschenbuch der Mathematik, Teubner-Verlag, Leipzig, 1979, ISBN 3 87144 492 8, S. 606

[5] Komplexe Mannigfaltigkeit. In: Guido Walz (Hrsg.): Lexikon der Mathematik. 1. Auflage. Spektrum Akademischer Verlag, Mannheim/Heidelberg 2000, ISBN 3-8274-0439-8.

[6] John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218). Springer-Verlag, New York NY u. a. 2003, ISBN 0-387-95448-1, S. 4ff.