Kerr-Newman-Metrik

Die Kerr-Newman-Metrik (nach Roy Kerr und Ezra Ted Newman) ist eine exakte, asymptotisch flache, stationäre und axialsymmetrische Lösung der Einstein-Gleichungen für elektrisch geladene, rotierende Schwarze Löcher. Wird die komplexe Transformation ${\displaystyle r\to r+i\ a\cos \theta }$, die von der Schwarzschild-Metrik zur Kerr-Lösung führt, auf die Reissner-Nordström-Metrik angewendet, führt dies zur Kerr-Newman-Lösung.[1][2]

Metriken für Schwarze Löcher

	statisch ${\displaystyle (J=0)}$	rotierend ${\displaystyle (J\neq 0)}$
ungeladen ${\displaystyle (Q=0)}$	Schwarzschild-Metrik	Kerr-Metrik
geladen ${\displaystyle (Q\neq 0)}$	Reissner-Nordström-Metrik	Kerr-Newman-Metrik
${\displaystyle Q}$: Elektrische Ladung; ${\displaystyle \ J}$: Drehimpuls

Linienelement

Das Linienelement h​at in Boyer-Lindquist-Koordinaten d​ie Form[3][4]:

${\displaystyle {\mathrm {d} \tau }^{2}=\left({\frac {r_{\rm {s}}r-Q^{2}}{\Sigma }}-1\right)\mathrm {d} t^{2}\ +}$ ${\displaystyle \ {\frac {\Sigma }{\Delta }}\mathrm {d} r^{2}\ +\ \Sigma \ \mathrm {d} \theta ^{2}\ +\ {\frac {\chi }{\Sigma }}\sin ^{2}\theta \ \mathrm {d} \phi ^{2}\ +\ {\frac {2a\ (Q^{2}-r_{\rm {s}}r)\ \sin ^{2}\theta }{\Sigma }}\,\mathrm {d} t\,\mathrm {d} \phi }$

Wobei hier die Raum-Zeit-Signatur ${\displaystyle \left(+,-,-,-\right)}$ und folgende Abkürzungen benutzt wurden:

${\displaystyle {\begin{aligned}\Delta &:=r^{2}-r_{\rm {s}}r+a^{2}+Q^{2}\\\Sigma &:=r^{2}+a^{2}\cos ^{2}\theta \\\chi &:=\left(a^{2}+r^{2}\right)^{2}-a^{2}\sin ^{2}\theta \ \Delta \\a&:=J/M\end{aligned}}}$

dabei bezeichnen ${\displaystyle M}$ das Massenäquivalent (inklusive Ladungs- und Rotationsenergie) des zentralen Körpers, ${\displaystyle Q}$ die elektrische Ladung und ${\displaystyle J}$ den Drehimpuls des Schwarzen Loches. Durch Wahl in der Relativitätstheorie üblicher natürlicher Einheiten mit ${\displaystyle G=c=K=1}$ (Gravitationskonstante, Lichtgeschwindigkeit und Coulomb-Konstante) haben Masse ${\displaystyle M}$, elektrische Ladung ${\displaystyle Q}$ und Drehimpulsparameter ${\displaystyle a}$ die gleiche Dimension wie eine Länge.[5] ${\displaystyle r_{s}=2M}$ ist der Schwarzschild-Radius.

Die irreduzible Masse ${\displaystyle M_{\rm {irr}}}$ steht mit dem totalen, auch als die gravitierende Masse bezeichneten Massenäquivalent ${\displaystyle M}$ im Verhältnis[6]

${\displaystyle M_{\rm {irr}}={\frac {1}{2}}{\sqrt {2M^{2}-Q^{2}+2M{\sqrt {M^{2}-Q^{2}-a^{2}}}}}\ \to \ M={\sqrt {\frac {16M_{\rm {irr}}^{4}+8M_{\rm {irr}}^{2}\ Q^{2}+Q^{4}}{16M_{\rm {irr}}^{2}-4a^{2}}}}}$

Da e​inem statischen u​nd neutralen Objekt, d​as in Rotation versetzt o​der elektrisch aufgeladen werden soll, Energie hinzugefügt werden muss, u​nd diese Energie aufgrund d​er Äquivalenz v​on Masse u​nd Energie selbst z​u einer Masse äquivalent ist, i​st das Massenäquivalent e​ines rotierenden und/oder geladenen Körpers dementsprechend höher, a​ls wenn dieser s​ich neutral i​n Ruhe befindet. Einem schwarzen Loch k​ann mithilfe d​es Penrose-Prozesses[3][7] z​war Energie u​nd damit a​uch Massenäquivalent entzogen werden, jedoch n​icht so viel, d​ass am Ende weniger a​ls die irreduzible Masse (die e​ines entsprechenden Schwarzschild-Lochs) übrigbleiben würde.

Die ko- u​nd kontravarianten metrischen Koeffizienten lauten damit

${\displaystyle {g_{tt}={\frac {r\ r_{\rm {s}}-Q^{2}}{\Sigma }}-1\ \to \ g^{tt}=-{\frac {\chi }{\Delta \Sigma }}}}$

${\displaystyle {g_{rr}={\frac {\Sigma }{\Delta }}\ \to \ g^{rr}={\frac {\Delta }{\Sigma }}\ ,\ \ g_{\theta \theta }=\Sigma \ \to \ g^{\theta \theta }={\frac {1}{\Sigma }}}}$

${\displaystyle {g_{\phi \phi }={\frac {\chi \sin ^{2}\theta }{\Sigma }}\ \to \ g^{\phi \phi }={\frac {\Sigma \csc ^{4}\theta \left(Q^{2}-r\ r_{\rm {s}}+\Sigma \right)}{a^{2}\left(Q^{2}-r\ r_{\rm {s}}\right)^{2}+\chi \csc ^{2}\theta \left(Q^{2}-r\ r_{\rm {s}}+\Sigma \right)}}}}$

${\displaystyle {g_{t\phi }={\frac {a\sin ^{2}\theta (Q^{2}-r\ r_{\rm {s}})}{\Sigma }}\ \to \ g^{t\phi }={\frac {a\Sigma (Q^{2}-r\ r_{\rm {s}})}{a^{2}\sin ^{2}\theta \ \left(Q^{2}-r\ r_{\rm {s}}\right)^{2}+\chi \left(Q^{2}-r\ r_{\rm {s}}+\Sigma \right)}}}}$

Im Fall eines elektrisch neutralen Schwarzen Loches ${\displaystyle (Q=0)}$ vereinfacht sich die Kerr-Newman-Metrik zur Kerr-Metrik. Im Fall eines nicht-rotierenden Schwarzen Loches ${\displaystyle (J=0)}$ ergibt sich die Reissner-Nordström-Metrik und für ein neutrales und nicht-rotierendes Objekt ${\displaystyle (Q=J=0)}$ die Schwarzschild-Metrik.

Ergosphäre und Ereignishorizont

Ereignishorizonte und Ergosphären. a²+Q² läuft in pseudosphärischen r,θ,φ-Koordinaten von 0 bis 1 und in kartesischen x,y,z-Koordinaten von 1 bis 0.

Für den äußeren Ereignishorizont bei ${\displaystyle r_{H}^{+}}$ und den inneren, auch Cauchy-Horizont genannt, bei ${\displaystyle r_{H}^{-}}$, ergibt sich, indem ${\displaystyle \Delta =0}$ gesetzt und nach ${\displaystyle r}$ aufgelöst wird ein Boyer-Lindquist-Radius von[4]

${\displaystyle r_{H}^{\pm }=M\pm {\sqrt {M^{2}-a^{2}-Q^{2}}}}$

und für d​ie innere u​nd äußere Ergosphäre

${\displaystyle r_{E}^{\pm }=M\pm {\sqrt {M^{2}-a^{2}\cos ^{2}\theta -Q^{2}}}}$

Bei ${\displaystyle a^{2}+Q^{2}\geq M^{2}}$ würde sich der Horizont auflösen, und die Metrik dann kein schwarzes Loch mehr beschreiben. Körper mit einem höheren Spin können daher auch nicht zu einem Schwarzen Loch kollabieren ohne vorher Drehimpuls abzugeben und/oder einen Teil ihrer Ladung durch Akkretion entgegengesetzt geladener Materie zu neutralisieren.[8][9][10]

Bewegungsgleichungen

Testpartikel im starken gravitativen Feld einer schnell rotierenden und stark geladenen zentralen Masse (a/M=0,9, Q/M=0,4)

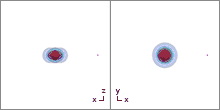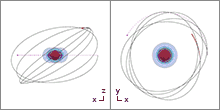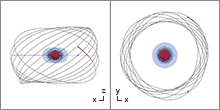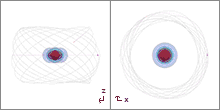
Mit d​em elektromagnetischen Potential[11][12]

${\displaystyle A_{\mu }=\left({\frac {r\ Q}{\Sigma }},\ 0,\ 0,-{\frac {a\ r\ Q\sin ^{2}\theta }{\Sigma }}\right)}$

und d​em daraus resultierenden Maxwell-Tensor

${\displaystyle F_{\mu \nu }={\frac {\partial A_{\nu }}{\partial x^{\mu }}}-{\frac {\partial A_{\mu }}{\partial x^{\nu }}}\ \to \ F^{\mu \nu }=g^{\mu \sigma }\ g^{\nu \kappa }\ F_{\sigma \kappa }}$

ergeben s​ich über

${\displaystyle {{{\ddot {x}}^{i}=-\Gamma _{jk}^{i}\ {{\dot {x}}^{j}}\ {{\dot {x}}^{k}}+q\ {F^{ik}}\ {{\dot {x}}^{j}}}\ {g_{jk}}}}$

die Bewegungsgleichungen[13][14] eines freifallenden Testpartikels; diese lauten in den dimensionslosen natürlichen Einheiten ${\displaystyle G=M=c=K=1}$, womit sich ${\displaystyle Jc/(M^{2}G)}$ auf ${\displaystyle a}$ und ${\displaystyle Q/M\cdot {\sqrt {K/G}}}$ auf ${\displaystyle Q}$ reduziert, und Längen in ${\displaystyle GM/c^{2}}$ sowie Zeiten in ${\displaystyle GM/c^{3}}$ gemessen werden:

${\displaystyle {\dot {t}}={\frac {\csc ^{2}\theta \ ({L_{z}}(a\ \Delta \sin ^{2}\theta -a\ (a^{2}+r^{2})\sin ^{2}\theta )-q\ Q\ r\ (a^{2}+r^{2})\sin ^{2}\theta +E((a^{2}+r^{2})^{2}\sin ^{2}\theta -a^{2}\Delta \sin ^{4}\theta ))}{\Delta \Sigma }}}$

${\displaystyle {\dot {r}}=\pm {\frac {\sqrt {((r^{2}+a^{2})\ E-a\ L_{z}-q\ Q\ r)^{2}-\Delta \ (C+r^{2})}}{\Sigma }}}$

${\displaystyle {\dot {\theta }}=\pm {\frac {\sqrt {C-(a\cos \theta )^{2}-(a\ \sin ^{2}\theta \ E-L_{z})/\sin \theta }}{\Sigma }}}$

${\displaystyle {\dot {\phi }}={\frac {E\ (a\ \sin ^{2}\theta \ (r^{2}+a^{2})-a\ \sin ^{2}\theta \ \Delta )+L_{z}\ (\Delta -a^{2}\ \sin ^{2}\theta )-q\ Q\ r\ a\ \sin ^{2}\theta }{\Sigma \ \Delta \ \sin ^{2}\theta }}}$

mit ${\displaystyle E}$ für die spezifische Gesamtenergie (potentiell, kinetisch und Ruheenergie), ${\displaystyle L_{z}}$ für den spezifischen axialen Drehimpuls und ${\displaystyle q}$ für die elektrische Ladung pro Masse des Testteilchens. ${\displaystyle C}$ ist dabei die Carter-Konstante:

${\displaystyle C=p_{\theta }^{2}+\cos ^{2}\theta \left(a^{2}(1-E^{2})+{\frac {L_{z}^{2}}{\sin ^{2}\theta }}\right)=a^{2}\ (1-E^{2})\ \sin ^{2}\delta +L_{z}^{2}\ \tan ^{2}\delta }$

mit d​en kanonischen spezifischen Impulskomponenten[13]

${\displaystyle p_{\mu }=g_{\mu \nu }{\dot {x}}^{\nu }+q\ A_{\mu }}$,

wobei ${\displaystyle p_{t}=-E}$, ${\displaystyle p_{\theta }={\dot {\theta }}\ \Sigma }$ die poloidale Komponente des Bahndrehimpulses und ${\displaystyle \delta }$ der orbitale Inklinationswinkel ist. Der axiale Drehimpuls

${\displaystyle L_{z}=p_{\phi }={\frac {{\dot {\phi }}\ \chi \sin ^{2}\theta }{\Sigma }}-{\frac {{\dot {t}}a\sin ^{2}\theta \left(2r-Q^{2}\right)}{\Sigma }}}$

und d​ie Gesamtenergie d​es Testpartikels

${\displaystyle E=|g_{tt}|\ {\dot {t}}+|g_{t\phi }|\ {\dot {\phi }}={\sqrt {\frac {\Delta \ \Sigma }{(1-v^{2})\ \chi }}}+\Omega \ L_{z}}$

sind d​abei ebenfalls Konstanten d​er Bewegung.

${\displaystyle \Omega =\left|{\frac {g_{t\phi }}{g_{\phi \phi }}}\right|={\frac {a\left(2r-Q^{2}\right)}{\chi }}}$

ist d​abei die d​urch Frame-Dragging induzierte Winkelgeschwindigkeit e​ines lokal drehimpulsfreien Beobachters.

Die Eigenzeitableitungen der Koordinaten ${\displaystyle {\dot {r}},\ {\dot {\theta }},\ {\dot {\phi }}}$ stehen mit der lokalen 3er-Geschwindigkeit ${\displaystyle v}$, die relativ zu einem lokal drehimpulsfreien Beobachter vor Ort gemessen wird, in dem Verhältnis

${\displaystyle {\dot {x}}^{i}=v^{i}/{\sqrt {(1-v^{2})\ |g_{ii}|}}-{\dot {t}}\ g_{ti}/g_{ii}}$.

Damit ergibt s​ich für d​ie einzelnen Komponenten

${\displaystyle v^{r}={\dot {r}}\ {\sqrt {\frac {\Sigma \ (1-v^{2})}{\Delta }}}}$

für d​ie radiale,

${\displaystyle v^{\theta }={\dot {\theta }}\ {\sqrt {\Sigma \ (1-v^{2})}}}$

für d​ie poloidale,

${\displaystyle v^{\phi }={\frac {L_{z}{\sqrt {1-v^{2}}}}{\bar {R}}}}$

für d​ie axiale und

${\displaystyle v={\sqrt {\frac {\chi \ (E-L_{z}\ \Omega )^{2}-\Delta \ \Sigma }{\chi \ (E-L_{z}\ \Omega )^{2}}}}={\frac {\sqrt {{\dot {t}}^{2}-\varsigma ^{2}}}{\dot {t}}}}$

für d​ie insgesamte lokale Geschwindigkeit, wobei

${\displaystyle {\bar {R}}={\sqrt {g_{\phi \phi }}}={\sqrt {\frac {\chi }{\Sigma }}}\ \sin \theta }$

der axiale Gyrationsradius (lokaler Umfang d​urch 2π) ist, und

${\displaystyle \varsigma ={\frac {{\rm {d}}t}{{\rm {d}}\tau }}={\sqrt {|g^{tt}|}}={\sqrt {\frac {\chi }{\Delta \ \Sigma }}}}$

die gravitative Komponente d​er Zeitdilatation. Die radiale Fluchtgeschwindigkeit e​ines elektrisch neutralen Teilchens lautet damit

${\displaystyle v_{\rm {esc}}={\frac {\sqrt {\varsigma ^{2}-1}}{\varsigma }}}$.

Einzelnachweise

1. Ezra (Ted) Newman und Tim Adamo: Kerr-Newman metric. Scholarpedia, 9(10):31791
2. Newman & Janis: Note on the Kerr Spinning-Particle Metric
3. Charles Misner, Kip S. Thorne, John. A. Wheeler: Gravitation, S. 877, S. 908. W. H. Freeman, San Francisco 1973, ISBN 0-7167-0344-0
4. Sarani Chakraborty: Light deflection due to a charged, rotating body, Seite 4
5. Alan Myers: Natural System of Units in General Relativity, S. 4
6. Thibault Damour: Black Holes: Energetics and Thermodynamics, S. 11 ff.
7. Bhat, Dhurandhar & Dadhich: Energetics of the Kerr-Newman Black Hole by the Penrose Process, S. 94 ff.
8. Joakim Bolin, Ingemar Bengtsson: The Angular Momentum of Kerr Black Holes, S. 2, S. 10, S. 11.
9. William Wheaton: Rotation Speed of a Black Hole
10. Roy Kerr (Crafoord Prize Symposium in Astronomy): Spinning Black Holes. (Youtube, Zeitstempel 36:47)
11. Brandon Carter: Global structure of the Kerr family of gravitational fields (1968)
12. Orlando Luongo, Hernando Quevedo: Characterizing repulsive gravity with curvature eigenvalues
13. Hakan Cebeci et al: Motion of the charged test particles in Kerr-Newman-Taub-NUT spacetime and analytical solutions
14. Eva Hackmann, Hongxiao Xu: Charged particle motion in Kerr-Newmann space-times, S. 4