Dyadisches Produkt
Das dyadische Produkt (kurz auch Dyade von griech. δύας, dýas „Zweiheit“) oder tensorielle Produkt ist in der Mathematik ein spezielles Produkt zweier Vektoren. Das Ergebnis eines dyadischen Produkts ist eine Matrix (oder ein Tensor zweiter Stufe) mit dem Rang eins. Das dyadische Produkt kann als Spezialfall eines Matrizenprodukts einer einspaltigen Matrix mit einer einzeiligen Matrix angesehen werden; es entspricht dann dem Kronecker-Produkt dieser beiden Matrizen. Um den Gegensatz zum inneren Produkt (Skalarprodukt) zu betonen, wird das dyadische Produkt gelegentlich auch äußeres Produkt genannt, wobei diese Bezeichnung aber nicht eindeutig ist, da sie auch für das Kreuzprodukt und das Dachprodukt verwendet wird.
Das Konzept des dyadischen Produkts geht auf den US-amerikanischen Physiker Josiah Willard Gibbs zurück, der es erstmals im Jahr 1881 im Rahmen seiner Vektoranalysis formulierte.[1]
Definition
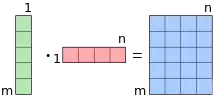
Das dyadische Produkt ist eine Verknüpfung zweier reeller Vektoren und der Form
- ,
wobei das Ergebnis eine Matrix ist. Jeder Eintrag der Ergebnismatrix berechnet sich dabei aus den Vektoren und über
als das Produkt der Elemente und . Interpretiert man den ersten Vektor als einspaltige Matrix und den zweiten Vektor als einzeilige Matrix, so lässt sich das dyadische Produkt mittels
als Matrizenprodukt darstellen, wobei der zu transponierte Vektor ist. Das dyadische Produkt kann so auch als Spezialfall des Kronecker-Produkts einer einspaltigen mit einer einzeiligen Matrix angesehen werden.
Beispiele
Sind und , dann ist das dyadische Produkt von und
Jede Spalte dieser Matrix ist also ein Vielfaches von und jede Zeile ein Vielfaches von . Als triviale Beispiele sind jede Nullmatrix das dyadische Produkt von Nullvektoren und jede Einsmatrix das dyadische Produkt von Einsvektoren entsprechend passender Größe:
- und
Eigenschaften
Die folgenden Eigenschaften des dyadischen Produkts ergeben sich direkt aus den Eigenschaften der Matrizenmultiplikation.
Kommutativität
Das dyadische Produkt ist, wie zahlreiche Beispiele belegen, nicht kommutativ.
Für die Transponierte des dyadischen Produkts zweier Vektoren und gilt
- .
Zwei Vektoren und sind damit genau dann vertauschbar, das heißt, es gilt
- ,
wenn die Ergebnismatrix symmetrisch ist. Dies ist genau dann der Fall, wenn einer der beiden Vektoren ein Vielfaches des anderen Vektors ist, das heißt, wenn es eine Zahl gibt, sodass oder gilt. Ist einer der Vektoren ein Nullvektor, dann gilt insbesondere für alle
- ,
wobei die Ergebnismatrix dann die Nullmatrix ist.
Distributivität
Mit der Vektoraddition ist das dyadische Produkt distributiv, das heißt, es gilt für alle und
sowie für alle und entsprechend
- .
Weiter ist das dyadische Produkt verträglich mit der Skalarmultiplikation, das heißt für und sowie gilt
- .
Dyadisches Produkt zweier Vektoren
Das dyadische Produkt zweier Vektoren und ergibt, sofern keiner der beiden Vektoren der Nullvektor ist, eine Rang-Eins-Matrix, das heißt
- .
Umgekehrt lässt sich jede Rang-Eins-Matrix als dyadisches Produkt zweier Vektoren darstellen. Für die Spektralnorm und die Frobeniusnorm eines dyadischen Produkts gilt
- ,
wobei die euklidische Norm des Vektors ist. Neben der Nullmatrix sind Rang-Eins-Matrizen die einzigen Matrizen, für die diese beiden Normen übereinstimmen.
Bezüge zu anderen Produkten
Skalarprodukt
Bildet man umgekehrt das Produkt aus einem Zeilenvektor mit einem Spaltenvektor, so erhält man das Standardskalarprodukt zweier Vektoren gegeben durch
- ,
wobei das Ergebnis eine reelle Zahl ist. Das Standardskalarprodukt zweier Vektoren ist gleich der Spur (der Summe der Diagonalelemente) ihres dyadischen Produkts, also
- .
Weiter ist die Matrix genau dann nilpotent (immer vom Grad 2), wenn die beiden Vektoren orthogonal sind, das heißt
- .
Wenn sich Zeilen- und Spaltenvektoren passender Größe abwechseln, können auch mehrere Vektoren miteinander multipliziert werden. Aufgrund der Assoziativität der Matrizenmultiplikation erhält man so die Identitäten
und
- .
Ein Skalarprodukt wird auch inneres Produkt genannt, weswegen das dyadische Produkt gelegentlich auch als äußeres Produkt bezeichnet wird. Diese Dualität wird in der Bra-Ket-Notation der Quantenmechanik genutzt, wo ein inneres Produkt durch und ein äußeres Produkt durch notiert wird.
Tensorprodukt
Der Vektorraum, der durch dyadische Produkte von Vektoren aufgespannt wird, ist der Tensorproduktraum
- .
Dieser Raum ist isomorph zum Raum aller Matrizen . Jede Matrix lässt sich demnach als Linearkombination dyadischer Produkte von Vektoren darstellen, das heißt
- ,
wobei , und sind. Durch eine geeignete Wahl von Vektoren und einer Rangschranke lässt sich auf diese Weise auch eine Niedrigrang-Approximation einer Matrix erreichen, wodurch numerische Berechnungen bei sehr großen Matrizen beschleunigt werden können.[2]
Verwendung
In vielen Anwendungen wird ein dyadisches Produkt nicht komponentenweise ausgerechnet, sondern zunächst stehen gelassen und erst ausgewertet, wenn es mit weiteren Termen multipliziert wird. Multipliziert man das dyadische Produkt mit einem Vektor , erhält man einen Vektor, der parallel zu ist, da
gilt. Das dyadische Produkt eines Einheitsvektors mit sich selbst ist ein Projektionsoperator, denn das Matrix-Vektor-Produkt
projiziert einen gegebenen Vektor orthogonal auf eine Ursprungsgerade mit Richtungsvektor . Die Spiegelung eines Vektors an einer Ursprungsebene mit Einheits-Normalenvektor ergibt sich entsprechend als
- ,
wobei die Einheitsmatrix ist. Solche Spiegelungen werden beispielsweise in der Householdertransformation verwendet.
In der digitalen Bildverarbeitung können Faltungsmatrizen als dyadisches Produkt zweier Vektoren dargestellt werden. Durch diese Separierbarkeit können z. B. Weichzeichnungs- oder Kantenerkennungsfilter in „two passes“ (engl. zwei Durchläufe) angewendet werden, um den Rechenaufwand zu reduzieren.
Als Beispiel der 5 × 5 „convolution kernel“ (engl. Faltungsmatrix) des Gaußschen Weichzeichners:
Koordinatenfreie Darstellung
In einer abstrakteren, koordinatenfreien Darstellung ist das dyadische Produkt zweier Vektoren und aus zwei Vektorräumen und ein Tensor zweiter Stufe im Tensorproduktraum . Die verschiedenen Notationen verwenden teilweise Fettdruck für Vektoren oder lassen das Zeichen weg:
Nicht jeder Tensor zweiter Stufe ist ein dyadisches Produkt von zwei Vektoren, jedoch kann jeder Tensor zweiter Stufe als Summe dyadischer Produkte dargestellt werden. Ein Tensor, der dyadisches Produkt zweier Vektoren ist, heißt einfacher Tensor oder Dyade.
Anwendung findet diese Version des dyadischen Produkts in der Kontinuumsmechanik, wo meist identisch mit dem dreidimensionalen Vektorraum der geometrischen Vektoren ist.
Ist ein euklidischer Vektorraum, so kann mit Hilfe des Skalarprodukts „·“ von das innere Produkt zwischen Tensoren und Vektoren definiert werden. Es ordnet jedem Tensor und Vektoren einen Vektor zu. Für Dyaden ist das innere Produkt wie folgt definiert:
Hierdurch kann jede Dyade und damit auch jeder Tensor als lineare Abbildung
aufgefasst werden. Der Tensorproduktraum kann also mit dem Raum der linearen Abbildungen von nach identifiziert werden. Dies wird im Folgenden getan.
Für das dyadische Produkt gelten die folgenden Rechenregeln. , , und , seien euklidische Vektorräume. Dann gilt für alle :
- .
Zu beachten ist hier, dass die Skalarprodukte „·“ in den Gleichungen aus den verschiedenen Vektorräumen stammen, was sich durch einen Index verdeutlicht beispielsweise wie folgt schreibt: .
Das Skalarprodukt zweier Tensoren aus kann mit Vektoren definiert werden:
Damit baut einen euklidischen Vektorraum auf, dessen Elemente Tensoren zweiter Stufe sind. Mit einer Basis von und von besitzt eine Basis bezüglich der jeder Tensor komponentenweise dargestellt werden kann:
worin die Dimension von und die Dimension von ist. Der Tensor ist von den verwendeten Basen unabhängig. Bei einem Basiswechsel ändern sich daher die Komponenten auf charakteristische Weise. Von Bedeutung sind Invarianten, die bei solchen Basiswechseln ihren Wert nicht ändern, siehe z. B. Hauptinvariante.
Die Komponenten können in einer Matrix angeordnet werden, wobei dann die verwendete Basis in Erinnerung behalten werden muss. Gelegentlich wird z. B.
geschrieben. Ist der Definitionsbereich mit dem Bildbereich identisch, kann bei Verwendung der Standardbasis der Verweis auf die verwendete Basis weggelassen werden und der Tensor geht in seine Matrixrepräsentation über, z. B.:
- .
In Koordinatendarstellung ist das oben als Matrix definierte dyadische Produkt zweier Spaltenvektoren gerade diese Abbildungsmatrix des Tensors.
Literatur
- Gerd Fischer: Lineare Algebra. 14. Auflage. Vieweg, 2003, ISBN 3-528-03217-0.
- Rudolf Zurmühl: Matrizen und ihre Anwendungen. 7. Auflage. Springer, 1997, ISBN 3-540-61436-2.
- Hans Karl Iben: Tensorrechnung. 2. Auflage. Teubner, 1999, ISBN 3-519-00246-9.
- H. Altenbach: Kontinuumsmechanik. Springer Verlag, 2012, ISBN 978-3-642-24118-5.
- Peter Haupt: Continuum Mechanics and Theory of Materials. Springer, Berlin u. a. 2000, ISBN 3-540-66114-X.
Einzelnachweise
- Ari Ben-Menahem: Historical Encyclopedia of Natural and Mathematical Sciences. Band 1. Springer, 2009, ISBN 978-3-540-68831-0, S. 2463.
- Ivan Markovsky: Low Rank Approximation. Algorithms, Implementation, Applications. Springer, 2011, ISBN 978-1-4471-2227-2.
Weblinks
- Eric W. Weisstein: Vector Direct Product. In: MathWorld (englisch).
- pahio: Dyad Product. In: PlanetMath. (englisch)