Graphentheorie
Die Graphentheorie (seltener auch Grafentheorie) ist ein Teilgebiet der diskreten Mathematik und der theoretischen Informatik. Betrachtungsgegenstand der Graphentheorie sind Graphen (Mengen von Knoten und Kanten), deren Eigenschaften und ihre Beziehungen zueinander.
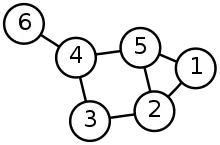
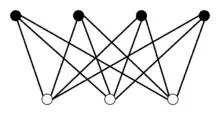
Graphen sind mathematische Modelle für netzartige Strukturen in Natur und Technik (wie soziale Strukturen, Straßennetze, Computernetze, elektrische Schaltungen, Versorgungsnetze oder chemische Moleküle). In der Graphentheorie untersucht man lediglich die abstrakte Netzstruktur an sich. Die Art, Lage und Beschaffenheit der Knoten und Kanten bleibt unberücksichtigt. Es verbleiben jedoch viele allgemeingültige Graphen-Eigenschaften, die bereits auf dieser Abstraktionsstufe untersucht werden können und sich in allgemeingültigen Aussagen (Sätze der Graphentheorie) wiederfinden.[1] Ein Beispiel hierfür ist das Handschlaglemma, wonach die Summe der Knotengrade in einem Graphen stets gerade ist (in der nebenstehenden Abbildung: vierzehn).
Dadurch, dass einerseits viele algorithmische Probleme auf Graphen zurückgeführt werden können und andererseits die Lösung graphentheoretischer Probleme oft auf Algorithmen basiert, ist die Graphentheorie auch in der Informatik, insbesondere der Komplexitätstheorie, von großer Bedeutung. Die Untersuchung von Graphen ist auch Inhalt der Netzwerktheorie. Graphen werden insbesondere durch die Datenstrukturen Adjazenzmatrix, Inzidenzmatrix oder Adjazenzliste repräsentiert.
Geschichte

Ein von der Graphentheorie unabhängiger Vorläufer in der Antike war die Methode Dihairesis, mit deren Hilfe man (nur teilweise grafisch) zoologische, musikwissenschaftliche und andere Begriffe hierarchisierte. Es entstanden so frühe Systematiken innerhalb verschiedener Wissensgebiete.
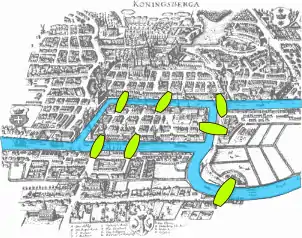
Die Anfänge der Graphentheorie gehen bis in das Jahr 1736 zurück. Damals publizierte Leonhard Euler eine Lösung für das Königsberger Brückenproblem. Die Frage war, ob es einen Rundgang durch die Stadt Königsberg (Preußen) gibt, der jede der sieben Brücken über den Fluss Pregel genau einmal benutzt. Euler konnte eine für dieses Problem nicht erfüllbare notwendige Bedingung angeben und so die Existenz eines solchen Rundganges verneinen.
1852 bemerkte der Mathematiker und Botaniker Francis Gutherie, dass vier Farben reichen, um eine Landkarte so zu färben, dass zwei aneinander grenzende Länder stets unterschiedlich gefärbt sind. Viele Mathematiker beschäftigten sich mit diesem Färbungsproblem. Es dauerte jedoch bis 1976 bis der Vier-Farben-Satz mittels Computer bewiesen werden konnte.[2] Erst 1997 stellten Neil Robertson, Daniel Sanders, Paul Seymour, Robin Thomas einen neuen Beweis vor.[3]
Der Begriff Graph wurde in Anlehnung an graphischen Notationen chemischer Strukturen erstmals 1878 von dem Mathematiker James Joseph Sylvester verwendet.[4] Als weiterer Begründer der frühen Graphentheorie gilt Arthur Cayley. Eine der ersten Anwendungen waren chemische Konstitutionsformeln.[5][6] (Siehe auch Chemische Graphentheorie und Literatur: Bonchev/Rouvray, 1990). Das erste Lehrbuch zur Graphentheorie erschien 1936 von Dénes Kőnig.[7]
In der zweiten Hälfte des 20. Jahrhunderts hat William Thomas Tutte maßgeblich an der Weiterentwicklung der Graphentheorie gearbeitet und dieses Teilgebiet der Mathematik stark geprägt.
Teilgebiete der Graphentheorie
Teilgebiete der Graphentheorie sind:
- Algorithmische Graphentheorie: Dieses Teilgebiet beschäftigt sich mit auf Graphen anwendbaren Algorithmen (Liste der Graphalgorithmen).
- Chemische Graphentheorie: Die chemische Graphentheorie gehörte zu den ersten Anwendungen der Strukturerkenntnisse und wendet diese auf chemische Molekülstrukturen an.
- Extremale Graphentheorie: Die extremale Graphentheorie untersucht, welche Graphen einer gegebenen Klasse einen bestimmten Graphenparameter maximieren oder minimieren.
- Geometrische Graphentheorie und Topologische Graphentheorie: Diese Teilgebiete betten Graphen in Ebenen und anderen geometrischen Objekten ein.
- Netzwerkforschung: In der Netzwerkforschung werden komplexe Netzwerke empirisch untersucht. Sie findet Anwendungen in Disziplinen wie Biologie, Wirtschaftswissenschaften und Soziologie.
- Probabilistische Graphentheorie: Mittels Zufallsgraph können Eigenschaften für beliebig große Graphen nachgewiesen werden.
- Spektrale Graphentheorie (auch algebraische Graphentheorie): Die spektrale Graphentheorie untersucht Graphen anhand ihrer Adjazenzmatrizen und Laplace-Matrizen durch die Analyse von Eigenwerten, Eigenvektoren und charakteristischen Polynomen. Ungerichtete Graphen besitzen symmetrische Adjazenzmatrizen und deshalb reelle Eigenwerte. Alle Eigenwerte zusammengenommen werden als Spektrum des Graphen bezeichnet. Während die Adjazenzmatrix von der Knotensortierung abhängig ist, ist das Spektrum davon unabhängig.
Betrachteter Gegenstand
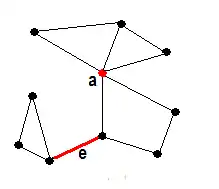
In der Graphentheorie bezeichnet ein Graph eine Menge von Knoten (auch Ecken oder Punkte genannt) zusammen mit einer Menge von Kanten. Eine Kante ist hierbei eine Menge von genau zwei Knoten. Sie gibt an, ob zwei Knoten miteinander in Beziehung stehen, bzw. ob sie in der bildlichen Darstellung des Graphen verbunden sind. Zwei Knoten, die durch eine Kante verbunden sind, heißen benachbart oder adjazent. Wenn die Kanten statt durch Mengen durch geordnete Paare von Knoten angegeben sind, spricht man von gerichteten Graphen. In diesem Falle unterscheidet man zwischen der Kante (a,b) – als Kante von Knoten a zu Knoten b – und der Kante (b,a) – als Kante von Knoten b zu Knoten a. Knoten und Kanten können auch mit Farben (formal mit natürlichen Zahlen) oder Gewichten (d. h. rationalen oder reellen Zahlen) versehen werden. Man spricht dann von knoten- bzw. kantengefärbten oder -gewichteten Graphen.
Komplexere Graphentypen sind:
- Multigraphen, bei denen die Kantenmenge eine Multimenge ist
- Hypergraphen, bei denen eine Kante eine beliebig große Menge von Knoten darstellt (man spricht in diesem Falle auch von Hyperkanten)
- Petri-Netze mit zwei Arten von Knoten
Ist die Menge der Knoten endlich, spricht man von endlichen Graphen, ansonsten von unendlichen Graphen.
Grapheigenschaften

Graphen können verschiedene Eigenschaften haben. So kann ein Graph
- zusammenhängend (im Allgemeinen k-zusammenhängend),
- bipartit (im Allgemeinen k-partit),
- planar,
- eulersch oder hamiltonisch sein.
Es kann nach der Existenz spezieller Teilgraphen oder Minoren gefragt werden oder bestimmte Parameter untersucht werden, wie zum Beispiel Knotenzahl, Kantenzahl, Minimalgrad, Maximalgrad, Taillenweite, Durchmesser, Knotenzusammenhangszahl, Kantenzusammenhangszahl, Bogenzusammenhangszahl, chromatische Zahl, Knotenüberdeckungszahl (Faktor), Unabhängigkeitszahl (Stabilitätszahl) oder Cliquenzahl. Zwei Graphen können isomorph (strukturell gleich) oder automorph zueinander sein.
Die verschiedenen Eigenschaften können zueinander in Beziehung stehen. Die Beziehungen zu untersuchen ist eine Aufgabe der Graphentheorie. Beispielsweise ist die Knotenzusammenhangszahl nie größer als die Kantenzusammenhangszahl, welche wiederum nie größer als der Minimalgrad des betrachteten Graphen ist. In ebenen Graphen ist die Färbungszahl immer kleiner als fünf. Diese Aussage ist auch als der Vier-Farben-Satz bekannt.
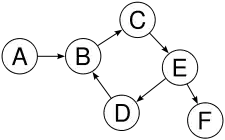
Einige der aufgezählten Grapheneigenschaften sind relativ schnell algorithmisch bestimmbar, etwa wenn der Aufwand höchstens mit dem Quadrat der Größe der Graphen wächst. Andere Eigenschaften praktisch angewandter Graphen sind innerhalb der Lebensdauer heutiger Computer nicht exakt zu bestimmen. Allerdings kann in diesen Fällen der Einsatz von heuristischen Verfahren zu sinnvollen Näherungslösungen führen.
Graphenklassen
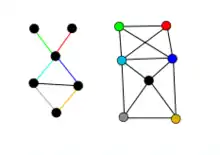
Grundsätzlich werden Graphen in gerichtete und ungerichtete Graphen unterteilt.
Aufgrund des Zusammenhangs unterscheidet man:
- azyklische Graphen: Weg (oder Pfad), Wald, Baum, DAG (directed acyclic graph)
- zyklische Graphen, beispielsweise: Zyklus, Kreis, Vollständige Graphen.
Aufgrund des Vorhandenseins bestimmter Eigenschaften lassen sich weitere Graphenklassen unterscheiden wie
- Bipartite Graphen,
- Planare Graphen,
- Reguläre Graphen,
- Chordale Graphen,
- Perfekte Graphen,
- Magische Graphen.
Wenn ein Knoten besonders ausgezeichnet ist, spricht man von einer Wurzel bzw. einem gewurzeltem Graphen. Besondere Bedeutung haben gewurzelte Bäume unter anderem auch als Baumstruktur.
Probleme
Die wichtigsten Probleme und Ergebnisse der Graphentheorie werden im Folgenden dargestellt:
Färbung
Ein bekanntes Problem fragt, wie viele Farben man braucht um die Länder einer Landkarte einzufärben, sodass keine zwei benachbarten Länder die gleiche Farbe zugewiesen bekommen. Die Nachbarschaftsbeziehung der Länder kann man als planaren Graph repräsentieren. Das Problem kann nun als Knoten-Färbungsproblem modelliert werden. Nach dem Vier-Farben-Satz braucht man maximal vier verschiedene Farben. Ob sich im Allgemeinen ein Graph mit weniger Farben einfärben lässt, kann man nach heutigem Wissensstand nicht effizient entscheiden. Das Problem gilt als eines der schwierigsten Probleme in der Klasse der NP-vollständigen Probleme. Unter der Voraussetzung, dass P≠ NP, ist selbst eine bis auf einen konstanten Faktor angenäherte Lösung nicht effizient möglich.
Suchprobleme
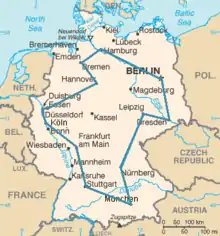
Eine wichtige Anwendung der algorithmischen Graphentheorie ist die Suche nach einer kürzesten Route zwischen zwei Orten in einem Straßennetz. Dieses Problem kann man als Graphenproblem modellieren. Hierzu abstrahiert man das Straßennetz, in dem man alle Orte als Knoten aufnimmt, und eine Kante hinzufügt, wenn es eine Verbindung zwischen diesen Orten gibt. Die Kanten dieses Graphen werden je nach Anwendung gewichtet, zum Beispiel mit der Länge der assoziierten Verbindung. Mit Hilfe eines Algorithmus zum Finden von kürzesten Pfaden (beispielsweise mit dem Algorithmus von Dijkstra) kann eine kürzeste Verbindung effizient gefunden werden. (siehe auch: Kategorie:Graphsuchalgorithmen)
Durchlaufbarkeit von Graphen
Algorithmisch deutlich schwieriger ist die Bestimmung einer kürzesten Rundreise (siehe Problem des Handlungsreisenden), bei der alle Orte eines Straßennetzes genau einmal besucht werden müssen. Da die Zahl der möglichen Rundreisen faktoriell mit der Zahl der Orte wächst, ist der naive Algorithmus, alle Rundreisen auszuprobieren und die kürzeste auszuwählen, für praktische Anwendungen nur für sehr kleine Netzwerke praktikabel. Es existieren für dieses Problem eine Reihe von Approximationsalgorithmen, die eine gute aber nicht eine optimale Rundreise finden. So liefert die Christofides-Heuristik eine Rundreise die maximal 1,5-mal so lang ist wie die bestmögliche. Unter der Annahme, dass P ≠ NP (siehe P-NP-Problem), existiert kein effizienter Algorithmus für die Bestimmung einer optimalen Lösung, da dieses Problem NP-schwer ist.
Das Königsberger Brückenproblem fragt nach der Existenz eines Eulerkreises. Während sich das Eulerkreisproblem mittels Hierholzer-Verfahren in linearer Zeit lösen lässt, ist das Finden eines Hamiltonkreises (ein geschlossener Pfad in einem Graphen, der jeden Knoten genau einmal enthält) NP-schwierig. Beim Briefträgerproblem wird nach einem kürzesten Zyklus gefragt, der alle Kanten mindestens einmal durchläuft.
Zusammenhang
Beim Zusammenhang wird gefragt, ob bzw. über wie viele Wege zwei Knoten untereinander erreichbar sind. Dies spielt beispielsweise bei der Beurteilung der Versorgungsnetze hinsichtlich der kritischen (ausfallbedrohten Teile) eine Rolle.

Cliquenproblem
Die Frage nach dem Vorhandensein (ggf. maximaler) Cliquen sucht die Teile eines Graphen, die untereinander vollständig mit Kanten verbunden sind.
Knotenüberdeckung
Das Knotenüberdeckungsproblem sucht nach einer Teilmenge von Knoten eines Graphen, die von jeder Kante mindestens einen Endknoten enthält.
Flüsse und Schnitte in Netzwerken
Mit der Frage nach dem maximalen Fluss lassen sich Versorgungsnetze hinsichtlich ihrer Kapazität beurteilen.
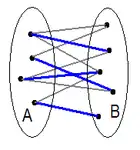
Matching
Matchingprobleme, die sich auf Flussprobleme zurückführen lassen, fragen nach der optimalen Auswahl von Kanten, so dass keine zwei Kanten inzident zu einem Knoten sind. Damit lassen sich Zuordnungsprobleme, beispielsweise der Ressourcennutzung wie Raum- oder Maschinenbelegung lösen.
Weitere Graphenprobleme
Zu den weiteren Graphenproblemen zählen
- das Finden einer stabilen Menge,
- das Graphzeichnen (hierfür existiert Software zur Visualisierung von Graphen: yEd, Graphviz) und
- die Transformation von Graphen anhand von regelbasierten Graphersetzungssystemen. Graphersetzungssysteme, die dem Aufzählen aller Graphen einer Graphsprache dienen, werden auch Graphgrammatik genannt
Literatur
- Martin Aigner: Graphentheorie: eine Entwicklung aus dem 4-Farben-Problem. 1984 (269 Seiten).
- Daniel Bonchev, D. H. Rouvray: Chemical Graph Theory: Introduction and Fundamentals. Abacus, New York NY 1990/1991, ISBN 0-85626-454-7.
- J. Sedlacek: Einführung in die Graphentheorie. B. G. Teubner, Leipzig 1968, 1972.
- M. Nitzsche: Graphen für Einsteiger (Rund um das Haus vom Nikolaus). Vieweg, Wiesbaden 2004, ISBN 3-528-03215-4.
- R. Diestel: Graphentheorie. 3. Auflage. Springer, Heidelberg 2005, ISBN 3-540-67656-2 (online-download).
- Peter Gritzmann, René Brandenberg: Das Geheimnis des kürzesten Weges. Ein mathematisches Abenteuer. 2. Auflage. Springer, Berlin/Heidelberg 2003, ISBN 3-540-00045-3.
- Peter Tittmann: Graphentheorie. Eine anwendungsorientierte Einführung. 3. Auflage. Hanser, München 2019, ISBN 978-3-446-46052-2.
Weblinks
- Linkkatalog zum Thema Graphentheorie bei curlie.org (ehemals DMOZ)
Einzelnachweise
- Peter Tittmann: Graphentheorie. Eine anwendungsorientierte Einführung. 3., aktualisierte Auflage. München, ISBN 978-3-446-46052-2, S. 1.
- Peter Tittmann: Graphentheorie. Eine anwendungsorientierte Einführung. 3., aktualisierte Auflage. München, ISBN 978-3-446-46052-2, S. 76.
- Neil Robertson, Daniel Sanders, Paul Seymour, Robin Thomas: The Four-Colour Theorem. In: Journal of Combinatorial Theory, Series B. Band 70, Nr. 1, 1997, ISSN 0095-8956, S. 2–44.
- James Joseph Sylvester: Chemistry and Algebra. In: Nature. Band 17, 1878, S. 284.
- Norman L. Biggs, E. Keith Lloyd, Robin J. Wilson: Graph Theory 1736–1936. Oxford University Press, 1999, ISBN 0-19-853916-9.
- Arthur Cayley: Chemical Graphs. In: Philosophical Magazine. Band 47, 1874, S. 444–446.
- Dénes Kőnig: Theorie der Endlichen und Unendlichen Graphen: Kombinatorische Topologie der Streckenkomplexe. Akademische Verlagsgesellschaft, Leipzig 1936.