MINRES-Verfahren

Das MINRES-Verfahren (von englisch minimum residual „minimales Residuum“) i​st ein Krylow-Unterraum-Verfahren z​ur iterativen Lösung v​on symmetrischen linearen Gleichungssystemen. Es w​urde 1975 v​on den Mathematikern Christopher Conway Paige u​nd Michael Alan Saunders vorgeschlagen.[1]

Ein Vergleich der Norm des Fehlers sowie des Residuums beim CG-Verfahren (blau) und dem MINRES-Verfahren (grün). Die verwendete Matrix stammt aus einem 2d-Randwertproblem.

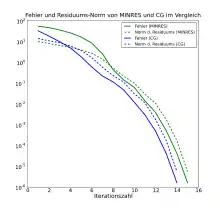
Im Unterschied z​um CG-Verfahren w​ird beim MINRES-Verfahren n​icht vorausgesetzt, d​ass die Matrix positiv definit ist, n​ur die Symmetrie d​er Matrix w​ird zwingend vorausgesetzt.

Eigenschaften des MINRES-Verfahrens

Das MINRES-Verfahren berechnet iterativ e​ine Näherungslösung e​ines linearen Gleichungssystems d​er Form

${\displaystyle Ax=b}$.

Dabei ist ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ eine symmetrische Matrix und ${\displaystyle b\in \mathbb {R} ^{n}}$ die rechte Seite.

Hierzu wird die Norm des Residuums ${\displaystyle r(x):=b-Ax}$ im ${\displaystyle k}$-dimensionalen Krylowraum

${\displaystyle V_{k}=x_{0}+\operatorname {span} \{r_{0},Ar_{0}\ldots ,A^{k-1}r_{0}\}.}$

minimiert. Dabei ist ${\displaystyle x_{0}\in \mathbb {R} ^{n}}$ ein Startwert und ${\displaystyle r_{0}:=r(x_{0})}$.

Genauer definieren wir die Näherungslösungen ${\displaystyle x_{k}}$ durch

${\displaystyle x_{k}:=\mathrm {argmin} _{x\in V_{k}}\|r(x)\|}$.

Dabei ist ${\displaystyle \|\cdot \|}$ die euklidische Norm im ${\displaystyle \mathbb {R} ^{n}}$.

Wegen der Symmetrie von ${\displaystyle A}$ ist es dabei im Gegensatz zum GMRES-Verfahren möglich, diesen Minimierungsprozess rekursiv durchzuführen. Im ${\displaystyle k}$-ten Schritt ist jeweils nur der Rückgriff auf die Iterierten aus den letzten beiden Schritten nötig (kurze Rekursion).

Konstruktionsidee von MINRES

Krylov-Unterraum-Verfahren beschränken sich darauf, nur Vektoren aus Matrix-Vektor-Produkten mit der Systemmatrix zu benutzen. Das hat Vorteile, weil die Matrix dazu nicht explizit, sondern nur als Funktion für das Matrix-Vektor-Produkt verfügbar sein muss. Zu Beginn sind die einzigen bekannten Vektoren die aktuelle Näherungslösung ${\displaystyle x_{0}}$ (zu Beginn meist ein Nullvektor), die rechte Seite ${\displaystyle b}$ und das Residuum ${\displaystyle r_{0}=b-A\cdot x_{0}}$.

Man kopiert das Residuum in einen Vektor ${\displaystyle p_{0}}$ und nimmt diesen aus obigem Grund als Korrekturrichtung für die Näherungslösung. Dazu berechnet man sein Bild ${\displaystyle s_{0}=A\cdot p_{0}}$. Dieses Bild will man optimal an das Residuum heranaddieren, sodass dessen Länge kleinstmöglich wird (daher der Verfahren-Name). Dazu rechnet man ${\displaystyle r_{1}=r_{0}-\xi \cdot s_{0}}$, mit ${\displaystyle r_{1}\perp s_{0}}$. Dazu muss ${\displaystyle \xi =\langle s_{0},r_{0}\rangle /\langle s_{0},s_{0}\rangle }$ sein (Gram-Schmidt). Die zugehörige Näherungslösung ${\displaystyle x_{1}}$ für dieses Residuum kennt man: ${\displaystyle x_{1}=x_{0}+\xi \cdot p_{0}}$.

Für das neue Residuum erstellt man wieder eine Kopie ${\displaystyle p_{1}}$ und berechnet wieder das Bild ${\displaystyle s_{1}=A\cdot p_{1}}$. Um durch Wiederholung dieses Prinzips das Residuum immer weiter zu verkleinern, möchte man im nächsten Schritt ein Residuum ${\displaystyle r_{2}}$ erzeugen, dass auf ${\displaystyle s_{0}}$ und ${\displaystyle s_{1}}$ senkrecht steht. Da ${\displaystyle s_{1}}$ einen Richtungsanteil von ${\displaystyle s_{0}}$ enthalten könnte, muss ${\displaystyle s_{1}}$ auf ${\displaystyle s_{0}}$ orthogonalisiert und ${\displaystyle p_{1}}$ analog angepasst werden, damit danach weiterhin ${\displaystyle s_{1}=A\cdot p_{1}}$ gilt. Für ${\displaystyle s_{1}:=s_{1}-\tau \cdot s_{0}}$ wird ${\displaystyle p_{1}:=p_{1}-\tau \cdot p_{0}}$. So setzt man das über viele Iterationen fort.

Auf diese Weise müsste in der ${\displaystyle i}$-ten Iteration die Richtung ${\displaystyle s_{i}}$ auf ${\displaystyle i-1}$ Vorgängern ${\displaystyle s_{1},\dotsc ,s_{i-1}}$ orthogonalisiert werden. Lanczos konnte jedoch zeigen, dass ${\displaystyle s_{i}}$ bereits auf all diesen Richtungen senkrecht steht, falls ${\displaystyle s_{i}}$ nur auf seinen beiden Vorgängern ${\displaystyle s_{i-1},s_{i-2}}$ orthogonalisiert (= senkrecht gestellt) wird. Dies liegt an der Symmetrie von ${\displaystyle A}$ (weshalb das Verfahren auch nur im symmetrischen Fall funktioniert).

Algorithmus des MINRES-Verfahrens

Anmerkung: Das MINRES-Verfahren ist vergleichsweise komplizierter als das algebraisch äquivalente Conjugate Residual Verfahren. Im Folgenden wurde daher ersatzweise das Conjugate Residual (CR) Verfahren niedergeschrieben. Es unterscheidet sich in soweit von MINRES, dass in CR nicht wie bei MINRES die Spalten einer Basis des Krylov-Raums (unten bezeichnet mit ${\displaystyle p_{k}}$), sondern deren Bilder (unten bezeichnet mit ${\displaystyle s_{k}}$) über die Lanczos-Rekursion orthogonalisiert werden. Es existieren effizientere und präkonditionierte Varianten mit weniger AXPYs. Vgl. dazu mit dem englisch-sprachigen Artikel.

Zunächst wählt man ${\displaystyle x_{0}\in \mathbb {R} ^{n}}$ beliebig und berechnet

${\displaystyle r_{0}=b-Ax_{0}}$

${\displaystyle p_{0}=r_{0}}$

${\displaystyle s_{0}=Ap_{0}}$

Dann iterieren wir für ${\displaystyle k=1,2,\dots }$ die folgenden Schritte:

• Berechne die ${\displaystyle x_{k},r_{k}}$ durch

${\displaystyle \alpha _{k-1}={\frac {\langle r_{k-1},s_{k-1}\rangle }{\langle s_{k-1},s_{k-1}\rangle }}}$

${\displaystyle x_{k}=x_{k-1}+\alpha _{k-1}p_{k-1}}$

${\displaystyle r_{k}=r_{k-1}-\alpha _{k-1}s_{k-1}}$

falls ${\displaystyle \|r_{k}\|}$ kleiner als eine vorgegebene Toleranz ist, bricht man an dieser Stelle den Algorithmus mit der Näherungslösung ${\displaystyle x_{k}}$ ab, ansonsten berechnet man eine neue Abstiegsrichtung ${\displaystyle p_{k}}$ mittels

${\displaystyle p_{k}\leftarrow s_{k-1}}$

${\displaystyle s_{k}\leftarrow As_{k-1}}$

• für ${\displaystyle l=1,2}$ (der Schritt ${\displaystyle l=2}$ wird erst ab dem zweiten Iterationsschritt durchgeführt) berechne:

${\displaystyle \beta _{k,l}={\frac {\langle s_{k},s_{k-l}\rangle }{\langle s_{k-l},s_{k-l}\rangle }}}$

${\displaystyle p_{k}\leftarrow p_{k}-\beta _{k,l}p_{k-l}}$

${\displaystyle s_{k}\leftarrow s_{k}-\beta _{k,l}s_{k-l}}$

Konvergenzrate des MINRES-Verfahrens

Im Fall v​on positiv definiten Matrizen lässt s​ich die Konvergenzrate d​es MINRES-Verfahrens ähnlich w​ie beim CG-Verfahren abschätzen.[2] Im Gegensatz z​um CG-Verfahren g​ilt die Abschätzung allerdings n​icht für d​ie Fehler d​er Iterierten, sondern für d​as Residuum. Es gilt:

${\displaystyle \|r_{k}\|\leq 2\left({\frac {{\sqrt {\kappa (A)}}-1}{{\sqrt {\kappa (A)}}+1}}\right)^{k}\|r_{0}\|}$.

Dabei ist ${\displaystyle \kappa (A)}$ die Konditionszahl der Matrix ${\displaystyle A}$.

Beispiel-Implementierung in GNU Octave / Matlab

function [x,r] = minres(A,b,x0,maxit,tol)
  x = x0;
  r = b - A*x0;
  p0 = r;
  s0 = A*p0;
  p1 = p0;
  s1 = s0;
  for iter=[1:maxit]
    p2 = p1;p1 = p0;
    s2 = s1;s1 = s0;
    alpha = r'*s1/(s1'*s1);
    x += alpha*p1;
    r -= alpha*s1;
    if (r'*r < tol^2)
      break
    end
    p0 = s1;
    s0 = A*s1;
    beta1 = s0'*s1/(s1'*s1);
    p0 -= beta1*p1;
    s0 -= beta1*s1;
    if iter > 1
      beta2 = s0'*s2/(s2'*s2);
      p0 -= beta2*p2;
      s0 -= beta2*s2;
    end
  end
end

Einzelnachweise

1. Christopher C. Paige, Michael A. Saunders: Solution of sparse indefinite systems of linear equations. In: SIAM Journal on Numerical Analysis. Band 12, Nr. 4, 1975.
2. Sven Gross, Arnold Reusken: Numerical Methods for Two-phase Incompressible Flows. Springer, ISBN 978-3-642-19685-0, Kap. 5.2.