Achsensymmetrie

Achsensymmetrie ist die spiegelbildliche Anordnung von Zeichen zu beiden Seiten einer gedachten Linie.[1] In der Geometrie sind axiale Symmetrie oder Axialsymmetrie gleichbedeutende Bezeichnungen dieser Eigenschaft. Eine Figur heißt achsensymmetrisch, wenn sie durch die senkrechte Achsenspiegelung an ihrer Symmetrieachse auf sich selbst abgebildet wird.

Figuren mit ihren Symmetrieachsen (gestrichelt). Die Figur unten rechts ist nicht achsensymmetrisch.

Achsensymmetrie in der Architektur
(Herrensitz Castle Howard)

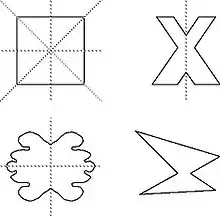
Im Falle einer zweidimensionalen Figur ist Achsensymmetrie gleichbedeutend mit Spiegelsymmetrie. In dreidimensionalen Räumen entspricht die Achsensymmetrie hingegen einer Drehsymmetrie um 180° (während die Spiegelsymmetrie im Dreidimensionalen eine Symmetrie zu einer Symmetrieebene ist).

Definition

Eine Figur ist achsensymmetrisch, falls es eine Gerade g gibt, so dass es zu jedem Punkt P der Figur einen weiteren (eventuell mit P identischen) Punkt P' der Figur gibt, so dass die Verbindungsstrecke [PP'] von dieser Geraden rechtwinklig halbiert wird.

Eine ebene Figur F heißt achsen- oder axialsymmetrisch, wenn sich in ihrer Ebene eine Gerade g angeben lässt, so dass F durch Spiegelung an g in sich selbst übergeführt wird.[2]

Die Gerade g wird dann Symmetrieachse genannt.

Beispiele

Wie man in der nebenstehenden Abbildung erkennen kann, hat das Quadrat genau vier Symmetrieachsen. Vierecke, die keine Quadrate sind, haben weniger oder gar keine Symmetrieachsen. Ein Rechteck hat zum Beispiel immer noch zwei Symmetrieachsen, und zwar die beiden Mittelsenkrechten der gegenüberliegenden Seiten und das gleichschenklige Trapez, das Drachenviereck und das Antiparallelogramm besitzen noch mindestens eine Symmetrieachse.
Der Kreis hat sogar unendlich viele Symmetrieachsen, da dieser bezüglich jedes Durchmessers symmetrisch ist.
Eine andere Figur mit unendlich vielen Symmetrieachsen ist die Gerade. Sie ist unendlich lang und damit symmetrisch bezüglich jeder zu ihr senkrechten Achse, sowie der auf ihr selbst liegenden Achse.
Nicht nur 2-dimensionale Figuren können achsensymmetrisch sein. So ist die Kugel bezüglich jeder Gerade durch den Mittelpunkt achsensymmetrisch. Dies darf man nicht mit der Ebenensymmetrie verwechseln. Die Kugel ist auch ebenensymmetrisch. Das heißt, sie ist symmetrisch bezüglich einer Spiegelung an einer Ebene, die den Mittelpunkt der Kugel enthält.
Auch der Quader ist achsensymmetrisch.
Der Graph der Kosinus-Funktion ist ebenfalls achsensymmetrisch zur y-Achse. Das Thema achsensymmetrischer Funktionen wird im folgenden Abschnitt genauer betrachtet.

Achsensymmetrie von Funktionsgraphen

Überblick

Funktion, deren Graph achsensymmetrisch zur Gerade x=a ist

Eine vor allem in der Schule beliebte Aufgabe besteht darin, für den Graphen einer Funktion $f\colon D\to \mathbb {R}$ die Achsensymmetrie nachzuweisen. Ist die y-Achse des Koordinatensystems die Symmetrieachse, so muss gezeigt werden, dass die Gleichung

f(-x)\,=\,f(x)

für alle x des Definitionsbereichs $D$ erfüllt ist. Dann sagt man, dass der Graph der Funktion $f$ symmetrisch bezüglich der y-Achse ist. Solche Funktionen nennt man auch gerade Funktionen. Diese Bedingung besagt, dass die Funktionswerte der Argumente $x$ und $-x$ übereinstimmen müssen.

Möchte man allgemeiner die Achsensymmetrie eines Funktionsgraphen bezüglich einer beliebigen zur y-Achse parallelen Geraden mit der Gleichung $x=a$ untersuchen, so muss man testen, ob die Funktion $f$ die Gleichung

f(a-x)\,=\,f(a+x)

für ein festes $a\in \mathbb {R}$ und für alle $x$ aus dem Definitionsbereich erfüllt. Durch Substitution von $x$ mit $x-a$ erhält man die äquivalente Bedingung

f(2a-x)\,=\,f(x).

Beispiele

Als Beispiel dient die quadratische Funktion

f(x)\,=\,x^{2}-1.

Anwendung der genannten Bedingung für die Achsensymmetrie in Bezug auf die y-Achse ergibt

f(-x)\,=\,(-x)^{2}-1=x^{2}-1=f(x).

Der Graph (eine Parabel) ist also symmetrisch bezüglich der y-Achse.

Nun wird ein Beispiel einer Funktion angeführt, deren Graph nicht symmetrisch bezüglich der y-Achse, aber doch achsensymmetrisch ist. Die Funktion

f(x)=x^{2}-4x+3

ist ein solches Beispiel. Die Behauptung ist, dass der Graph von $f$ achsensymmetrisch in Bezug auf die Senkrechte $x=2$ ist. Es gilt also $a=2$ und daraus folgt

{\begin{aligned}f(2a-x)&=f(4-x)\\&=(4-x)^{2}-4(4-x)+3\\&=(16-8x+x^{2})-(16-4x)+3\\&=16-8x+x^{2}-16+4x+3\\&=x^{2}-4x+3\\&=f(x)\end{aligned}}

Damit ist die Vermutung der Achsensymmetrie bestätigt.

Allgemein ist der Graph einer quadratischen Funktion $f(x)=ax^{2}+bx+c$ achsensymmetrisch bezüglich der vertikalen Geraden durch den Scheitelpunkt $S=(x_{s},y_{s})$ . Das sieht man leicht, wenn man den Funktionsterm in Scheitelpunktform $f(x)=a(x-x_{s})^{2}+y_{s}$ umschreibt.

Rotationskörper

Eine Klasse achsensymmetrischer Körper im 3-dimensionalen Raum sind die Rotationskörper. Ein dreidimensionales Objekt ist ein Rotationskörper, wenn eine Drehung um jeden beliebigen Winkel um eine fixierte Achse das Objekt auf sich selbst abbildet. Diese Achse ist die Symmetrieachse. Das einfachste Beispiel eines Rotationskörpers ist der Zylinder.

Ebenensymmetrie

Eine andere Verallgemeinerung der Achsensymmetrie auf den 3-dimensionalen Raum ist die Ebenensymmetrie. Eine Figur ist ebenensymmetrisch, falls es eine Ebene gibt, so dass unter Spiegelung an dieser die Figur auf sich selbst abgebildet wird.

Literatur

Achsensymmetrie. In: Duden online. Abgerufen am 21. November 2019.
Arnfried Kemnitz: Mathematik zum Studienbeginn. Grundlagenwissen für alle technischen, mathematisch-naturwissenschaftlichen und wirtschaftswissenschaftlichen Studiengänge. 9. überarbeitete und erweiterte Auflage. Springer-Verlag, Wiesbaden 2010, ISBN 978-3-8348-1293-3, S. 144 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 21. November 2019]).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Achsensymmetrie. In: Duden online. Abgerufen am 21. November 2019.

[2] Arnfried Kemnitz: Mathematik zum Studienbeginn. Grundlagenwissen für alle technischen, mathematisch-naturwissenschaftlichen und wirtschaftswissenschaftlichen Studiengänge. 9. überarbeitete und erweiterte Auflage. Springer-Verlag, Wiesbaden 2010, ISBN 978-3-8348-1293-3, S. 144 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 21. November 2019]).