Konvektive Koordinaten

Konvektive Koordinaten sind krummlinige Koordinaten, die an einen Träger gebunden sind und von allen Transformationen, die der Träger erfährt, mitgeführt werden, daher die Bezeichnung konvektiv. In der Kontinuumsmechanik ergeben sich konvektive Koordinaten auf natürliche Weise, wenn die Koordinatenlinien körperfeste Linien sind, die allen Bewegungen und Deformationen des Körpers folgen. Bildlich kann man sich ein Koordinatennetz auf eine Gummihaut aufgemalt denken, die dann gedehnt wird und das Koordinatennetz mitnimmt, siehe Abbildung rechts.

Auf einen Körper aufgetragene Koordinatenlinien folgen den Deformationen des Körpers

Praktische Bedeutung haben konvektive Koordinatensysteme in der Kinematik schlanker Strukturen (Stäbe, Balken) und dünnwandiger Strukturen (Schalen und Membranen), wo die Spannungen und Dehnungen parallel zu den Vorzugsrichtungen der Struktur interessieren. Außerdem können materielle Vorzugsrichtungen nicht isotroper Materialien, wie z. B. von Holz, oder Advektions-Diffusions-Probleme (z. B. Schadstoffausbreitung in der Atmosphäre oder im Grundwasser) in konvektiven Koordinaten beschrieben werden. In der Kinematik deformierbarer Körper bekommen die in der Kontinuumsmechanik benutzten Tensoren in konvektiven Koordinaten ausgedrückt besonders einfache Darstellungen.

Definition

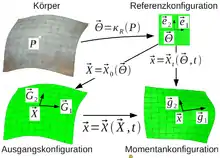
Konfigurationen und konvektive Koordinaten

Betrachtet wird ein deformierbarer Körper wie im Bild, der mittels Konfigurationen in einen euklidischen Vektorraum $\mathbb {V} ^{3}$ abgebildet wird. Die konvektiven Koordinaten eines materiellen Punktes $P$ werden durch die Referenzkonfiguration $\kappa _{R}(P)$ zugewiesen. Für jedes Partikel $P$ eines Körpers $K$ sind seine konvektiven Koordinaten gegeben durch:

{\begin{array}{llll}\kappa _{R}:&K&\rightarrow &V_{R}\subset \mathbb {V} ^{3}\\&P&\mapsto &{\vec {\Theta }}=(\Theta _{1},\Theta _{2},\Theta _{3})\end{array}}

Diese Zuordnung ist vom gewählten Bezugssystem des Beobachters, von der Zeit und vom physikalischen Raum unserer Anschauung unabhängig. Für den viereckigen Körper im Bild eignet sich z. B. das Einheitsquadrat $V_{R}=[0,1]^{2}$ als Bildbereich. $\kappa _{R}$ ist ein-eindeutig (bijektiv), so dass ${\vec {\Theta }}$ auch der Benennung des Partikels $P$ dienen kann. Weil die Koordinaten ${\vec {\Theta }}$ an das Partikel gebunden sind, werden sie von jeder Bewegung des Partikels mitgenommen.

Tangenten- und Gradientenvektoren

Koordinatenlinie von

\Theta _{1}

mit Tangentenvektor

{\vec {G}}_{1}

und Gradientenvektor

{\vec {G}}^{1}

im Punkt

{\vec {X}}

Die kovarianten Tangentenvektoren

{\vec {G}}_{1,2,3}

und

{\vec {g}}_{1,2,3}

an materielle Koordinatenlinien (schwarz) in der Ausgangs- bzw. Momentankonfiguration spannen Tangentialräume (gelb) auf. Die kontravarianten Basisvektoren

\color {blue}{\vec {G}}^{1,2,3}

und

\color {blue}{\vec {g}}^{1,2,3}

spannen Kotangentialräume auf (nicht dargestellt)

Die Bewegungsfunktion ${\vec {x}}={\vec {\chi }}_{t}({\vec {\Theta }},t)\in \mathbb {V} ^{3}$ beschreibt die Bewegung des Partikels ${\vec {\Theta }}$ durch den Raum unserer Anschauung und liefert uns ein Objekt unserer Anschauung, weil diese Positionen vom Körper einmal eingenommen wurden. Die Bewegung startet zu einem bestimmten Zeitpunkt $t_{0}$ , in dem sich der Körper in der Ausgangskonfiguration befindet. Die Funktion

{\vec {\chi }}_{0}({\vec {\Theta }}):={\vec {\chi }}_{t}({\vec {\Theta }},t_{0})={\vec {X}}=\sum _{i=1}^{3}X_{i}{\vec {e}}_{i}

ordnet den Koordinaten ${\vec {\Theta }}$ ein-eindeutig (bijektiv) einen Punkt ${\vec {X}}$ im Raum zu, den das Partikel zum Zeitpunkt $t_{0}$ eingenommen hat. Der Vektor ${\vec {X}}$ hat materielle Koordinaten $X_{1,2,3}$ bezüglich der Standardbasis ${\vec {e}}_{1,2,3}$ . Wegen der Bijektivität kann

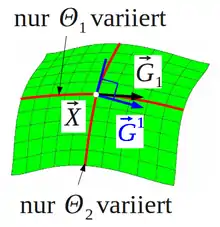
{\vec {X}}=:{\vec {\chi }}_{0}({\vec {\Theta }})\quad \Leftrightarrow \quad {\vec {\Theta }}=:{\vec {\chi }}_{0}^{-1}({\vec {X}})

geschrieben werden. Variiert im Vektor ${\vec {\Theta }}$ nur eine Koordinate $\Theta _{i}$ , dann fährt ${\vec {\chi }}_{0}({\vec {\Theta }})$ eine materielle Koordinatenlinie ab, die im allgemeinen Fall eine Kurve im Raum ist, siehe obere Abbildung rechts. Die Tangentenvektoren

{\vec {G}}_{i}={\frac {\mathrm {d} {\vec {\chi }}_{0}}{\mathrm {d} \Theta _{i}}}=\sum _{j=1}^{3}{\frac {\mathrm {d} \chi _{0j}}{\mathrm {d} \Theta _{i}}}{\vec {e}}_{j}

an diese Kurven werden kovariante Basisvektoren des krummlinigen Koordinatensystems genannt. Die Richtung, in der sich die Koordinate $\Theta _{i}$ am stärksten ändert, sind die Gradienten

{\vec {G}}^{i}={\frac {\mathrm {d} \Theta _{i}}{\mathrm {d} {\vec {X}}}}:=\mathrm {GRAD} (\Theta _{i})=\sum _{j=1}^{3}{\frac {\mathrm {d} \Theta _{i}}{\mathrm {d} X_{j}}}{\vec {e}}_{j}

die die kontravarianten Basisvektoren ${\vec {G}}^{i}$ in einem materiellen Punkt darstellen. Wegen

{\begin{aligned}{\frac {\mathrm {d} \Theta _{i}}{\mathrm {d} \Theta _{j}}}=&\sum _{k=1}^{3}{\frac {\mathrm {d} \Theta _{i}}{\mathrm {d} X_{k}}}\cdot {\frac {\mathrm {d} X_{k}}{\mathrm {d} \Theta _{j}}}=\sum _{k,l=1}^{3}{\frac {\mathrm {d} \Theta _{i}}{\mathrm {d} X_{k}}}{\vec {e}}_{k}\cdot {\frac {\mathrm {d} X_{l}}{\mathrm {d} \Theta _{j}}}{\vec {e}}_{l}\\=&{\vec {G}}^{i}\cdot {\vec {G}}_{j}=\left\{{\begin{array}{lll}1&\mathrm {falls} &i=j\\0&\mathrm {sonst} &\end{array}}\right.\end{aligned}}

sind die ko- und kontravarianten Basisvektoren dual zueinander und die kontravarianten Basisvektoren können aus

{\begin{aligned}\mathbf {J} =&\sum _{i,j=1}^{3}{\frac {\mathrm {d} \chi _{0i}}{\mathrm {d} \Theta _{j}}}{\vec {e}}_{i}\otimes {\vec {e}}_{j}=\sum _{j=1}^{3}{\vec {G}}_{j}\otimes {\vec {e}}_{j}\\\rightarrow \mathbf {J} ^{-1}=&\displaystyle \left(\sum _{j=1}^{3}{\vec {G}}_{j}\otimes {\vec {e}}_{j}\right)^{-1}=\sum _{i=1}^{3}{\vec {e}}_{i}\otimes {\vec {G}}^{i}\end{aligned}}

berechnet werden. Darin wurde das dyadische Produkt " $\otimes$ " benutzt.

Der zwischen der Referenzkonfiguration und der Ausgangskonfiguration arbeitende Deformationsgradient J enthält die kovarianten Basisvektoren ${\vec {G}}_{i}$ in den Spalten und die kontravarianten Basisvektoren ${\vec {G}}^{i}$ finden sich in den Zeilen seiner Inversen $\mathbf {J} ^{-1}$ .

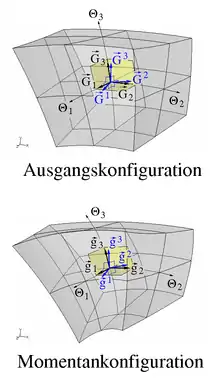
Die ko- und kontravarianten Basisvektoren werden nur lokal (in den Tangentialräumen) im Punkt ${\vec {X}}$ als Basissystem für Vektor- und Tensorfelder, nicht aber für Ortsvektoren, benutzt: Die kovarianten Basisvektoren ${\vec {G}}_{i}$ bilden eine Basis des Tangentialraumes $T_{\vec {X}}\mathbb {V} ^{3}$ und die kontravarianten Basisvektoren ${\vec {G}}^{i}$ bilden eine Basis des Kotangentialraumes $T_{\vec {X}}^{\ast }\mathbb {V} ^{3}$ im Punkt ${\vec {X}}$ , siehe untere Abbildung rechts.

Im Zuge der Bewegung entsteht in jedem Punkt und zu jedem Zeitpunkt $t>t_{0}$ einen Satz kovarianter Basisvektoren ${\vec {g}}_{i}$ und kontravarianter Basisvektoren ${\vec {g}}^{i}$ , die die Tangenten bzw. Gradienten der materiellen Koordinatenlinien im deformierten Körper zur Zeit $t$ sind. Sie sind mithin Basen der Tangentialräume $T_{\vec {x}}\mathbb {V} ^{3}$ bzw. $T_{\vec {x}}^{\ast }\mathbb {V} ^{3}$ .

Differentialoperatoren und Nabla-Operator

Die Differentialoperatoren Gradient (grad), Divergenz (div) und Rotation (rot) aus der Vektoranalysis können mit dem Nabla-Operator $\nabla$ definiert werden. In konvektiven Koordinaten hat der Nabla-Operator in der Lagrange’schen Darstellung die Form:

\nabla _{0}:=\sum _{i=1}^{3}{\vec {G}}^{i}{\frac {\partial }{\partial \Theta _{i}}}

Die Gradienten von Skalar- und Vektorfeldern werden mit ihm wie folgt dargestellt[1]:

Skalarfeld	$\mathrm {GRAD} (\phi ):=\nabla _{0}\,\phi =\sum _{i=1}^{3}{\frac {\partial \phi }{\partial \Theta _{i}}}{\vec {G}}^{i}=:{\frac {\partial \phi }{\partial {\vec {X}}}}$
Vektorfeld	$\mathrm {GRAD} ({\vec {v}}):=(\nabla _{0}\otimes {\vec {v}})^{\top }=\sum _{i=1}^{3}{\frac {\partial {\vec {v}}}{\partial {\Theta }_{i}}}\otimes {\vec {G}}^{i}=:{\frac {\partial {\vec {v}}}{\partial {\vec {X}}}}$

Die Divergenzen werden aus dem Skalarprodukt mit $\nabla _{0}$ erhalten[1]:

Vektorfeld	$\mathrm {DIV} ({\vec {v}}):=\nabla _{0}\cdot {\vec {v}}=\sum _{i=1}^{3}{\frac {\partial {\vec {v}}}{\partial \Theta _{i}}}\cdot {\vec {G}}^{i}=\mathrm {Sp} \left({\frac {\partial {\vec {v}}}{\partial {\vec {X}}}}\right)$
Tensorfeld	$\mathrm {DIV} (\mathbf {T} ):=\nabla _{0}\cdot \mathbf {T} =\sum _{i=1}^{3}{\vec {G}}^{i}\cdot {\frac {\partial \mathbf {T} }{\partial \Theta _{i}}}$

Der Operator Sp bildet die Spur. Die Rotation eines Vektorfeldes entsteht mit dem Kreuzprodukt:

\mathrm {ROT} ({\vec {v}}):=\nabla _{0}\times {\vec {v}}=\sum _{i=1}^{3}{\vec {G}}^{i}\times {\frac {\partial {\vec {v}}}{\partial \Theta }}_{i}

Entsprechende Operatoren $\mathrm {div}$ , $\mathrm {grad}$ und $\mathrm {rot}$ für Felder in der Euler’schen Darstellung liefert der Nabla-Operator

\nabla _{t}:=\sum _{i=1}^{3}{\vec {g}}^{i}{\frac {\partial }{\partial \Theta _{i}}}

Der Einheitstensor

Der Einheitstensor $\mathbf {1}$ bildet jeden Vektor auf sich selbst ab. Bezüglich der ko- und kontravarianten Basisvektoren lauten seine Darstellungen:

\mathbf {1} =\sum _{i=1}^{3}{\vec {G}}^{i}\otimes {\vec {G}}_{i}=\sum _{i=1}^{3}{\vec {G}}_{i}\otimes {\vec {G}}^{i}=\sum _{i,j=1}^{3}G_{ij}{\vec {G}}^{i}\otimes {\vec {G}}^{j}=\sum _{i,j=1}^{3}G^{ij}{\vec {G}}_{i}\otimes {\vec {G}}_{j}

Die Skalarprodukte der kovarianten Basisvektoren

G_{ij}={\vec {G}}_{i}\cdot {\vec {G}}_{j}

heißen kovariante Metrikkoeffizienten (des Tangentialraumes $T_{\vec {X}}\mathbb {V} ^{3}$ ). Entsprechend sind die Skalarprodukte der kontravarianten Basisvektoren

G^{ij}={\vec {G}}^{i}\cdot {\vec {G}}^{j}

kontravariante Metrikkoeffizienten (des Kotangentialraumes $T_{\vec {X}}^{\ast }\mathbb {V} ^{3}$ ).

In der Euler’schen Betrachtungsweise ist entsprechend

\mathbf {1} =\sum _{i=1}^{3}{\vec {g}}^{i}\otimes {\vec {g}}_{i}=\sum _{i=1}^{3}{\vec {g}}_{i}\otimes {\vec {g}}^{i}=\sum _{i,j=1}^{3}g_{ij}{\vec {g}}^{i}\otimes {\vec {g}}^{j}=\sum _{i,j=1}^{3}g^{ij}{\vec {g}}_{i}\otimes {\vec {g}}_{j}

mit den ko- und kontravarianten Metrikkoeffizienten $g_{ij}={\vec {g}}_{i}\cdot {\vec {g}}_{j}$ bzw. $g^{ij}={\vec {g}}^{i}\cdot {\vec {g}}^{j}$ (des Tangentialraumes $T_{\vec {x}}\mathbb {V} ^{3}$ bzw. Kotangentialraumes $T_{\vec {x}}^{\ast }\mathbb {V} ^{3}$ ).

Deformationsgradient

In konvektiven Koordinaten ausgedrückt bekommt der Deformationsgradient $\mathbf {F}$ eine besonders einfache Form. Der Deformationsgradient bildet gemäß seiner Definition die Tangentenvektoren an materielle Linien in der Ausgangskonfiguration auf die in der Momentankonfiguration ab und diese Tangentenvektoren sind gerade die kovarianten Basisvektoren ${\vec {G}}_{i}$ bzw. ${\vec {g}}_{i}$ . Also ist

{\vec {g}}_{i}=\mathbf {F} \cdot {\vec {G}}_{i}\quad \Leftrightarrow \quad \mathbf {F} =\sum _{i=1}^{3}{\vec {g}}_{i}\otimes {\vec {G}}^{i}

Das ergibt sich auch aus der Ableitung der Bewegungsfunktion ${\vec {x}}={\vec {\chi }}({\vec {X}},t)={\vec {\chi }}_{t}({\vec {\Theta }},t)$ :

\mathbf {F} =\mathrm {GRAD} \;{\vec {\chi }}({\vec {X}},t)={\vec {\chi }}_{t}\otimes \nabla _{0}=\sum _{i=1}^{3}{\frac {\mathrm {d} {\vec {\chi }}_{t}}{\mathrm {d} \Theta _{i}}}\otimes {\vec {G}}^{i}=\sum _{i=1}^{3}{\vec {g}}_{i}\otimes {\vec {G}}^{i}

In dieser Darstellung lässt sich auch sofort mit

\mathbf {F} ^{-1}=\sum _{i=1}^{3}{\vec {G}}_{i}\otimes {\vec {g}}^{i}

die Inverse des Deformationsgradienten angeben. Der transponiert inverse Deformationensgradient bildet die kontravarianten Basisvektoren aufeinander ab:

\mathbf {F} ^{\top -1}=\sum _{i=1}^{3}{\vec {g}}^{i}\otimes {\vec {G}}_{i}\quad \Leftrightarrow \quad {\vec {g}}^{i}=\mathbf {F} ^{\top -1}\cdot {\vec {G}}^{i}

Räumlicher Geschwindigkeitsgradient

Die materielle Zeitableitung des Deformationsgradienten ist der materielle Geschwindigkeitsgradient

{\dot {\mathbf {F} }}=\sum _{i=1}^{3}{\dot {\vec {g}}}_{i}\otimes {\vec {G}}^{i}

denn die Ausgangskonfiguration hängt nicht von der Zeit ab und das gilt dann auch für die Basisvektoren ${\vec {G}}_{i}$ und ${\vec {G}}^{i}$ . Der räumliche Geschwindigkeitsgradient $\mathbf {l}$ bekommt in konvektiven Koordinaten die einfache Form

\mathbf {l} =\mathrm {grad} ({\vec {v}}({\vec {x}},t))={\dot {\mathbf {F} }}\cdot \mathbf {F} ^{-1}=\sum _{i=1}^{3}{\dot {\vec {g}}}_{i}\otimes {\vec {g}}^{i}=-\sum _{i=1}^{3}{\vec {g}}_{i}\otimes {\dot {\vec {g}}}^{i}

worin ${\vec {v}}({\vec {x}},t)$ die Geschwindigkeit eines Partikels am Ort ${\vec {x}}$ zur Zeit $t$ ist. Der räumliche Geschwindigkeitsgradient transformiert die Basisvektoren in ihre Raten:

{\dot {\vec {g}}}_{i}=\mathbf {l} \cdot {\vec {g}}_{i}

und

{\dot {\vec {g}}}^{i}=-\mathbf {l} ^{\top }\cdot {\vec {g}}^{i}

Streck-, Verzerrungs- und Spannungstensoren

Die folgenden Tensoren treten in der Kontinuumsmechanik auf. Ihre Darstellung in konvektiven Koordinaten ist in der Tabelle zusammengestellt.

Name	Darstellung in konvektiven Koordinaten
Deformationsgradient	$\mathbf {F} =\sum _{i=1}^{3}{\vec {g}}_{i}\otimes {\vec {G}}^{i}$
Rechter Cauchy-Green Tensor	$\mathbf {C} =\mathbf {F} ^{\top }\cdot \mathbf {F} =\sum _{i,j=1}^{3}g_{ij}{\vec {G}}^{i}\otimes {\vec {G}}^{j}$
Linker Cauchy-Green Tensor	$\mathbf {b} =\mathbf {F\cdot F} ^{\top }=\sum _{i,j=1}^{3}G^{ij}{\vec {g}}_{i}\otimes {\vec {g}}_{j}$
Green-Lagrange-Verzerrungstensor	$\mathbf {E} ={\frac {1}{2}}(\mathbf {F} ^{\top }\cdot \mathbf {F} -\mathbf {1} )=\sum _{i,j=1}^{3}E_{ij}{\vec {G}}^{i}\otimes {\vec {G}}^{j}$ mit $E_{ij}={\frac {1}{2}}(g_{ij}-G_{ij})$
Euler-Almansi-Verzerrungstensor	$\mathbf {e} ={\frac {1}{2}}(\mathbf {1} -\mathbf {F} ^{\top -1}\cdot \mathbf {F} ^{-1})=\sum _{i,j=1}^{3}E_{ij}{\vec {g}}^{i}\otimes {\vec {g}}^{j}$
Räumlicher Geschwindigkeitsgradient	$\mathbf {l} =\sum _{i=1}^{3}{\dot {\vec {g}}}_{i}\otimes {\vec {g}}^{i}=-\sum _{i=1}^{3}{\vec {g}}_{i}\otimes {\dot {\vec {g}}}^{i}$
Räumlicher Verzerrungsgeschwindigkeitstensor	$\mathbf {d} ={\frac {1}{2}}\sum _{i,j=1}^{3}{\dot {g}}_{ij}{\vec {g}}^{i}\otimes {\vec {g}}^{j}=-{\frac {1}{2}}\sum _{i,j=1}^{3}{\dot {g}}^{ij}{\vec {g}}_{i}\otimes {\vec {g}}_{j}$
Cauchy’scher Spannungstensor	${\boldsymbol {\sigma }}=\sum _{i,j=1}^{3}\sigma ^{ij}{\vec {g}}_{i}\otimes {\vec {g}}_{j}$
Gewichteter Cauchy’scher Spannungstensor	$\mathbf {S} =\mathrm {det} (\mathbf {F} ){\boldsymbol {\sigma }}=\sum _{i,j=1}^{3}{\tilde {T}}^{ij}{\vec {g}}_{i}\otimes {\vec {g}}_{j}$
Nennspannungstensor	$\mathbf {N} =\mathrm {det} (\mathbf {F} )\mathbf {F} ^{-1}\cdot {\boldsymbol {\sigma }}=\sum _{i,j=1}^{3}{\tilde {T}}^{ij}{\vec {G}}_{i}\otimes {\vec {g}}_{j}$
Erster Piola-Kirchoff’scher Spannungstensor	$\mathbf {P} =\mathbf {N} ^{\top }=\mathrm {det} (\mathbf {F} ){\boldsymbol {\sigma }}\cdot \mathbf {F} ^{\top -1}=\sum _{i,j=1}^{3}{\tilde {T}}^{ij}{\vec {g}}_{i}\otimes {\vec {G}}_{j}$
Zweiter Piola-Kirchoff’scher Spannungstensor	${\tilde {\mathbf {T} }}=\mathrm {det} (\mathbf {F} )\mathbf {F} ^{-1}\cdot {\boldsymbol {\sigma }}\cdot \mathbf {F} ^{\top -1}=\sum _{i,j=1}^{3}{\tilde {T}}^{ij}{\vec {G}}_{i}\otimes {\vec {G}}_{j}$

Weil der rechte Cauchy-Green Tensor $\mathbf {C}$ , der Green-Lagrange-Verzerrungstensor $\mathbf {E}$ und der Euler-Almansi-Tensor $\mathbf {e}$ in ihrer (hier angegebenen) natürlichen Form mit den kovarianten Komponenten $g_{ij}$ bzw. $E_{ij}$ gebildet werden, werden diese Tensoren üblicherweise als kovariante Tensoren bezeichnet. Die Spannungstensoren ${\boldsymbol {\sigma }},\mathbf {S}$ und $\mathbf {\tilde {T}}$ sind entsprechend kontravariante Tensoren.

Objektive Zeitableitungen

Objektive Größen sind solche, die von bewegten Beobachtern in gleicher Weise wahrgenommen werden. Die Zeitableitung von Tensoren ist im Allgemeinen nicht objektiv. Die konvektiven ko- bzw. kontravarianten Oldroyd-Ableitungen objektiver Tensoren sind jedoch objektiv und schreiben sich in konvektiven Koordinaten besonders einfach.

Die Kovariante Oldroyd-Ableitung, z. B. von $\mathbf {e} =\sum _{i,j=1}^{3}E_{ij}{\vec {g}}^{i}\otimes {\vec {g}}^{j}$ lautet

{\stackrel {\Delta }{\mathbf {e} }}:={\dot {\mathbf {e} }}+\mathbf {e\cdot l} +\mathbf {l^{\top }\cdot e} =\sum _{i,j=1}^{3}{\dot {E}}_{ij}{\vec {g}}^{i}\otimes {\vec {g}}^{j}

Die Kontravariante Oldroyd-Ableitung, z. B. von $\mathbf {S} =\sum _{i,j=1}^{3}{\tilde {T}}^{ij}{\vec {g}}_{i}\otimes {\vec {g}}_{j}$ , ergibt sich ähnlich:

{\stackrel {\nabla }{\mathbf {S} }}:={\dot {\mathbf {S} }}-\mathbf {l\cdot S} -\mathbf {S\cdot l} ^{\top }=\sum _{i,j=1}^{3}{\dot {\tilde {T}}}^{ij}{\vec {g}}_{i}\otimes {\vec {g}}_{j}

Daraus leiten sich auch die Bezeichnungen konvektiv kovariant bzw. konvektiv kontravariant der Oldroyd-Ableitungen ab. Bemerkenswert sind die übereinstimmenden Transformationseigenschaften der kovarianten Tensoren

\mathbf {e} =\mathbf {F} ^{\top -1}\cdot \mathbf {E\cdot F} ^{-1}

und

{\stackrel {\Delta }{\mathbf {e} }}=\mathbf {F} ^{\top -1}\cdot {\dot {\mathbf {E} }}\cdot \mathbf {F} ^{-1}

sowie der kontravarianten Tensoren

\mathbf {S} =\mathbf {F} \cdot {\tilde {\mathbf {T} }}\cdot \mathbf {F} ^{\top }

und

{\stackrel {\nabla }{\mathbf {S} }}=\mathbf {F} \cdot {\dot {\tilde {\mathbf {T} }}}\cdot \mathbf {F} ^{\top }

Siehe auch den Abschnitt Objektive Zeitableitungen im Artikel zum Geschwindigkeitsgradient.

Beispiel

Parallelogramm in Ausgangs- und Momentankonfiguration

Ein Parallelogramm mit Grundseite und Höhe $L$ und Neigungswinkel $\alpha$ wird zu einem flächengleichen Quadrat verformt, siehe Bild. Als Referenzkonfiguration eignet sich das Einheitsquadrat

\Theta _{1},\Theta _{2}\in [0,L]^{2}\subset \mathbb {R} ^{2}

In der Ausgangskonfiguration haben die Punkte des Parallelogramms die Koordinaten:

{\vec {X}}={\vec {\chi }}_{0}(\Theta _{1},\Theta _{2})=\left({\begin{array}{c}\Theta _{1}+\tan(\alpha )\Theta _{2}\\\Theta _{2}\end{array}}\right)

Die kovarianten Basisvektoren sind

{\vec {G}}_{1}={\frac {\mathrm {d} {\vec {X}}}{\mathrm {d} \Theta _{1}}}=\left({\begin{array}{c}1\\0\end{array}}\right)={\vec {e}}_{x}\,,\;{\vec {G}}_{2}={\frac {\mathrm {d} {\vec {X}}}{\mathrm {d} \Theta _{2}}}=\left({\begin{array}{c}\tan(\alpha )\\1\end{array}}\right)

Sie stehen spaltenweise im Gradient $\mathbf {J}$ und die kontravarianten Basisvektoren entspringen den Zeilen der Inversen:

\mathbf {J} =\sum _{i,j=1}^{2}{\frac {\mathrm {d} X_{i}}{\mathrm {d} \Theta _{j}}}{\vec {e}}_{i}\otimes {\vec {e}}_{j}=\left({\begin{array}{cc}1&\tan(\alpha )\\0&1\end{array}}\right)\;\rightarrow \;\mathbf {J} ^{-1}=\left({\begin{array}{cc}1&-\tan(\alpha )\\0&1\end{array}}\right)

\rightarrow {\vec {G}}^{1}=\left({\begin{array}{c}1\\-\tan(\alpha )\end{array}}\right)\,,\;{\vec {G}}^{2}=\left({\begin{array}{c}0\\1\end{array}}\right)

In der Momentankonfiguration ist $\alpha =0^{\circ }$ :

{\vec {x}}={\vec {\chi }}_{t}(\Theta _{1},\Theta _{2})=\left({\begin{array}{c}\Theta _{1}\\\Theta _{2}\end{array}}\right)

und die konvektiven ko- und kontravarianten Basisvektoren bilden die Standardbasis

{\vec {g}}_{1}={\vec {g}}^{1}={\vec {e}}_{x}=\left({\begin{array}{c}1\\0\end{array}}\right)\,,\;{\vec {g}}_{2}={\vec {g}}^{2}={\vec {e}}_{y}=\left({\begin{array}{c}0\\1\end{array}}\right)

Der Deformationsgradient

{\begin{aligned}\mathbf {F} =&\sum _{i=1}^{2}{\vec {g}}_{i}\otimes {\vec {G}}^{i}=\left({\begin{array}{c}1\\0\end{array}}\right)\otimes \left({\begin{array}{c}1\\-\tan(\alpha )\end{array}}\right)+\left({\begin{array}{c}0\\1\end{array}}\right)\otimes \left({\begin{array}{c}0\\1\end{array}}\right)\\=&\left({\begin{array}{cc}1&-\tan(\alpha )\\0&1\end{array}}\right)\end{aligned}}

ist ortsunabhängig und hat die Determinante eins, was die Erhaltung des Flächeninhalts differentialgeometrisch nachweist. Die kovarianten Metrikkoeffizienten lauten

{\begin{array}{lll}G_{11}=1\,,&G_{12}=G_{21}=\tan(\alpha )\,,&G_{22}=1+\tan {(\alpha )}^{2}\\\;g_{11}=1\,,&\;g_{12}=\;g_{21}=0\,,&\;g_{22}=1\end{array}}

Damit kann der Green-Lagrange-Verzerrungstensor berechnet werden:

{\begin{aligned}\mathbf {E} =&\sum _{i,j=1}^{2}{\frac {1}{2}}(g_{ij}-G_{ij}){\vec {G}}^{i}\otimes {\vec {G}}^{j}={\frac {1}{2}}\left({\begin{array}{cc}0&-\tan(\alpha )\\-\tan(\alpha )&\tan(\alpha )^{2}\end{array}}\right)\\=&{\frac {1}{2}}(\mathbf {F} ^{\top }\cdot \mathbf {F} -\mathbf {1} )\end{aligned}}

Siehe auch

Fußnoten

In der Literatur kommen auch andere Definitionen vor, siehe den Hauptartikel zum Nabla-Operator.

Literatur

H. Parisch: Festkörper Kontinuumsmechanik. B. G. Teubner, 2003, ISBN 3-519-00434-8.
H. Bertram: Axiomatische Einführung in die Kontinuumsmechanik. Wissenschaftsverlag, 1989, ISBN 3-411-14031-3.
P. Haupt: Continuum Mechanics and Theory of Materials. Springer, 2010, ISBN 978-3-642-07718-0.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[version-1] In der Literatur kommen auch andere Definitionen vor, siehe den Hauptartikel zum Nabla-Operator.