Osmose

Als Osmose (altgriechisch ὠσμός ōsmós „Eindringen“, „Stoß“, „Schub“, „Antrieb“) wird in den Naturwissenschaften der gerichtete Fluss von Teilchen durch eine selektiv- oder semipermeable Trennschicht bezeichnet. Häufig wird Osmose als die spontane Passage von Wasser oder eines anderen Lösungsmittels durch eine semipermeable Membran beschrieben, die für das Lösungsmittel, jedoch nicht die darin gelösten Stoffe durchlässig ist.

Osmose ist in der Natur von zentraler Bedeutung, insbesondere für die Regulation des Wasserhaushalts von Lebewesen und ihren Zellen. Als Trennverfahren findet sie Anwendung in Medizin und Verfahrenstechnik und sie wird in Osmosekraftwerken zur Energiegewinnung eingesetzt. Während die Osmose im Rahmen der statistischen Mechanik[1] sowie der Nichtgleichgewichtsthermodynamik[2] theoretisch erklärt wird, sind die physikalischen Abläufe auf mikroskopisch-molekularer Ebene auch zu Beginn des 21. Jahrhunderts noch Gegenstand von Gelehrtenstreit und aktiver Forschungstätigkeit.[3][4][5]

Ein anschauliches Beispiel für die Wirkung der Osmose ist das Aufplatzen reifer Kirschen nach Benetzung mit Regenwasser. Das Wasser auf der Außenseite der Frucht enthält nur sehr wenig gelöste Teilchen, hat also ein hohes chemisches Potential. Es dringt durch die äußere Haut in die Frucht ein, in der das Wasser als Lösungsmittel durch den hohen Zuckergehalt und andere gelöste Stoffe ein niedriges chemisches Potential aufweist. Durch den Wassereinstrom steigt der Druck im Inneren der Frucht und führt zum Aufreißen ihrer äußeren Haut. Diese ist neben anderen Stoffen für Wasser durchlässig, nicht jedoch für Zuckermoleküle; aufgrund dieser Eigenschaften wirkt sie als semipermeable Membran. Wassermoleküle können diese Membran prinzipiell in beide Richtungen passieren, werden jedoch im Inneren der Frucht stärker „festgehalten“. Die Wassermoleküle müssen dort mit den anderen gelösten Molekülen und Teilchen um den Zugang zur Membran konkurrieren, so dass weniger Wassermoleküle pro Zeiteinheit nach außen dringen als umgekehrt.

Triebkraft der spontan ablaufenden Osmose ist der Unterschied zwischen den chemischen Potentialen eines oder mehrerer Stoffe in den durch eine Membran getrennten Phasen. Diese können aus flüssigen und gasförmigen Lösungen oder Reinstoffen bestehen. Teilchen (Atome, Moleküle oder Ionen) der Komponenten, für die die Membran durchlässig ist, diffundieren in Richtung ihres niedrigeren chemischen Potentials. Der aus dieser Bewegung resultierende Mischungsvorgang verringert die Gibbs-Energie (oder freie Enthalpie) des Gesamtsystems; daher läuft der Vorgang ohne Energiezufuhr ab (siehe auch exergone und endergone Reaktionen). Im Allgemeinen ist es ein Lösungsmittel, das aufgrund der unterschiedlichen Anzahl gelöster Teilchen in Richtung seines niedrigeren chemischen Potentials diffundiert.

In geschlossenen Systemen erfolgt durch Osmose ein Ausgleich der Potentialdifferenzen, die osmotische Bewegung hält solange an, bis das chemische Potential der diffundierenden Komponenten auf beiden Seiten der Membran ausgeglichen ist; zwischen beiden Phasen hat sich dann ein thermodynamisches Gleichgewicht eingestellt. Erfolgt der Stofffluss in ein geschlossenes Volumen, muss sich zwangsläufig der Druck in diesem Volumen (der Seite mit dem anfangs niedrigeren Potential) erhöhen; diese Differenz wird als osmotischer Druck bezeichnet. Der osmotische Druck ist eine kolligative Eigenschaft, da er von der Anzahl der gelösten Teilchen abhängt.

Geschichte und Definitionen des Begriffs Osmose

Geschichte

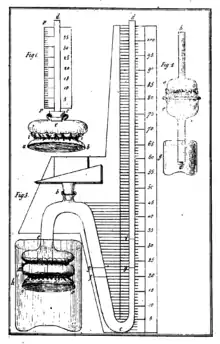
Dutrochets Endosmometer aus Nouvelles recherches

Im Jahre 1748 beschrieb Jean-Antoine Nollet, Professor für Experimentalphysik am Collège de Navarre in Paris, ein Experiment, bei dem ein Zylinder mit „Weingeist“ befüllt, mit einer entfetteten Schweinsblase verschlossen und aufrecht in Wasser getaucht wurde. Innerhalb weniger Stunden strömte so viel Wasser in den Zylinder, dass sich die Blase unter großem Druck nach außen wölbte; nach Anstechen mit einer Nadel schoss Flüssigkeit als kleine Fontäne in die Höhe.[6][7] Während die Schweinsblase für Wasser durchlässig ist, kann Alkohol durch diese nicht entweichen; Nollet hatte mit seinem Experiment die Existenz semipermeabler Membranen demonstriert.

„Osmose“ als Wortbestandteil verwendete erstmals der französische Botaniker Henri Dutrochet; er bezeichnete den Einstrom von Wasser in eine mit einer Schweinsblase umschlossene Messkammer als Endosmose, die Auswärtsbewegung als Exosmose. Dutrochet konstruierte mit dem Endosmometer als erster eine Vorrichtung zum Nachweis des osmotischen Drucks und postulierte die zentrale Bedeutung der Osmose für alle Lebensprozesse.[8][9] „Osmotisch“ (engl. osmotic) als Adjektiv wurde 1854 von dem schottischen Chemiker Thomas Graham geprägt.[7]

1864 gelang dem Chemiker und Privatgelehrten Moritz Traube die Herstellung von künstlichen semipermeablen Membranen, die für Zucker und eine Reihe anderer organischer Stoffe undurchlässig waren. 1877 beschrieb der deutsche Botaniker Wilhelm Pfeffer erstmals eine Methode zur quantitativen Messung des osmotischen Drucks wässriger Lösungen. Dazu entwickelte er die nach ihm benannte Pfeffersche Zelle, ein Osmometer aus porösem Ton, den er mit den von Traube entdeckten kolloidalen Niederschlagsmembranen wie Kupfer(II)-hexacyanoferrat(II) beschichtete.[10]

Das Pfeffersche Verfahren zur Messung des osmotischen Drucks wurde um die Jahrhundertwende durch Harmon Northrop Morse wesentlich verbessert, der das Membranmaterial mittels Elektrolyse auf die Wände der Tonzellen aufbrachte[11] und ermöglichte dadurch Messungen bis zum 270fachen des Atmosphärendrucks.[12]

Der niederländische Chemiker Jacobus Henricus van ’t Hoff veröffentlichte zehn Jahre nach Pfeffer seine wegweisende Arbeit zur Analogie von Gasdruck und osmotischem Druck von Lösungen,[13] für die er 1901, neben anderen Leistungen, mit dem ersten Nobelpreis für Chemie ausgezeichnet wurde.[14] 1905 veröffentlichte Albert Einstein seine grundlegende Arbeit zur Erklärung der Osmose mit Mitteln der „molekularkinetischen Theorie“.[15] 1958 definierten Ora Kedem und Aharon Katchalsky den Begriff des osmotischen Flusses im Rahmen der Onsagerschen Reziprozitätsbeziehungen und etablierten die Theorie der Membranen in Nichtgleichgewichtssystemen.[2]

Die Entwicklung geeigneter Membranen, zunächst aus Celluloseacetat Ende der 1950er Jahre,[16] etwas später dann synthetische asymmetrische Membranen[17] ermöglichte die Nutzung der Umkehrosmose zur Trinkwasseraufbereitung.[18] Der erste Prototyp eines Osmosekraftwerks wurde 2009 in Norwegen in Betrieb genommen.

Definitionen

In der Literatur wird der Begriff Osmose durchaus uneinheitlich, teils auch widersprüchlich definiert, zwei Beispiele:

„Unter Osmose versteht man die Diffusion von Teilchen durch eine selektiv permeable Membran, wie sie eine biologische Membran darstellt.“[19]
„Das Phänomen der Osmose besteht im Bestreben eines reinen Lösungsmittels, durch eine semipermeable Membran in eine Lösung hineinzuwandern. Als osmotischen Druck Π bezeichnet man denjenigen Druck, den man auf die Lösung ausüben muss, um das Eindringen der Lösungsmittelteilchen zu verhindern.“[20]

Ursprünglich wurde unter Osmose „die partielle Diffusion einzelner Komponenten von Flüssigkeitsgemischen durch poröse Wände“[21] verstanden, was Lösungsmittel und gelöste Stoffe gleichermaßen einschließt.[22] Pfeffer spricht in diesem Zusammenhang von der Diosmose gelöster Körper.[10] Van’t Hoffs 1887 erschienene Grundlagenarbeit zum osmotischen Druck machte das Konzept einer ideal semipermeablen Membran, die als ausschließlich für das Lösungsmittel durchlässig angenommen wird, zum Dreh- und Angelpunkt für die theoretische Darstellung der Osmose.[23] Dagegen sind reale Membranen immer bis zu einem gewissen Grad für gelöste Stoffe durchlässig; wieweit kann mittels des substanzabhängigen Reflexionskoeffizenten σ angegeben werden.[24] Für Reflexionskoeffizenten 1 > σ_i > 0, wird die Membran als leaky membrane (englisch: undichte Membran) bezeichnet.[25][26]

Für die quantitative Beschreibung osmotischer Systeme ist eine qualitative Unterscheidung zwischen Lösungsmittel und gelöstem Stoff nicht erforderlich.[27] Phänomene wie der Gibbs-Donnan-Effekt beruhen darauf, dass neben dem Lösungsmittel auch gelöste Ionen die Membran passieren.[28] Die Dialyse, bei der neben dem Lösungsmittel auch andere, gelöste Substanzen durch die Membran diffundieren, wird oft als ein auf Osmose beruhendes Phänomen beschrieben,[28][29] während andere Autoren die Abgrenzung zwischen Osmose (lediglich das Lösungsmittel durchquert die Membran) und Dialyse betonen.[22]

Häufig zu finden sind Definitionen, die ausschließlich Wasser als Lösungsmittel erwähnen. Tatsächlich können bei geeigneter Membranbeschaffenheit auch andere Flüssigkeiten und Gase (Gasosmose) an osmotischen Vorgängen beteiligt sein.[30]

Sehr oft wird Osmose als eine durch Diffusion verursachte Bewegung über eine semipermeable Membran beschrieben; diese Erklärung geht auf einen Vorschlag des Physiologen Adolf Fick aus dem Jahr 1855 zurück.[31] Tatsächlich ist der osmotische Fluss durch Membranporen ein konvektiver Vorgang („convective“ oder auch „non-diffusional flow“), der nicht den Fick’schen Diffusionsgesetzen gehorcht;[32] siehe auch Membrantechnik#Stofftransport.

Von Thermoosmose spricht man, wenn der Stofffluss aufgrund eines Temperaturunterschieds erfolgt.[33][34] Elektroosmose bezeichnet die Bewegung einer Flüssigkeit entlang einer elektrochemischen Doppelschicht.

Grundlagen

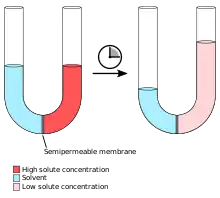
Osmose: links ein U-Rohr mit verschieden konzentrierten Lösungen unmittelbar nach dem Einfüllen, rechts dasselbe U-Rohr zu einem späteren Zeitpunkt. Das Gleichgewicht ist erreicht, wenn der hydrostatische Druck der rechten Flüssigkeitssäule dem osmotischen Druck der Lösung entspricht.

Bei der Osmose kann ein Konzentrationsunterschied zwischen beiden Seiten nur durch den Fluss der Substanzen ausgeglichen werden, die aufgrund ihrer Eigenschaften die Membran passieren können. In vielen Fällen ist dies das Lösungsmittel, z. B. Wasser in biologischen Systemen.

Wie im Beispiel rechts dargestellt, fließt Wasser von der Seite der geringeren Konzentration (in der Abb. die linke Hälfte des U-Rohrs) durch die Membran; seine Menge nimmt dort ab und führt zu einer entsprechenden Volumenvergrößerung auf der anderen Seite. Die Bewegung des Lösungsmittels endet, sobald sich auf beiden Membranseiten ein gleich großes chemisches Potential eingestellt hat. In der Abbildung ist es der hydrostatische Druck der rechten Flüssigkeitssäule, der dem weiteren Fluss von Lösungsmittel entgegenwirkt.

Wird nach Erreichen des Gleichgewichtszustands das Wasser einer Seite mit D₂O (schweres Wasser) oder ³H₂O (überschweres Wasser) markiert, so lässt sich zeigen, dass weiter ein Austausch von Wassermolekülen erfolgt.[35] Im Gleichgewicht ist jedoch die Menge der einströmenden und ausströmenden Moleküle auf beiden Seiten gleich.

Thermodynamische Betrachtung

Die spontan verlaufende Osmose beinhaltet einen Mischungsvorgang – ein Stoff tritt aus einer Phase in die andere über und vermischt sich dort mit den vorhandenen Komponenten. Freiwillig ablaufende Mischungsvorgänge führen in abgeschlossenen Systemen zu einer Verringerung der freien Enthalpie (Gibbsche Energie) und zu einer Vergrößerung der Entropie. Im Fall der Osmose verhindert die selektiv durchlässige Membran als Barriere, dass mit Erreichen des thermodynamischen Gleichgewichts sämtliche Konzentrationsunterschiede verschwinden; es sind zu jedem Zeitpunkt zwei getrennte Phasen vorhanden. (Tatsächlich drei Phasen, wenn die Membran in die Betrachtung mit einbezogen wird.)

Die Gesamtänderung der freien Enthalpie in der osmotischen Zelle muss daher als die Summe der Änderungen in beiden Phasen geschrieben werden:

\mathrm {d} G=\mathrm {d} G^{(1)}+\mathrm {d} G^{(2)}\

wobei das Superskript ^(x) den jeweiligen Abschnitt $x$ der osmotischen Zelle bezeichnet. Wenn nur eine Stoffart $L$ (z. B. das Lösungsmittel) von der Membran durchgelassen wird, kann der Zusammenhang zwischen freier Enthalpie $G$ und Änderung der Stoffmenge $\mathrm {d} n_{L}$ durch

\mathrm {d} G^{(1)}=\mu ^{(1)}\mathrm {d} n_{L}

und

\mathrm {d} G^{(2)}=\mu ^{(2)}\mathrm {d} n_{L}

beschrieben werden, wobei $\mu$ das chemische Potential bezeichnet und $n$ die Stoffmenge des Stoffes, der die Membran passiert. Da der Zufluss von $L$ auf Seite ⁽²⁾ dem Verlust auf Seite ⁽¹⁾ entspricht (Erhaltungsbedingung), folgt für die gesamte Änderung der freien Enthalpie:

\ \mu ^{(2)}\mathrm {d} n_{L}=-\mu ^{(1)}\mathrm {d} n_{L}

und somit

\mathrm {d} G=(\mu ^{(1)}-\mu ^{(2)})\mathrm {d} n_{L}

Solange das Gleichgewicht noch nicht erreicht ist ( $\mathrm {d} G\leq 0$ ), gilt für die chemischen Potentiale:

\mu ^{(1)}>\mu ^{(2)}

und im Gleichgewicht ( $\mathrm {d} G=0$ ):

\mu ^{(1)}=\mu ^{(2)}

.

Nimmt mehr als eine Stoffart am osmotischen Prozess teil, müssen obenstehende Relationen um die chemischen Potentiale der zusätzlichen Komponenten erweitert werden (siehe auch Abschnitt Das osmotische Potential nichtidealer Lösungen).

Die Bedingung für das osmotische Gleichgewicht ist, dass die chemischen Potentiale der von der Membran durchgelassenen Stoffe (meist das Lösungsmittel) in beiden Phasen gleich sind. Solange noch eine Potentialdifferenz besteht, werden sich Teilchen der jeweiligen Komponente in Richtung des niedrigeren Potentials bewegen. Andererseits kann durch Erhöhen des chemischen Potentials, etwa durch Anwendung von Druck oder eine Temperatursteigerung auf einer Seite der Membran, die Bewegungsrichtung umgekehrt werden. Osmose durch eine Membran, im Gegensatz zur Diffusion in einem einphasigen System, ist ein reversibler Vorgang.[23]

Lösungseffekt als unmittelbare Ursache

Durch den Lösungseffekt verringert sich das chemische Potential des Lösungsmittels in der Lösung gegenüber dem reinen Stoff, verbunden mit einer Erniedrigung des Sättigungsdampfdrucks bei Flüssigkeiten oder des Partialdrucks bei Gasen. Damit ist der Lösungseffekt eine unmittelbare Ursache für Osmose.

Dagegen wirkt ein Konzentrationsgefälle der gelösten Stoffe mittelbar, da nur, wenn die Konzentrationsunterschiede zu einer Differenz des chemischen Potentials des Lösungsmittels in beiden Lösungen führen, Osmose stattfindet. Sind auf beiden Seiten der Membran unterschiedliche Stoffe in gleicher Teilchenzahl gelöst, so ist das chemische Potential des Lösungsmittels gleich und es tritt somit keine Osmose auf. Darauf beruht die Wirkung der Osmolyte, mit denen sich Zellen gegen osmotischen Druck schützen können.[36]

Molekularkinetische Betrachtung

Einen Ansatz zur Erklärung der Osmose mit den Mitteln der statistischen Mechanik lieferte Albert Einstein 1905 in seiner Arbeit Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Lösungen suspendierten Teilchen. Darin beschreibt er, dass sich suspendierte von „eingelösten“ Teilchen lediglich durch ihre Größe unterscheiden und beide daher nach der molekularen Theorie der Wärme einen osmotischen Druck hervorrufen. Nach Einstein wirkt auf suspendierte Teilchen eine Kraft, die mit den osmotischen Druckkräften in dynamischem Gleichgewicht steht; die Bewegung kann als Überlagerung zweier Prozesse aufgefasst werden: Einer Bewegung der suspendierten Teilchen aufgrund einer auf jedes einzelne Teilchen einwirkenden Kraft, sowie „eines Diffusionvorganges als Folge der ungeordneten Molekularbewegung der Wärme.“[15]

Osmose und Mischungsentropie

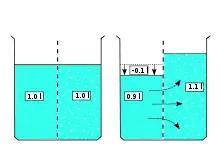
Links der Membran das Lösemittel, rechts die Lösung. Das Einströmen von Lösemittel in die Lösung (rechtes Bild) erhöht die Anzahl der räumlichen Anordnungsmöglichkeiten, für das Lösemittel wie auch für die gelösten Moleküle. Der umgekehrte Vorgang einer spontanen Entmischung ist extrem unwahrscheinlich, kann aber durch Anwendung von Druck erzwungen werden (Umkehrosmose).

Osmose – als Diffusion des Lösemittels durch eine Membran in eine Lösung – ist ein spontaner Mischungsvorgang. Allgemein hat eine Mischung zweier Flüssigkeiten A und B eine höhere Entropie als die beiden getrennten Substanzen, da im gemeinsamen und damit größeren Volumen mehr Positionen zur Verfügung stehen, an denen sich jedes Teilchen A oder B aufhalten kann. Damit gibt es auch für jede der beiden Komponenten eine größere Zahl von Anordnungsmöglichkeiten (Mikrozustände) als in den Teilvolumina der getrennten Substanzen, so dass dieser weiträumige Makrozustand am wahrscheinlichsten ist. Er stellt sich von selbst ein durch die thermische Bewegung der Moleküle. Das Maß für die Wahrscheinlichkeit ist die Entropie und deshalb hat sie bei dieser Verteilung auch ihr Maximum. Das Lösemittel, in vielen praktisch wichtigen Fällen Wasser, das durch die selektiv durchlässige Membran diffundiert, mischt sich mit den gelösten Molekülen. Die Entropie des Gesamtsystems erhöht sich um diese Mischungsentropie (es gibt jedoch keine Mischungsentropie Wasser/Wasser Gibbssches Paradoxon). Im Rechenbeispiel erhält man mit 0,001 mol gelöster Substanz und 0,1 Liter Wasser, das durch die Membran diffundiert, eine Mischungsentropie von ≈ 0,08 J K⁻¹. Zu diesem Ergebnis kommt man auf zwei Wegen. Einmal über die Stoffmengenanteile und die mittlere molare Mischungsentropie[37] oder über das statistische Gewicht des Mischungszustands:

Thermodynamisch

Molmengen $n$ und Stoffmengenanteile $x$ :

	$n$	$x$
(1) gelöste Substanz	0,001 mol	1,80653·10⁻⁴
(2) Wasser	5,53446 mol	0,999819

Mittlere molare Mischungsentropie: ${\overline {\Delta S_{\mathrm {mix} }}}=-R\cdot \left[x_{1}\cdot \ln(x_{1})+x_{2}\cdot \ln(x_{2})\right]=0{,}0144477\;\mathrm {J\,K} ^{-1}\,\mathrm {mol} ^{-1}$

Das ergibt für 5,53546 mol (also die gesamte Molmenge): $\Delta S_{\mathrm {mix} }=0{,}07997\;\mathrm {J\,K} ^{-1}$

Statistisch

( $N$ bedeutet die Zahl der Moleküle)

\Delta S=k_{\mathrm {B} }\cdot \ln W\quad {\text{mit}}\quad W={\frac {(N_{1}+N_{2})!}{N_{1}!\cdot N_{2}!}}\quad {\text{also}}\quad W={\frac {(5{,}53546\cdot 6{,}02205\cdot 10^{23})!}{(0{,}001\cdot 6{,}02205\cdot 10^{23})!\cdot (5{,}53446\cdot 6{,}02205\cdot 10^{23})!}}

Mit der Näherung $\ln(N!)\approx N\cdot \ln N$ erhält man für die Mischungsentropie: $\Delta S=0{,}07997\;\mathrm {J\,K} ^{-1}$

Osmotischer Druck

Analogie zum Gasdruck

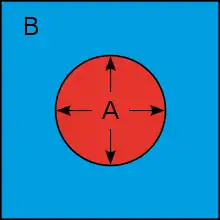
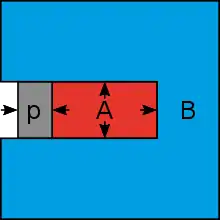
Abb. 1 Osmotischer Druck im Gleichgewicht

Abb. 2 Ausgleich des osmotischen Drucks mittels eines Kolbens

Wird ein mit Zuckerlösung (A) gefülltes Gefäß in reines Wasser (B) gebracht, und ist seine Wand nur für die gelösten Zuckermoleküle undurchlässig, so wird sich durch das Einströmen von Wasser der Druck im Innenraum erhöhen. Der so erzeugte osmotische Druck wirkt dem Wassereinstrom entgegen; die Bewegung des Wassers endet mit Erreichen des Gleichgewichts (Abb. 1). Die gleiche Druckverteilung wie in Abb. 1 kann ohne Wassereinstrom erreicht werden, wenn (z. B. über einen Kolben) ein gleich großer Druck auf die Flüssigkeit (A) wirkt. (Abb. 2). Durch Erhöhen oder Verringern des Kolbendrucks verändert sich die Konzentration der Lösung (A), da dann Wasser durch die Gefäßwände entsprechend aus- oder einströmt. Dieses Prinzip wird bei der Umkehrosmose (in älteren Schriften auch als Anti-Osmose bezeichnet) eingesetzt; dabei wird unter Druck eine Lösung weiter aufkonzentriert, um die darin gelösten Stoffe zu entfernen.

Diese grundlegende Analogie zwischen osmotischem und Gasdruck wurde zuerst 1887 von dem niederländischen Chemiker van ’t Hoff beschrieben.[23] Als Ursache des osmotischen Drucks sah er die Stöße der gelösten Teilchen auf die (für sie undurchlässige) Membranwand (Solute bombardment theory)[3] an. Der Einfluss der Wassermoleküle sei dagegen auf beiden Membranseiten gleich und würde sich daher gegenseitig aufheben. Gegen diese Interpretation spricht, dass keine Durchbiegung der Membran beobachtet wird, wenn der hydrostatische Druck auf beiden Seiten gleich ist.[27][38]

Anwendung der Gasgesetze

In verdünnten flüssigen Lösungen gelten dieselben Gesetze wie für ideale Gase (Boyle-Mariotte-Gesetz, Gay-Lussac-Gesetz, Avogadro-Gesetz). Der osmotische Druck

ist proportional zu der molaren Konzentration des gelösten Stoffes
ist proportional zur absoluten Temperatur
von Lösungen hängt nur von der Teilchenzahl des gelösten Stoffes (molaren Konzentration) ab (→ kolligative Eigenschaft)
einer Lösung von 1 mol in 22,4 l Lösungsmittel beträgt bei 273,15 K (0 °C) 101,325 kPa (Standarddruck)

Diese Aussagen werden zusammengefasst durch das van-’t-Hoff’sche Gesetz „der osmotische Druck ist ebenso groß wie der Druck eines Gases gleicher Teilchendichte $n$ und Temperatur $T$ “:

\Pi ={\frac {n}{V}}\cdot i\cdot R\cdot T=c\cdot i\cdot R\cdot T

Hierbei ist

$\Pi$ der osmotische Druck
c = n/V die Stoffmengenkonzentration (molare Konzentration) der Lösung
i = Van-’t-Hoff-Faktor (Anzahl der im Wasser dissoziierenden Teilchen pro Molekül (z. B. $i=1$ für Glucose; $i=2$ für NaCl))
$R$ die universelle Gaskonstante
$T$ die absolute Temperatur in K.

In dieser Form gilt das Gesetz nur für verdünnte Lösungen (< 0,1 mol/l), ebenso wie die idealen Gasgesetze nur bei niedrigen Drücken gelten (die Wechselwirkung der Teilchen miteinander werden vernachlässigt).

Osmotischer Druck und Dampfdruck

Der Dampfdruck einer Lösung ist immer niedriger als der des reinen Lösungsmittels $L$ (Lösungs- oder Verdünnungseffekt). Das Hinzufügen eines Stoffes zu $L$ erniedrigt dessen chemisches Potential

\Delta \mu _{L}=RT\ln \left({\frac {P_{L}}{P_{\dot {L}}}}\right)

.

Dabei ist $P_{L}$ der Dampfdruck des reinen Lösungsmittels und $P_{\dot {L}}$ der Lösung. Der osmotische Druck wirkt entgegengesetzt und führt zu einer Vergrößerung von $\mu _{L}$

\Delta \mu _{L}=\int _{0}^{\Pi }V_{L}^{m}\mathrm {d} P

Für Flüssigkeiten kann das partielle Molvolumen $V_{L}^{m}$ als druckunabhängig angesehen werden. Unter dieser Bedingung kann aus beiden obenstehenden Termen die Gleichung:

V_{L}^{m}\Pi =RT\ln \left({\frac {P_{\dot {L}}}{P_{L}}}\right)

abgeleitet werden. Sie besagt, dass der osmotische Druck dem äußeren Druck entspricht, der den Dampfdruck einer Lösung auf den Dampfdruck des reinen Lösungsmittels $L$ erhöhen würde. Die treibende Kraft der Osmose ist die durch den Lösungseffekt verursachte Dampfdruckerniedrigung des Lösungsmittels. Eine osmotische Zelle befindet sich im Gleichgewicht, wenn der osmotische Druck durch eine gleich große Gegenkraft ausgeglichen wird.

Salzlösungen (Elektrolyte)

Der osmotische Druck einer Salzlösung ist immer höher als es dem van ’t Hoffschen Gesetz in der Form Π = c⋅R⋅T entspricht, und zwar häufig doppelt oder dreifach so hoch. Dieser Effekt beruht darauf, dass Salze beim Lösungsvorgang in negativ und positiv geladene Ionen zerfallen (→ Dissoziation) und gelöst eine höhere Teilchenzahl aufweisen, als der Stoffmenge im festen Zustand entspricht. Für vollständig gelöste Salze (starke Elektrolyte) ist dies ein ganzzahliges Vielfaches der ursprünglichen Stoffmenge. Durch Erweiterung der Gleichung um einen Faktor:

\Pi =i\cdot c\cdot R\cdot T

kann dieser Effekt berücksichtigt werden. Hierbei ist $i$ der Van-’t-Hoff-Faktor, eine dimensionslose Zahl. Für Natriumchlorid (NaCl), Kaliumchlorid (KCl) und andere binäre Elektrolyte ist $i=2$ ; für 1,2-wertige Elektrolyte wie Natriumsulfat (Na₂SO₄) ist $i=3$ .

Für Salze, die in Lösung nicht vollständig zerfallen (schwache Elektrolyte), kann der Van-’t-Hoff-Faktor aus dem Dissoziationsgrad $\alpha$ berechnet werden:

i=1-\alpha +\nu \alpha

wobei $\nu$ die Anzahl der Ionen pro Salzmolekül ist. Deshalb kann es bei der Konzentrationsangabe von Ionen sinnvoll sein, diese in den Maßeinheiten osmol·l⁻¹ (Osmolarität) bzw. osmol·kg⁻¹(Osmolalität) anzugeben, da hier die Dissoziation bereits beachtet wird.

Das osmotische Potential nichtidealer Lösungen

Das van ’t Hoffsche Gesetz gilt nicht für Lösungen, bei denen die Wechselwirkung der Moleküle nicht mehr vernachlässigt werden kann. Hier muss das chemische Potential aus der Gibbsschen Fundamentalgleichung verwendet werden. Im thermodynamischen Gleichgewicht ist die freie Enthalpie (Gibbs-Energie) einer osmotischen Zelle minimal:

\mathrm {d} G=V\cdot \mathrm {d} p-S\cdot \mathrm {d} T+\sum _{i=0}^{N}\mu _{i}\cdot \mathrm {d} n_{i}=0

Bei konstanter Temperatur vereinfacht sich die Gleichung zu:

0=V\cdot \mathrm {d} p+\sum _{i=0}^{N}\mu _{i}\cdot \mathrm {d} n_{i}

Bei konstantem Umgebungsdruck folgt für die Änderung des osmotischen Drucks:

\mathrm {d} \Pi =-\sum _{i=0}^{N}\mu _{i}\cdot \mathrm {d} c_{i}

.

Der osmotische Druck $\Pi$ ergibt sich somit mit den molaren Dichten $c_{i}$ aus der Veränderung aller chemischen Potentiale $\mu$ . In dieser Gleichung sind Mischungseffekte der beteiligten Substanzen berücksichtigt. Meist jedoch werden die Mischungseffekte der gelösten Stoffe untereinander und die Konzentration des Lösungsmittels vernachlässigt:

\Pi =-RT\cdot \sum _{i=1}^{N}\Delta \left(c_{i}\cdot \ln a_{i}\right)

.

Eine weitere Näherung wäre die Vernachlässigung des Mischungseffektes des gelösten Stoffes mit dem Lösungsmittel. Hierbei wird die Aktivität $a_{i}$ dieser Stoffe als eins angenommen, so dass sich als grobe Näherung ergibt:

\Pi \approx -RT\cdot \sum _{i=1}^{N}\Delta c_{i}

.

Diese überschlägige Berechnung kann für verdünnte Lösungen verwendet werden, führt jedoch bei höheren Konzentrationen zu Fehlern von mehr als 50 %, insbesondere, da hier der Lösungseffekt nicht berücksichtigt wird.

Der negative Wert des osmotischen Drucks wird als osmotisches Potential $\psi _{o}$ bezeichnet.

Der osmotische Koeffizient und die Ionenstärke

Es existieren verschiedene Definitionen zum osmotischen Koeffizienten.

Der osmotische Koeffizient $f_{o}$ ist z. B. definiert als Quotient von real gemessenem osmotischem Druck und theoretisch erwartetem (berechnetem) osmotischem Druck (zu dieser Konzentration) einer Salzlösung oder nichtionischen Lösung (molekularer Substanzen):[39]

f_{o}={\frac {\Pi _{\text{gemessen}}}{\Pi _{\text{berechnet}}}}

Realverdünnte Lösungen hätten daher immer einen Wert kleiner oder gleich Eins.

Empirisch konnte folgender Zusammenhang aufgezeigt werden:[40]

f_{o,(c,z,I)}={1-K\cdot {\sqrt {I}}}

$K$ ist hier eine Konstante, $I$ die Ionenstärke. Die Debye-Hückel-Theorie führte für verdünnte Elektrolyt-Lösungen zu folgender theoretischen Gleichung:[41]

f_{o,(c,z,I)}={1-(2{,}303/3)\cdot A\cdot z_{+}\cdot z_{-}{\sqrt {I}}}

A ist eine Konstante nach der Debye-Hückel-Theorie. Die Ionenwertigkeiten (Ladungszahlen) z sind als Beträge einzusetzen. Diese Gleichung bestätigte die empirisch gefundene erste Gleichung.

Dieser osmotische Koeffizient wird unter anderem in der Elektrochemie benutzt. Der Koeffizient sagt etwas aus über die Abweichung/Nähe vom/zum Idealzustand (ideale Verdünnung bei c=0 mol/liter oder genauer Ionenstärke I=0 mol/liter) einer Lösung. Idealverdünnte Lösungen haben einen osmotischen Koeffizienten des Wertes Eins - nach dieser Definition. Bei hohen Konzentrationen (genauer: Ionenstärken) strebt der Wert gegen Null. Daher bestehen Analogien zum Dissoziationsgrad und zum Leitfähigkeitskoeffizienten der elektrolytischen Leitfähigkeit, denn auch diese Werte laufen von (theoretisch) Null (hohe Konzentration c oder Ionenstärke I) bis Eins (Idealverdünnung, c=0, I=0).

Die Ionenstärke I, die von Gilbert N. Lewis und Merle Randall 1921 definiert wurde, soll ebenfalls ein Maß für die Abweichung einer Elektrolytlösung vom Idealzustand sein (gemeint ist offenbar der Vergleich mit dem arithmetischen Mittel der molaren Konzentrationen).[42] Für binäre Elektrolyte (ein Kation und ein Anion) ist die Ionenstärke I als arithmetisches Mittel der quadratisch nach den Ionenwertigkeiten (Ladungszahlen) gewichteten Konzentrationen anzusehen.

Osmometrie – Messung des osmotischen Drucks

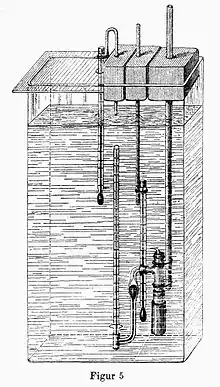
Pfeffersche Zelle – Prototyp des Membranosmometers[10]

Der osmotische Druck einer Lösung wird mit Membranosmometern ähnlich der Pfefferschen Zelle bestimmt. Dabei kann der Druck entweder statisch, nach Einstellung des Gleichgewichts, gemessen werden oder dynamisch, indem an das Steigrohrmanometer ein äußerer Druck angelegt wird, der den osmotischen Fluss gerade unterbricht.

Eine 1 molale Lösung von Rohrzucker (molare Masse 342,30 g·mol⁻¹) in Wasser bewirkt bei Raumtemperatur bereits einen osmotischen Druck von 2,70 MPa (27 bar). Für erheblich höhere Drücke (mehrere 100 bar) lassen sich Messprinzipien wie die Änderung des Brechungsindex von Wasser oder der piezoelektrische Effekt einsetzen.[28]

Durch Messung des osmotischen Drucks beziehungsweise Potentials ist es möglich, die mittlere Molekülmasse von Makromolekülen zu bestimmen; dieses Verfahren wird als Osmometrie bezeichnet. Da zwischen dem osmotischen Druck und den anderen kolligativen Eigenschaften einer Lösung, dies sind Siedepunktserhöhung und Gefrierpunktserniedrigung, ein unmittelbarer Zusammenhang besteht, kann durch deren Messung indirekt der osmotische Druck als osmotischer Wert ermittelt werden.

Während die direkte Messung des osmotischen Drucks die Anwesenheit zweier Phasen und einer spezifisch permeablen Membran erfordert, benötigen die indirekten Verfahren der Osmometrie lediglich die zu messende Lösung. Sie eignen sich daher besonders gut für die Charakterisierung unterschiedlicher Lösungen hinsichtlich ihrer osmotischen Eigenschaften. Osmolarität und Osmolalität geben die Konzentration gelöster Teilchen bezogen auf das Volumen oder die Stoffmenge an. Isoosmotisch sind Lösungen, deren osmotischer Wert gleich ist. Da der osmotische Wert keine Aussage über die Komponenten in den miteinander zu vergleichenden Lösungen beinhaltet, kann isoosmotisch nicht mit isotonisch gleichgesetzt werden.

Die selektiv permeable Membran

Wesentliches Element der Osmose ist die selektiv durchlässige (permeable) Membran; sie bestimmt, welche Stoffe passieren können. Durch diese Eigenschaft wird der erreichbare Gleichgewichtszustand des Systems festgelegt. Zugleich beeinflusst sie über die Diffusionsgeschwindigkeit der durchgelassenen Stoffe das dynamische Verhalten des Systems.[5]

Traubesche und Pfeffersche Zelle

Künstliche Membranen erzeugte zuerst der Privatgelehrte Moritz Traube aus Kaliumhexacyanidoferrat(II) (gelbes Blutlaugensalz), das in verdünnter Kupfersulfatlösung eine Haut aus Kupfercyanoferrat(II) (siehe auch Kupfer-Nachweis) bildet. Diese ist nur für Wasser durchlässig. Das durch Osmose einströmende Wasser zerreißt die Haut, wodurch das eingeschlossene Kaliumhexacyanoferrat(II) wieder freigesetzt wird und sich erneut osmotische Zellen bilden, die nach einiger Zeit wiederum zerreißen.[43] Ähnlich verhalten sich Salze von Erdalkali- und Schwermetallen in Alkalisilikatlösungen. Die dabei entstehenden Gebilde sind unter der Bezeichnung osmotischer oder chemischer Garten bekannt.[44]

1877 gelang es Wilhelm Pfeffer, diese mechanisch instabilen Niederschlagsmembranen auf das poröse Wandmaterial von Tonzellen aufzubringen und sie so zu stabilisieren. Er benutzte die Pfeffersche Zelle als Osmometer und konnte so den osmotischen Druck erstmals quantitativ bestimmen.

Mechanismen der Selektivität

Osmose durch eine semipermeable Membran. Die größeren roten Teilchen können die Poren der Membran nicht durchdringen.

Bei dem in der Abb. rechts dargestellten Membranmodell resultiert die selektive Durchlässigkeit aus der maximalen Porenweite. Die größeren roten Teilchen können die Membran nicht passieren, während die kleineren blauen Teilchen ungehindert von einer Seite zur anderen wechseln. Die für die Osmose entscheidende selektive Permeabilität kann aber auch auf anderen Mechanismen beruhen. In vielen Fällen spielen Lösungsvorgänge eine Rolle, so bei der von Nollet verwendeten Schweinsblase.

Auch katalytische Eigenschaften des Membranmaterials können für die selektive Permeabilität verantwortlich sein. Wenn ein Gemisch von Stickstoff (N₂) und Wasserstoff (H₂) durch eine dünne Folie aus Palladium von reinem Stickstoff getrennt wird, tritt Osmose auf; der Wasserstoff bewegt sich zu der wasserstoffärmeren Seite. Die Wasserstoff-Moleküle werden an der Palladiumoberfläche katalytisch in atomaren Wasserstoff gespalten, der anschließend durch die Palladiumfolie diffundiert.[28]

Letztlich kann selektive Permeabilität an Grenzflächen auftreten, die keine Membranen im engeren Sinne sind. Ein Beispiel dafür ist die Elektroosmose.

Osmose in der Biologie

Die Osmose hat eine besondere Bedeutung für biologische Systeme. Jede Zelle ist von einer Membran umgeben, die eine Barriere für den ungehinderten Stofftransport darstellt, für das Lösungsmittel Wasser aber durchlässig ist. Zugleich besitzt sie mehrere Zellorganellen mit selektiv permeablen Membranen. Viele Zellen stehen im Austausch mit Wasser, insbesondere Pflanzenzellen, die für die Aufnahme, den Transport und die Abgabe von Wasser zuständig sind. Zellen von Wirbeltieren sind von Blut und Lymphe umgeben.

Biomembranen

Osmose bei einer gefärbten Zelle

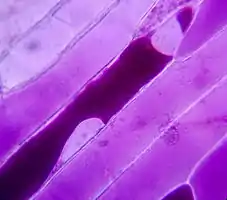
Biomembranen sind für zahlreiche Stoffe selektiv durchlässig. Die Trägersubstanz einer Biomembran ist die Lipiddoppelschicht; sie ist nahezu undurchlässig für Wasser und darin gelöste Substanzen. Eingebettet in die Lipidschicht sind zahlreiche Transmembranproteine, die auf unterschiedliche Weise den Transport von Wasser und gelösten Teilchen durch die Membran hindurch ermöglichen. Zu den passiven gehören, neben porenbildenden Proteinen wie Ionenkanälen und Aquaporinen (Wasserkanäle), sogenannte Cotransporter. Aktiv arbeitende Transportproteine wie Protonenpumpen befördern Substanzen unter Verbrauch von Energie (meist aus der Hydrolyse von Adenosintriphosphat gewonnen) gegen ein vorhandenes Konzentrationsgefälle. Die Tätigkeit dieser Proteine kann das chemische Potential des Lösungsmittels Wasser inner- und außerhalb der Zelle oder seiner Organellen aktiv beeinflussen.

Die Durchlässigkeit oder Transportrate zahlreicher passiver Membranproteine kann durch zelluläre Mechanismen reguliert werden (zum Beispiel dem Gating von Ionenkanälen); dadurch ist es der Zelle möglich, auf Änderungen des umgebenden Milieus zu reagieren und so den osmotischen Stofftransport zu beeinflussen.

Wasserpotential

Zur Beschreibung des Wasserhaushalts von biologischen Systemen hat sich das Konzept des Wasserpotentials als nützlich erwiesen. Es beschreibt den Saugwert einer Lösung für Wasser. Es werden lediglich Potentialdifferenzen betrachtet, das Wasserpotential von reinem Wasser hat bei Standardbedingungen den Wert 0. Für das Wasserpotential einer Lösung gilt:

\Psi =p-\Pi +g\cdot h\cdot \rho _{\mathrm {H_{2}O} }

$\Psi$ hat die Dimension Energie · Volumen⁻¹ oder Kraft · Fläche⁻¹ und wird in der Einheit Pascal angegeben.

In obenstehender Gleichung ist $p$ der hydrostatische Druck, $-\Pi$ das osmotische Potential sowie der Ausdruck $g\cdot h\cdot \rho _{\mathrm {H_{2}O} }$ das Gravitationspotential, das bei der Betrachtung einzelner Zellen vernachlässigt werden kann.[45]

Das Wasserpotential einer Lösung ist somit die Summe mehrerer Teilpotentiale. Dabei beschreibt das osmotische Potential $\psi _{o}=-\Pi$ den Anteil des osmotischen Drucks am Saugwert der Lösung.

Wassertransport in Pflanzen

Pflanzen befördern Flüssigkeiten aus dem Wurzelbereich bis in die Spitzen. Durch die Osmose wird der sogenannte Wurzeldruck aufgebaut, der zusammen mit dem Transpirationssog und den Kapillarkräften die benötigte Druckdifferenz zum Wassertransport gegen die Schwerkraft bereitstellt. Bei diesem Transportprozess dominiere nach der nach weithin akzeptierten Kohäsionstheorie[46] der Transpirationssog, da dieser deutlich höhere Drücke als der Wurzeldruck erreiche. Osmose bzw. der osmotische Druck, mithin der Gradient des Wasserpotenzials ist für den Wassertransport über große Höhenunterschiede ausreichend. In[47] wird belegt, dass die Transpirationsthese für den Wassertransport in Pflanzen über große Höhenunterschiede nicht konsistent ist.

Osmoregulation

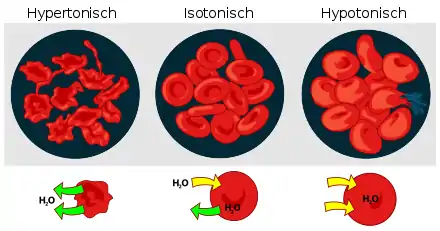
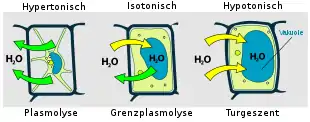
Wirkung des osmotischen Drucks auf Erythrozyten

Osmotische Zustände einer Pflanzenzelle (Plasmolyse)

Wird die osmotische Resistenz roter Blutkörperchen durch Einbringen in destilliertes Wasser (stark hypotones Medium) überschritten, nehmen sie unkontrolliert Wasser auf, bis sie schließlich platzen. Ihre Zellmembranen können nur einem geringeren Druck standhalten. Pflanzenzellen dagegen sind von einer stützenden Zellwand umgeben, wodurch sie erheblich höhere Innendrücke (→ Turgor) aushalten.

Zahlreiche Organismen wie Salzpflanzen, Halophile sowie Süßwasserbewohner leben in Umgebungen, deren osmotischer Wert stark von dem im Körper- oder Zellinneren abweicht. Ohne wirksame Osmoregulation würde der Organismus entweder austrocknen oder unkontrolliert Wasser aufnehmen.

In Süßwasser lebende Einzeller verfügen über eine kontraktile Vakuole, die zunächst Wasser aus dem Cytoplasma aufnimmt und es danach aus der Zelle hinausschleust. Halophile (Salzbewohner) haben eine Reihe von Strategien entwickelt, um mit dem Salzüberschuss umzugehen. Dazu gehört die Ausbildung spezieller Organe wie Salzdrüsen oder Nieren zur Salzausscheidung, Mechanismen zur Salzeinlagerung oder die Anreicherung osmotisch aktiver Substanzen (Osmolyte) in den Zellen.

Nieren finden sich auch bei allen Wirbeltieren. Sie dienen der Ausscheidung sogenannter harnpflichtiger Substanzen, darunter überschüssige Elektrolyte und Glucose, die sonst zu einem Ansteigen des osmotischen Werts im Körper führen würden.

In Säugetierzellen wurde das Protein NFAT5, (ein Transkriptionsfaktor, auch bekannt als Tonicity-Responsive Enhancer Binding Protein, TonEBP) gefunden, das verstärkt exprimiert (synthetisiert) wird, wenn der osmotische Druck ansteigt. Es setzt eine Reihe von Gegenregulationsmechanismen in Gang, um die Zelle vor hypertonem Stress zu schützen. Dazu gehört die Anreicherung von Osmolyten in der Zelle. Beispiele für solche Substanzen sind myo-Inositol, Betain und Taurin, für die jeweils eigene Transportproteine existieren.[36]

Innerhalb von Pflanzenzellen können Chloroplasten große Mengen von Glukose speichern, ohne durch osmotische Belastung zu platzen, indem sie viele Glukose Moleküle zu Stärke Moleküle kondensieren.[48]

Osmotische Arbeit

Im Experiment mit dem U-Rohr (siehe Abschnitt Grundlagen) wurde die rechte Flüssigkeitssäule gegen die Schwerkraft angehoben. Das zeigt anschaulich, dass in einer osmotischen Zelle Arbeit verrichtet werden kann.

Das Konzept der Energiegewinnung durch osmotische Arbeit wird als Osmosekraftwerk bezeichnet, siehe auch Abschnitt Anwendungen und Beispiele.

In den Biowissenschaften und der Medizin wird unter osmotischer Arbeit[49] (engl. osmotic work) oft die Energiedifferenz zwischen den osmotischen Potentialen eines Systems (zum Beispiel einer Zelle) verstanden. In diesem Sinne verrichtet die Zelle osmotische Arbeit, wenn Stoffe aktiv, unter Energieverbrauch gegen ein Konzentrationsgefälle transportiert werden. Andererseits kann die, aus der Differenz osmotischer Potentiale resultierende, osmotische Energie von der Zelle für energieverbrauchende Prozesse genutzt werden, beispielsweise bei der chemiosmotischen Kopplung.

Anwendungen und Beispiele

Osmolaritätsmessung, isoosmolare Puffer und Lösungen

Die Bestimmung der Osmolarität von Lösungen mittels osmometrischer Methoden gehört in vielen Bereichen der Biowissenschaften zum Laboralltag. Bei der Arbeit mit lebenden Zellen ist eine isotone Pufferlösung (wie Ringer) oft unabdingbar, um unerwünschte Reaktionen der Zellen durch osmotischen Stress zu vermeiden. Insbesondere bei der Isolation von Protoplasten würde ein hypoosmolarer Puffer die von keiner Zellwand mehr geschützten Zellen platzen lassen. Bei der Herstellung solcher Lösungen im Labor kann zur Kontrolle die tatsächliche Osmolarität gemessen und mit dem erwarteten Wert verglichen werden.

In der Medizin wird für Infusionen eine isotonische Kochsalzlösung eingesetzt, um eine Schädigung der Körperzellen durch osmotischen Druck zu vermeiden. Es handelt sich dabei um ein Gemisch aus Wasser mit 0,9 % (Massenprozent) Kochsalz, die Osmolarität dieser Lösung entspricht mit 308 mosmol/l annähernd der des Blutplasmas, dies entspricht einem osmotischen Druck von 0,7 MPascal. Würde bei Infusionen reines Wasser anstatt einer isotonen Lösung benutzt werden, könnte ein solcher Druckunterschied die Blutzellen platzen lassen.

Dialyse

Bei der Dialyse werden Membranen eingesetzt, die Moleküle und Ionen unterhalb einer bestimmten Größe oder Molekularmasse durchlassen und Makromoleküle wie Proteine oder Nukleinsäuren zurückhalten. Mit diesem Verfahren können niedermolekulare Substanzen und Ionen gezielt aus einer Lösung entfernt oder deren Konzentration auf den Wert einer vorgegebenen Lösung angeglichen werden. Dazu wird je nach Anwendung die zu dialysierende Lösung in ein geeignetes Gefäß (den Dialyseschlauch) gefüllt und in die äußere Dialyselösung getaucht, worin sie über längere Zeit verbleibt. Oder die zu reinigende Flüssigkeit steht, wie bei der Hämodialyse, über eine semipermeable Membran in Kontakt mit einer Spüllösung. Dialyseverfahren werden in der Medizin unter anderem für die Blutreinigung eingesetzt, sowie in der Chemie und Verfahrenstechnik (zum Beispiel bei der Herstellung von alkoholfreiem Bier).

Dichtegradientenzentrifugation

Bei der Dichtegradientenzentrifugation von lebenden Zellen oder deren Bestandteilen können Stoffe wie Saccharose als Träger des Dichtegradienten oft durch hochmolekulare Substanzen mit nur geringer osmotischer Aktivität (niedriger osmotischer Wert) ersetzt werden, um die Zellen während der Zentrifugation nicht osmotischem Stress auszusetzen.

Umkehrosmose

Bei der Umkehrosmose (auch reverse Osmose oder Antiosmose genannt) wird durch Anwendung von Druck eine Substanz gegen ein Konzentrationsgefälle aufkonzentriert. Dieses Verfahren wird insbesondere für die Aufbereitung (zum Beispiel Entsalzung) von Trinkwasser eingesetzt.

Osmosekraftwerk

Bei dem Konzept des Osmosekraftwerks wird die osmotische Arbeit zur Energiegewinnung eingesetzt. Das Kraftwerk nutzt dazu die Unterschiede im chemischen Potential zwischen salzhaltigem Meer- und Süßwasser aus, um damit Turbinen für die Stromgewinnung zu betreiben. Über eine Membran strömt vorgereinigtes Süßwasser in eine Leitung mit Salzwasser und erhöht so den osmotischen Druck in dieser Leitung. Mit einem Teil des so entstehenden Brackwassers werden Turbinen angetrieben, während der größere Teil (2/3) über einen Druckaustauscher den Druck des frisch zuströmenden Salzwassers erhöht.[50] Osmosekraftwerke sind bislang noch nicht im kommerziellen Einsatz; Prototypen mit einer Leistung von bis zu drei Megawatt werden bereits seit einigen Jahren entwickelt,[51] ein erstes Kleinkraftwerk wurde im November 2009 von Statkraft am norwegischen Oslofjord in Betrieb genommen.[52] Ende 2013 ist Statkraft aus seinem Engagement für Osmosekraftwerke wieder ausgestiegen und begründet dies damit, dass die Technik auf absehbare Zeit nicht kosteneffizient genug für den Wettbewerb auf dem Engergiemarkt sein würde.[53]

Osmose im gasförmigen Aggregatzustand

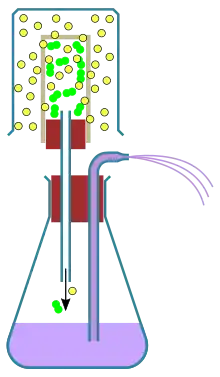
Ein leichtes Gas (Helium; gelbe Kugeln) unter dem Becherglas breitet sich durch die poröse Wand in den mit Luft (grüne Moleküle) gefüllten Tonzylinder hinein aus. Die daraus folgende Druckerhöhung pflanzt sich in den Erlenmeyerkolben fort und bewirkt die Wasserfontäne.

Ein Osmoseversuch kann auch mit Helium bzw. Wasserstoff und Luft durchgeführt werden. Man lässt Helium/Wasserstoff unter ein Becherglas einströmen, das über einen porösen Tonzylinder gestülpt ist. Die Luft darin steht anfangs unter Atmosphärendruck. Die Wand des Tonzylinders bildet für das leichte Gas kein Hindernis, es breitet sich auch in den Zylinder hinein aus und nähert sich so dem wahrscheinlichsten Makrozustand, einer gleichmäßigen Verteilung im Volumen des Becherglases. Die schwereren Moleküle der Luft diffundieren viel langsamer, so dass die eindringenden Atome/Moleküle schnell den Druck erhöhen. Dieser osmotische Druck kann sichtbar gemacht werden, indem man ihn über ein Rohr auf Wasser in einem Erlenmeyerkolben wirken lässt, das dann als Fontäne aus einer Düse spritzt. Ursache ist die spontane Entropievermehrung (Mischungsentropie) im System Becherglas/Tonzylinder. Wird danach das Becherglas entfernt, entsteht im Tonzylinder ein Unterdruck, so dass die durch die Düse einströmende Luft in der Flüssigkeit hochblubbert.

Osmose im Alltag

Bei der Konservierung von Lebensmitteln durch Einzuckern oder Pökeln wird das enthaltene Wasser durch Osmose entzogen, da die Konzentration von Zucker oder Salz außen sehr viel höher als im Inneren des Lebensmittels ist. Vorhandene Mikroorganismen können sich nicht mehr vermehren und daher auch nicht mehr zersetzend wirken. Auf diese Weise haltbar gemachte Lebensmittel verändern sich dabei durch den Wasserentzug oft drastisch.
Beim Kochen von Gemüse wird dem Wasser Salz zugefügt, um den Einstrom von Wasser in das (leicht salzhaltige) Gemüse und den damit verbundenen Geschmacksverlust zu verhindern.
Ein mit Salatsoße angemachter Blattsalat verliert nach relativ kurzer Zeit seine Festigkeit (Turgor). Diese erhält er normalerweise durch das in den Zellen vorhandene Wasser, welches durch Osmose an die Salatsoße abgegeben wird.
Das Aufplatzen reifer Früchte nach einem Regen wird durch den osmotischen Einstrom des Regenwassers und den daraus resultierenden osmotischen Druck im Innern der Frucht bewirkt.

Gesalzene Auberginen

Auberginen werden vor dem Kochen oft mit Salz bestreut. Durch Osmose wird ihnen dabei das Wasser entzogen, und sie werden dadurch beim Anbraten weicher.

Siehe auch

Literatur

Peter W. Atkins, Julio de Paula: Physikalische Chemie. Wiley-VCH, 2005, ISBN 3-527-31546-2.
Luis Felipe del Castillo: El Fenómeno Mágico De La Ósmosis. Fondo De Cultura Economica USA, 2001, ISBN 968-16-5241-X. Umfassende Monografie zum Thema Osmose (spanisch). Online-Ausgabe bei Bibliotheca Digital del ILCE
Walter J. Moore, Dieter O. Hummel: Physikalische Chemie. Walter de Gruyter, Berlin 1986, ISBN 3-11-010979-4.
R. H. Wagner, H. D. Moore: Determination of Osmotic Pressure. In: A. Weissengerber (Hrsg.): Physical Methods of Organic Chemistry. Part 1, 3. Auflage. Interscience, New York 1959.
Gerd Wedler: Lehrbuch der Physikalischen Chemie. Verlag Chemie, 1982, ISBN 3-527-25880-9.
Wilhelm Pfeffer: Osmotische Untersuchungen – Studien zur Zellmechanik. Verlag Wilhelm Engelmann, Leipzig, 1921; archive.org.

Weblinks

Commons: Osmose – Album mit Bildern, Videos und Audiodateien

Wiktionary: Osmose – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Uri Lachish: Osmosis, Reverse Osmosis and Osmotic Pressure – what they are. Abgerufen am 2. November 2019 (englisch).
R.Keller: Fotos eines osmotischen Gartens. Vorlesungssammlung Physik - Universität Ulm. Abgerufen am 2. November 2019.
Video: Osmose und Osmotischer Druck nach Van’t Hoff - Lösemittelmoleküle wandern freiwillig in die konzentriertere Lösung?. Jakob Günter Lauth (SciFox) 2013, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/15678.
Johannes Kottonau: NetLogo-Simulationsmodell für den Unterricht. (Java-Applet) Abgerufen am 2. November 2019.
Physics Videos by Eugene Khutoryansky: Osmosis as you have never seen it. (Simulation) Youtube, 6. November 2021, abgerufen am 20. November 2021.

Einzelnachweise

Siehe z. B. U. Krey, A. Owen: Basic Theoretical Physics – A Concise Introduction. Springer, Berlin 2007, ISBN 978-3-540-36804-5 (relevant für die Statistische Physik und insbesondere für physikalisch-chemische Aspekte ist besonders Teil 4).
O. Kedem, A. Katchalsky: Thermodynamic analysis of the permeability of biological membranes to non-electrolytes. In: Biochim. Biophys. Acta. 27 (1958), S. 229–246. doi:10.1016/0006-3002(58)90330-5
Frank G. Borg: arxiv:physics/0305011v1 What is Osmosis. arXiv.org, e-Print 2003.
David C. Guell, Howard Brenner: Physical Mechanism of Membrane Osmotic Phenomena. 1996 doi:10.1021/ie950787f
A. V. Raghunathan, N. R. Aluru: Molecular Understanding of Osmosis in Semipermeable Membranes. In: Physical Review Letters. Band 97, Nr. 2. American Physical Society, 10. Juli 2006, ISSN 1079-7114, S. 024501-(1–4), doi:10.1103/PhysRevLett.97.024501.
L’Abbé Nollet (Juni 1748): Recherches sur les causes du bouillonnement des liquides. In: Mémoires de Mathématique et de Physique, tirés des registres de l’Académie Royale des Sciences de l’année 1748, S. 57–104
Homer W. Smith, Homer W. Smith: I. Theory of Solutions: A knowledge of the laws of solutions … In: Circulation. Band 21, Nr. 5, Mai 1960, S. 808–817, S. 810, doi:10.1161/01.CIR.21.5.808.
Henri Dutrochet: L’Agent Immédiat du Movement Vital Dévoilé dans sa Nature et dans son Mode d’Action chez les Végétaux et chez les Animaux (Paris: Dentu, 1826), S. 115 und 126.
Henri Dutrochet: Nouvelles Recherches sur l’Endosmose et l’Exosmose, suivies de l’application expérimentales de ces actions physiques à la solution du problême de l’irritabilité végétale. Paris, 1828 (eingeschränkte Vorschau in der Google-Buchsuche).
Wilhelm Pfeffer: Osmotische Untersuchungen – Studien zur Zellmechanik. Engelmann, Leipzig 1877; archive.org.
Harmon Northrop Morse: The Osmotic Pressure of Aqueous Solutions: Report on Investigations Made in the Chemical Laboratory of the Johns Hopkins University During the Years 1899–1913. Carnegie institution of Washington, 1914, S. 222 (archive.org).
J. C. W. Frazer: The Laws of Dilute Solutions. In: H. S. Taylor (Hrsg.): A Treatise on Physical Chemistry. 2. Auflage. Van Nostrand, New York 1931, S. 353–414.
J. H. van ’t Hoff: The role of osmotic pressure in the analogy between solutions and gases. In: Zeitschrift für physikalische Chemie, 1, 1887, S. 481–508 (englisch); Website Uri Lachish. (PDF; 187 kB)
J. H. van ’t Hoff: Osmotical pressure and chemical equilibrium. 1901. Nobel Lecture. (PDF; 40 kB)
Albert Einstein: Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. In: Annalen der Physik, 17, 1905; Universität Wien (PDF; 717 kB)
C.E. Reid, B. Breton: Water and Ion Flow Across Cellulosic Membranes. In: Journal. Applied Polymer Sci. 1, 1959, S. 133–143.
S. Loeb, S. Sourirajan: Sea Water Demineralizationby Means of an Osmotic Membrane. In: Adv. Chem. Ser. 38, 1962, S. 117.
Julius Glater: The early history of reverse osmosis membrane development. In: Desalination. Band 117, Nr. 1, 20. September 1998, S. 297–309, doi:10.1016/S0011-9164(98)00122-2.
Wasserpotential. In: P. Sitte, E. W. Weiler, J. W. Kadereit, A. Bresinsky, C. Körner: Strasburger – Lehrbuch der Botanik. Spektrum Gustav Fischer, 2002, ISBN 3-8274-1010-X, S. 254.
Peter W. Atkins, Julio de Paula: Physikalische Chemie. Wiley-VCH, 2005, ISBN 3-527-31546-2, S. 166.
Kortüm, Lachmann: Einführung in die chemische Thermodynamik. Vandenhoeck & Ruprecht, 1981, S. 245, Fußnote 3.
Sun-Tak Hwang, Karl Kammermeyer: Membranes in separation. (Techniques of chemistry, v. VII). John Wiley & Sons, Rochester, NY 1975, ISBN 0-471-93268-X, S. 24.
J.H. van ’t Hoff: The role of osmotic pressure in the analogy between solution and gases. In: Zeitschrift fur Physikalische Chemie. 1 (1887), S. 481–508 (englisch); Website Uri Lachish. (PDF; 187 kB)
A.J.Staverman: The theory of measurement of osmotic pressure. In: Rec. Trav. Chim. 70, 1951, S. 344.
David Charles Guell: The Physical Mechanism of Osmosis and Osmotic Pressure. A Hydrodynamical Theory for Calculating the Osmotic Reflection Coefficient. Massachusetts Institute of Technology, Cambridge 1991, OCLC 24393943 (englisch, hdl:/1721.1/29859 – Doctoral thesis, Dept. of Chemical Engineering.).
A. E. Hill: Osmosis in Leakey Pores: The Role of Pressure. In: Proc R. Soc. Lond., B 237, 1989, S. 363–367.
Francis P. Chinard, Theodore Enns: Osmotic pressure. In: Science. 124, 1956, S. 472–474.
Moore, Hummel: Physikalische Chemie. Verlag de Gruyter, 1986, ISBN 3-11-010979-4.
Peter W. Atkins, Julio de Paula: Physikalische Chemie. Wiley-VCH, 2005, ISBN 3-527-31546-2, S. 169.
R. Ash, R. M. Barrer, A. Vernon, J. Edge, T. Foley: Thermo-osmosis of sorbable gases in porous media. Part IV. In: J. Membr. Sc. 125 1997, S. 41–59.
Adolf Fick: On liquid diffusion. Philos. Mag., 10:30, 1855.
A. Mauro: Nature of solvent transfer in osmosis. In: Science. 126, 1957, S. 252.
Christoph Steinert. Thermoosmose in Flüssigkeiten. Dissertation an der Technischen Hochschule Aachen, 1958.
W. Grosse, H. B. Bücher, H. Tiebel: Pressurized ventilation in wetland plants. In: Acquatic Botany. 39, 1991, S. 89–98.
G. Czihak, H. Langer, H. Ziegler: Biologie, Ein Lehrbuch. 2. Auflage. Springer-Verlag, Berlin 1978, ISBN 3-540-08273-5.
Stefanie Brookmann: Osmolyte und Osmolystrategien von humanen und murinen hämotopoetischen Stamm- und Progenitorzellen. Inauguraldissertation 2007, DNB 987347217.
Gerd Wedler: Lehrbuch der physikalischen Chemie. 4., völlig überarb. und erw. Auflage. Weinheim 1997, ISBN 978-3-527-29481-7.
F. Kiil: Kinetic model of osmosis through semipermeable and solute-permeable membranes. 2002. doi:10.1046/j.1365-201X.2003.01062.x
Hans Keune: „chimica, Ein Wissensspeicher“, Band II, VEB Deutscher Verlag für Grundstoffindustrie Leipzig, 1972, Osmotischer Koeffizient, S. 146, Gl.8.49.
Hans Keune: „chimica, Ein Wissensspeicher“, Band II, VEB Deutscher Verlag für Grundstoffindustrie Leipzig, 1972, Osmotischer Koeffizient, S. 146, Gl.8.50.
Hans Keune: „chimica, Ein Wissensspeicher“, Band II, VEB Deutscher Verlag für Grundstoffindustrie Leipzig, 1972, Osmotischer Koeffizient, S. 147, Gl.8.55.
Hans Keune: „chimica, Ein Wissensspeicher“, Band II, VEB Deutscher Verlag für Grundstoffindustrie Leipzig, 1972, Ionenstärke und osmotischer Koeffizient, S. 146, Gl.8.46.
Video: Traubesche Zelle, Institut für den Wissenschaftlichen Film (Hrsg.), 1982, doi:10.3203/IWF/C-1454
H. Sehon: Physikalische Chemie. Verlag Herder, Freiburg. i. Brsg. 1976, ISBN 3-451-16411-6.
Wasserpotential. In: P. Sitte, E. W. Weiler, J. W. Kadereit, A. Bresinsky, C. Körner: Strasburger – Lehrbuch der Botanik. Spektrum Gustav Fischer, 2002, ISBN 3-8274-1010-X.
spektrum.de Spektrum-Verlag: Kompaktlexikon der Biologie: Kohäsionstheorie der Wasserleitung, abgerufen am 27. Sep. 2019
jstor.org U. Zimmermann, A. Haase, D. Langbein, F. Meinzer: Mechanisms of Long-Distance Water Transport in Plants: A Re-Examination of Some Paradigms in the Light of New Evidence, in Philosophical Transactions: Biological Sciences vol. 341, No. 1295, The Transpiration Stream (29. Jul. 1993), Seiten 19–31, abgerufen am 27. Sep. 2019
H. Plattner, J. Hentschel: Zellbiologie. 3. Auflage. Georg Thieme Verlag, Stuttgart 2007, ISBN 978-3-13-106513-1, S. 361.
Lehninger, Nelson, Cox: Lehninger Biochemie. 3. Auflage. Springer-Lehrbuch, Berlin 2001, ISBN 3-540-41813-X.
Osmotic Power. (Nicht mehr online verfügbar.) Statkraft, Norwegen, archiviert vom Original am 10. November 2013; abgerufen am 27. November 2015 (englisch).
Salz in unserem Tank: Süßwasser plus Salzwasser gleich Strom. (Memento vom 24. Januar 2008 im Internet Archive) In: Financial Times Deutschland. 23. Jan. 2008.
Crown Princess of Norway to open the world’s first osmotic power plant. In: Pressemitteilung. Statkraft, Norwegen, 7. Oktober 2009, abgerufen am 27. November 2015 (englisch).
Statkraft halts osmotic power investments. Statkraft, Norwegen, 20. Dezember 2013, abgerufen am 27. November 2015 (englisch).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Siehe z. B. U. Krey, A. Owen: Basic Theoretical Physics – A Concise Introduction. Springer, Berlin 2007, ISBN 978-3-540-36804-5 (relevant für die Statistische Physik und insbesondere für physikalisch-chemische Aspekte ist besonders Teil 4).

[KedemKatchalsky-2] O. Kedem, A. Katchalsky: Thermodynamic analysis of the permeability of biological membranes to non-electrolytes. In: Biochim. Biophys. Acta. 27 (1958), S. 229–246. doi:10.1016/0006-3002(58)90330-5

[BORG2003-3] Frank G. Borg: arxiv:physics/0305011v1 What is Osmosis. arXiv.org, e-Print 2003.

[GUELL96-4] David C. Guell, Howard Brenner: Physical Mechanism of Membrane Osmotic Phenomena. 1996 doi:10.1021/ie950787f

[MOLUNDERSTAND-5] A. V. Raghunathan, N. R. Aluru: Molecular Understanding of Osmosis in Semipermeable Membranes. In: Physical Review Letters. Band 97, Nr. 2. American Physical Society, 10. Juli 2006, ISSN 1079-7114, S. 024501-(1–4), doi:10.1103/PhysRevLett.97.024501.

[6] L’Abbé Nollet (Juni 1748): Recherches sur les causes du bouillonnement des liquides. In: Mémoires de Mathématique et de Physique, tirés des registres de l’Académie Royale des Sciences de l’année 1748, S. 57–104

[HWSMITH1960-7] Homer W. Smith, Homer W. Smith: I. Theory of Solutions: A knowledge of the laws of solutions … In: Circulation. Band 21, Nr. 5, Mai 1960, S. 808–817, S. 810, doi:10.1161/01.CIR.21.5.808.

[Dutrochet1826-8] Henri Dutrochet: L’Agent Immédiat du Movement Vital Dévoilé dans sa Nature et dans son Mode d’Action chez les Végétaux et chez les Animaux (Paris: Dentu, 1826), S. 115 und 126.

[Dutrochet1828-9] Henri Dutrochet: Nouvelles Recherches sur l’Endosmose et l’Exosmose, suivies de l’application expérimentales de ces actions physiques à la solution du problême de l’irritabilité végétale. Paris, 1828 (eingeschränkte Vorschau in der Google-Buchsuche).

[OSMOUNT1877-10] Wilhelm Pfeffer: Osmotische Untersuchungen – Studien zur Zellmechanik. Engelmann, Leipzig 1877; archive.org.

[MorseAllPages-11] Harmon Northrop Morse: The Osmotic Pressure of Aqueous Solutions: Report on Investigations Made in the Chemical Laboratory of the Johns Hopkins University During the Years 1899–1913. Carnegie institution of Washington, 1914, S. 222 (archive.org).

[JCWFRAZER-12] J. C. W. Frazer: The Laws of Dilute Solutions. In: H. S. Taylor (Hrsg.): A Treatise on Physical Chemistry. 2. Auflage. Van Nostrand, New York 1931, S. 353–414.

[13] J. H. van ’t Hoff: The role of osmotic pressure in the analogy between solutions and gases. In: Zeitschrift für physikalische Chemie, 1, 1887, S. 481–508 (englisch); Website Uri Lachish. (PDF; 187 kB)

[HOFF_NOBEL-14] J. H. van ’t Hoff: Osmotical pressure and chemical equilibrium. 1901. Nobel Lecture. (PDF; 40 kB)

[Einstein_Molekularkinetische_Theorie_der_Wärme-15] Albert Einstein: Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. In: Annalen der Physik, 17, 1905; Universität Wien (PDF; 717 kB)

[16] C.E. Reid, B. Breton: Water and Ion Flow Across Cellulosic Membranes. In: Journal. Applied Polymer Sci. 1, 1959, S. 133–143.

[17] S. Loeb, S. Sourirajan: Sea Water Demineralizationby Means of an Osmotic Membrane. In: Adv. Chem. Ser. 38, 1962, S. 117.

[18] Julius Glater: The early history of reverse osmosis membrane development. In: Desalination. Band 117, Nr. 1, 20. September 1998, S. 297–309, doi:10.1016/S0011-9164(98)00122-2.

[19] Wasserpotential. In: P. Sitte, E. W. Weiler, J. W. Kadereit, A. Bresinsky, C. Körner: Strasburger – Lehrbuch der Botanik. Spektrum Gustav Fischer, 2002, ISBN 3-8274-1010-X, S. 254.

[ATKINS2006S166-20] Peter W. Atkins, Julio de Paula: Physikalische Chemie. Wiley-VCH, 2005, ISBN 3-527-31546-2, S. 166.

[KORTÜM-LACHMANN-21] Kortüm, Lachmann: Einführung in die chemische Thermodynamik. Vandenhoeck & Ruprecht, 1981, S. 245, Fußnote 3.

[MEMSEPS75-22] Sun-Tak Hwang, Karl Kammermeyer: Membranes in separation. (Techniques of chemistry, v. VII). John Wiley & Sons, Rochester, NY 1975, ISBN 0-471-93268-X, S. 24.

[VANTHOFFROLE-23] J.H. van ’t Hoff: The role of osmotic pressure in the analogy between solution and gases. In: Zeitschrift fur Physikalische Chemie. 1 (1887), S. 481–508 (englisch); Website Uri Lachish. (PDF; 187 kB)

[STAVERMAN51-24] A.J.Staverman: The theory of measurement of osmotic pressure. In: Rec. Trav. Chim. 70, 1951, S. 344.

[GUELLDISSERT-25] David Charles Guell: The Physical Mechanism of Osmosis and Osmotic Pressure. A Hydrodynamical Theory for Calculating the Osmotic Reflection Coefficient. Massachusetts Institute of Technology, Cambridge 1991, OCLC 24393943 (englisch, hdl:/1721.1/29859 – Doctoral thesis, Dept. of Chemical Engineering.).

[HILL89-26] A. E. Hill: Osmosis in Leakey Pores: The Role of Pressure. In: Proc R. Soc. Lond., B 237, 1989, S. 363–367.

[CHINARDENS74-27] Francis P. Chinard, Theodore Enns: Osmotic pressure. In: Science. 124, 1956, S. 472–474.

[MOORE84-28] Moore, Hummel: Physikalische Chemie. Verlag de Gruyter, 1986, ISBN 3-11-010979-4.

[ATKINS2006S169-29] Peter W. Atkins, Julio de Paula: Physikalische Chemie. Wiley-VCH, 2005, ISBN 3-527-31546-2, S. 169.

[30] R. Ash, R. M. Barrer, A. Vernon, J. Edge, T. Foley: Thermo-osmosis of sorbable gases in porous media. Part IV. In: J. Membr. Sc. 125 1997, S. 41–59.

[FICK1855-31] Adolf Fick: On liquid diffusion. Philos. Mag., 10:30, 1855.

[32] A. Mauro: Nature of solvent transfer in osmosis. In: Science. 126, 1957, S. 252.

[STEINERT58-33] Christoph Steinert. Thermoosmose in Flüssigkeiten. Dissertation an der Technischen Hochschule Aachen, 1958.

[34] W. Grosse, H. B. Bücher, H. Tiebel: Pressurized ventilation in wetland plants. In: Acquatic Botany. 39, 1991, S. 89–98.

[35] G. Czihak, H. Langer, H. Ziegler: Biologie, Ein Lehrbuch. 2. Auflage. Springer-Verlag, Berlin 1978, ISBN 3-540-08273-5.

[BROOKMANN-36] Stefanie Brookmann: Osmolyte und Osmolystrategien von humanen und murinen hämotopoetischen Stamm- und Progenitorzellen. Inauguraldissertation 2007, DNB 987347217.

[37] Gerd Wedler: Lehrbuch der physikalischen Chemie. 4., völlig überarb. und erw. Auflage. Weinheim 1997, ISBN 978-3-527-29481-7.

[KIIL2002-38] F. Kiil: Kinetic model of osmosis through semipermeable and solute-permeable membranes. 2002. doi:10.1046/j.1365-201X.2003.01062.x

[39] Hans Keune: „chimica, Ein Wissensspeicher“, Band II, VEB Deutscher Verlag für Grundstoffindustrie Leipzig, 1972, Osmotischer Koeffizient, S. 146, Gl.8.49.

[40] Hans Keune: „chimica, Ein Wissensspeicher“, Band II, VEB Deutscher Verlag für Grundstoffindustrie Leipzig, 1972, Osmotischer Koeffizient, S. 146, Gl.8.50.

[41] Hans Keune: „chimica, Ein Wissensspeicher“, Band II, VEB Deutscher Verlag für Grundstoffindustrie Leipzig, 1972, Osmotischer Koeffizient, S. 147, Gl.8.55.

[42] Hans Keune: „chimica, Ein Wissensspeicher“, Band II, VEB Deutscher Verlag für Grundstoffindustrie Leipzig, 1972, Ionenstärke und osmotischer Koeffizient, S. 146, Gl.8.46.

[43] Video: Traubesche Zelle, Institut für den Wissenschaftlichen Film (Hrsg.), 1982, doi:10.3203/IWF/C-1454

[44] H. Sehon: Physikalische Chemie. Verlag Herder, Freiburg. i. Brsg. 1976, ISBN 3-451-16411-6.

[45] Wasserpotential. In: P. Sitte, E. W. Weiler, J. W. Kadereit, A. Bresinsky, C. Körner: Strasburger – Lehrbuch der Botanik. Spektrum Gustav Fischer, 2002, ISBN 3-8274-1010-X.

[46] spektrum.de Spektrum-Verlag: Kompaktlexikon der Biologie: Kohäsionstheorie der Wasserleitung, abgerufen am 27. Sep. 2019

[47] stor.org U. Zimmermann, A. Haase, D. Langbein, F. Meinzer: Mechanisms of Long-Distance Water Transport in Plants: A Re-Examination of Some Paradigms in the Light of New Evidence, in Philosophical Transactions: Biological Sciences vol. 341, No. 1295, The Transpiration Stream (29. Jul. 1993), Seiten 19–31, abgerufen am 27. Sep. 2019

[Zellbiologie_361-48] H. Plattner, J. Hentschel: Zellbiologie. 3. Auflage. Georg Thieme Verlag, Stuttgart 2007, ISBN 978-3-13-106513-1, S. 361.

[LEHNINGERD3-49] Lehninger, Nelson, Cox: Lehninger Biochemie. 3. Auflage. Springer-Lehrbuch, Berlin 2001, ISBN 3-540-41813-X.

[50] Osmotic Power. (Nicht mehr online verfügbar.) Statkraft, Norwegen, archiviert vom Original am 10. November 2013; abgerufen am 27. November 2015 (englisch).

[51] Salz in unserem Tank: Süßwasser plus Salzwasser gleich Strom. (Memento vom 24. Januar 2008 im Internet Archive) In: Financial Times Deutschland. 23. Jan. 2008.

[52] Crown Princess of Norway to open the world’s first osmotic power plant. In: Pressemitteilung. Statkraft, Norwegen, 7. Oktober 2009, abgerufen am 27. November 2015 (englisch).

[53] Statkraft halts osmotic power investments. Statkraft, Norwegen, 20. Dezember 2013, abgerufen am 27. November 2015 (englisch).