Hydrostatischer Druck

Der hydrostatische Druck (altgriechisch ὕδωρ hýdor, deutsch ‚Wasser‘) ist der Druck innerhalb eines ruhenden Fluids, wobei es sich um eine Flüssigkeit, ein Gas oder ein Plasma handeln kann. Der hydrostatische Druck kann beispielsweise von den das Fluid umschließenden Wänden erzeugt werden (siehe Zylinder mit Kolben), oder Resultat der Schwerebeschleunigung (Gravitationsdruck oder Schweredruck) oder Trägheit sein (z B. in einer Zentrifuge). Häufig wird der hydrostatische Druck von außen vom Umgebungsdruck oder dem Betriebsdruck aufgebracht,[1] unter dem das Fluid ruht. Nach dem Pascalschen Prinzip (von Blaise Pascal) breitet sich der hydrostatische Druck im Fluid allseitig aus und wirkt nach Euler[2] im Volumen in alle Richtungen, auf Wände aber immer senkrecht.

Ohne äußeres Kraftfeld ist der hydrostatische Druck im Fluid überall gleich, insbesondere die Form eines Behälters, in dem das Fluid ruht, hat keinerlei Einfluss, solange Kapillarität vernachlässigbar ist (wie z. B. in ausreichend großen kommunizierenden Röhren). Der im Fluid herrschende hydrostatische Druck wirkt auf alle Flächen, die das Fluid begrenzen, mit einer senkrecht auf das jeweilige Flächenstück gerichteten flächenverteilten Kraft.

Der statische Druck ist das Gegenstück zum hydrostatischen Druck in bewegten Fluiden. Nach dem Bernoulli-Effekt ist der Druck in strömenden Teilen eines Strömungsfelds geringer als in Regionen mit ruhendem Fluid (auf gleicher Höhe des äußeren Kraftfelds, falls vorhanden.)[3]^:64; die Druckdifferenz führt den Namen Staudruck oder dynamischer Druck und wird demnach durch Fluidströmungen verursacht.

Der (hydro)statische Druck ist der Druck, den ein Fluidelement im Fluidkörper spürt. Im Gleichgewichtszustand entspricht er dem thermodynamischen Druck, der über eine Zustandsgleichung mit der Dichte, Temperatur und anderen physikalischen Größen zusammenhängt.

Inkompressible Flüssigkeiten im homogenen Schwerefeld

Pascalsches Gesetz

Der hydrostatische Druck am Boden ist trotz unterschiedlicher Füllmengen in allen drei Gefäßen gleich groß.

Der hydrostatische Druck für ein Fluid mit konstanter Dichte im homogenen Schwerefeld berechnet sich nach dem Pascalschen Gesetz (benannt nach Blaise Pascal):

p(h)=\rho gh+p_{0}

Formelzeichen:

\rho

= Dichte [für Wasser:

\rho

≈ 1.000 kg/m³]

g

= Schwerebeschleunigung [für Deutschland:

g

≈ 9,81 m/s²]

h

= Höhe des Flüssigkeitsspiegels über dem betrachteten Punkt

p_{0}

= Druck an der Flüssigkeitsoberfläche (z. B. Luftdruck)

p(h)

= hydrostatischer Druck in Abhängigkeit von der Höhe des Flüssigkeitsspiegels.[4]

Bei der Ermittlung des Drucks auf die Behälterwand spielt der Umgebungsdruck (auch Betriebsdruck genannt[1]) keine Rolle, da er als additive Konstante im Druck überall gleich wirkt, und da der Luftdruck $p_{0}$ gleichermaßen von oben (über die Wasseroberfläche) und von unten einwirkt kann er vernachlässigt werden. Der durch das Fluid ausgeübte Druck auf den Boden eines wassergefüllten Gefäßes ist durch den Druck $\rho gh$ der Wassersäule gegeben. Solange Kapillarität gering ist, hängt der Bodendruck nicht von der Form oder Größe des Gefäßes ab, sondern nur von der Füllhöhe $h$ , während die auf den Boden wirkende Kraft proportional zur Bodenfläche zunimmt. Dies ist das Prinzip der Kraftverstärkung in der hydraulischen Presse, das erstmals Blaise Pascal 1653 formulierte.[5]

Druckverteilung in einer Flüssigkeit ohne Schwerkraft

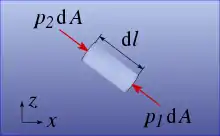
Zyliner (hervorgehoben) mit Länge dl und Stirnfläche dA in einem Fluid (bläulich)

Jede Flüssigkeit ist schwer, aber in vielen Fällen, insbesondere unter hohen Umgebungsdrücken, kann der Einfluss der Schwerkraft vernachlässigt werden; einen solchen Fall zeigt die Abbildung rechts. Der hervorgehobene Zylinder ist im umgebenden Druckfeld in Ruhe.

Die Druckkräfte auf der Mantelfläche des Zylinders wirken senkrecht zur Mantelfläche und damit auch senkrecht zur Zylinderachse. Die Kräfte tragen deshalb nicht zu den Kraftkomponenten parallel zur Zylinderachse bei, und das unabhängig davon, wie der Druck auf der Mantelfläche verteilt ist.
Der Druck auf den Stirnflächen kann bei kleinen Inhalten dA als gleichverteilt angenommen werden. Dann ist die Druckkraft am einen Ende p₁ dA und am anderen Ende p₂ dA und ersterer entgegen gesetzt. Der Zylinder bleibt genau dann in Ruhe, wenn sich die Druckkräfte gegenseitig aufheben, also

p₁ dA = p₂ dA → p₁ = p₂

ist. Die Lage und Orientierung des Zylinders ist dabei offenbar ohne Belang.

Innerhalb des Fluids ist in Abwesenheit einer Schwerkraft (und anderer äußerer Kräfte) der Druck in allen Richtungen und an allen Orten im Fluid gleich groß.

Druckverteilung in einer Flüssigkeit mit Schwerkraft

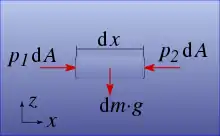
Zyliner (hervorgehoben) mit Länge dx und Stirnfläche dA in einem Fluid (bläulich)

Ähnliche Verhältnisse wie bei der #Druckverteilung in einer Flüssigkeit ohne Schwerkraft liegen bei einer lotrecht wirkenden Schwerkraft und einem horizontal orientierten Zylinder vor, siehe Bild.

Genauso wie die Druckkräfte auf der Mantelfläche, wirkt auch die Gewichtskraft dm·g des Zylinders senkrecht zur Zylinderachse und trägt nichts zu den Kraftkomponenten parallel zur horizontalen Zylinderachse bei.
Der Druck auf den Stirnflächen kann auch hier bei kleinen Inhalten dA als gleichverteilt angenommen werden. Dann ist die Druckkraft am einen Ende p₁ dA und am anderen Ende p₂ dA und ersterer entgegen gesetzt. Der Zylinder bleibt in horizontaler Richtung genau dann in Ruhe, wenn sich wie oben die Druckkräfte auf den Stirnflächen gegenseitig aufheben:

p₁ dA = p₂ dA → p₁ = p₂

Die Orientierung der x-Achse ist dabei offenbar ohne Belang, solange sie nur senkrecht zur Schwerkraft ist. Innerhalb des Fluids ist der Druck in einer horizontalen Ebene und dort in allen Richtungen im Fluid gleich groß.

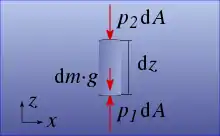
Zyliner (hervorgehoben) mit Länge dz und Stirnfläche dA in einem Fluid (bläulich)

Beim parallel zum Schwerefeld orientierten Zylinder wirkt nun die Gewichtskraft in Richtung der Druckkräfte auf den Stirnflächen.

Die Druckkräfte auf der Mantelfläche wirken horizontal und tragen auch hier nichts zu den Kraftkomponenten parallel zur senkrechten Zylinderachse bei.
In senkrechter Richtung muss die Druckkraft p₁ dA auf der unteren Stirnfläche die Druckkraft p₂ dA auf der oberen Stirnfläche und zusätzlich die Gewichtskraft dm·g des Zylinders tragen, damit der Zylinder seine Höhe beibehält, also weder aufsteigt noch absinkt. Das ist der Fall, wenn

p₁ dA = p₂ dA + dm·g

zutrifft. Der Unterschied der Druckkräfte an den Stellen 1 und 2 ist gleich dem Gewicht der dazwischen liegenden senkrechten Flüssigkeitssäule.

Bei konstanter Querschnittsfläche dA ist das Volumen des Zylinders dA·dz und bei (infinitesimal) kleinem Volumen kann dort die Dichte ρ als konstant angenommen werden mit der Konsequenz dm = ρ·dA·dz:

p₁ dA = p₂ dA + ρg·dA·dz → p₁ = p₂ + ρg·dz

Mit p₁ = p(z) und p₂ = p(z+dz) entsteht nach Division durch dz und Grenzübergang dz → 0 eine autonome Differentialgleichung

{\frac {\partial p}{\partial {\mathsf {z}}}}=-\rho g

die bei konstanter Wichte ρg auf das Pascal’sche Gesetz

p({\mathsf {z}})=p_{0}-\rho g{\mathsf {z}}

führt. Die Integrationskonstante p₀ ist der Druck bei z = 0. Anders als im Abschnitt #Pascalsches Gesetz zählt hier die Koordinate z entgegen der Gewichtskraft nach oben; die Formel dort ergibt sich aus der hiesigen mit h = -z.

Beispiele

Für Taucher ist es wichtig zu wissen, welchem Druck ihre Körpergase (Stickstoff) ausgesetzt sind, um die Taucherkrankheit zu vermeiden.
Ein Bathyscaph muss einem besonders hohen hydrostatischen Druck standhalten.
Wassertürme nutzen den hydrostatischen Druck, um den für die Versorgung der Endverbraucher notwendigen Leitungsdruck zu erzeugen.
In der Hydrogeologie kann sich nach dem Darcy-Gesetz eine Strömung zwischen zwei Punkten nur dann einstellen, wenn die Druckdifferenz verschieden von der Differenz der hydrostatischen Drücke an den beiden Punkten ist.
Ein Heber ist ein Gerät oder eine Einrichtung, mit der man eine Flüssigkeit aus einem Behälter über den Behälterrand in einen tiefer gelegenen Behälter umfüllen oder ins Freie entleeren kann, ohne den Behälter umzukippen und ohne dass er ein Loch oder einen Auslass unter dem Flüssigkeitsspiegel hat.

Gravitationsdruck in Planeten, Monden, Asteroiden und Meteoriten

Tiefenabhängigkeit von g

Mit zunehmender Tiefe kann die Schwerebeschleunigung $g$ nicht mehr als konstant betrachtet werden. Wenn die Form des Himmelskörpers durch eine Kugel mit Radius $R$ beschrieben und die Dichte als konstant betrachtet wird, lässt sich der Druck wie folgt berechnen:

p(h)=\int _{0}^{h}\rho \,g(R-r)\,\mathrm {d} r

.

Der Ortsfaktor $g(r)$ folgt aus dem Newtonschen Gravitationsgesetz:

g(r)=G{\frac {M(r)}{r^{2}}}=G{\frac {Mr}{R^{3}}}=\rho r{\frac {4\pi G}{3}}

,

wobei $M(r)$ die Masse innerhalb einer konzentrischen Kugel innerhalb des Himmelskörpers und $M=M(R)$ dessen Gesamtmasse angibt. Mit der Formel für das Kugelvolumen $V={\tfrac {4}{3}}\pi R^{3}$ ergibt sich für den Druck im Zentrum:

p_{\text{Z}}=p(R)={\frac {3G}{8\pi }}{\frac {M^{2}}{R^{4}}}=\rho ^{2}R^{2}{\frac {2\pi G}{3}}

.

Gravitationsdruck in Sternen

Sterne im Gleichgewicht

Einen Spezialfall des hydrostatischen Drucks stellt der Gravitationsdruck in Sternen dar. Dieser resultiert aus der den Stern kontrahierenden Schwerkraft. Demgegenüber wirkt z. B. der Strahlungsdruck als den Stern expandierende Kraft. Bei einem stabilen Stern stellt sich dabei ein Gleichgewicht aller Kräfte ein und der Stern hat eine stabile Form. Dies ist näherungsweise der Zustand von Sternen auf der Hauptreihe des Hertzsprung-Russell-Diagramms.

Beispiele für Sterne im Ungleichgewicht

Bei entstehenden Sternen, die sich zusammenziehen, überwiegt der Gravitationsdruck gegenüber der Summe aller Kräfte, die Gegendruck aufbauen. Beispiele für Gegendruck sind der kinetische Gasdruck des Gases selbst und bei anlaufender Fusionsreaktion der Strahlungsdruck durch alle auftretenden Strahlungsarten. Dadurch verändert sich der hydrostatische Druck innerhalb des entstehenden Sterns.

Bei einigen Klassen veränderlicher Sterne treten periodische oder transiente Änderungen der Sterndichte auf, wodurch sich die Materiemenge des Sterns, die innerhalb oder außerhalb einer Sphäre mit einem festen Radius liegt, verändert, und mit ihr auch der hydrostatische Druck bei einem bestimmten Radius vom Sternmittelpunkt aus.

Aufgrund des Sternwindes verlieren Sterne stetig Masse an die Umgebung. Auch dadurch ändert sich der hydrostatische Druck. Bei Hauptreihensternen ist diese Änderung allerdings sehr langsam.

In den Spätstadien des Sternenlebens kommt es ebenfalls zu Veränderungen im Sternaufbau, die sich auf den hydrostatischen Druck im Stern auswirken.

Messung und Einheiten

Die Druckmessung erfolgt mit einem Druckmessgerät.

Die Physikalischen Einheiten für den hydrostatischen Druck sind dieselben, wie für den allgemeinen Druck:

international die SI-Einheit
Pascal (Pa): 1 Pa = 1 N/m²;
zudem in Deutschland und Österreich die „gesetzliche Einheit“
Bar (bar): 1 bar = 100.000 Pa bzw. N/m² (= 100 kPa)

Mehr dazu und Umrechnungen sind in den Hauptartikeln nachzuschlagen.

Einzelnachweise

Betriebsdruck – Lexikon der Physik. Spektrum Verlag, abgerufen am 18. Januar 2022.
István Szabó: Geschichte der mechanischen Prinzipien. Springer, 2013, ISBN 978-3-0348-5301-9 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 1. Mai 2021]).
Ludwig Prandtl: Prandtl-Führer durch die Strömungslehre. Grundlagen und Phänomene. Hrsg.: H. Oertel. 13. Auflage. Springer Vieweg, 2012, ISBN 978-3-8348-1918-5.
Dieter Meschede: Gerthsen Physik. 25. Auflage, Springer Spektrum, Berlin 2015, ISBN 978-3-662-45976-8 (Hardcover), ISBN 978-3-662-45977-5 (eBook).
Blaise Pascal: Abhandlung über das Gleichgewicht von Flüssigkeiten und vom Gewicht der Masse der Luft. Paris 1663 (französisch, archive.org [PDF; abgerufen am 21. April 2017] Originaltitel: Traitez de l'équilibre des liqueurs et de la pesanteur de la masse de l'air. Posthume zweite Veröffentlichung).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Betriebsdruck-1] Betriebsdruck – Lexikon der Physik. Spektrum Verlag, abgerufen am 18. Januar 2022.

[szabo-2] István Szabó: Geschichte der mechanischen Prinzipien. Springer, 2013, ISBN 978-3-0348-5301-9 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 1. Mai 2021]).

[prandtl-3] Ludwig Prandtl: Prandtl-Führer durch die Strömungslehre. Grundlagen und Phänomene. Hrsg.: H. Oertel. 13. Auflage. Springer Vieweg, 2012, ISBN 978-3-8348-1918-5.

[4] Dieter Meschede: Gerthsen Physik. 25. Auflage, Springer Spektrum, Berlin 2015, ISBN 978-3-662-45976-8 (Hardcover), ISBN 978-3-662-45977-5 (eBook).

[5] Blaise Pascal: Abhandlung über das Gleichgewicht von Flüssigkeiten und vom Gewicht der Masse der Luft. Paris 1663 (französisch, archive.org [PDF; abgerufen am 21. April 2017] Originaltitel: Traitez de l'équilibre des liqueurs et de la pesanteur de la masse de l'air. Posthume zweite Veröffentlichung).