Akkretionsscheibe
Eine Akkretionsscheibe ist in der Astrophysik eine um ein zentrales Objekt rotierende Scheibe, die Materie in Richtung des Zentrums transportiert (akkretiert). Sie kann aus atomarem Gas, verschieden stark ionisiertem Gas (Plasma) oder interstellarem Staub bestehen.
.jpg.webp)
Beschreibung
Der Durchmesser von Akkretionsscheiben reicht von einigen hundert Astronomischen Einheiten bis zu hunderten Parsec bei aktiven galaktischen Kernen. Die in den Akkretionsscheiben gespeicherte Materie kann die Masse des akkretierenden Objekts um eine bis zwei Größenordnungen übersteigen. Diese Scheiben werden als selbst-gravitierende Scheiben beschrieben, weil sie von der Gravitationskraft der in ihnen gespeicherten Materie stabilisiert und zusammengehalten werden.
Die Temperatur eines Rings einer Akkretionsscheibe ist eine Funktion der Dichte, der Viskosität und der Rotationsgeschwindigkeit. Sie steigt daher in Richtung des Zentrums an und kann in der Übergangsschicht bis zu einige Millionen Kelvin erreichen.
Das Strahlungsprofil einer Akkretionsscheibe ist in erster Näherung zusammengesetzt aus der Strahlung vieler Ringe unterschiedlicher Temperatur mit unterschiedlichem Abstand vom akkretierenden Objekt und reicht vom Infraroten bis hin zu harter Röntgenstrahlung.
Auftreten
Typische Akkretionsscheiben befinden sich um junge Sterne während und einige Zeit nach der Sternentstehung; hierzu gehören die T-Tauri-Sterne, Herbig-Ae/Be-Sterne und die FU-Orionis-Sterne.
Bei älteren Sternen treten Akkretionsscheiben in Doppelsternsystemen auf, bei denen ein Massefluss von einem Spender zu einem kompakten Objekt stattfindet. Zu diesen Systemen zählen die Sternklassen der Symbiotischen Sterne, der Kataklysmischen Doppelsterne sowie die Röntgendoppelsterne. Die akkretierenden kompakten Objekte sind Neutronensterne, Schwarze Löcher sowie Weiße Zwerge. Seltener handelt es sich um Hauptreihensterne in Algolsternen, Beta-Lyrae-Sternen und Doppelperiodischen Veränderlichen.
Bei den Akkretionsscheiben um die zentralen schwarzen Löcher von Galaxien sind um mehrere Größenordnungen größere Radien und Massentransferraten gefunden worden. Sie manifestieren sich je nach Blickwinkel und Akkretionsrate als Quasare, Aktive galaktische Kerne oder Seyfertgalaxien.
In Akkretionsscheiben um Neutronensterne und Schwarze Löcher wird potentielle Gravitationsenergie umgesetzt, sodass die differentiell rotierenden Scheiben durch die Viskosität hell aufleuchten. Dieser Mechanismus kann je nach Kompaktheit, dem Quotient aus Masse und Radius des Objektes, bis zu 20-mal so effektiv sein wie die Erzeugung von Strahlung durch nukleare Prozesse, z. B. durch die Kernfusion. Außerdem bildet sich oft aus der verschlungenen Materie ein sogenannter Jet.
Formen von Akkretionsflüssen
Advektionsdominierter Akkretionsfluss (ADAF)

ADAF steht für advection-dominated accretion flow[1], darunter versteht man eine aufgeblähte Materieströmung aus heißem, dünnem Gas, die eine etwa kugelige Gestalt um das Materie aufsammelnde Zentralobjekt annimmt. Die Astronomie ist auf die Existenz dieser heißen Akkretionsflüsse um kosmische Objekte wie Neutronensterne oder Schwarzer Löcher angewiesen, um erklären zu können, wie hochenergetische Röntgenspektren zustande kommen.
Eigenschaften
Ein ADAF ist eine spezielle, analytische Lösung, die in der Akkretionsphysik sehr bekannt ist. Der ADAF wurde 1994 entdeckt[2] und weist ein paar klare Unterschiede zur Standardscheibe (SSD), auf. Im Wesentlichen liegt das darin begründet, dass die akkretierte Materie nicht effizient durch Strahlung gekühlt wird. Das ist eine so markante Eigenschaft, dass sich für solche Akkretionsflüsse der Oberbegriff RIAF für radiatively-inefficient accretion flow (durch Strahlung ineffizient gekühlter Akkretionsfluss) etabliert hat[3]. Jeder ADAF ist demnach ein RIAF – aber nicht umgekehrt. Das Unterbleiben der Kühlung führt zur Aufheizung des Akkretionsflusses, der sich dadurch ausdehnt und ausgedünnt wird. Ein solch dünnes Gas kann durch Strahlung schlecht gekühlt werden, weil es kaum Wechselwirkungen zwischen Gas und Strahlung gibt. Im Gegensatz zur Standardscheibe wird die thermische Energie nicht durch elektromagnetische Wellen abgestrahlt, sondern im Gas als innere Energie und Entropie gespeichert. Der radiale Entropiegradient ist eine geeignete Größe, um den Unterschied der beiden wichtigsten analytischen Akkretionslösungen zu beschreiben. Der Entropiegradient verschwindet bei SSDs aber nicht bei ADAFs. Die somit im ADAF gespeicherte Energie wird durch das aufsammelnde Objekt, den sogenannten Akkretor, geschluckt.
Teilchenbewegungen
Das Geschwindigkeitsfeld im ADAF ist sub-Keplersch, d. h., dass bei einem vorgegebenen Radius die Rotation nur etwa 40 % der Keplerschen Umlaufgeschwindigkeit an diesem Radius ist. Die radiale Geschwindigkeit, also die Einfallgeschwindigkeit in Richtung auf das Zentralobjekt, ist vergleichbar mit dieser sub-Keplerschen Rotationsgeschwindigkeit. ADAFs bilden sich typischerweise bei kleinen Akkretionsraten aus. Pro Zeiteinheit fällt verhältnismäßig wenig Materie auf den Akkretor. Bei hohen Akkretionsraten dominieren andere Akkretionslösungen, wie die Standardscheibe oder die sogenannten schlanken Scheiben (slim disks)[4].
Standardscheibe (SSD)

Die Standardscheibe als Akkretionslösung wurde 1973 von Nikolai Shakura und Rashid Sunyaev entdeckt. Daher wird die Standardakkretionsscheibe (standard accretion disk, kurz: SAD) auch Shakura-Sunyaev-Disk oder SSD genannt.[5] Kurze Zeit später wurde die SSD-Lösung relativistisch verallgemeinert[6]. Die Standardscheibe ist einer von vielen Akkretionsflüssen, die auf der reinen Hydromechanik ohne Magnetfelder basiert und bezeichnet eine Materieströmung, die um ein zentrales, kosmisches Objekt rotiert. Der Materiefluss sammelt sich in einer flachen Scheibe, der sogenannten Akkretionsscheibe. Im Gegensatz zum ADAF findet man die Standardscheibe in unterschiedlicher Ausprägung in allen Akkretionsflüssen – unabhängig von der Akkretionsrate. Diese Aussage deutet sich zumindest in einem vereinheitlichenden Akkretionsmodell (accretion unification scheme) an[7].
Eigenschaften
Die Strömung rotiert in einer flachen, geometrisch dünnen Materiescheibe. Das Verhältnis von Scheibenhöhe H und typischen Scheibenradius R nennt man Skalenhöhe, diese ist für Standardscheiben viel kleiner als 1. Rotierende Materie besitzt Drehimpuls. Der Akkretionsfluss muss zu einer Scheibe abflachen, weil dieser Zustand energetisch günstiger ist und von der Drehimpulserhaltung diktiert wird. Die Scheibenform bzw. Achsensymmetrie ist gerade die korrespondierende Symmetrieeigenschaft zum erhaltenen Drehimpuls.
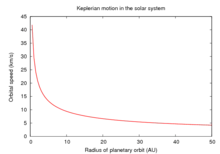
Gas- und Staubscheiben rotieren generell nicht als starrer Körper, sondern differentiell. Man kann anhand von spektralen Rot- und Blauverschiebungen die Orbitalgeschwindigkeit in Abhängigkeit vom Radius messen. Akkretionsscheiben um Sterne oder Mehrfachsternsysteme, bei denen die Orbitalgeschwindigkeit gemäß dem 3. Keplerschen Gesetz vom Radius abhängt (),[8] werden auch als Keplerscheiben bezeichnet. Für diese gilt, dass die Scheibe selbst so wenig Masse enthält, dass ihre Rotation praktisch nur vom Zentralstern bzw. den Zentralsternen bestimmt wird.
Die Umlaufgeschwindigkeit nimmt mit der Annäherung an das Zentralobjekt zu. Es gibt allerdings einen innersten Rand der Scheibe, denn stabile Rotation bricht an der marginal stabilen Bahn zusammen. Dieser Innenrand heißt auch innerste stabile Kreisbahn (innermost stable circular orbit, ISCO)[9]. Die langsame Einfallbewegung zum Zentralobjekt nennt man „radial Drift“.
Das Scheibenmaterial bewegt sich mikroskopisch wie eine zähe Flüssigkeit turbulent – also ungeordnet. Das Keplersche Geschwindigkeitsprofil ist demgegenüber eine geordnete, makroskopische Bewegung. Sie bedingt, dass benachbarte Ringe von Scheibenmaterial unterschiedlich schnell rotieren. Diese Flüssigkeitsringe stehen miteinander in Verbindung, so wie die Teilchen in einer Flüssigkeit locker zusammen gehalten werden. Doch die Rotation verschiebt die Ringe gegeneinander. Bei dieser Scherung wird dem Scheibenmaterial turbulente Bewegungsenergie entzogen und in Wärmeenergie umgewandelt.
Generell heißt die Umwandlung einer Energie in Wärmeenergie Dissipation. Die Dissipation in Standardscheiben ist eine Folge der turbulenten, hydrodynamischen Viskosität. Der Temperaturverlauf in der Standardscheibe ist auf der Grundlage des Modells nach Shakura & Sunyaev genau bekannt. Die Scheibentemperatur T folgt einem Potenzgesetz und nimmt nach innen mit dem Radius r zu, aber sie nimmt mit der Masse M des Zentralobjekts ab. Die Maximaltemperatur am Innenrand hängt generell von der Masse des Zentralobjekts, der Akkretionsrate und dem Ort des Innenrands (ISCO) ab. Eine typische Maximaltemperatur in der Nähe eines supermassereichen Schwarzen Loches von 100 Millionen Sonnenmassen ist etwa eine Million Kelvin. Das entspricht etwa einem Zehntel der Zentraltemperatur der Sonne. Diese hohen Temperaturen belegen, dass das Scheibenmaterial häufig ein Plasma ist. Atomare und molekulare Standardscheiben sind nur bei tieferen Temperaturen denkbar. Dennoch spricht man oft von kalten Standardscheiben. Diese Bezeichnungsweise hat sich ergeben, weil es einen noch deutlich heißeren Akkretionsfluss gibt, den ADAF. Die Strahlung der Standardscheibe ist thermisch. Man kann sich die dünne Scheibe in Ringe zerlegt denken, von denen jeder Ring eine bestimmte Temperatur hat. Jeder Ring kann wie ein Planckscher Wärmestrahler behandelt werden, der bei einer bestimmten Wellenlänge sein Strahlungsmaximum annimmt. Das gesamte Spektrum der Standardscheibe ist entsprechend die Summe aller Ringe.
Die optische Leuchtkraft der Standardscheibe ist proportional zur Masse des aufsammelnden Zentralobjekts. Außerdem nimmt die Leuchtkraft auch mit der Akkretionsrate zu. Durch die Abstrahlung elektromagnetischer Wärmestrahlung verliert der Akkretionsfluss Energie. Die Kühlung ist bei Standardscheiben besonders effizient. Das heißt, die thermische Energie des Materiestroms wird nahezu vollständig als Strahlungsenergie abgestrahlt. Das sorgt zusammen mit der Rotation dafür, dass der Akkretionsfluss in sich zusammenfällt und Standardscheiben dünne, abgeflachte Akkretionsflüsse sind. Dadurch wird das Scheibenmaterial verdichtet. Innerhalb der Scheibe kann sich elektromagnetische Strahlung kaum fortpflanzen, weil sie durch den Strahlungstransport ständig gestreut, absorbiert, reemittiert und reabsorbiert wird. Standardscheiben sind daher mehr oder weniger undurchsichtig (opak) für elektromagnetische Wellen. Diese Eigenschaft der Undurchsichtigkeit bei Standardscheiben verlieh ihnen das Attribut optisch dick.
Teilchenbewegungen
Zusammenfassend kann man sagen, dass in Akkretionsflüssen wie den Standardscheiben Energieformen ineinander umgewandelt werden. Am Anfang steht die Gravitationsenergie, eine potentielle Energie, die Materie in einigem Abstand zum Akkretor hat. Diese Energie der Lage wird im Falle der Standardscheiben zunächst vor allem in Rotationsenergie umgewandelt. Scherung und Turbulenz bewerkstelligen eine Umwandlung in thermische Energie. Schließlich findet eine Umwandlung in Strahlungsenergie statt. Dieser letzte Umwandlungsprozess ist der entscheidende für die Astronomie, machen sich doch auf diese Weise die kosmischen Objekte aus großer Entfernung bemerkbar.
Weitere Akkretionsflüsse
Das NRAF-Modell (non-radiative accretion flow) ist seit 1999 etabliert und wird aktuell intensiv weiterverfolgt. Prinzipiell subsumiert das Akronym NRAF sämtliche Akkretionsflüsse, die nicht durch Strahlung gekühlt oder geheizt werden können. Der heiße Akkretionsfluss kann innen, nahe vor dem gravitierenden Objekt, einen advektiven Torus ausbilden.
Die ersten NRAF-Modelle waren rein hydrodynamisch.[10] Später wurden die Modelle durch die Berücksichtigung von Magnetfeldern verfeinert.[11] Dann ist eine wesentliche Zutat im Modell die ideale Magnetohydrodynamik. Dahinter verbirgt sich die einfachste Form der MHD, die nicht dissipativ ist. Viskositäten und Wärmeleitung werden nicht berücksichtigt. Das hat den numerischen Vorteil, dass das Gleichungssystem deutlich einfacher ist. Doch bereits die ideale MHD zeigt einen wichtigen Mechanismus: die bereits angedeutete Magnetorotationsinstabilität oder magnetische Rotationsinstabilität (engl. magneto-rotational instability, MRI). Diese Instabilität wurde von Balbus und Hawley 1991 entdeckt.[12] Das führte zum alternativen Namen Balbus-Hawley-Instabilität. Die MRI ist wesentlich, um zu verstehen, weshalb Materie einer Akkretionsscheibe – trotz des hohen Drehimpulses – in ein Schwarzes Loch fallen kann. Die MRI sorgt für einen sehr effizienten Drehimpulstransport. Die damit verbundene magnetische Turbulenz ist deutlich wichtiger als die hydrodynamische Turbulenz. Damit diese MHD-Instabilität funktionieren kann, benötigt man nur ein rotierendes Objekt, z. B. einen Torus oder eine schlanke Akkretionsscheibe, und ein schwaches Magnetfeld, das dieses Objekt durchsetzt.
Eine Alternative zum SSD-ADAF-Szenario heißt TDAT das für (truncated disk – advective tori), also trunkierte Scheiben – advektive Tori, steht. Das TDAT-Modell (Hujeirat & Camenzind 2000) ist dadurch charakterisiert, dass eine flache Akkretionsscheibe bereits bei deutlich größeren Radien als der marginal stabilen Bahn endet[13]. Weiter innen schließt sich ein heißer ADAF an. Es wurden viele advektionsdominierte Modelle in den letzten Jahren vorgeschlagen. So kennt man Modelle wie die ADIOS (advection-dominated inflow/outflow solutions), bei dem auch signifikante Ausflüsse (Winde) berücksichtigt werden. Beim CDAF (convection-dominated accretion flow) spielt die Konvektion des akkretierten Plasmas eine wichtige Rolle.
Mechanismus der Akkretion
Aus der differentiellen Rotation um das Zentralobjekt (die inneren Bereiche rotieren aufgrund der Keplerschen Gesetze schneller) ergeben sich Reibungs- und Scherkräfte. Durch solche und andere turbulente Prozesse in der Scheibe werden Teilchen in Richtung des Zentralobjekts befördert, so dass dieses Masse gewinnt (akkretiert). Dazu müssen die Teilchen ihren Drehimpuls nach außen abführen (Drehimpulserhaltung), indem sie ihn auf andere Teilchen übertragen, die als Folge vom Zentralobjekt „weggedrückt“ werden.
Die molekulare Viskosität ist zu klein, um für den Drehimpulsübertrag in der nötigen Größenordnung verantwortlich zu sein. Deshalb nimmt man an, dass die Scheibe turbulent wird und dies eine Viskosität erzeugt. Bei schwach ionisierten Scheiben übernehmen die Magnetfelder, die die Ionen unvermeidlich mit sich tragen, eine wichtige Rolle: sie bewirken Instabilität (Magnetorotationsinstabilität (MRI)), die zu Turbulenz in der Scheibe und damit zu einer dynamischen Viskosität führen. Die Theorie zur Beschreibung von Plasmen in Magnetfeldern ist die Magnetohydrodynamik (MHD).
Disc Instability Model
Akkretionsscheiben pendeln bei einer Reihe von Sternklassen zwischen zwei Zuständen, was auch als Disc Instability Model (dt. Scheibeninstabilitätsmodell) bezeichnet wird:
- ein Zustand mit hoher Viskosität (d. h. hoher innerer Reibung) und hoher Akkretionsrate (d. h. hoher Massentransferrate); in diesem Fall heizt sich die Scheibe aufgrund der hohen Viskosität auf, was zu einem starken Anstieg der elektromagnetischen Strahlung führt.
- ein Zustand mit niedriger Viskosität und niedriger Akkretionsrate.
Die Viskosität des Materials in der Scheibe ändert sich zwischen den beiden Zuständen um einen Faktor 10.
Dieser Zustandswechsel tritt sowohl bei engen Doppelsternen auf (wie z. B. Zwergnovae, AM-Canum-Venaticorum-Sterne und Röntgendoppelsterne geringer Masse) als auch bei Einzelsternen wie den FU-Orionis-Sternen, die in Phasen mit geringen Akkretionsraten als T-Tauri-Sterne klassifiziert werden. Der Zustandswechsel geschieht unabhängig von der chemischen Zusammensetzung; so besteht die Akkretionsscheibe bei den AM-CVn-Sternen fast ausschließlich aus Helium und wird in den anderen Fällen meist von Wasserstoff dominiert.
Mit Hilfe des Disc Instability Models lassen sich die Eruptionen in den Sternklassen recht gut beschreiben, bisher ist jedoch für die sprunghafte Änderung der Viskosität keine physikalische Ursache bekannt.[14]
Entstehung
Eine Gaswolke kann sich nur dann unter dem Einfluss der Gravitation zusammenziehen, wenn es in irgendeiner Form Reibung zwischen sich begegnenden Teilchen unterschiedlicher Geschwindigkeit gibt; andernfalls würden die Teilchen auch nach Kollisionen im Mittel die gleiche kinetische Energie behalten und damit auf Dauer nicht weiter unten im Potentialtopf Platz nehmen (d. h. näher zum Zentrum driften). Die Dissipation ist umso größer, je größer die Relativgeschwindigkeiten der Teilchen sind.
Wenn die ganze sich zusammenziehende Wolke einen nennenswerten Gesamt-Drehimpuls hat, erfolgen Begegnungen parallel zur Rotationsachse im Mittel mit höherer Geschwindigkeit als senkrecht zur Achse. Dadurch werden die Bewegungen parallel zur Achse stärker verlangsamt als die, deren Bahndrehimpuls mit dem Gesamtdrehimpuls übereinstimmt (d. h. als die Bewegungen senkrecht zur Achse). Sobald die Bestandteile sich einigermaßen in einer Ebene bewegen, vermindert sich die Relativgeschwindigkeit deutlich und es bleibt eine Scheibe übrig.
Für die Entstehung von Akkretionsscheiben gibt es Modelle. Bei ihnen spielen Strahlungsprozesse für die Dämpfung eine wesentliche Rolle.[15]
Siehe auch
Literatur
- Juhan Frank, Andrew R. King, Derek J. Raine: Accretion power in astrophysics (= Cambridge Astrophysics Series 8). Cambridge University Press, Cambridge u. a. 1985, ISBN 0-521-24530-3.
- Matias Montesinos Armijo: Review: Accretion disk theory. In: Astrophysics. Solar and Stellar Astrophysics. 2012, arxiv:1203.6851v1.
Weblinks
Einzelnachweise
- Advection-Dominated Accretion around Black Holes. In: Cornell University. 12. März 1998, abgerufen am 14. Februar 2019.
- Narayan & Yi, Advection-dominated accretion. In: The Astrophysical Journal. Juni 1994, abgerufen am 8. Februar 2019.
- Radiatively Inefficient Accretion Flow Simulations with Cooling: Implications for Black Hole Transients. In: Cornell University. 4. April 2013, abgerufen am 14. Februar 2019.
- Slim accretion disk model. In: nasa.gov. 2003, abgerufen am 14. Februar 2019.
- Black holes in binary systems. In: harvard.edu. 1973, abgerufen am 14. Februar 2019.
- Novikov & Thorne, Astrophysics of black holes. In: harvard.edu. 1973, abgerufen am 8. Februar 2019.
- Grand Unification of AGN and the Accretion and Spin Paradigms. In: Cornell University. 26. August 1999, abgerufen am 14. Februar 2019.
- COSMOS – The SAO Encyclopedia of Astronomy | COSMOS. In: edu.au. astronomy.swin.edu.au, abgerufen am 28. Mai 2018 (englisch).
- Innermost stable circular orbit of spinning test particle in Kerr-AdS black hole background. In: Cornell University. 15. Dezember 2018, abgerufen am 14. Februar 2019.
- Hydrodynamical non-radiative accretion flows in two dimensions. In: harvard.edu. Dezember 1999, abgerufen am 15. März 2019.
- On the Nature of Angular Momentum Transport in Nonradiative Accretion Flows. In: The Astrophysical Journal. 10. Juli 2002, abgerufen am 15. März 2019.
- A powerful local shear instability in weakly magnetized disks. I – Linear analysis. II – Nonlinear evolution. In: harvard.edu. 20. Juli 1991, abgerufen am 15. März 2019.
- A model for the jet-disk connection in BH accreting systems. (PDF) In: Max-Planck-Institut für Astronomie. 2003, abgerufen am 14. Februar 2019.
- Iwona Kotko, Jean-Pierre Lasota: The viscosity parameter α and the properties of accretion disc outbursts in close binaries. In: Astronomy & Astrophysics. 545, 2012, S. A115, doi:10.1051/0004-6361/201219618, arxiv:1209.0017
- Lexikon der Astrophysik: Akkretion