Ergosphäre

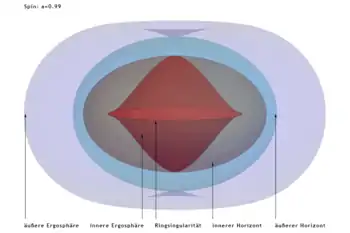
Ergosphäre bezeichnet den in der nebenstehenden Skizze violett eingezeichneten äußersten und den rot eingezeichneten innersten Bereich eines rotierenden Schwarzen Lochs. Ab der äußeren Grenze ist es einem Objekt nicht möglich, nicht zu rotieren; dem Objekt wird damit eine prograde Bewegung aufgezwungen. Ursache für dieses Phänomen ist die Tatsache, dass eine rotierende Masse die Raumzeitgeometrie „mitreißt“, also dass allem, was sich innerhalb der Ergosphäre befindet, die Rotation des Schwarzen Loches aufgezwungen wird. Damit ein Objekt relativ zu einem entfernten Beobachter stationär sein könnte, müsste es lokal mit Überlichtgeschwindigkeit entgegen der Rotationsrichtung der zentralen Masse fliegen, was physikalisch jedoch unmöglich ist. Bis zum Horizont ist es mit einem radialen Impuls jedoch noch möglich, in die Unendlichkeit zu entkommen. Ab der äußeren Grenze der inneren Ergosphäre ist es wieder möglich, sich in jede Richtung zu bewegen, da der Frame-Dragging-Effekt dort wieder unterhalb der Lichtgeschwindigkeit liegt.[2] Größe und Verhalten der Ergosphären werden durch die Kerr-Metrik beschrieben.

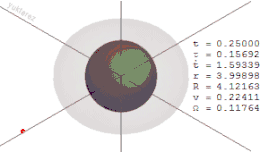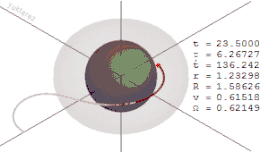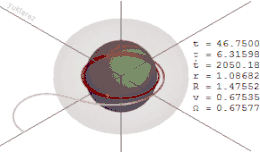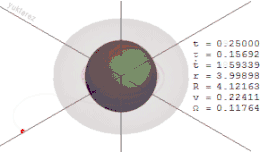
Ein Testpartikel, das sich der Ergosphäre in retrograder Richtung nähert, wird gezwungen, seine Bewegungsrichtung zu ändern. Koordinatensystem: Boyer–Lindquist

Ergosphären und Horizonte eines rotierenden Schwarzen Lochs mit dem Spinparameter a = 0,99.[1]

Das Mitreißen der Raumzeitgeometrie kann man sich bildlich wie die Deformation eines Spinnennetzes vorstellen. Wenn sich das Objekt, das die Raumzeit krümmt, nicht bewegt, ist das Spinnennetz radförmig und die einzelnen „Speichen“ des Rades laufen gerade auf das Objekt zu. Wenn das Objekt aber rotiert, dann „verzwirbelt“ es das Spinnennetz in seinem Zentrum, d. h. die „Speichen“ werden zum Zentrum hin verbogen, und es entsteht ein Bild, das einem Wasserstrudel ähnelt. Aufgrund dieser fortlaufenden Deformation kann sich ein Objekt, auch wenn es sich mit Lichtgeschwindigkeit bewegen würde, nicht mehr der Rotation der Ergosphäre entziehen.

Die räumliche Figur des äußeren Randes der Ergosphäre ist kürbisförmig,[3] während ihr innerer Rand an den äußeren Ereignishorizont in Gestalt eines abgeplatteten Rotationsellipsoids anschließt. Eine hypothetische Extraktion von Rotationsenergie durch den Zerfall eines Teilchens innerhalb der Ergosphäre wird durch den Penrose-Prozess beschrieben.

Literatur

Charles Misner, Kip S. Thorne, John A. Wheeler: Gravitation. W. H. Freeman, San Francisco 1973, ISBN 0-7167-0344-0.
E. F. Taylor, J. A. Wheeler: Exploring black holes: Introduction to General Relativity, Addison-Wesley Longman, San Francisco 2000, ISBN 0-201-38423-X (Project F: The Spinning Black Hole).

Weblinks

Einzelnachweise

Matt Visser: The Kerr spacetime – a brief introduction. (Erstveröffentlichung: arxiv:0706.0622), Seite 35, Fig. 3
Philip Russell Wallace: Physics: Imagination and Reality
Katherine Blundell: Black Holes: A Very Short Introduction S. 31

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Matt Visser: The Kerr spacetime – a brief introduction. (Erstveröffentlichung: arxiv:0706.0622), Seite 35, Fig. 3

[2] Philip Russell Wallace: Physics: Imagination and Reality

[3] Katherine Blundell: Black Holes: A Very Short Introduction S. 31