Singularitäten-Theorem

Als Singularitäten-Theorem bezeichnet man in der allgemeinen Relativitätstheorie der Physik ein Theorem aus der Gruppe von mathematischen Sätzen, die aus wenigen globalen Annahmen über eine Raumzeit das Vorhandensein von Singularitäten in ihr folgern. Die Bedingungen sind einerseits Energiebedingungen an die Masse- und Energieverteilung im Raum und andererseits Kausalitätsbedingungen an die Topologie der Raumzeit.

Solche Theoreme wurden zuerst Ende der 1960er Jahre von Stephen Hawking und Roger Penrose bewiesen[1][2]. Insbesondere für diesen Beitrag erhielt Penrose 2020 den Nobelpreis (Hawking war bereits verstorben), da das Theorem die Existenz Schwarzer Löcher in der Allgemeinen Relativitätstheorie untermauert.

Historische Einordnung

Schon kurz nach der Veröffentlichung der einsteinschen Feldgleichungen 1915 wurde 1916 mit der Schwarzschild-Lösung eine erste exakte Lösung präsentiert. Diese weist als markantes Merkmal starke Symmetrieannahmen auf und es ergibt sich die Möglichkeit für eine Krümmungssingularität im Zentrum. Diese tritt auf, da der unaufhaltsame sphärische Kollaps innerhalb des Ereignishorizontes den Gültigkeitsbereich der Außenraumlösung immer weiter an das Symmetriezentrum annähert. Diese Massenballung schreitet voran, bis theoretisch alle Masse in einem Punkt konzentriert ist und die Krümmung des Raumes an dieser Stelle divergiert. Ein solcher Zusammenbruch der Theorie in so einfachen Modellen kann leicht als ein Artefakt der Symmetrieannahmen eingestuft werden[3]. Mit der Formulierung und dem Beweis der ersten Singularitätentheoreme durch Hawking und Penrose konnte aber gezeigt werden, dass Singularitäten eine Folge der anziehenden Natur der Gravitation sind.

Energiebedingungen

Hauptartikel: Energiebedingungen

In der allgemeinen Relativitätstheorie wird die Massen- und Energieverteilung mit einem Energie-Impuls-Tensor $T_{ab}$ beschrieben. Energiebedingungen sind im Rahmen dieser Theorie Ungleichungen für Kontraktionen dieses Tensors. Die verschiedenen Singularitätentheoreme unterscheiden sich in der Stärke der angewendeten Energiebedingung. Eine starke Bedingung resultiert in einfach zu beweisenden kausalen Singularitäten, aber es gibt eventuell Materieformen im Universum, die dieser widersprechen und nur schwächeren Energiebedingungen gehorchen.

Die schwächsten Energiebedingungen (lichtartige) sind sehr wahrscheinlich von allen Materien erfüllt, daraus folgen allerdings nur lichtartige Singularitäten.

Kausalitätsbedingungen

Kausalität umfasst alle Möglichkeiten, mit denen sich Ereignisse in der Raumzeit beeinflussen können, und ordnet Ereignissen (Raum-Zeit-Koordinaten) Relationen zu. Diese Relationen ergeben sich aus den Tangentialvektoren an den Kurven, die die Ereignisse verbinden. Liegt ein Punkt in der zeitlichen Zukunft eines anderen, so gibt es mindestens eine Verbindungskurve zwischen ihnen mit ausschließlich zeitartigen Tangentialvektoren. Andere Möglichkeiten sind, dass Punkte nur lichtartig in Beziehung stehen oder dass sie nicht kausal verbunden sind (es also nur raumartige Verbindungskurven gibt). Kausal verbunden sind Punkte, wenn es lichtartige oder zeitartige Verbindungskurven gibt. Kausalitätsbedingungen beschränken, in welchen Relationen die gesamten Ereignisse einer Raumzeit zueinander stehen können.

Die Raumzeit ist chronologisch

Die Raumzeit wird als chronologisch bezeichnet, wenn es in ihr keine geschlossenen zeitartigen Kurven gibt. Das bedeutet, dass kein Punkt in seiner eigenen zeitartigen Vergangenheit oder Zukunft liegt.

Die Raumzeit ist kausal

Die Raumzeit wird als kausal bezeichnet, wenn es in ihr keine geschlossenen zeitartigen oder lichtartigen Kurven gibt. Das bedeutet, dass kein Punkt in seiner eigenen kausalen Vergangenheit oder Zukunft liegt.

Die Raumzeit ist streng kausal

Die Raumzeit wird als streng oder stark kausal bezeichnet, wenn keine kausale Kurve eine konvexe Umgebung in zwei unverbundenen Mengen schneidet. Anschaulich gesprochen würde eine Verletzung dieser Bedingung bedeuten, dass man von einem Ereignis über eine kausale Kurve beliebig nahe zurück an dieses Ereignis kommen könnte.

Singularitätentheorem nach Hawking und Penrose

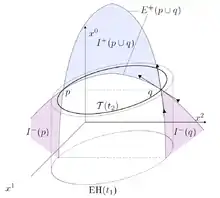
Raumzeitdiagramm, mit Ereignishorizont, einer gefangenen Fläche (Bedingung 4.1. im Theorem) und in einer Ebene x¹=konstant sind der Horismos E⁺ sowie die davon begrenzte Zukunft I⁺ eingezeichnet. Die Kompaktheit des Horismos wird deutlich und dass sowohl die nach außen gerichteten als auch die nach innen gerichteten Nullgeodäten zusammenlaufen (Pfeile in q für den Lichtkegelanteil in der dargestellten Ebene)

Die Raumzeit der Dimension $n$ ist kausalgeodätisch unvollständig, wenn die vier folgenden Punkte erfüllt sind:

Die starke Energiebedingung gilt entlang aller kausaler Kurven (folgt aus der starken Energiebedingung).
Die generische Bedingung ist erfüllt. Das heißt, jede dieser Kurven (mit Tangentialvektorfeld $u^{a}$ ) enthält einen Punkt mit nicht verschwindender effektiver Krümmung: $u^{c}u^{d}u_{[a}R_{b]cd[e}u_{f]}\neq 0$ .
Die Raumzeit ist chronologisch.
Die Raumzeit enthält mindestens eines der folgenden:
1. eine abgeschlossene raumartige Untermannigfaltigkeit ${\mathcal {T}}$ der Dimension $(n-2)$ , deren mittleres Krümmungsvektorfeld vergangenheitsgerichtet und zeitartig ist.
2. eine kompakte achronale (raum- oder lichtartige) Untermannigfaltigkeit ${\mathcal {T}}$ ohne Rand oder
3. einen Punkt $x$ so, dass entlang jeder vollständig in die Vergangenheit (in die Zukunft) fortgesetzten Nullgeodäte vom Punkt $x$ ausgehend mit dem Tangentialvektorfeld $u^{a}$ , die Spur $\theta =u_{\,\,;a}^{a}$ des kovarianten Ableitungstensors $u_{\,\,;b}^{a}$ der Nullgeodätenschar aus $x$ negativ wird.

Ziel dieses Theorems ist es also, die kausalgeodätische Unvollständigkeit der Mannigfaltigkeit zu beweisen. Vereinfacht gesprochen enden also Weltlinien von Beobachtern oder Lichtteilchen einfach an einer Stelle, die nicht mehr zum Raum gehört. Der Beweis basiert darauf, dass Bedingung 1 und 2 zusammen mit angenommener kausalgeodätischer Vollständigkeit einen Widerspruch zu den Bedingungen 3 und 4 bewirken. Wenn 1–4 also zutreffen, muss die kausalgeodätische Vollständigkeit verletzt sein.

Die ersten beiden Bedingungen implizieren eine Fokussierung der kausalen Geodäten. Dies ergibt sich direkt aus der Raychaudhuri-Gleichung und den Existenz- und Eindeutigkeitssätzen über gewöhnliche Differentialgleichungen. Die Fokussierung bewirkt, dass bis zu einer gewissen endlichen Entfernung vom Ursprung der geodätischen Kongruenz mindestens ein Punkt konjugiert zu diesem Ursprung auftreten muss. In einer kausalgeodätisch vollständigen Raumzeit kann man alle Geodäten auf unendliche Parameter fortsetzen. Da die fokussierende Wirkung auf alle kausalen Geodätenscharen wirkt, enthalten dann alle kausalen Geodäten im maximal fortgesetzten Parameterintervall mindestens ein Paar konjugierter Punkte.

Auf der anderen Seite kann man aus den Bedingungen 3 und 4 in einem Bereich, dessen kausale Entwicklung nur durch die Werte auf ${\mathcal {T}}$ vorgegeben ist, eine kausale Kurve konstruieren, die keine konjugierten Punkte aufweist. Aufgrund einer sehr starken Kausalbedingung die in diesem Bereich gilt, der globalen Hyperbolizität, existiert eine kausale Geodäte als Grenzkurve zu dieser konstruierten Kurve. Mit dem Erhalten dieser kausalen Geodäte, die im gesamten Parameterbereich ohne konjugierte Punkte ist, sind die Bedingungen zum Widerspruch geführt und der Beweis erreicht.

Literatur

Stephen Hawking, George F. Ellis: The Large Scale Structure of Space-Time. Cambridge University Press, Cambridge 1973, ISBN 0-521-09906-4 (englisch).
Marcus Kriele: Spacetime. Foundations of general relativity and differential geometry (= Lecture notes in physics. NS M: Monographs. Band 59). Springer, Berlin u. a. 1999, ISBN 3-540-66377-0 (englisch).

Einzelnachweise

Stephen Hawking: The occurrence of singularities in cosmology. T. 1–3. In: Proceedings of the Royal Society. A. Bd. 294, 1966, ISSN 0962-8444, S. 511–521, Bd. 295, 1966, S. 490–493, Bd. 300, 1967, S. 187–201.
Stephen Hawking, Roger Penrose: The singularities of gravitational collapse and cosmology. In: Proceedings of the Royal Society. A. Bd. 314, 1970, ISSN 0962-8444, S. 529–548.
Marcus Kriele: Spacetime, foundations of general relativity and differential geometry. Lecture notes in physics. Bd. 59. Springer, Heidelberg 1999. ISBN 3-540-66377-0, S. 383

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Stephen Hawking: The occurrence of singularities in cosmology. T. 1–3. In: Proceedings of the Royal Society. A. Bd. 294, 1966, ISSN 0962-8444, S. 511–521, Bd. 295, 1966, S. 490–493, Bd. 300, 1967, S. 187–201.

[2] Stephen Hawking, Roger Penrose: The singularities of gravitational collapse and cosmology. In: Proceedings of the Royal Society. A. Bd. 314, 1970, ISSN 0962-8444, S. 529–548.

[3] Marcus Kriele: Spacetime, foundations of general relativity and differential geometry. Lecture notes in physics. Bd. 59. Springer, Heidelberg 1999. ISBN 3-540-66377-0, S. 383