Keplerbahn

Keplerbahnen sind Lösungen des Zweikörperproblems der klassischen Himmelsmechanik, bei dem zwei Massepunkte unter dem Einfluss ihrer gegenseitigen Massenanziehung (Gravitation) sich um den gemeinsamen Schwerpunkt (ihr Baryzentrum) bewegen. Die Formen der Keplerbahnen sind Kegelschnitte: Kreis, Ellipse, Parabel und Hyperbel, wobei sich das Baryzentrum im Brennpunkt der Bahn befindet.

Die vier Formen der Keplerbahnen,
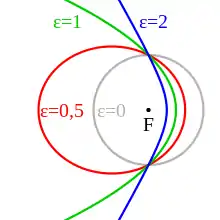
jeweils mit numerischer Exzentrizität: Kreis (grau), Ellipse (rot), Parabel (grün), Hyperbel (blau). Der Brennpunkt ist jeweils der gleiche Punkt F.

Wird das Baryzentrum als stillstehend betrachtet, führen beide Körper synchron eine ähnliche Keplerbahn um das Baryzentrum aus, wobei sie stets entgegengesetzte Punkte zum Baryzentrum einnehmen und das Verhältnis ihrer veränderlichen Abstände zum Baryzentrum stets umgekehrt ihrem Massenverhältnis ist. In der Praxis ist oft ein Körper so viel massereicher als der andere, dass der massereichere Körper auch als stillstehend betrachtet werden kann. Bei dieser Betrachtung führt der masseärmere Körper eine Keplerbahn um den massereicheren Körper aus. Auf annähernden Keplerellipsen bewegen sich z. B. die Planeten, Kometen und Asteroiden um die Sonne, oder der Mond um die Erde.

Für die Orientierung einer Keplerbahn im Raum siehe Bahnelemente. Für die Bewegung auf Keplerbahnen siehe Keplersche Gesetze. Für Abweichungen vom Ideal siehe Bahnstörung.

Details

In Polarkoordinaten zeigt eine Keplerbahn folgende Winkelabhängigkeit des Radius $r$ , also des Abstands des Bahnpunkts vom Schwerpunkt $F$ :[1]

r(\nu )={p \over 1+\varepsilon \cdot \cos \nu }\,.

Darin wird der wahre Anomalie genannte Winkel $\nu$ zwischen Apsidenlinie und Radiusvektor von der Periapsis aus gezählt, die im Bild rechts liegt.

Die numerische Exzentrizität $\varepsilon$ gibt die Streckung der Bahn an:

$\varepsilon =0:$ Kreisbahn
$\varepsilon <1:$ elliptische Bahn
$\varepsilon =1:$ parabolische Bahn
$\varepsilon >1:$ hyperbolische Bahn.

Für die offenen Bahnen (Parabel und Hyperbel) ist der Definitionsbereich von $\nu$ auf das offene Intervall $\pm (\pi -\arccos {\tfrac {1}{\varepsilon }})$ beschränkt. Himmelskörper auf offenen Bahnen haben zum Zentralgestirn einen ungebundenen Zustand. Beispiele sind einige Kometen, die nach einmaliger Näherung an die Sonne ohne Wiederkehr aus dem Sonnensystem verschwinden.

Für verschiedene $\varepsilon$ schneiden sich die Bahnen bei $\nu =\pm {\pi \over 2}$ (der sogenannte Halbparameter $p=r\left(\pm {\pi \over 2}\right)$ skaliert die Form).

Siehe auch

Einzelnachweise

Franz Embacher: Elemente der Theoretischen Physik. Band 1. Springer DE, 2010, ISBN 3-8348-9782-5, S. 134 (eingeschränkte Vorschau in der Google-Buchsuche).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Franz Embacher: Elemente der Theoretischen Physik. Band 1. Springer DE, 2010, ISBN 3-8348-9782-5, S. 134 (eingeschränkte Vorschau in der Google-Buchsuche).