Weißer Zwerg

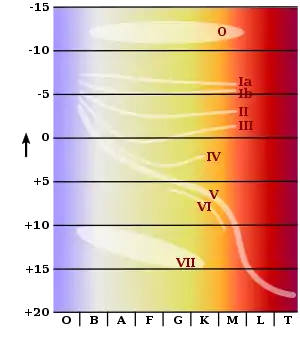
Ein Weißer Zwerg ist ein kleiner, sehr kompakter alter Stern. Er hat trotz seiner hohen Oberflächentemperatur nur eine sehr geringe Leuchtkraft, liegt also im Hertzsprung-Russell-Diagramm weit unterhalb der Hauptreihe. Der hohen Temperatur verdankt er seine weiße Farbe, der geringen Leuchtkraft – die auf eine entsprechend kleine Sternoberfläche hinweist – die Bezeichnung „Zwerg“. Während Hauptreihensterne wie die Sonne Radien in der Größenordnung von 10⁶ km haben, beträgt der Radius eines Weißen Zwerges mit 7000 bis 14.000 km nur 1 bis 2 Erdradien. Dennoch haben Weiße Zwerge die Masse eines Sterns. Sie bestehen im Normalfall aus einem Kern aus heißer entarteter Materie von extrem hoher Dichte, umgeben von einer dünnen, leuchtenden Photosphäre.

Hertzsprung-Russell-Diagramm

Spektralklasse

Absolute
Hellig-
keit
(mag)

Weiße Zwerge sind nach dem Ende jeglicher Kernfusion das Endstadium der Entwicklung der meisten Sterne, deren nuklearer Energievorrat versiegt ist. Sie sind die heißen Kerne Roter Riesen, die übrig bleiben, wenn jene ihre äußere Hülle abstoßen. Voraussetzung dafür ist, dass die Restmasse unterhalb eines Schwellenwertes von 1,44 Sonnenmassen (M_☉) bleibt, der sogenannten Chandrasekhar-Grenze. Andernfalls entsteht nach einem Supernova-Ausbruch ein Neutronenstern oder (bei einer Kernmasse von mehr als 2½ M_☉) gar ein Schwarzes Loch. Neutronensterne und Schwarze Löcher setzen relativ massive stellare Vorgänger voraus mit mindestens etwa 8 M_☉, da die Sterne gegen Ende ihrer Existenz einen hohen Masseverlust erleiden. Daher erreicht die Kernmasse entsprechend selten die benötigten 1,44 M_☉, um ein anderes Objekt als einen Weißen Zwerg entstehen zu lassen.

Geschichtliches

Der zuerst entdeckte, aber nicht als solcher erkannte Weiße Zwerg war 40 Eridani B im Dreifachsternsystem 40 Eridani. Das Sternpaar 40 Eridani B/C wurde von William Herschel am 31. Januar 1783 entdeckt und erneut von Friedrich Georg Wilhelm Struve im Jahre 1825 sowie von Otto Wilhelm von Struve im Jahr 1851 (siehe Van Den Bos, W. H. und Heintz, W. D.). Im Jahre 1910 entdeckten Henry Norris Russell, Edward Charles Pickering und Williamina Fleming, dass obgleich 40 Eridani B ein sonnennaher schwacher Stern ist, die üblicherweise Rote Zwergsonnen sind, er vom Spektraltyp A und somit weiß ist (siehe Holberg, J. B.).

Im Jahre 1914 hat Walter Adams den Spektraltyp von 40 Eridani B offiziell kommuniziert.

Der nächstgelegene Weiße Zwerg ist Sirius B, der winzige Begleiter des Sirius, der mit −1,5^m den hellsten Stern am Nachthimmel darstellt. Der 8,5 Lichtjahre entfernte, sehr heiße Sirius hat 2 Sonnenmassen und ist 22-mal heller als die Sonne. Sirius B (8,7^m) hat zwar nur Erdgröße, aber 98 Prozent der Sonnenmasse und 2 Prozent ihrer Leuchtkraft. Er ist der bestuntersuchte Stern dieses Typs. Ein Teelöffel voll seiner Materie hätte eine Masse von über 5 Tonnen.

Entdeckt wurde er 1844 indirekt durch winzige Unregelmäßigkeiten in der Eigenbewegung des Sirius, aus denen Friedrich Bessel auf einen Doppelstern mit etwa 50 Jahren Umlaufzeit schloss. Teleskopisch konnte Sirius B erst 1862 nachgewiesen werden, weil er vom 10.000-mal helleren Hauptstern in 3" bis 10" Winkelabstand völlig überstrahlt wird. Alvan Graham Clark gelang dies bei der Prüfung eines neuen, langbrennweitigen Objektivs. Weil sich Sirius B damals auf seiner Ellipsenbahn zunehmend von Sirius A entfernte, konnte er bald auch von anderen Beobachtern beobachtet werden.

Im Jahre 1917 entdeckte Adriaan van Maanen den sogenannten Van Maanens Stern. Er ist ein isolierter Weißer Zwerg im Abstand von 13,9 Lichtjahren. Diese drei Weißen Zwerge sind die drei zuerst entdeckten Weißen Zwerge und werden auch als die klassischen Weißen Zwerge bezeichnet.

Der zweitnächste Weiße Zwerg wurde 1896 als Begleiter des Prokyon (Nr. 18) in 11½ Lichtjahren entdeckt. Prokyon B hat nur 11. Größe und ist wegen seiner engen Bahn (3" ≈ 0,001°) und größeren Helligkeitsdifferenz erst in großen Teleskopen sichtbar. Trotz 0,6 Sonnenmassen ist er etwas größer als Sirius B.

Dieser seltsame Umstand erklärt sich heute durch die Theorie der entarteten Materie: Je größer diese hunderttausende Grad heiße Sternmasse, desto mehr wird sie zusammengepresst. Eine Beobachtung jüngeren Datums ist auch, dass manche Weißen Zwerge als Folge der Strahlungsgesetze im Röntgen- und UV-Licht heller als ihr Hauptstern sein können.

Sei auch der Weiße Zwerg GJ 440 (LP 145-141) vom Südhimmel im Abstand von 15 Lichtjahren genannt, der als Stern mindestens seit 1917 bekannt ist, als seine Eigenbewegung von R.T.A. Innes und H.E. Wood publiziert wurde; er ist der viertnächste bekannte Weiße Zwerg nach dem Sirius B, Procyon B und dem Van Maanens Stern. Auch er ist ein isolierter Weißer Zwerg.

Stein 2051 B ist der sechstnächste Weiße Zwerg von der Sonne, er befindet sich im Abstand von 18 Lichtjahren. Im Jahr 2017 wurde er beobachtet, als er vor einem weiter entfernten Stern vorüberzog (siehe Sahu et al.). Die Beugung des Sternenlichtes durch das Gravitationsfeld des näher gelegenen Weißen Zwerges ermöglichte die direkte Messung seiner Masse, die sich zu 0,675 ± 0,051 Sonnenmassen ergibt. Dies ist konsistent zur theoretischen Modellierung eines Weißen Zwerges mit Kohlenstoff-Sauerstoff Kern. Stein 2051 B ist erst der vierte Weiße Zwerg, bei dem eine direkte Messung von Masse und Durchmesser möglich war, neben den sonnennahen Weißen Zwergen Sirius B, Procyon B sowie 40 Eridani B.

Schon im 18. Jahrhundert hatte man Planetarische Nebel entdeckt und ihnen den Namen wegen ihrer Ähnlichkeit zum Scheibchen des Uranus gegeben. Vor knapp hundert Jahren erkannte man, dass die manchmal sichtbaren Zentralsterne Weiße Zwerge sind, welche diesen Nebel als sterbender Roter Riese abgestoßen haben.

Bestimmung der Zustandsgrößen

Aus Spektrum und Helligkeit

Aus dem Spektrum und der beobachteten Helligkeit lassen sich einige wichtige Merkmale Weißer Zwerge ableiten. Kennt man die Entfernung eines solchen Sterns, zum Beispiel anhand der jährlichen Parallaxe, so gibt die gemessene Magnitude Auskunft über die wahre Leuchtkraft. Entfernung und Spektrum sind wegen der geringen Helligkeit allerdings nur bis etwa 500 Lichtjahre verlässlich feststellbar.

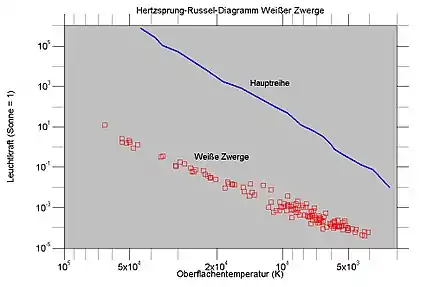
Das Spektrum wiederum zeigt die Oberflächentemperatur an. Zahlreiche solcher Beobachtungen sind bereits durchgeführt worden, als Beispiele seien die in nachfolgendem Diagramm dargestellten Ergebnisse von Bergeron et al. (2001) und Liebert et al. (2005) genannt. James William Liebert und seine Mitautoren untersuchten Weiße Zwerge hoher Oberflächentemperatur, also klassische Vertreter dieses Sterntyps, wohingegen Pierre Bergeron und Kollegen sich auf kühle Weiße Zwerge konzentrierten. Solche Objekte werden als alte Weiße Zwerge gedeutet, die bereits eine lange Abkühlungszeit von mehreren Milliarden Jahren hinter sich haben (siehe Abschnitt Energietransport).

Beide Arbeiten zeigen den für Weiße Zwerge typischen großen Leuchtkraftabstand zur Hauptreihe (letztere beruht auf den Angaben von Helmut Scheffler und Hans Elsässer (1990)). Bei sehr heißen Weißen Zwergen liegt das Leuchtkraftdefizit etwa bei einem Faktor 10⁵, bei sehr kühlen etwa bei einem Faktor von 10³. Bei gleicher Oberflächentemperatur entspricht dem Unterschied an Leuchtkraft ein gleich großer an Oberfläche. Weiße Zwerge haben also tausend- bis hunderttausendfach kleinere Oberflächen als Hauptreihensterne, das bedeutet 30- bis 300-fach kleinere Radien. Übliche Radien Weißer Zwergen liegen zwischen knapp einem und zweieinhalb Erdradien. Dieses kleine Volumen – nur etwa 10⁻⁶ bis 10⁻⁵ Sonnenvolumina – enthält aber etwa eine Sonnenmasse, was zu einer mittleren Dichte von etwa einer Tonne pro Kubikzentimeter führt. Mit einem kirschgroßen Stück eines Weißen Zwerges ließe sich also etwa ein Auto aufwiegen. Aus der enorm starken Massekonzentration folgt weiter eine sehr hohe Fallbeschleunigung an der Oberfläche. Die Oberflächenschwere ist der Masse eines Himmelskörpers direkt und dem Quadrat von dessen Radius umgekehrt proportional. Eine Sonnenmasse – entsprechend etwa 3 · 10⁵ Erdmassen – auf Erdvolumen komprimiert erzeugt eine Fallbeschleunigung auf der Oberfläche, die die der Erde um den Faktor 3 · 10⁵ übersteigt.

Aus Breite der Spektrallinien und Rotverschiebung

Um die Oberflächenschwere eines Sterns zu ermitteln, muss man dessen Masse jedoch keineswegs kennen, sie kann auch direkt aus dem Spektrum abgeleitet werden. Bei hoher Fallbeschleunigung unterliegt nicht nur das Sterninnere, sondern auch noch die Photosphäre einem hohen Druck, was aufgrund häufiger Stöße zwischen den Teilchen zu einer Verbreiterung der Spektrallinien führt (sogenannte Druckverbreiterung).

Die hohe Gravitation auf der Oberfläche Weißer Zwerge zieht noch einen weiteren, für die Untersuchung solcher Sterne äußerst nützlichen Effekt nach sich. Nach der Allgemeinen Relativitätstheorie tritt eine klar messbare Rotverschiebung auf (siehe zum Beispiel Greenstein et al. (1971)). In der Praxis tritt jedoch aufgrund der Eigenbewegung des Sterns eine zusätzliche Wellenlängenverschiebung der Spektrallinien hinzu, welche vom Dopplereffekt herrührt.

Die von der Oberflächenschwere herrührende Rotverschiebung ist direkt proportional zur Hubarbeit, welche das Licht gegen das Gravitationsfeld verrichten muss. Diese aber ist wieder direkt proportional der Masse des Sterns und umgekehrt proportional zu dessen Radius. Kombiniert man dies mit der Fallbeschleunigung – welche ja ebenfalls von der Masse und dem Radius des Sterns abhängt – so lassen sich diese beiden Größen einzeln bestimmen.

Beispiel Sirius B

Ein typischer Weißer Zwerg ist Sirius B, der Begleiter des Sirius. Obwohl schon lange als ungewöhnliches Objekt identifiziert, ist er weiterhin Gegenstand von Untersuchungen. Seine Eigenbewegung ist genau bekannt, so dass die Wellenlängenverschiebungen durch den Dopplereffekt und die Rotverschiebung im Schwerefeld sicher getrennt werden können. Ebenso ist seine Entfernung genau bekannt, so dass Helligkeitsmessungen eine sichere Auskunft über die Leuchtkraft geben.

Eine aktuelle Untersuchung stammt von Barstow et al. (2005), welche Sirius B mit dem Hubble Space Telescope beobachteten. Dieses ist aufgrund seines sehr hohen Auflösungsvermögens in der Lage, Sirius B von dem sehr viel helleren, nur wenige Bogensekunden entfernt stehenden Hauptstern zu trennen.

Die Autoren geben für Sirius B eine Oberflächentemperatur von etwa 25.200 K an. Während ein so heißer Hauptreihenstern normalerweise etwa 10.000fach lichtstärker als die Sonne ist, ist Sirius B aber etwa 450-mal lichtschwächer als diese. Im sichtbaren Bereich liegt Sirius B gerade einmal bei der Größenklasse 11,43, wohingegen es die Sonne auf die Größenklasse 4,83 bringt. Für den Radius von Sirius B finden Barstow et al. (2005) auf Grundlage der Rotverschiebung einen Wert von etwa 0,00864 Sonnenradien, was 6000 km entspricht. Er ist damit etwa so groß wie die Erde. Dennoch weist er ca. 0,978 Sonnenmassen auf. Die Oberflächenschwere ist den Autoren zufolge etwa 375.000-mal größer als auf der Erde. Die von Barstow et al. (2005) gemessene Rotverschiebung aufgrund der Gravitation ist gleichwertig einer Dopplerverschiebung bei einer Geschwindigkeit von etwa 80 km/s. In dem von den Autoren untersuchten Bereich von 380 bis 510 nm beträgt die entsprechende Wellenlängenverschiebung etwa 0,1 nm, ein geringer, aber mit einem hochauflösenden Spektrographen leicht nachweisbarer Wert.

Klassifizierung von Weißen Zwergen

Weiße Zwerge werden üblicherweise mit eigenen Klassen klassifiziert, es werden also nicht die normalen Spektralklassen verwendet, sondern solche mit einem Präfix D (für Degeneriert). Siehe → Klassifizierung der Sterne#Spektralklassen außerhalb der Standardsequenzen.

Innerer Aufbau

Innerer Aufbau Weißer Zwerge der Spektralklassen DA, DB, DO und PG 1159.

Methoden der Modellierung

Um ein genaues Modell eines Weißen Zwerges zu gewinnen, muss man ein ähnliches Gleichungssystem betrachten wie unter dem Artikel Sternaufbau für Hauptreihensterne diskutiert (siehe dazu zum Beispiel die Lehrbücher von Scheffler und Elsässer (1990) oder von Sexl (1979)). Die Gleichungen für Masseerhaltung und hydrostatisches Gleichgewicht dürfen hierbei unverändert übernommen werden, und damit auch die qualitativen Zusammenhänge zwischen Sternmasse $M$ , Sternradius $R$ , Dichte $\rho$ und zentralem Druck $p_{\mathrm {c} }$ , welche aus dem Lösen der Gleichungen unter der Annahme einer konstanten Sterndichte folgen:

\rho \propto {\frac {M}{R^{3}}}

p_{\mathrm {c} }\propto {\frac {M^{2}}{R^{4}}}

Viele der nun skizzierten Modelle beruhen aber nicht nur auf den Grundgleichungen des Sternaufbaus, sondern nutzen auch die Tatsache aus, dass manche Weiße Zwerge pulsieren. Dies macht sich durch Helligkeitsschwankungen bemerkbar, die aufgrund ihrer oft kurzen Zeitskala von Minuten gut verfolgt werden können. So wie bei Erdbeben der Gesteinsuntergrund bestimmte Schwingungsfrequenzen passieren lässt, andere hingegen wegfiltert, werden aufgrund der inneren Struktur des Sterns bestimmte Zeitskalen der Pulsation bevorzugt. Diese Methode wird daher in Analogie zur irdischen Erdbebenforschung als Asteroseismologie bezeichnet.

Materieverteilung in Weißen Zwergen

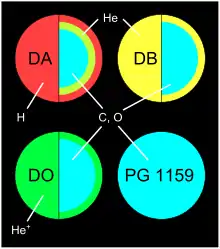
Realistische Szenarien für die Verteilung der Materie in Weißen Zwergen liefern zum Beispiel die Arbeiten von Corsico et al. (2001), Althaus et al. (2004) und Althaus et al. (2005). Während im Stadium des Roten Riesen aufgrund weiträumiger Konvektionsströmungen eine erhebliche Durchmischung des Sterninneren auftreten kann, werden in einem Weißen Zwerg die chemischen Elemente sehr stark nach ihrem Atomgewicht getrennt. Ohne nukleare Energieerzeugung stellt sich laut Hansen (2004) im Kern kein ausreichendes Temperaturgefälle mehr ein, um die Konvektion dort noch aufrechtzuerhalten. Somit können die schweren Atomkerne relativ ungestört zum Zentrum hin absinken. Es bildet sich ein Kern heraus, dessen innerer Teil nach Corsico et al. (2001) von Sauerstoff und dessen äußerer Teil von Kohlenstoff dominiert wird. Leichtere Elemente fehlen im Kern nahezu ganz.

Nach außen schließt sich eine Schicht an, die fast nur Helium enthält. Diese muss man sich als dünn vorstellen, gemäß den hier zitierten Arbeiten beträgt ihre Masse nur etwa 10⁻⁴ bis 10⁻² Sonnenmassen. Bei etwa 20 Prozent aller Weißen Zwerge bildet die Heliumschicht die äußerste Zone. Etwa 80 Prozent aller Weißen Zwerge besitzen jedoch zusätzlich eine Schicht aus praktisch reinem Wasserstoff. Diese ist noch dünner als die Heliumschicht, ihre Masse liegt nur bei etwa 10⁻⁶ bis 10⁻⁴ Sonnenmassen. Nahezu die gesamte Masse ist im Sauerstoff-Kohlenstoff-Kern vereint.

Dass die Photosphäre eines Weißen Zwerges sehr dünn sein muss, wird klar, wenn man die ungeheure Oberflächenschwere auf die barometrische Höhenformel anwendet. Diese besagt, dass der Atmosphärendruck exponentiell mit einer Skalenhöhe

H={\frac {k_{\mathrm {B} }T}{mg}}

nach außen abfällt bzw. nach innen ansteigt. Setzt man für $m$ die Atommasse von Wasserstoff, und für die Oberflächentemperatur $T$ und Fallbeschleunigung $g$ die Werte von Sirius B ein, so erhält man eine Skalenhöhe von nur 56 m (k_B steht für die Boltzmann-Konstante). Dieses Ergebnis besagt, dass mit zunehmender Tiefe auf einer Längenskala von kaum mehr als 100 m der Druck auf das Zehnfache ansteigt. Schon in einer Tiefe von nur wenigen Kilometern ist also eine enorme Verdichtung der Materie erreicht.

Besondere Typen

Nicht alle Weißen Zwerge folgen dem hier skizzierten Aufbau. Einige Sterne dieses Typs besitzen keinen Kern aus Sauerstoff und Kohlenstoff, sondern nur aus Helium. Diese Objekte widersprechen scheinbar der gängigen Theorie der Sternentwicklung. Einzelsterne, bei denen im Verlauf ihrer Entwicklung die Fusion von Helium zu Kohlenstoff ausbleibt, weisen Scheffler und Elsässer (1990) zufolge eine Masse von maximal 0,5 Sonnenmassen auf. Die Lebensdauer solch massearmer Sterne liegt aber bei mindestens 20 Milliarden Jahren, so dass sich aus solchen noch gar keine Weißen Zwerge gebildet haben können. Nach Althaus und Benvenuto (1997) sowie Serenelli et al. (2002) ist in sehr engen Doppelsternsystemen aber eine genügend schnelle Entstehung von heliumdominierten Weißen Zwergen möglich. In solchen Systemen üben die Sterne starke Gezeitenkräfte aufeinander aus, was in der Phase des Aufblähens zum Roten Riesen einen hohen Masseverlust nach sich ziehen kann. Auf diese Weise kann auch die Entwicklung eines relativ massereichen, das heißt ausreichend kurzlebigen Sterns, in einen Weißen Zwerg mit Heliumkern münden.

Umgekehrt wurden 2007 Weiße Zwerge gefunden, die nur noch aus Kohlenstoff (und Sauerstoff) bestehen, also auch keine Heliumhülle mehr besitzen. Diese Objekte wurden erstmals von Dufour et al. (2007) beschrieben und als DQ-Typ vorgeschlagen.[1] Montgomery et al. (2008) führten erste detaillierte Berechnungen durch, in welchen sie das Objekt SDSS J142625.71+575218.3 (V430 Ursae Majoris) als Prototyp der neuen Sternklasse definierten.[2] Zudem zeigten sie, dass auch diese Sterne pulsieren können.[3] Althaus et al. (2009) schlugen bereits einen Mechanismus vor, der das Fehlen der Heliumschicht erklären könnte.[4] Wie im Abschnitt „instabile Weiße Zwerge“ beschrieben wird, können sich Weiße Zwerge unter bestimmten Bedingungen wieder in Riesen verwandeln. Bei diesem zweiten Durchlauf eines Riesenstadiums büßen die Sterne die Heliumhülle ein.

Zustandsgleichung

Die Bewegungsenergie eines Teilchens in einem Hauptreihenstern ist überwiegend thermische Energie, so dass als Zustandsgleichung die allgemeine Gasgleichung verwendet werden darf. In einem Weißen Zwerg tritt aufgrund der hohen Dichte eine nicht thermische Komponente hinzu, die auf einem quantenmechanischen Effekt beruht. Dies führt zu einer besonderen Zustandsgleichung, bei welcher der Druck nur noch von der Dichte, aber nicht mehr von der Temperatur abhängt. Man bezeichnet einen solchen Zustand als entartet.

Fermienergie eines Teilchens

Durch die starke Verdichtung der Materie in einem Weißen Zwerg rücken dort die Teilchen im Mittel enger zusammen. Sperrt man aber ein Teilchen auf eine Längenskala $x$ ein, so bekommt dieses nach der Heisenbergschen Unschärferelation einen Impuls

p_{F}={\frac {h}{2\pi x}},

der als Fermiimpuls bezeichnet wird. $h$ bezeichnet das Planck’sche Wirkungsquantum.

Bei nicht zu kleiner Längenskala ist die aus dem Fermiimpuls resultierende Geschwindigkeit klein gegenüber der Lichtgeschwindigkeit $c$ , so dass man für die entsprechende Bewegungsenergie, die sogenannte Fermienergie, schreiben darf:

E_{F}={\frac {p_{F}^{2}}{2m}}={\frac {h^{2}}{8\pi ^{2}mx^{2}}}.

Da die Teilchenmasse $m$ im Nenner erscheint, ist sofort klar, dass die Fermienergie der Elektronen um ein Mehrtausendfaches größer ist als diejenige der sehr viel schwereren Atomkerne. Elektronen aber gehören der Teilchenklasse der Fermionen an, welche nach dem Pauli-Prinzip dem „Einsperren“ einen Widerstand entgegensetzen.

Dieses besagt, dass sich maximal zwei Elektronen des Sternplasmas im selben energetischen Zustand befinden können. Die möglichen Energiezustände kann man sich anschaulich als eine Leiter vorstellen, deren Sprossenabstand bei Verringerung des Sternvolumens, das heißt mit kleiner werdendem $x$ , wächst. Da die Zustände vom unteren Ende der Leiter an besetzt werden, muss bei einer Kompression den Elektronen so viel Energie zugeführt werden, dass sie auf Anhieb an das obere Ende der Leiter gelangen können. Dies führt zu einem Gegendruck, welcher bis zu der bereits erwähnten Chandrasekhar-Grenze der Gravitation standhalten kann.

Bei sehr kleiner Längenskala kann die Geschwindigkeit der Elektronen der Lichtgeschwindigkeit nahekommen, so dass dann die Fermienergie relativistisch berechnet werden muss. Im Extremfall, bei dem die Bewegungsgeschwindigkeit fast der Lichtgeschwindigkeit entspricht, gilt:

E_{F}=p_{F}c={\frac {hc}{2\pi x}}.

Entartung liegt vor, falls die Fermienergie gegenüber der thermischen Energie dominiert. Um dies zu überprüfen, muss noch die Längenskala $x$ ausgewertet werden. Es gilt:

x^{3}={\frac {1}{n_{e}}}={\frac {\mu m_{p}}{\rho }}.

$n_{e}$ ist hier die Teilchendichte der Elektronen, $\mu$ die mittlere molare Masse der Sternmaterie (nicht der Atomkerne) und $m_{p}$ die Masse des Protons. Einsetzen liefert für die Fermienergie im nicht relativistischen Fall:

E_{F}={\frac {h^{2}}{8\pi ^{2}m_{e}}}\left({\frac {\rho }{\mu m_{p}}}\right)^{\frac {2}{3}}=4{,}323\cdot 10^{-21}\left({\frac {\rho }{\mu }}\right)^{\frac {2}{3}}.

Im (extrem) relativistischen Fall gilt:

E_{F}={\frac {hc}{2\pi }}\left({\frac {\rho }{\mu m_{p}}}\right)^{\frac {1}{3}}=2{,}663\cdot 10^{-17}\left({\frac {\rho }{\mu }}\right)^{\frac {1}{3}}.

In beiden Fällen ist die Dichte in kg/m³ einzusetzen, die molare Masse als Vielfaches der atomaren Masseneinheit. Die Fermienergie ist dann in Joule gegeben.

In Wahrheit haben nicht alle Elektronen genau die gleiche Energie $E_{F}$ . Die verschiedenen Energien folgen vielmehr einer bestimmten Verteilung, der sogenannten Fermi-Dirac-Verteilung. Für die nachfolgende Diskussion ist die hier vorgestellte elementare Theorie aber ausreichend genau.

Unter nicht relativistischen Bedingungen wächst die Fermienergie rascher mit zunehmender Dichte an als bei relativistischen Verhältnissen. Im ersten Fall nehmen mit zunehmender Kompression sowohl der Impuls als auch die Geschwindigkeit zu (so dass letztlich eine umgekehrt quadratische Abhängigkeit von $x$ vorliegt), im zweiten aber wegen der Grenzgeschwindigkeit $c$ nur noch der Impuls (was eine lediglich umgekehrt proportionale Abhängigkeit von $x$ zur Folge hat).

Die thermische Energie eines Plasmateilchen folgt wie üblich der Beziehung

E_{\mathrm {th} }={\frac {3}{2}}k_{\mathrm {B} }T,

wobei $k_{\mathrm {B} }$ die Boltzmann-Konstante bezeichnet.

Beispiele von Entartung

Nach Hansen (2004) liegt die zentrale Dichte eines weißen Zwerges in der Größenordnung von 10¹⁰ kg/m³ und die zentrale Temperatur kurz nach dem Ende des Rote-Riesen-Stadiums in der Größenordnung von 10⁸ K. Die mittlere molare Masse eines von Kohlenstoff dominierten, vollständig ionisierten Kerns liegt bei etwa 12. Damit ergibt sich (nach nicht relativistischer Rechnung) eine Fermienergie von etwa 1,3 · 10⁻¹⁴ J, und eine thermische Energie von etwa 2,1 · 10⁻¹⁵ J. In einem gerade erst entstandenen weißen Zwerg darf letztere also noch nicht vernachlässigt werden. Allerdings kühlt ein solcher ohne nukleare Energiequellen ab, so dass Hansen zufolge (2004) nach etwa 10⁸ Jahren nur noch eine Zentraltemperatur von etwa 10⁷ K zu erwarten ist. Dann ist ein klares Übergewicht der Fermienergie gegeben.

Weiße Zwerge sind nicht das einzige Beispiel für durch die Fermienergie dominierte Materie. Betrachtet man zum Beispiel irdisches Eisen, so erhält man mit einer Dichte von 8000 kg/m³ und einer mittleren molaren Masse von 56 (ein Eisenion und zwei freie Elektronen) eine Fermienergie von etwa 2,4 · 10⁻¹⁹ J. Bei 293 K (20 °C) liegt die thermische Energie etwa bei 6,1 · 10⁻²¹ J. Die Fermienergie behält also klar die Oberhand, die irdischen Metallelektronen sind ebenso entartet wie diejenigen in einem weißen Zwerg. Diese Objekte sind trotz ihrer extremen Dichte somit gar nicht so exotisch, man darf sie sich zumindest teilweise als metallähnliche Körper vorstellen.

Zusammenhang zwischen Druck und Dichte

Die allgemeine Gasgleichung $p=nk_{\mathrm {B} }T$ legt wegen $E_{\mathrm {th} }={\frac {3}{2}}k_{\mathrm {B} }T$ den Zusammenhang

p={\frac {2}{3}}nE

nahe. Dieser gilt auch für entartete Materie. Einsetzen der Fermienergie liefert im nicht relativistischen Fall:

p={\frac {h^{2}}{12\pi ^{2}m_{e}}}\left({\frac {\rho }{\mu m_{p}}}\right)^{\frac {5}{3}}=1{,}726\cdot 10^{6}\left({\frac {\rho }{\mu }}\right)^{\frac {5}{3}}

Im (extrem) relativistischen Fall ergibt sich:

p={\frac {hc}{3\pi }}\left({\frac {\rho }{\mu m_{p}}}\right)^{\frac {4}{3}}=1{,}061\cdot 10^{10}\left({\frac {\rho }{\mu }}\right)^{\frac {4}{3}}

Für die Dichte und die mittlere molare Masse sind die gleichen Einheiten wie oben zu verwenden, so dass dann der Druck in N/m² gegeben ist. Setzt man wiederum die Dichte mit 10¹⁰ kg/m³ und die mittlere molare Masse mit 2 an, so erhält man (nicht relativistisch) einen zentralen Druck von etwa 2,5 · 10²² N/m², was ziemlich genau um das Millionenfache über dem zentralen Sonnendruck liegt. Angesichts der Proportionalität $p_{\mathrm {c} }\propto R^{-4}$ ist ein derart hoher Druck im Inneren eines weißen Zwergs normal.

Das unterschiedliche Verhalten der Fermienergie im nicht relativistischen und relativistischen Fall schlägt sich auch in der Zustandsgleichung nieder. Bei nicht relativistischen Teilchen steigt der Druck rascher mit der Dichte an als bei relativistischen. Erstere können zusätzlichem Gravitationsdruck daher besser standhalten als zweitere. Wie nun gezeigt wird, liegt genau hier die Existenz einer Grenzmasse für Weiße Zwerge begründet.

Schlussfolgerungen

Durch das Verschwinden der Temperatur aus der Zustandsgleichung bildet diese zusammen mit den Gleichungen für Masseerhaltung und hydrostatisches Gleichgewicht schon ein geschlossenes Gleichungssystem. Die Dichte- und Druckschichtung kann nun unabhängig von der Temperaturschichtung und damit dem Energietransport behandelt werden. Es besteht ein direkter Zusammenhang zwischen Sternmasse und -radius bzw. -dichte. Setzt man die oben gegebenen Proportionalitäten zwischen $M$ , $R$ , $\rho$ und $p_{\mathrm {c} }$ in die nicht relativistische Zustandsgleichung ein, so erhält man nach kurzer Rechnung:

R\propto M^{-1/3}

M\propto \rho ^{1/2}

Je massereicher ein Weißer Zwerg, umso kleiner ist er. Ein Hauptreihenstern hingegen ist mit mehr Masse auch größer, als es der Erwartung entspricht. Mit zunehmender Masse werden Weiße Zwerge dichter. Dies bedeutet zugleich auch, dass nicht relativistische Elektronen einer größeren Masse standhalten können, falls sie stärker komprimiert werden. Tritt eine Störung des Druckgleichgewichtes in Richtung höherer Dichte auf, treibt der steigende Fermidruck das System wieder in den Ausgangszustand zurück.

Verwendet man die relativistische Zustandsgleichung, so ergeben sich folgende Beziehungen:

R\propto M^{2/3}

M\propto \rho ^{-1}

Relativistische Weiße Zwerge müssten mit zunehmender Masse größer und weniger dicht werden. Eine solche Konfiguration aber ist nicht stabil. Werden relativistische Elektronen dichter gepackt, können sie weniger Masse tragen als vorher. Im Falle einer Störung kann der zusätzliche Fermidruck das Mehr an Gravitationsdruck nicht ausgleichen. Die Kompression setzt sich fort, bis mit einem Neutronenstern oder schwarzen Loch ein neuer Gleichgewichtszustand erreicht ist.

Somit gibt es eine Massengrenze für Weiße Zwerge. Diese ist erreicht, wenn infolge einer zu hohen Dichte die Elektronen relativistisch werden und damit die Zustandsgleichung $p=p(\rho )$ entscheidend abflacht.

Achsenbeschriftung fehlerhaft, keine Prozente, sondern Anteile vom Ganzen

In die Zustandsgleichung und damit auch in Masse und Radius eines Weißen Zwerges gehen das Plancksche Wirkungsquantum und die Massen von Elektron und Proton ein. Das bedeutet, dass hier astronomische Größen direkte Funktionen von mikrokosmischen Naturkonstanten sind.

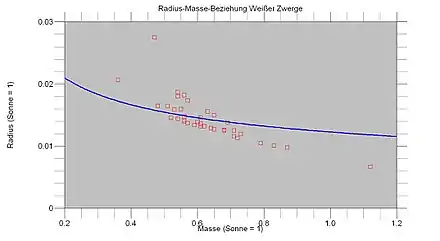
Zuletzt sei wieder ein Beispiel aus der Beobachtungspraxis gezeigt. Liebert et al. (2005) bestimmten aus Leuchtkräften und Oberflächentemperaturen Weißer Zwerge (siehe obiges Hertzsprung-Russell-Diagramm) mittels des Stefan-Boltzmann-Gesetzes deren Radien. Zusätzlich leiteten sie aus den Spektren der Sterne deren Oberflächenschweren ab, so dass sie unter Hinzunahme der Radien auch deren Massen bestimmen konnten.

Die Beobachtungen zeigen eine klare Abnahme des Sternradius mit zunehmender Masse und stellen damit eine eindeutige Bestätigung des Konzepts der entarteten Materie dar. Das elementare Gesetz $R\propto M^{-1/3}$ stimmt mit den Messungen recht gut überein. Bei dem sehr stark abweichenden Objekt handelt es sich um einen besonders heißen Stern, dessen Oberflächentemperatur 65.000 K beträgt. Wie bereits gezeigt, darf bei sehr heißen Weißen Zwergen die thermische Energie gegenüber der Fermienergie nicht vernachlässigt werden, so dass die Annahme vollständig entarteter Materie nicht mehr zulässig ist.

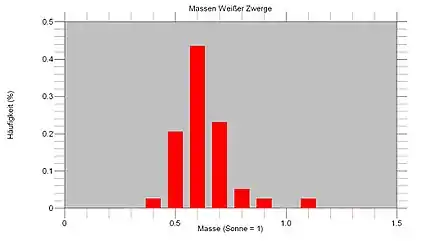
Bemerkenswert ist die Massenverteilung Weißer Zwerge. Fast alle der von Liebert et al. (2005) untersuchten Weißen Zwerge fallen in einen sehr schmalen Bereich von 0,5 bis 0,7 Sonnenmassen. Hier handelt es sich keineswegs um einen Sonderfall, das seltene Auftreten von sowohl sehr massearmen als auch relativ massereichen Weißen Zwergen wurde bereits von zahlreichen Beobachtungen bestätigt. Trotz unterschiedlicher Ausgangsmassen mündet die Entwicklung sonnenähnlicher Sterne nahezu in die gleiche Endmasse ein.

Energietransport

Während in Hauptreihensternen und auch in Riesen der Energietransport durch Strahlung und Konvektion erfolgt, dominiert in Weißen Zwergen die Wärmeleitung durch die Elektronen. Die sonst üblichen Mechanismen bleiben allein den dünnen, nicht entarteten Außenschichten vorbehalten.

Wärmeleitung

Die Wärmeleitung kann formal durch die gleiche Beziehung beschrieben werden wie der unter Sternaufbau skizzierte Energietransport durch Strahlung:

{\frac {\mathrm {d} T}{\mathrm {d} r}}=-{\frac {1}{K(r)}}{\frac {L(r)}{4\pi r^{2}}}

K(r) bezeichnet jetzt aber nicht das Strahlungsleitvermögen, sondern die Wärmeleitfähigkeit. Die Wärmeleitung im entarteten Kern ist so wirksam, dass in diesem näherungsweise überall die gleiche Temperatur vorliegt. Da die äußeren Schichten sehr dünn sind, darf zudem der Kernradius dem Sternradius gleichgesetzt werden. Damit vereinfacht sich obige Gleichung zu:

{\frac {T_{\mathrm {c} }}{R}}=-{\frac {1}{K}}{\frac {L}{4\pi R^{2}}}

$T_{\mathrm {c} }$ bezeichnet die Temperatur im Kern. Um die Leuchtkraft $L$ allein als Funktion der Kerntemperatur beschreiben zu können, muss die Abhängigkeit der Wärmeleitfähigkeit von der Temperatur und Dichte bekannt sein. Die Tatsache, dass die irdischen Metallelektronen ebenso entartet sind wie diejenigen in einem Weißen Zwerg, erweist sich dabei als außerordentlich nützlich. Der von irdischen Metallen bekannte Zusammenhang

K\propto \rho T

darf näherungsweise auch für Weiße Zwerge verwendet werden. Damit vereinfacht sich obige Gleichung weiter zu

L\propto R\rho T_{\mathrm {c} }^{2}

Der Sternradius ist, wie bereits unter dem Abschnitt Zustandsgleichung erläutert, allein durch die Masse des Weißen Zwerges eindeutig festgelegt. Die Dichte lässt sich durch den Ansatz eliminieren, dass es im Übergangsbereich zwischen Kern und Außenschicht eine Zone geben muss, wo der thermische Gasdruck $p_{\mathrm {th} }$ genau gleich dem Entartungsdruck $p_{\mathrm {e} }$ der Elektronen ist. Für den Gasdruck liefert die allgemeine Gasgleichung den Zusammenhang $p_{\mathrm {th} }\propto \rho T$ , für den Elektronendruck die im vorausgegangenen Abschnitt abgeleitete Zustandsgleichung die Beziehung $p_{\mathrm {e} }\propto \rho ^{5/3}$ . Das Gleichsetzen der beiden Drücke liefert $\rho \propto T^{3/2}$ , womit sich schließlich der folgende, bereits von Schwarzschild erkannte Zusammenhang ergibt:

L\propto T_{\mathrm {c} }^{7/2}

Junge, sehr heiße Weiße Zwerge sind also durchaus noch sehr leuchtkräftig (man sehe zum Beispiel das obige Hertzsprung-Russell-Diagramm, wo das heißeste Objekt immerhin noch 10-mal stärker strahlt als die Sonne). Da sie aber über keine nukleare Energiequellen mehr verfügen, kühlen sie zunächst rasch ab. Weil mit fallender Zentraltemperatur die Leuchtkraft aber sehr steil zurückgeht, verlangsamt sich in der Folge der Abkühlungsprozess.

Strahlung und Konvektion

Diese beiden Mechanismen des Energietransports sind bei Weißen Zwergen auf die dünne Helium- und (falls vorhanden) Wasserstoffschicht beschränkt. Detaillierte Untersuchungen wie zum Beispiel von Hansen (2004) zeigen, dass dabei die Verhältnisse mit denjenigen in Hauptreihensternen durchaus vergleichbar sind. Solange die äußeren Schichten noch genügend heiß sind, erfolgt dort wie bei Hauptreihensternen der Energietransport durch Strahlung. Fällt die Oberflächentemperatur unter einen bestimmten Wert – nach Hansen (2004) etwa 12.000 K – bildet sich dort eine Konvektionszone aus. Mit fortschreitender Abkühlung reicht diese immer tiefer in den Stern hinab, bis sie schließlich auf den Kern trifft. Auch dieses Verhalten ist demjenigen von Hauptreihensternen analog.

Schlussfolgerungen

Der oben genannte Zusammenhang zwischen Leuchtkraft und Zentraltemperatur erlaubt es, die Abkühlung eines Weißen Zwerges in Abhängigkeit von der Zeit zu beschreiben. Die Leuchtkraft gibt direkt die Änderung der inneren Energie mit der Zeit $\mathrm {d} E/\mathrm {d} t$ an. Da die Energie wiederum der Temperatur direkt proportional ist, gilt $L\propto \mathrm {d} T_{\mathrm {c} }/\mathrm {d} t$ . Dies führt letztlich auf die Beziehung

{\frac {\mathrm {d} T_{\mathrm {c} }}{\mathrm {d} t}}\propto T_{\mathrm {c} }^{7/2}

Diese Gleichung kann elementar durch Trennung der Variablen gelöst werden. Es ergibt sich ein Gesetz der Form

T_{\mathrm {c} }(t)=\left({\frac {1}{a\cdot t+b}}\right)^{2/5}

wobei $a$ und $b$ Konstanten darstellen. In $a$ geht unter anderem die Sternmasse ein. $b$ ist so zu wählen, dass sich die Anfangstemperatur zur Zeit $t=0$ ergibt. Das Gesetz sagt eine zunächst schnelle und dann langsame Abkühlung voraus. Setzt man es in die Beziehung zwischen Leuchtkraft und Kerntemperatur ein, erhält man:

L(t)=\left({\frac {1}{a\cdot t+b}}\right)^{7/5}

$a$ und $b$ haben natürlich jetzt andere Werte als bei dem Temperaturtrend. Wegen der sehr starken Abhängigkeit der Leuchtkraft von der Zentraltemperatur wird ein anfänglich sehr rascher Leuchtkraftabfall vorhergesagt, der sich dann aber ebenfalls verlangsamt. Schließlich kann der Leuchtkrafttrend in das Gesetz von Stefan-Boltzmann eingesetzt werden, welches die Leuchtkraft gemäß $L\propto T_{\mathrm {ober} }^{4}$ mit der Oberflächentemperatur $T_{\mathrm {ober} }$ verknüpft:

T_{\mathrm {ober} }(t)=\left({\frac {1}{a\cdot t+b}}\right)^{7/20}

Die Oberflächentemperatur folgt also fast dem gleichen Trend wie die Kerntemperatur.

Folgende Abbildungen vergleichen die von der elementaren Theorie vorhergesagten Trends mit modernen Modellen, wie sie zum Beispiel von Chabrier et al. (2000) entwickelt wurden. Bis zu einer Abkühlungszeit von etwa 5 Milliarden Jahren stimmen die einfachen Trends mit den exakten Berechnungen recht gut überein. Dann aber sagen die modernen Modelle eine neuerliche Beschleunigung der Abkühlung voraus. Dies liegt unter anderem darin begründet, dass die elementare Theorie eine direkte Proportionalität zwischen innerer Energie und Temperatur, also eine von der Temperatur unabhängige Wärmekapazität $C$ annimmt. Tatsächlich aber nimmt bei einem Festkörper unterhalb einer bestimmten Temperatur die Wärmekapazität mit derselben ab, es stellt sich das Gesetz von Debye ein, wonach $C\propto T^{3}$ . Ist die Abkühlung eines Weißen Zwergs sehr weit fortgeschritten, kann er daher die noch vorhandene Restwärme immer schlechter speichern und kühlt so trotz fallender Leuchtkraft wieder rascher aus.

Massereiche Weiße Zwerge kühlen zunächst langsamer aus als massearme. Erstere weisen einen höheren Energiegehalt auf und zugleich wegen ihrer kleineren Radien eine geringere Leuchtkraft. Bei weit fortgeschrittener Abkühlung kehrt sich unter anderem wegen der temperaturabhängigen Wärmekapazität die Situation teilweise jedoch um.

Die Abkühlungsmodelle Weißer Zwerge lassen sich durch Beobachtungen solcher Objekte in Sternhaufen überprüfen (siehe zum Beispiel Hansen (1999)). In jungen Sternhaufen finden sich entweder gar keine Weißen Zwerge (weil junge, massereiche Sterne weiter zum Neutronenstern oder gar Schwarzen Loch kollabieren) oder nur heiße, noch kaum ausgekühlte Objekte dieser Art. In alten Haufen hingegen sind sehr kühle Weiße Zwerge vorhanden.

Durch die Abkühlung bleibt ein solcher Stern nicht immer weiß, sondern nimmt im Laufe der Zeit eine zunächst gelbliche, dann rötliche und letztlich schwarze Färbung an. Wegen der enorm langen Zeitskalen konnten sich Weiße Zwerge jedoch bislang kaum unter eine Oberflächentemperatur von 4000 K abkühlen. Unabhängig von der Temperatur bleibt die Bezeichnung Weißer Zwerg aufgrund des großen Leuchtkraftdefizits im Vergleich zur Hauptreihe bestehen, zumal die Begriffe Gelber Zwerg und Roter Zwerg gerade für die entsprechenden Hauptreihensterne reserviert sind.

Instabile Weiße Zwerge

Obwohl Weiße Zwerge in ihrem Kern nicht mehr über nukleare Energiequellen verfügen, können sie durchaus noch eine erhebliche, ja eruptive Aktivität zeigen. Dies gilt vor allem dann, wenn sie Mitglieder enger Doppelsternsysteme sind.

Novae

Lange Zeit wurden Novae als leuchtschwache Abart der Supernovae betrachtet, als Sternexplosionen mit einem nicht ganz so extremen Helligkeitsausbruch. Erst in den 1970er Jahren wurde die allerdings bereits von Otto von Struve aufgestellte Hypothese bestätigt, dass der Ursprung einer Nova in einem sehr engen Doppelsternsystem zu suchen ist, das aus einem Weißen Zwerg und einem kühlen Hauptreihenstern besteht. Hier wird nur eine kurze Beschreibung des Phänomens gegeben, hinsichtlich der Einzelheiten sei auf den entsprechenden Artikel verwiesen.

In einem genügend engen Doppelsternsystem erstreckt sich der Hauptreihenstern bis zur Roche-Grenze, so dass Gas von diesem in den Anziehungsbereich des Weißen Zwerges gelangen kann. Es bildet sich ein permanenter Materiestrom und als Folge dessen eine Gasscheibe um den Weißen Zwerg herum aus. Diese macht sich durch ein Emissionsspektrum bemerkbar, das vor allem Linien des Wasserstoffs (Balmerserie), aber auch des Heliums aufweist.

Hat sich eine gewisse kritische Menge an Gas angesammelt, tritt ein explosionsartiges Wasserstoffbrennen auf. In dessen Verlauf wird die Gasscheibe abgestoßen (der Weiße Zwerg selbst explodiert jedoch nicht), was von einem enormen Helligkeitsausbruch begleitet ist. Nach dem Ausbruch kehrt das System zu seiner ursprünglichen Helligkeit zurück, und es kann sich eine neue Gasscheibe bilden. Auf diese Weise ist auch eine Wiederholung des Novageschehens mit von System zu System sehr unterschiedlichen Zeitabständen möglich.

Supernovae

Weiße Zwerge können charakteristische Supernovae auslösen. Die von einem Weißen Zwerg in einem engen Doppelsternsystem aufgesammelte Materie wird durch eine Nova nur teilweise abgestoßen, insbesondere bleiben durch das Wasserstoffbrennen erzeugte schwerere Kerne zurück. Dies bedeutet, dass seine Masse auf Kosten des Begleitsterns im Laufe der Zeit mehr und mehr zunimmt. Wird die Chandrasekhar-Grenze überschritten, beginnt der Weiße Zwerg zu kollabieren. Dabei setzt ein explosionsartiges Kohlenstoffbrennen ein, welches die Entstehung eines Neutronensterns unterbindet. Stattdessen detoniert der Weiße Zwerg vollständig, ohne einen Reststern zu hinterlassen, während der nun nicht mehr gravitativ gebundene Begleitstern davongeschleudert wird. Auch hier sei hinsichtlich der Einzelheiten auf den entsprechenden Artikel verwiesen.

Wiedergeborene Riesen

Am 20. Februar 1996 entdeckte der Japaner Yukio Sakurai im Sternbild Schütze einen „neuen“ Stern, der zunächst als Nova eingestuft wurde. Es stellte sich jedoch heraus, dass mit Sakurais Stern – auch als V4334 Sgr bezeichnet – ein extrem seltener Sterntyp zutage getreten war, für den es mit V605 Aql im Sternbild Adler und FG Sge im Sternbild Pfeil nur zwei weitere gesicherte Exemplare gibt.

Sakurais Stern war bei seiner Entdeckung ein Objekt etwa 11. Größe. Eine nachträgliche Überprüfung älterer photographischer Aufnahmen zeigte diesen dort als extrem schwach oder gar nicht nachweisbar an, d. h. vor dem Ausbruch lag seine Helligkeit unterhalb der 20. Größenklasse. Ein auf manchen dieser Aufnahmen extrem schwach angedeuteter Planetarischer Nebel konnte schon bald nach dem Helligkeitsausbruch von Duerbeck und Benetti (1996) bestätigt werden. Damit war gesichert, dass Sakurais Stern aus einem sehr jungen Weißen Zwerg hervorgegangen war.

Schon die ersten Spektren (siehe ebenfalls Duerbeck und Benetti (1996)) ließen erkennen, dass keine Nova vorlag. Sie zeigten eine Photosphäre mit abnorm schwachen Spektrallinien des Wasserstoffs, andererseits mit ungewöhnlich starken des Kohlenstoffs und Sauerstoffs. Damit war ausgeschlossen, dass der Helligkeitsausbruch durch das Wegsprengen einer Wasserstoffhülle hervorgerufen war. Trotz der Besonderheiten erinnerten die Spektren an Überriesen der Spektralklasse F.

Die Beobachtungen konnten rasch als sogenannter Helium-Flash gedeutet werden, worunter man ein explosionsartiges Einsetzen des Heliumbrennens in der Spätphase der Entwicklung sonnenähnlicher Sterne versteht. Zuerst ereignet sich dieses im Kern des bereits zum Roten Riesen gewordenen Sterns. Hat sich dort das Helium zu Kohlenstoff und Sauerstoff umgewandelt, treten Helium-Flashs auch in der sich dem Kern anschließenden Schicht auf. Ebendieses explosionsartig einsetzende Heliumschalenbrennen ist dafür verantwortlich, dass der Rote Riese seine Hülle weitestgehend abwirft. Sakurais Stern zeigt, dass ein Helium-Flash auch nach diesem Abwurf noch stattfinden kann, wenn der Stern schon unmittelbar vor der Abkühlungsphase als Weißer Zwerg steht. Damit aber wird aus diesem wieder ein Riese.

Diesem wiedergeborenen Giganten steht selbstverständlich nur noch eine geringe Menge an zu verbrennendem Helium zu Verfügung, so dass er sich nur kurze Zeit erneut in diesem Zustand behaupten kann. Die Entwicklung von Sakurais Stern seit 1996 liefert hierfür ein besonders extremes, in seiner Art erstmals beobachtetes Beispiel.

Schon bald nach seiner Entdeckung wurde Sakurais Stern erheblich röter, während seine visuelle Helligkeit zunächst stabil blieb. Dies deutete auf eine starke Abkühlung der Photosphäre hin. Spektren, wie sie z. B. von Arkhipova et al. (1998) aufgenommen wurden, zeigten zudem an, dass sich die Dominanz des Kohlenstoffs verstärkt hatte, sie waren nun zum Teil vollständig von molekularem Kohlenstoff dominiert.

Von Mitte 1998 an begann die visuelle Helligkeit des Sterns dramatisch abzufallen, bis Mitte 1999 war die 22. Größenklasse erreicht. Gleichzeitig stieg im Infraroten die Helligkeit sehr stark an. Offensichtlich hatte der Stern große Mengen an Kohlenstoff, Sauerstoff und anderen Elementen ausgestoßen, welche nun zu einer Staubhülle kondensierten, die praktisch alles sichtbare Licht absorbierte und die aufgenommene Energie im Infraroten wieder abgab (siehe Duerbeck (2002)). Diese Staubhülle verbirgt Sakurais Stern bis heute.

Indirekte Hinweise auf dessen weitere Entwicklung sind jedoch gegeben, z. B. in Form von Emissionslinien, die von ionisierten Elementen stammen. Zwar können auch Stoßwellen, die durch den Materieausstoß ausgelöst wurden, eine Ionisation innerhalb der Staubhülle bewirken. Van Hoof et al. (2007) legten jedoch dar, dass das beobachtete Ausmaß nur erklärt werden kann, wenn man zugleich von einer energiereichen Strahlung des Sterns ausgeht. Das aber bedeutet, dass er in den letzten Jahren wieder erheblich heißer geworden sein muss. Nur 13 Jahre nach der Wiedergeburt als Riese entwickelt er sich also abermals zum Weißen Zwerg.

V605 Aql, welcher um 1919 einen großen Helligkeitsausbruch zeigte, durchlief eine vergleichbar dramatische Entwicklung wie Sakurais Stern. Glücklicherweise existieren Spektren recht guter Qualität aus dieser Zeit (Lundmark (1921)), so dass sich zusammen mit modernen Messungen das seitdem erfolgte Geschehen rekonstruieren lässt (siehe Clayton und De Marco (1997)). Nicht ganz so rasch verläuft die Entwicklung von FG Sge, doch im Laufe der Jahrzehnte hat auch dieser Stern massive Variationen von Helligkeit, Farbe und Spektrum gezeigt (Lawlor and McDonald (2003)).

Sonstiges

Bedeutung der Gravitationsenergie

Nimmt man als Beispiel einen Stern mit einer Sonnenmasse, so hat dieser im Laufe seines Lebens (ca. 10 Milliarden Jahre) etwa 10⁴⁴ J durch Kernfusion umgesetzt, also etwa 10 Prozent seiner Sternmasse. In den letzten Minuten der Kontraktion des Sterns zum weißen Zwerg werden 10⁴³ J noch einmal durch die Gravitation freigesetzt[5], das entspricht ungefähr 10 Prozent der über die Lebensdauer verteilt abgestrahlten Energie.

Häufigkeit

Weiße Zwerge sind recht häufige Objekte. Laut Sion et al. (2009) finden sich im Umkreis von 20 Parsec um die Sonne insgesamt 129 derartige Sterne, was einem mittleren Abstand von etwa 6 Parsec bzw. etwa 19 Lichtjahren zwischen zwei Weißen Zwergen entspricht. Man schätzt, dass etwa 10 Prozent aller Sterne Weiße Zwerge sind. Insgesamt sind etwa 10.000 solcher Objekte bekannt. Durch systematische Himmelsdurchmusterungen wie den Sloan Digital Sky Survey wird diese Zahl aber schon in den nächsten Jahren stark ansteigen.

Weiße Zwerge aus massereichen Sternen?

Im Gegensatz zur vorherrschenden Theorie, wonach Weiße Zwerge nur aus relativ massearmen Sternen hervorgehen können, schlugen Meynet et al. (1994) folgendes spektakuläre Szenario vor: Weist ein sehr massereicher Stern (um die 100 Sonnenmassen) einen sehr hohen Anteil von Elementen schwerer als Helium auf (mehr als das Doppelte im Vergleich zur Sonne), so erleidet dieser im Verlauf seiner Entwicklung einen extremen Masseverlust. Der hohe Anteil schwerer Elemente macht die Sternmaterie weitgehend undurchsichtig, wodurch die Wirkung des ohnehin schon enormen Strahlungsdrucks noch verstärkt wird. Dadurch kann der Stern so viel Masse verlieren, dass er am Ende noch unterhalb der Chandrasekhar-Grenze bleibt. Diesem Szenario zufolge müsste es sehr junge Sternhaufen (welche an blauen, leuchtkräftigen Hauptreihensternen zu erkennen sind) mit Weißen Zwergen geben. Die Suche nach solchen Haufen ist bislang aber erfolglos geblieben.

Doppelsysteme Weißer Zwerge und Gravitationswellen

Enge Doppelsternsysteme von Weißen Zwergen wie HM Cancri stellen Quellen für Gravitationswellen dar, welche man mit dem zeitweise geplanten weltraumgestützten Gravitationswellendetektor LISA nachzuweisen hoffte (Stoerer und Veitch (2009)). Die von solchen Systemen abgestrahlten Gravitationswellen sollen durch ihre charakteristische Frequenz von anderen kompakten Quellen wie Pulsaren und Schwarzen Löchern unterscheidbar sein.

Planetensysteme Weißer Zwerge und deren potentielle Lebensfreundlichkeit

Im Jahre 2020 veröffentlichte das Fachmagazin Nature, dass Astronomen erstmals einen möglichen Gasriesen um einen weißen Zwerg (WD 1856 + 534b) entdeckt haben.[6] Er soll die Größe des Jupiter haben, jedoch die 14-fache Masse besitzen. Dies, aber auch bereits größere gefundene Mengen an Gestein, welche um Sternenleichen kreisen, lassen vermuten, dass auch Gesteinsplaneten um weiße Zwerge zu finden sein dürften. Diese könnten wohl mit dem Weltraumteleskop TESS entdeckt werden. Bei Erfolg soll dann an den Fundstellen mit dem James-Webb-Weltraumteleskop nach einem molekularen Nachweis für Biosignaturen gesucht werden, da laut der Forscher auch weiße Zwerge eine habitable Zone besitzen könnten, in denen Leben potentiell möglich ist.

Weitere Weiße Zwerge

Siehe auch

ZZ-Ceti-Stern, pulsierende Weiße Zwerge
Schwarzer Zwerg, erkaltete Weiße Zwerge: das Universum sollte noch zu jung sein für solche Objekte
Kataklysmische Veränderliche, Doppelsternsysteme mit einem akkretierenden Weißen Zwerg

Literatur

Adams, W. S.: An A-Type Star of Very Low Luminosity. In: Publications of the Astronomical Society of the Pacific. Nr. 26, 1914, S. 198 ff., doi:10.1086/122337.
Althaus L.G., Corsico A.H.: The Double-layered Chemical Structure in DB White Dwarfs. In: Astronomy and Astrophysics. Nr. 417, 2004, S. 1115 ff.
Althaus L.G., Miller Bertolami M.M., Corsico A.H., Garcia-Berro E., Gil-Pons P.: The Formation of DA White Dwarfs with Thin Hydrogen Envelopes. In: Astronomy and Astrophysics. 440 Letter, 2005, S. 1 ff.
Arkhipova V.P. et al.: Observations of Sakurai’s Object in 1997 and its Evolution in 1996–1997. In: Astronomy Letters. Nr. 24/2, 1998, S. 248 ff.
Barstow M.A., Bond H.E., Holberg J.B., Burleigh M.R., Hubeny I., Koester D.: Hubble Space Telescope Spectroscopy of the Balmer Lines in Sirius B. In: Monthly Notices of the Royal Astronomical Society. Nr. 362, 2005, S. 1134 ff.
Bergeron P., Legett S.K., Ruiz M.T: Photometric and Spectroscopic Analysis of Cool White Dwarfs with Trigonometric Parallax Measurements. In: Astrophysical Journal Supplement Series. Nr. 133, 2001, S. 413 ff.
Clayton G.C., De Marco O.: The Evolution of the Final Helium Shall Flash Star V605 Aql from 1917 to 1997. In: Astronomical Journal. Nr. 114/6, 1997, S. 2679 ff.
G. Chabrier, P. Brassard, G. Fontaine, D. Saumon: Cooling Sequences and Color-Magnitude Diagrams for Cool White Dwarfs with Hydrogen Atmospheres. In: Astrophysical Journal. Nr. 543, 2000, S. 216 ff.
Corsico A.H., Althaus L.G., Benvenuto O.G., Serenelli A.M.: New DA White Dwarf Evolutionary Models and their Pulsational Properties. In: Astronomy and Astrophysics. 380 Letter, 2001, S. 17 ff.
Duerbeck H.W.: The Final Helium Flash Object V4334 – An Overview. In: Astronomical Society of the Pacific Conference Series. Nr. 256, 2002, S. 237 ff.
Duerbeck H.W., Benetti S.: Sakurai’s Object – a Possible Final Helium Flash in a Planetary Nebula Nucleus. In: Astrophysical Journal. Nr. 468, 1996, S. L111 ff.
Greenstein J.L., Oke J.B., Shipman J.B., Shipman H.L.: Effective Temperature, Radius, and Gravitational Redshift of Sirius B. In: Astrophysical Journal. Nr. 169, 1971, 2005, S. 563 ff.
Hansen B.: Cooling Models for Old White Dwarfs. In: Astrophysical Journal. Nr. 520, 1999, S. 680 ff.
Hansen B.: The Astrophysics of Cool White Dwarfs. In: Physics Report. Nr. 399, 2004, S. 1 ff.
Heintz, W. D.: Astrometric study of four visual binaries. In: The Astronomical Journal. Nr. 79, 1974, S. 819 ff., doi:10.1086/111614.
Herschel, W.: Catalogue of Double Stars. By William Herschel, Esq. F. R. S. In: Philosophical Transactions of the Royal Society of London. Nr. 75, 1785, S. 40 ff. (royalsocietypublishing.org [PDF]).
Holberg, J. B.: How Degenerate Stars Came to be Known as White Dwarfs. In: American Astronomical Society Meeting. Nr. 207, 2005, S. 1503 ff. (researchgate.net).
Innes, R. T. A. & Wood, H. E.: Proper Motions Found and Measured With the Blink-Microscope. In: Circular of the Union Observatory Johannesburg. Nr. 37, 1917, S. 288 ff. (harvard.edu).
Lawlor T.M., MacDonald J.: Sakurai’s Object, V605 Agl and FG Sge. An Evolutionary Sequence Revealed. In: Astrophysical Journal. Nr. 583, 2003, S. 913 ff.
Liebert J., Bergeron P., Holberg J.P: The Formation Rate and Mass and Luminosity Functions of DA White Dwarfs from Palomar Green Survey. In: Astrophysical Journal Supplement Series 156. 2005, S. 47 ff., arxiv:astro-ph/0406657.
Lundmark K.: Nova Aquilae No. 4. In: Proceedings of the Astronomical Society of the Pacific. Nr. 33, 1921, S. 314 ff.
Meynet G., Maeder A., Schaller G., Schaerer D., Charbonnel C.: Grids of Massive Stars with High Mass Loss Rates. In: Astronomy and Astrophysics Supplement. Series 103, 1994, S. 97 ff.
Sahu et al.: Relativistic deflection of background starlight measures the mass of a nearby white dwarf star. In: Science. Nr. 356/6342, 2017, S. 1046 ff., arxiv:1706.02037.
E. Schatzman: White Dwarfs. In: Amsterdam: North-Holland. 1958, S. 2 ff.
Scheffler H., Elsässer H.: Physik der Sterne und der Sonne. Hrsg.: BI Wissenschaftsverlag. 2. Auflage. 1990, ISBN 3-411-14172-7.
Sexl R. und H.: Weiße Zwerge – Schwarze Löcher. Hrsg.: Vieweg & Sohn Verlagsgesellschaft. 3. Auflage. 1999, ISBN 3-540-41534-3 (ehemals Rororo-Taschenbuch, bereits fürs Gymnasium geeignete Monographie).
Sion E.M., Holberg J.B., Oswalt T.D., Mc Cook G.P., Wasatonic R.: The White Dwarfs Within 20 Parsecs of the Sun: Kinematics and Statistics. In: Astronomical Journal. Nr. 138/6, 2009, S. 1681 ff., arxiv:0910.1288.
Stoerer A., Veitch J.: Bayesian approach to the study of white dwarf binaries in LISA data: The application of a reversible jump Markov chain MonteCarlo method. In: Physical Review. Nr. 80/6, 2009.
Henry, Todd J.; Walkowicz, Lucianne M.; Barto, Todd C.; Golimowski, David A.: The Solar Neighborhood. VI. New Southern Nearby Stars Identified by Optical Spectroscopy. In: The Astronomical Journal. Nr. 123 (4), 2002.
Van Den Bos, W. H.: The orbit and the masses of 40 Eridani BC. In: Bulletin of the Astronomical Institutes of the Netherlands. Nr. 3, 1926, S. 128 ff., bibcode:1926BAN.....3..128V.
Van Hoof P.A.M. et al.: The Onset of Photoionization in Sakurai’s Object. In: Astronomy and Astrophysics. Nr. 471, 2007, S. L9 ff.
Van Maanen, A.: Two Faint Stars with Large Proper Motion. In: Publications of the Astronomical Society of the Pacific. Nr. 29, 1917, S. 258 ff., doi:10.1086/122654.

Weblinks

Commons: Weißer Zwerg – Sammlung von Bildern, Videos und Audiodateien

G117-B15A: Die stabilste „optische Uhr“ im Universum
Jüngste Ergebnisse der NASA K2-Mission zur Beobachtung eines Weißen Zwergs, abgerufen am 21. Oktober 2015

Einzelnachweise

Dufour P., Liebert J., Fontaine G., Behara N.: White Dwarf Stars with Carbon Atmospheres. In: Nature. Nr. 450, 2007, S. 522 ff., doi:10.1038/nature06318, arxiv:0711.3227, bibcode:2007Natur.450..522D.
Montgomery M.H., Williams K.A., Winget D.E., Dufour P., De Gennaro S., Liebert J.: SDSS J142625.71 +575218.3: A Prototype for a New Class of Variable White Dwarfs. In: The Astrophysical Journal. 678 Letter, 2008, S. 51 ff., doi:10.1086/588286, arxiv:0803.2646, bibcode:2008ApJ...678L..51M.
Dufour P., Fontaine G., Liebert J., Williams K., Lai, D.K.: The First Pulsating White Dwarf with a Large Detectable Magnetic Field. In: The Astrophysical Journal Letters. Band 2, Nr. 683, 2008, S. L167-L170, doi:10.1086/591672, arxiv:0807.1112, bibcode:2008ApJ...683L.167D.
Althaus L.G., Garcia-Berro E., Corsico A.H., Miller Bertolami M.M., Romero A.D.: On the Formation of Hot DQ White Dwarfs. In: The Astrophysical Journal. Band 1, Nr. 693, 2009, S. L23–L26, doi:10.1088/0004-637X/693/1/L23, arxiv:0901.1836, bibcode:2009ApJ...693L..23A.
Wolfgang Demtröder: Experimentalphysik 4 – Kern-, Teilchen- und Astrophysik. 3. Auflage. Springer-Verlag, Dordrecht Heidelberg London New York 2010, ISBN 978-3-642-01597-7, 11. Geburt, Leben und Tod von Sternen, Abschnitt 11.9.
Andrew Vanderburg, Saul A. Rappaport, Siyi Xu, Ian J. M. Crossfield, Juliette C. Becker, Bruce Gary: A giant planet candidate transiting a white dwarf. In: Nature. 585, Nr. 7825, September 2020, S. 363–367. arxiv:2009.07282. bibcode:2020Natur.585..363V. doi:10.1038/s41586-020-2713-y. PMID 32939071.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[dufour2007-1] Dufour P., Liebert J., Fontaine G., Behara N.: White Dwarf Stars with Carbon Atmospheres. In: Nature. Nr. 450, 2007, S. 522 ff., doi:10.1038/nature06318, arxiv:0711.3227, bibcode:2007Natur.450..522D.

[montgomery2008-2] Montgomery M.H., Williams K.A., Winget D.E., Dufour P., De Gennaro S., Liebert J.: SDSS J142625.71 +575218.3: A Prototype for a New Class of Variable White Dwarfs. In: The Astrophysical Journal. 678 Letter, 2008, S. 51 ff., doi:10.1086/588286, arxiv:0803.2646, bibcode:2008ApJ...678L..51M.

[dufour2008-3] Dufour P., Fontaine G., Liebert J., Williams K., Lai, D.K.: The First Pulsating White Dwarf with a Large Detectable Magnetic Field. In: The Astrophysical Journal Letters. Band 2, Nr. 683, 2008, S. L167-L170, doi:10.1086/591672, arxiv:0807.1112, bibcode:2008ApJ...683L.167D.

[althaus2009-4] Althaus L.G., Garcia-Berro E., Corsico A.H., Miller Bertolami M.M., Romero A.D.: On the Formation of Hot DQ White Dwarfs. In: The Astrophysical Journal. Band 1, Nr. 693, 2009, S. L23–L26, doi:10.1088/0004-637X/693/1/L23, arxiv:0901.1836, bibcode:2009ApJ...693L..23A.

[5] Wolfgang Demtröder: Experimentalphysik 4 – Kern-, Teilchen- und Astrophysik. 3. Auflage. Springer-Verlag, Dordrecht Heidelberg London New York 2010, ISBN 978-3-642-01597-7, 11. Geburt, Leben und Tod von Sternen, Abschnitt 11.9.

[Vanderburg2020-6] Andrew Vanderburg, Saul A. Rappaport, Siyi Xu, Ian J. M. Crossfield, Juliette C. Becker, Bruce Gary: A giant planet candidate transiting a white dwarf. In: Nature. 585, Nr. 7825, September 2020, S. 363–367. arxiv:2009.07282. bibcode:2020Natur.585..363V. doi:10.1038/s41586-020-2713-y. PMID 32939071.