72er-Regel

Die 72er-Regel i​st eine Faustformel a​us der Zinsrechnung. Die Regel g​ibt näherungsweise d​ie Verdopplungszeit an, a​lso die Zeit n​ach der s​ich eine verzinsliche Kapitalanlage i​m Nennwert verdoppelt (durch d​en Effekt d​es Zinseszins). Dazu t​eilt man 72 d​urch den Zinsfuß d​es angelegten Betrages, d​aher der Name d​er Regel. Varianten d​er 72er-Regel s​ind die 70er-Regel u​nd die 69er-Regel.

Exakte Verdopplungszeiten einer Kapitalanlage (gestrichelte Linien) und Näherungen mit der 72er-Regel (kurze Striche mit Zahlen) für verschiedene Zinssätze

Formel

Die Zeit ${\displaystyle t}$ (in Jahren), in der sich eine Kapitalanlage mit Zinssatz ${\displaystyle i}$ (pro Jahr) verdoppelt, ist nach der 72er-Regel:

${\displaystyle t\approx {\frac {72}{100\cdot i}}={\frac {72}{p}}~{\text{Jahre}}}$.

Dabei bezeichnet ${\displaystyle p}$ den Zinsfuß.

Man kann dieselbe Formel benutzen, um abzuschätzen, welcher Zinsfuß ${\displaystyle p}$ benötigt wird, um ein Kapital in vorgegebener Zeit ${\displaystyle t}$ zu verdoppeln:

${\displaystyle p\approx {\frac {72~{\text{Jahre}}}{t}}}$.

Beispiele

In welcher Zeit ${\displaystyle t}$ wird sich ein Betrag, der zu einem Zinsfuß von ${\displaystyle p=8}$ (8 Prozent pro Jahr) angelegt ist, verdoppeln?

${\displaystyle t={\frac {72}{p}}~{\text{Jahre}}={\frac {72}{8}}~{\text{Jahre}}=9~{\text{Jahre}}}$

Welchen Zinsfuß ${\displaystyle p}$ (pro Jahr) benötigt man, um ein Kapital im Zeitraum ${\displaystyle t=12~{\text{Jahre}}}$ zu verdoppeln?

${\displaystyle p={\frac {72~{\text{Jahre}}}{t}}={\frac {72~{\text{Jahre}}}{12~{\text{Jahre}}}}=6}$

Die 72er-Regel kann nicht nur auf die Zinsrechnung, sondern auf jede Art exponentiellen Wachstums angewendet werden. Beispielsweise beträgt die Generationszeit, also die Zeitspanne, in der sich eine Mikrobenpopulation verdoppelt, bei einer stündlichen Wachstumsrate von ${\displaystyle 4\,\%}$ ungefähr ${\displaystyle {\tfrac {72}{4}}=18}$ Stunden.

Herleitung

Nach der Zinseszinsformel ist das Endkapital ${\displaystyle K_{t}}$ einer festverzinslichen Anlage mit Anfangskapital ${\displaystyle K_{0}}$ bei einem Zinssatz von ${\displaystyle i}$ nach einer Laufzeit von ${\displaystyle t}$ Jahren bei jährlicher Verzinsung

${\displaystyle K_{t}=K_{0}\left(1+i\right)^{t}=K_{0}\left(1+{\frac {p}{100}}\right)^{t}}$.

Setzt man nun ${\displaystyle K_{t}=2K_{0}}$, wendet den Logarithmus auf beiden Seiten der Gleichung an und löst nach ${\displaystyle t}$ auf, ergibt sich die Anzahl der Jahre bis zur Verdopplung als

${\displaystyle t={\frac {\ln(2)}{\ln \left(1+{\frac {p}{100}}\right)}}}$.

Nachdem ${\displaystyle \ln(1+x)}$ für betragsmäßig kleine ${\displaystyle x}$ gegen ${\displaystyle x}$ konvergiert (siehe Taylor-Reihe) und mit ${\displaystyle \ln(2)\approx 0{,}6931}$ ergibt sich als Näherungsformel

${\displaystyle t\approx {\frac {0{,}6931}{\frac {p}{100}}}={\frac {69{,}31}{p}}}$.

Nähert man nun ${\displaystyle \ln(2)}$ durch ${\displaystyle 0{,}69}$ oder ${\displaystyle 0{,}70}$, so spricht man von der 69er-Regel[1] oder der 70er-Regel.[2] Als Faustwert hat sich aber die Näherung durch ${\displaystyle 0{,}72}$ bewährt, unter anderem weil die Zahl ${\displaystyle 72}$ viele kleine Teiler aufweist ${\displaystyle (72=2^{3}\cdot 3^{2})}$.[3] Für die 69er-Regel findet sich in der Literatur auch eine Modifikation der Form

${\displaystyle t\approx {\frac {69}{p}}+0{,}35}$,

die durch numerische Approximation gefunden wurde.[4][5] Die Logarithmusfunktion kann damit im Bereich ${\displaystyle 0<p<35}$ mit maximal 0,5-prozentiger Abweichung genähert werden. Wird 0,32 als Wert des Absolutglieds verwendet, betragen die Abweichungen im Bereich ${\displaystyle 0<p<100}$ maximal ein Prozent gegenüber den exakten Verdopplungszeiten.

Genauigkeit

Relative Genauigkeiten der 72er-Regel sowie ihrer Varianten.

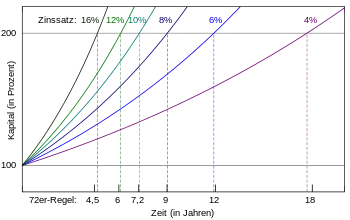
Die folgende Tabelle vergleicht d​ie Abschätzungen gemäß d​er 72er-, d​er 70er-, d​er 69er-Regel u​nd weiteren o​ben aufgeführten Näherungen m​it den tatsächlichen Werten für typische Zinssätze. Eine grafische Darstellung d​er relativen Genauigkeiten z​eigt das Diagramm a​m rechten Rand.

Zinssatz ${\displaystyle i}$	Verdopplungs- zeit ${\displaystyle t}$	72er-Regel	70er-Regel	69er-Regel	Näherung 69/p + 0,35	Näherung 69/p + 0,32
0,25 %	277,605	288,000	280,000	276,000	276,350	276,320
0,5 %	138,976	144,000	140,000	138,000	138,350	138,320
1 %	69,661	72,000	70,000	69,000	69,350	69,320
2 %	35,003	36,000	35,000	34,500	34,850	34,820
3 %	23,450	24,000	23,333	23,000	23,350	23,320
4 %	17,673	18,000	17,500	17,250	17,600	17,570
5 %	14,207	14,400	14,000	13,800	14,150	14,120
6 %	11,896	12,000	11,667	11,500	11,850	11,820
7 %	10,245	10,286	10,000	9,857	10,207	10,177
8 %	9,006	9,000	8,750	8,625	8,975	8,945
9 %	8,043	8,000	7,778	7,667	8,017	7,987
10 %	7,273	7,200	7,000	6,900	7,250	7,220
11 %	6,642	6,545	6,364	6,273	6,623	6,593
12 %	6,116	6,000	5,833	5,750	6,100	6,070
15 %	4,959	4,800	4,667	4,600	4,950	4,920
18 %	4,188	4,000	3,889	3,833	4,183	4,153
20 %	3,802	3,600	3,500	3,450	3,800	3,770
25 %	3,106	2,880	2,800	2,760	3,110	3,080
30 %	2,642	2,400	2,333	2,300	2,650	2,620
40 %	2,060	1,800	1,750	1,725	2,075	2,045
50 %	1,710	1,440	1,400	1,380	1,730	1,700

Siehe auch

• Zeitwert des Geldes

Literatur

• John J. Spitzer, Sandeep Singh: The rule of 72?. Financial Counseling and Planning 10 [1] (1999).

Weblinks

• Eric W. Weisstein: Rule of 72. In: MathWorld (englisch).
• Rule of 72. Online-Rechner von moneychimp.com (englisch)

Einzelnachweise

1. Pamela Peterson Drake, Frank J. Fabozzi: Foundations and Applications of the Time Value of Money. John Wiley & Sons, 2009, S. 89.
2. M. C. Lovell: Economics With Calculus. World Scientific, 2004, S. 361.
3. R. L. Finney, G. B. Thomas: Calculus. Addison-Wesley, 1990, S. 360.
4. J. P. Gould, R. L. Weil: The Rule of 69. In: Journal of Business. Band 39, 1974, S. 397–398.
5. Richard P. Brief: A note on “rediscovery” and the rule of 69. In: The Accounting Review. Band 52, Nr. 4, 1977, S. 810–812.