Sechseck
Ein Sechseck oder Hexagon [hɛksaˈgoːn] (von griech. ἑξα, héxa, „sechs“ und γωνία, gonía, „Winkel; Ecke“) ist ein Polygon (Vieleck), bestehend aus sechs Ecken und sechs Seiten. Sind alle sechs Seiten gleich lang, spricht man von einem gleichseitigen Sechseck. Sind darüber hinaus alle Winkel an den sechs Ecken gleich groß, dann wird das Sechseck regulär oder regelmäßig genannt.
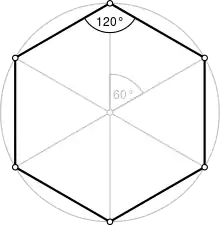
Mathematische Zusammenhänge
Die zugrundeliegenden Zusammenhänge des regulären Sechsecks beschrieb erstmals Euklid in seinem 15. mathematischen Satz des 4. Buchs Die Elemente. Werden die gegenüberliegenden Ecken des Sechsecks miteinander verbunden, ergeben sich sechs gleichseitige Dreiecke. Werden dagegen alle nicht gegenüberliegenden Ecken miteinander verbunden, so erhält man ein Hexagramm.
Formeln
| Mathematische Formeln zum regelmäßigen Sechseck | ||
|---|---|---|
| Flächeninhalt | 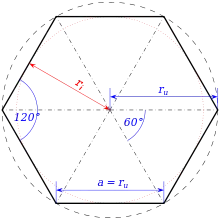 | |
| Länge der Diagonalen | ||
| Inkreisradius oder halbe Schlüsselweite |
||
| Umkreisradius | ||
| Innenwinkel | ||
Konstruktion bei gegebenem Umkreis
Ein reguläres Sechseck lässt sich als Konstruktion mit Zirkel und Lineal sehr einfach aus einem Kreis darstellen, indem der Radius des Kreises sechsmal auf dem Kreisrand abgetragen wird (siehe Konstruktion 1). Die erhaltenen Punkte sind die Ecken des Sechsecks. Alternativ genügt nach Euklid[1] das zweimalige Abtragen auf dem Kreisrand. Die fehlenden Ecken können dann über die Geraden durch den Mittelpunkt des Umkreises und die bereits bekannten Ecken konstruiert werden (siehe Konstruktion 2 nach Euklid, als animierte Grafik).
 Konstruktion 1
Konstruktion 1 Konstruktion 2 nach Euklid, als animierte Grafik
Konstruktion 2 nach Euklid, als animierte Grafik

Konstruktion bei gegebener Seitenlänge
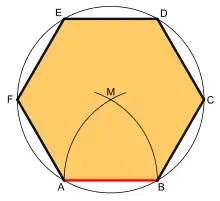
Ein reguläres Sechseck lässt sich ebenfalls konstruieren, wenn eine vorhandene Strecke als Seitenlänge verwendet werden soll.
- Bezeichne die Endpunkte der Strecke mit A bzw. B.
- Zeichne einen Kreisbogen um den Punkt A mit dem Radius AB.
- Zeichne einen Kreisbogen um den Punkt B mit dem Radius AB, es ergibt sich der Schnittpunkt M, der Mittelpunkt vom späteren Umkreis.
- Zeichne einen Kreis um den Punkt M mit dem Radius AM, dies ist der Umkreis des späteren Sechsecks.
- Trage die Strecke AB ab dem Punkt B viermal mit dem Zirkel auf dem Umkreis ab.
- Verbinde die benachbarten Eckpunkte miteinander, somit ergibt sich das Sechseck ABCDEF.
Näherungsweise Konstruktion
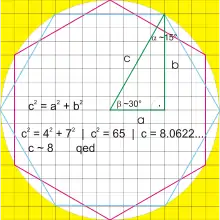
Eine für praktische Zwecke oft ausreichende Annäherung an ein reguläres Sechseck erhält man, wenn man das Hexagon aus annähernd gleichseitigen Dreiecken konstruiert, welche ein Verhältnis Höhe zu Grundseite von 7:8 haben. Diese Annäherung findet dort Anwendung, wo ein Fehler von knapp 1 % toleriert werden kann. So können zum Beispiel Karten oder Spielfelder in leicht zu zeichnende und leicht zu berechnende Sektoren eingeteilt werden.
Die Punkte Pi (x|y) sind im Folgenden nach den Ziffern einer Uhr nummeriert, das Zentrum ist (0|0):
- Koordinaten eines liegenden Sechsecks
- P1 (4|7), P3 (8|0), P5 (4|−7), P7 (−4|−7), P9 (−8|0), P11 (−4|7)
- Koordinaten eines auf der Spitze stehenden Sechsecks
- P2 (7|4), P4 (7|−4), P6 (0|−8), P8 (−7|−4), P10 (−7|4), P12 (0|8)
Eine bessere Annäherung erhält man, wenn man bei den obigen Koordinaten die Zahlen 4, 7 und 8 durch 15, 26 bzw. 30 ersetzt. Weitere mögliche Tripel sind (56, 97, 112) oder (209, 362, 418). Bei allen diesen Tripeln weichen die aus den entsprechenden Seitenlängen gebildeten Dreiecke nur sehr wenig von einem rechtwinkligen Dreieck mit den spitzen Winkeln 30° und 60° ab. Weitere solche Dreiecke findet man iterativ, indem man aus den „Katheten“ und (mit ) eines schon bekannten solchen Dreiecks die neuen Katheten bildet. Die „Hypotenuse“ ist wegen der 30°-Eigenschaft stets das Doppelte der kurzen Kathete.
Sechseckige Parkettierungen

Das reguläre Sechseck ist neben dem gleichseitigen Dreieck und der Raute (mit dem Quadrat als Spezialfall) das einzige gleichseitige Polygon, mit dem eine Ebene lückenlos parkettiert werden kann. Anders als bei der Parkettierung mit Dreiecken oder Rauten hat das einzelne Polygon in einer hexagonalen Parkettierung nur Nachbarn, die über vollständige Kanten verbunden sind, aber keine, die nur über Ecken oder Kantenteile verbunden sind. Der Abstand der Mittelpunkte zweier direkt benachbarter Sechsecke beträgt
Die Möglichkeit zur Bildung sechseckiger Parkettierungen ist eine Ursache dafür, dass Sechsecke deutlich häufiger sind als regelmäßige Fünfecke, Siebenecke und als die höheren Polygone.
 3-6-3-6
3-6-3-6 3-3-3-3-6 (zwei gespiegelte Varianten)
3-3-3-3-6 (zwei gespiegelte Varianten) 3-4-6-4
3-4-6-4 4-6-12
4-6-12
Die Zahlen unter den Abbildungen geben an, wie viele Ecken die regelmäßigen Polygone haben, die jeweils an einem Punkt zusammenstoßen. Die Innenwinkel ergeben zusammen 360°.
Polyeder mit regelmäßigen Sechsecken
Einige Polyeder haben regelmäßige Sechsecke als Seitenflächen, zum Beispiel der Tetraederstumpf, der Oktaederstumpf, das Große Rhombenkuboktaeder, der Ikosaederstumpf und das Große Rhombenikosidodekaeder. Die genannten Polyeder sind archimedische Körper.
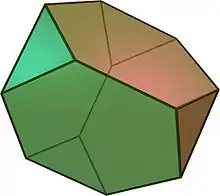 Tetraederstumpf
Tetraederstumpf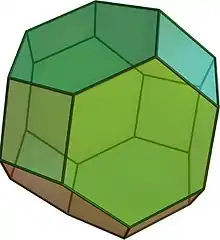 Oktaederstumpf
Oktaederstumpf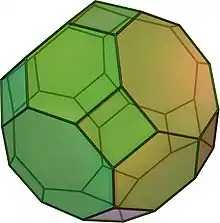 Großes Rhombenkuboktaeder
Großes Rhombenkuboktaeder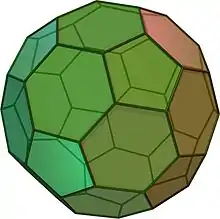 Ikosaederstumpf (Fußballkörper)
Ikosaederstumpf (Fußballkörper)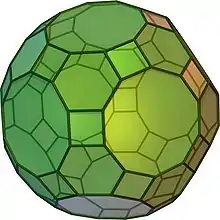 Großes Rhombenikosidodekaeder
Großes Rhombenikosidodekaeder
Vorkommen von Sechsecken und hexagonalen Strukturen
Regelmäßige Sechsecke sind in Kunst, Kultur, Natur und Technik häufig anzutreffen. Die folgende Liste zeigt nur einige Beispiele.
Natur


- Bienenwabe: Die hexagonale Form der Wände ergibt ein optimales Verhältnis von Wandmaterial zu Volumen und bietet hohe Stabilität. Es ist im Grunde wie eine Aneinanderreihung der Kreisform mit dessen Vorteilen, ohne jedoch ungenutzte Zwischenräume zu hinterlassen.
- Aufgrund der Elektronenorbitale bilden kovalente Bindungen eines Moleküls oft den 120° Winkel zueinander, die in einem gleichseitigen Sechsecks vorliegen, wodurch sechseckige Molekülformen besonders stabil sind und hexagonale Ringe bzw. Molekülformen oft auftreten.
- Kristallstrukturen: Viele Kristalle bilden hexagonale Formen aus. Bekannte Beispiele sind natürliches (Wasser-)Eis und sechsstrahlige Schneeflocken, da beim Wassermolekül die Wasserstoffatome ebenfalls annähernd einen 120° Winkel zum Sauerstoff bilden.
- In der Kristallstruktur vom Graphit bildet Kohlenstoff planare Flächen aus Sechsecken. Weitere elementare Formen vom Kohlenstoff – Graphen, Fullerene und Kohlenstoffnanoröhren – bestehen ebenfalls aus, ggf. leicht gekrümmten, Sechsringen.
- Eine bedeutende Grundstruktur von organischen Molekülen ist der (aromatische) Benzolring, der ein regelmäßiges Sechseck mit Kohlenstoffatomen als Eckpunkte bildet. Im Gegensatz zu einem aliphatischen Kohlenwasserstoffring wie Cyclohexan bildet Benzol sogar räumlich betrachtet ein ebenes Sechseck.
- Basalt bildet, wenn es langsam erstarrt, oft meterlange sechseckige Säulen.
- Bei der Suprafluidität von Flüssigkeiten: Anordnung von quantisierten mechanischen Wirbeln
- Der Nordpol des Planeten Saturn ist der Mittelpunkt einer stabilen atmosphärischen Struktur in der Form eines nahezu regelmäßigen Sechsecks. Es hat einen Durchmesser von fast 25.000 Kilometern.
- Die Konvektionszellen beim Bénard-Experiment können sich als reguläre Sechsecke ausbilden.
- Die Ortszellen im Hippocampus, die die Position eines Tieres in der räumlichen Umgebung codieren, lassen sich als Eckpunkte von Sechsecken[2] darstellen.
- Das Wintersechseck ist ein Sternbild, das zufällig von der Erde aus gesehen ein unregelmäßiges Sechseck bildet.
Kunst und Kultur


In der Architektur, Malerei und Grafik des Judentums und des Christentums liegt bei der Verwendung des Hexagons die Symbolik der Zahl 6 zugrunde, deren Bedeutung sich aus der Summe der ersten drei Zahlen (1+2+3) und deren Zahlensymbolik ergibt. Sie und damit das gleichseitige Hexagon symbolisieren in beiden Religionen die Allmacht Gottes. Sie stehen aber auch für Gleichgewicht und Harmonie des Göttlichen und Weltlichen, die zudem in der Gleichseitigkeit des Hexagons sowie in dessen Zusammensetzung aus sechs gedachten oder geometrisch sichtbaren gleichseitigen Dreiecken liegen, also auch die Symbolik der Zahl 3 enthalten. Die Zahl 6 und das Hexagon können, je nach Zusammenhang, auch Symbol des Sechstagewerks der Schöpfung (1. Buch Mose) sein.
Ein Beispiel aus der christlichen Malerei des Spätmittelalters ist der hexagonale Tisch im „Paradiesgärtlein“ des Oberrheinischen Meisters (um 1410; Frankfurt, Städelsches Kunstinstitut): Er beherrscht farblich leuchtend in Form und Symbolkraft des Sechsecks das Bild und ist entscheidender Faktor zum Verständnis des Bildes, der auch durch seine Rolle in der Bildkomposition betont wird.
Weitere Beispiele der Verwendung des Hexagons, jedoch nur eingeschränkt von symbolischer Bedeutung:
- Architektur: In vielen Kulturen ist das Hexagon ein grundlegendes Element zur Gestaltung von Fenstern, Fliesen und Mosaiken. Beispiele sind Fresken am Dom zu Pisa oder Mauerelemente mancher Gebäude in Pompeji; ebenso befindet sich die Glastonbury Abbey innerhalb eines (gedachten) Hexagons. Bei der Privatvilla Kentuck Knob von Architekt Frank Lloyd Wright ist das Sechseck das durchgehende Konstruktionsprinzip, der Lantern Tower in Schottland erhebt sich über einem sechseckigen Grundriss, ebenso der Musentempel im Schlosspark Tiefurt in Thüringen wie der Wasserturm Zörbig in Sachsen-Anhalt. Mehrere Sechsecke bilden den Grundriss des Düsseldorfer Rank-Xerox-Hauses.
- M. C. Escher: Viele seiner Mosaik-Variationen basieren auf Sechsecken.
- Frankreich: Aufgrund seiner ungefähr sechseckigen Form wird das auf dem europäischen Festland gelegene Territorium Frankreichs auch als l'hexagone bezeichnet. Daher befindet sich auf der Rückseite der französischen 1- und 2-Euro-Münzen ein stilisierter Baum in einem Hexagon, und der Marschall von Frankreich trägt seine sieben Sterne auf den Schulterstücken im Sechseck angeordnet.
- Musikelektronik: Die ersten kommerziellen elektronischen Schlagzeuge der britischen Firma Simmons waren hexagonal geformt.
Technik

- Die Köpfe von Schrauben sind häufig sechseckig, entweder als Außensechskant oder als Innensechskant (Inbus). Auch Sechskantmuttern sind verbreitet.
- Eine Sandwichplatte mit Wabenkern, also eine Verbundkonstruktion mit einem wabenförmigen Stützkern, wird bei Konstruktionen eingesetzt, bei denen es auf eine hohe Festigkeit bei geringem Gewicht oder Materialverbrauch ankommt.
- Stützstrukturen vieler 3D-Drucker, die auf dem Verfahren Fused Deposition Modeling basieren, können bei vielen Modellen unter anderem als Wabenstruktur gedruckt werden, welche ähnlich der vorher genannten Sandwichbauweise eine hohe Stabilität mit geringem Gewicht und Filamentverbrauch kombiniert.
Spiele
Bei vielen Spielen, besonders bei Konfliktsimulationsspielen, besteht der Spielplan aus einem Sechseckraster. Dadurch können unter anderem Entfernungen zwischen zwei Feldern einfacher bestimmt werden als bei einem Quadratraster (zum Beispiel einem Schachbrett). Als besonders prominent gilt hier das Spiel Die Siedler von Catan, bei dem sowohl das Spielbrett selbst als auch die einzelnen Landschaftsplättchen die Sechseckform aufweisen.
Siehe auch
Weblinks
Anmerkungen und Einzelnachweise
- Johann Friedrich Lorenz: Euklids Elemente, fünfzehn Bücher. Hrsg.: Im Verlag der Buchhandlung des Waysenhauses. Halle 1781, S. 65 ff. (Euklids Elemente, Viertes Buch, Der 15. Satz., In einen gegebnen Cirkel, A B C D E F, ein gleichseitiges und gleichwinkliches Hexagon zu beschreiben. [abgerufen am 17. Juni 2017]).
- Dr. Christian Wolf: Gesucht und gefunden: Orientierungszellen 2014 siehe Seltsames Muster und Mentales Koordinatensystem. Abgerufen am 17. Juni 2017.