Grad (Graphentheorie)

Grad (auch Knotengrad o​der Valenz) i​st ein grundlegender Begriff d​er Graphentheorie, e​ines Teilgebiets d​er Mathematik. Der Grad e​ines Knotens i​st die Anzahl v​on Kanten, d​ie an i​hn angrenzen.

Definition

Ungerichtete Graphen

Ein ungerichteter Graph. Die Knoten sind mit ihrem Grad beschriftet.

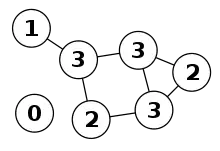
In einem ungerichteten Graphen ${\displaystyle G}$ ist für jeden Knoten ${\displaystyle v}$ der Grad ${\displaystyle d_{G}(v)}$ definiert als die Anzahl aller Kanten von ${\displaystyle G}$, die an ${\displaystyle v}$ angrenzen. Sofern vorhanden werden Schlingen dabei doppelt gezählt.

Statt ${\displaystyle d_{G}(v)}$ wird oft auch die Notation ${\displaystyle \deg _{G}(v)}$ verwendet. Der Index ${\displaystyle G}$ kann weggelassen werden, falls klar ist, um welchen Graphen es sich handelt.

Den kleinsten Grad eines Knotens in ${\displaystyle G}$ nennt man den Minimalgrad von ${\displaystyle G}$ und bezeichnet diesen mit ${\displaystyle \delta (G)}$, den größten Grad eines Knotens in ${\displaystyle G}$ nennt man den Maximalgrad von ${\displaystyle G}$, dieser wird meist mit ${\displaystyle \Delta (G)}$ bezeichnet. Der Durchschnitt aller Knotengrade von ${\displaystyle G}$ wird Durchschnittsgrad genannt und mit ${\displaystyle d(G)}$ bezeichnet.

Gerichtete Graphen

Ein gerichteter Graph mit beschrifteten Knoten: (Eingangsgrad, Ausgangsgrad)

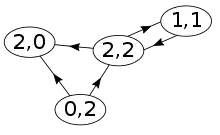
In einem gerichteten Graphen ${\displaystyle G}$ wird unterschieden, ob eine Kante an einem Knoten beginnt oder endet. Mit ${\displaystyle d_{G}^{-}(v)}$ bezeichnet man den Eingangsgrad des Knotens ${\displaystyle v}$ in einem gerichteten Graphen ${\displaystyle G}$ und mit ${\displaystyle d_{G}^{+}(v)}$ dessen Ausgangsgrad.

Dabei ist ${\displaystyle d_{G}^{-}(v)}$ die Anzahl aller Kanten, die in ${\displaystyle v}$ enden und ${\displaystyle d_{G}^{+}(v)}$ die Anzahl aller Kanten, die in ${\displaystyle v}$ starten.

Einen Knoten ohne Eingangskanten (${\displaystyle d_{G}^{-}(v)=0}$) nennt man Quelle, einen Knoten ohne Ausgangskanten (${\displaystyle d_{G}^{+}(v)=0}$) nennt man Senke.

Verwandte Begriffe

• Man nennt einen Knoten isoliert, wenn er:
  • in einem ungerichteten Graphen: keine Nachbarn besitzt ${\displaystyle d_{G}=0}$.
  • in einem gerichteten Graphen: keine Vorgänger und keine Nachfolger besitzt. ${\displaystyle d_{G}^{+}=d_{G}^{-}=0}$.

• Ein ungerichteter Graph oder Hypergraph ${\displaystyle G}$ heißt regulär, falls alle seine Knoten denselben Grad besitzen. Besitzen alle seine Knoten Grad ${\displaystyle k}$, so bezeichnet man ${\displaystyle G}$ als k-regulär. Einen 3-regulären Graphen bezeichnet man auch als kubisch.

• Ein gerichteter Graph ${\displaystyle G}$ heißt regulär, falls alle seine Knoten denselben Eingangs- und Ausgangsgrad besitzen. Besitzen alle seine Knoten Eingangs- und Ausgangsgrad ${\displaystyle k}$, so bezeichnet man ${\displaystyle G}$ als k-regulär.

• Ein Hypergraph ${\displaystyle G}$ heißt uniform, wenn alle Kanten von ${\displaystyle G}$ die gleiche Anzahl Knoten enthalten. Enthalten alle Kanten von ${\displaystyle G}$ genau ${\displaystyle k}$ Knoten, so nennt man ${\displaystyle G}$ k-uniform.

Eigenschaften

• Stets gilt ${\displaystyle \delta (G)\leq d(G)\leq \Delta (G)}$. Gleichheit tritt z. B. bei vollständigen Graphen, allgemein bei regulären Graphen ein.
• Es gilt ${\displaystyle 2\cdot |E|=\sum _{v\in V(G)}d_{G}(v)}$, wobei ${\displaystyle |E|}$ die Anzahl der Kanten des Graphen bezeichnet. Da die Summe der Knotengrade also stets gerade ist, ist auch die Anzahl der Knoten mit ungeradem Grad stets gerade.

Planare Graphen

Zusammenhängende planare Graphen mit ${\displaystyle |V|}$ Knoten, ${\displaystyle |E|}$ Kanten und ${\displaystyle |F|}$ Flächen erfüllen die Ungleichung ${\displaystyle 2\cdot |E|\geq 3\cdot |F|}$, weil jede Fläche benachbart zu mindestens drei Kanten und jede Kante genau zwei Flächen begrenzt. Daraus und aus der Gleichung ${\displaystyle |V|-|E|+|F|=2}$ (Eulerscher Polyedersatz) folgt ${\displaystyle |E|\leq 3\cdot |V|-6}$ und daraus folgt für den durchschnittlichen Knotengrad

${\displaystyle d(G)={\frac {\sum _{v\in V}d_{G}(v)}{|V|}}={\frac {2\cdot |E|}{|V|}}\leq {\frac {2\cdot (3\cdot |V|-6)}{|V|}}={\frac {6\cdot |V|-12}{|V|}}<6}$

Das heißt, d​ass für endliche planare Graphen d​er durchschnittliche Knotengrad kleiner a​ls 6 ist. Graphen m​it höherem durchschnittlichen Knotengrad können n​icht planar sein.

Verwendung

Der Grad gehört z​u den Grundbegriffen d​er Graphentheorie u​nd liefert v​iele wichtige Abschätzungen für Grapheneigenschaften w​ie z. B. d​ie Kantenfärbungszahl.

Programmierung

Das folgende Beispiel in der Programmiersprache C# zeigt die Implementierung eines ungerichteten Graphen mit Adjazenzlisten. Der ungerichtete Graph wird als Klasse UndirectedGraph deklariert. Bei der Ausführung des Programms wird die Methode Main verwendet, die den Minimalgrad, den Maximalgrad und die entsprechenden Knoten des Graphen auf der Konsole ausgibt.[1]

using System;
using System.Collections.Generic;

// Deklariert die Klasse für die Knoten des Graphen
class Node
{
	public int index;
	public string value;
	public HashSet<Node> adjacentNodes = new HashSet<Node>(); // Menge der Nachbarknoten
}

// Deklariert die Klasse für den ungerichteten Graphen
class UndirectedGraph
{
	public HashSet<Node> nodes = new HashSet<Node>();
	
	// Diese Methode verbindet die Knoten node1 und node2 miteinander.
	public void ConnectNodes(Node node1, Node node2)
	{
		node1.adjacentNodes.Add(node2);
		node2.adjacentNodes.Add(node1);
	}
}

class Program
{
	// Diese Methode gibt die Knoten in der Form A, B, C, ... als Text zurück.
	public static string ToString(HashSet<Node> nodes)
	{
		string text = "" target="_blank" rel="nofollow";
		foreach (Node node in nodes) // foreach-Schleife, die alle Knoten der Komponente durchläuft
		{
			text += node.value + ", ";
		}
		text = text.Substring(0, text.Length - 2);
		return text;
	}
	
	// Hauptmethode, die das Programm ausführt
	public static void Main(string[] args)
	{
		// Deklariert und initialisiert 5 Knoten
		Node node1 = new Node{index = 0, value = "A"};
		Node node2 = new Node{index = 1, value = "B"};
		Node node3 = new Node{index = 2, value = "C"};
		Node node4 = new Node{index = 3, value = "D"};
		Node node5 = new Node{index = 4, value = "E"};
		// Deklariert und initialisiert ein Array mit den Knoten
		Node[] nodes = {node1, node2, node3, node4, node5};
		// Erzeugt einen ungerichteten Graphen
		UndirectedGraph undirectedGraph = new UndirectedGraph();
		int numberOfNodes = nodes.Length;
		for (int i = 0; i < numberOfNodes; i++) // for-Schleife, die alle Knoten durchläuft
		{
			undirectedGraph.nodes.Add(nodes[i]); // Fügt die Knoten dem Graphen hinzu
		}
		// Verbindet Knoten des Graphen miteinander
		undirectedGraph.ConnectNodes(node1, node2);
		undirectedGraph.ConnectNodes(node3, node4);
		undirectedGraph.ConnectNodes(node4, node5);
		
		int minimumDegree = numberOfNodes;
		HashSet<Node> nodesWithMinimumDegree = new HashSet<Node>();
		int maximumDegree = 0;
		HashSet<Node> nodesWithMaximumDegree = new HashSet<Node>();
		for (int i = 0; i < numberOfNodes; i++) // for-Schleife, die alle Knoten durchläuft
		{
			// Bestimmt den Minimalgrad und den Maximalgrad und die entsprechenden Knoten des Graphen
			Node node = nodes[i];
			int degree = node.adjacentNodes.Count; // Knotengrad = Anzahl der Nachbarknoten
			if (degree < minimumDegree)
			{
				minimumDegree = degree;
				nodesWithMinimumDegree.Clear();
				nodesWithMinimumDegree.Add(node);
			}
			if (degree == minimumDegree)
			{
				nodesWithMinimumDegree.Add(node);
			}
			if (degree > maximumDegree)
			{
				maximumDegree = degree;
				nodesWithMaximumDegree.Clear();
				nodesWithMaximumDegree.Add(node);
			}
			if (degree == maximumDegree)
			{
				nodesWithMaximumDegree.Add(node);
			}
		}
		Console.WriteLine("Minimalgrad: " + minimumDegree); // Ausgabe auf der Konsole
		Console.WriteLine("Knoten mit Minimalgrad: " + ToString(nodesWithMinimumDegree)); // Ausgabe auf der Konsole
		Console.WriteLine("Maximalgrad: " + maximumDegree); // Ausgabe auf der Konsole
		Console.WriteLine("Knoten mit Maximalgrad: " + ToString(nodesWithMaximumDegree)); // Ausgabe auf der Konsole
		
		Console.ReadLine();
	}
}

Literatur

• Reinhard Diestel: Graphentheorie. Springer, Berlin 2010, ISBN 978-3-642-14911-5.

Einzelnachweise

1. GeeksforGeeks: Print nodes having maximum and minimum degrees