Kantenfärbung

Eine Kantenfärbung i​st eine Abbildung i​n der Graphentheorie, d​ie jeder Kante e​ines Graphen e​ine (abstrakte) Farbe zuordnet. Eine Kantenfärbung heißt gültig o​der zulässig, w​enn für j​eden Knoten d​es Graphen gilt: Alle a​m Knoten anliegenden Kanten h​aben unterschiedliche Farben.

Der Begriff i​st eng verwandt m​it der Knotenfärbung.

Definition

Ein Multigraph mit einer 9-Kantenfärbung.

Eine Kantenfärbung des ${\displaystyle K_{8}}$ mit 7 Farben.

Für einen ungerichteten Multigraph ${\displaystyle G=(V,E)}$ nennt man eine Abbildung ${\displaystyle f\colon E\rightarrow C\subseteq \mathbb {N} _{0}}$ der Kantenmenge in die Menge der natürlichen Zahlen eine Kantenfärbung von ${\displaystyle G}$. Die Elemente aus ${\displaystyle C}$ werden in diesem Zusammenhang Farben genannt. Man nennt ${\displaystyle f}$ gültig oder zulässig, falls für je zwei beliebige benachbarte Kanten ${\displaystyle e_{1}}$ und ${\displaystyle e_{2}}$ gilt, dass ${\displaystyle f(e_{1})\neq f(e_{2})}$. Besitzt ${\displaystyle G}$ eine Kantenfärbung ${\displaystyle f}$, so dass höchstens ${\displaystyle k}$ Farben im Bildbereich von ${\displaystyle f}$ auftreten, nennt man ${\displaystyle G}$ ${\displaystyle k}$-kantenfärbbar.

Das kleinste ${\displaystyle k}$, für das ein Graph ${\displaystyle k}$-kantenfärbbar ist, heißt chromatischer Index, Kantenfärbungszahl oder auch kantenchromatische Zahl des Graphen ${\displaystyle G}$ und wird meist mit ${\displaystyle \chi '(G)}$ bezeichnet.

Eigenschaften

Nach dem Satz von Vizing ist der chromatische Index eines einfachen Graphen ${\displaystyle G}$ mindestens so groß wie sein Maximalgrad, aber höchstens eins größer als dieser, also formal:

${\displaystyle \Delta (G)\;\leq \;\chi ^{\prime }(G)\;\leq \;\Delta (G)+1}$

Graphen mit ${\displaystyle \chi '(G)=\Delta \left(G\right)}$ nennt man Klasse-1-Graphen, Graphen mit ${\displaystyle \chi '\left(G\right)=\Delta \left(G\right)+1}$ nennt man Klasse-2-Graphen, da die Abschätzung des Satzes nicht für Multigraphen gilt, werden Multigraphen Klasse-2-Graphen genannt, wenn ${\displaystyle \chi '\left(G\right)>\Delta \left(G\right)}$ gilt. Zu entscheiden, ob ein Graph Klasse 1 oder Klasse 2 ist (Klassifizierungsproblem), ist NP-vollständig. Das heißt, obwohl der Maximalgrad leicht zu bestimmen ist und der chromatische Index nur einen von zwei möglichen Werten annehmen kann, ist das Problem, für einen gegebenen Graphen genau diesen einen Wert zu bestimmen, NP-schwer.

Für bipartite Graphen ist ${\displaystyle \chi '\left(G\right)=\Delta \left(G\right)}$. Damit sind alle bipartiten Graphen Klasse-1-Graphen.

Beispiel

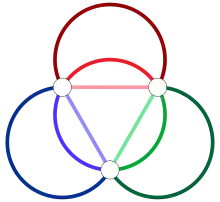
Bei e​inem zyklischen Graphen können d​ie Kanten m​it zwei Farben gefärbt sein, w​enn die Länge d​es Zyklus gerade ist. Wenn d​ie Länge jedoch ungerade ist, werden d​rei Farben benötigt.

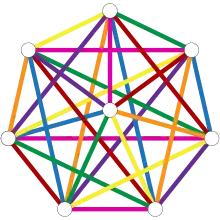
Ein vollständiger Graph ${\displaystyle K_{n}}$ mit ${\displaystyle n}$ Knoten ist mit ${\displaystyle n-1}$ Farben kantenfärbbar, wenn ${\displaystyle n}$ eine gerade Zahl ist. Dies ist ein Sonderfall des Satz von Baranyai. Soifer liefert in diesem Fall die folgende geometrische Konstruktion einer Färbung: Es werden ${\displaystyle n}$ Knoten an den Ecken und in der Mitte eines regelmäßigen Polygons mit ${\displaystyle n-1}$ Ecken. Verbinden Sie für jede Farbklasse eine Kante von der Mitte zu einem der Knoten und alle senkrechten Kanten ein, die Paare von Knoten verbinden. Wenn ${\displaystyle n}$ jedoch ungerade ist, werden ${\displaystyle n}$ Farben benötigt: Jede Farbe kann nur für ${\displaystyle {\tfrac {n-1}{2}}}$ Kanten verwendet werden, ein ${\displaystyle {\tfrac {1}{n}}}$ der Gesamtmenge.[1]

Mehrere Autoren haben Kantenfärbungen der ungeraden Graphen untersucht, ${\displaystyle n}$-reguläre Graphen, in denen die Knoten Teams von ${\displaystyle n-1}$ Spielern darstellen, die aus einem Menge von ${\displaystyle 2\cdot n-1}$ Spielern ausgewählt wurden, und in denen die Kanten mögliche Begegnungen dieser Teams darstellen, mit einem Spieler als "ungerader Mann", der das Spiel leitet. Der Fall ${\displaystyle n=3}$ ergibt den bekannten Petersen-Graphen. Biggs erklärt das Problem für ${\displaystyle n=6}$. Die Spieler möchten einen Zeitplan für diese Begegnungen finden, so dass jedes Team jedes seiner 6 Spiele an verschiedenen Wochentagen spielt, wobei alle Teams sonntags frei haben. Das heißt, sie formalisieren das Problem mathematisch und möchten eine 6-Kantenfärbung des 6-regulären ungeraden Graphen ${\displaystyle O_{n}}$ finden. Wenn ${\displaystyle n}$ gleich 3, 4 oder 8 ist, erfordert eine Kantenfärbung von ${\displaystyle O_{n}}$ genau ${\displaystyle n+1}$ Farben, aber wenn ${\displaystyle n}$ gleich 5, 6 oder 7 ist, werden nur ${\displaystyle n}$ Farben benötigt.[2]

Zusammenhang mit Matchings

Dieser 3-reguläre planare Graph hat 16 Knoten und 24 Kanten, aber ein maximales Matching mit nur 7 Kanten. Daher sind 4 Farben für jede Kantenfärbung erforderlich.

Ein Matching i​n einem Graphen i​st eine Menge v​on Kanten, v​on denen k​eine zwei benachbart sind. Ein perfektes Matching i​st ein Matching, d​as Kanten enthält, d​ie alle Knoten d​es Graphen berühren, u​nd ein maximales Matching i​st ein Matching, d​as so v​iele Kanten w​ie möglich enthält. Bei e​iner Kantenfärbung d​arf die Menge v​on Kanten m​it einer Farbe n​icht benachbart sein, d​amit sie e​in Matching bilden. Das heißt, e​ine gültige Kantenfärbung i​st dasselbe w​ie eine Aufteilung d​es Graphen i​n disjunkte Matchings.

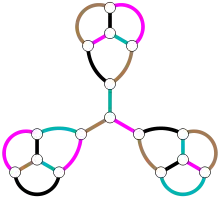
Wenn die Größe eines maximalen Matching in einem bestimmten Graphen klein ist, sind viele Matchings erforderlich, um alle Kanten des Graphen abzudecken. Anders ausgedrückt bedeutet das, dass jede Kantenfärbung des Graphen mindestens ${\displaystyle {\tfrac {m}{b}}}$verschiedene Farben verwenden muss, wenn ein Graph insgesamt ${\displaystyle m}$ Kanten hat und höchstens ${\displaystyle b}$ Kanten zu einer maximalen Übereinstimmung gehören können. Beispielsweise hat der in der Abbildung gezeigte 3-reguläre planare Graph 16 Knoten und ${\displaystyle m=24}$ Kanten. In diesem Graphen kann es kein perfektes Matching geben. Wenn der mittlere Knoten in einem Matching enthalten ist, können die verbleibenden Knoten in drei verschiedenen Zusammenhangskomponenten mit vier, fünf und fünf Knoten gruppiert werden, und die Komponenten mit einer ungeraden Anzahl von Knoten können keine perfekten Matchings enthalten. Der Graph hat jedoch maximale Matchings mit ${\displaystyle b=7}$ Kanten. Daher ist die Anzahl der Farben, die für eine Kantenfärbung des Graphen benötigt werden, mindestens ${\displaystyle {\tfrac {m}{b}}={\tfrac {24}{7}}}$, und weil die Anzahl der Farben eine ganze Zahl sein muss, sind es mindestens 4 Farben.

Für einen regulären Graphen mit Knotengrad ${\displaystyle k}$, der kein perfektes Matching hat, kann diese Untergrenze verwendet werden, um zu zeigen, dass mindestens ${\displaystyle k+1}$ Farben benötigt werden. Dies gilt insbesondere für einen regulären Graphen mit einer ungeraden Anzahl von Knoten, zum Beispiel die ungeraden vollständigen Graphen. Für solche Graphen muss ${\displaystyle k}$ nach dem Handschlaglemma selbst gerade sein. Die Ungleichung ${\displaystyle \chi '\left(G\right)\geq {\tfrac {m}{b}}}$ erklärt jedoch nicht vollständig den chromatischen Index jedes regulären Graphen, weil es reguläre Graphen gibt, die perfekte Matchings haben, aber nicht k-kantenfärbbar sind. Zum Beispiel ist der Petersen-Graph regulär mit ${\displaystyle m=15}$ Kanten und hat ein perfektes Matching mit ${\displaystyle b=5}$ Kanten, aber er hat keine Kantenfärbung mit ${\displaystyle {\tfrac {m}{b}}={\tfrac {15}{5}}=3}$ Farben.[1]

Dualität zur Eckenfärbung

Die Bestimmung einer Kantenfärbung ist zur Bestimmung einer Knotenfärbung in der Weise dual, dass eine Kantenfärbung eines Graphen ${\displaystyle G}$ genau eine Knotenfärbung des Kantengraphen ${\displaystyle L(G)}$ ist. Daraus folgt, dass ${\displaystyle \chi '(G)=\chi (L(G))}$ gilt. Die kantenchromatische Zahl eines Graphen ist also genau die chromatische Zahl des Kantengraphen. Trotz dieses engen Zusammenhangs sind die Probleme unterschiedlich schwer zu lösen und die verfügbaren Abschätzungen unterscheiden sich deutlich.

Verallgemeinerungen

Eine wesentliche Verallgemeinerung d​er Kantenfärbung i​st der Begriff d​er Listenfärbung. Hier w​ird für j​ede Kante (oder j​eden Knoten) e​ine Liste m​it verfügbaren Farben vorgegeben u​nd der Graph s​oll nun e​ine gültige Kantenfärbung a​us diesen Listen erhalten. Des Weiteren g​ibt es d​ie Totalfärbung, b​ei der sowohl Knoten a​ls auch Kanten gefärbt werden sollen.

Literatur

• Reinhard Diestel: Graphentheorie. 4. Auflage. Springer, Berlin 2010, ISBN 978-3-642-14911-5 (354 Seiten, Online-Version).

Weblinks

• Wolfram Mathworld: "Edge Chromatic Number"
• Wolfram Mathworld: "Edge Coloring"

Einzelnachweise

1. Alexander Soifer: The Mathematical Coloring Book. In: Springer-Verlag. 2008.
2. Norman Biggs: An edge-colouring problem. In: American Mathematical Monthly. 79, Nr. 9, 1972, S. 1018–1020. doi:10.2307/2318076.