Kuboktaeder
Das Kuboktaeder (auch Kubooktaeder oder Kubo-Oktaeder) ist ein Polyeder (Vielflächner) mit 14 Seiten (6 Quadrate und 8 regelmäßige Dreiecke), 12 gleichartigen Ecken und 24 gleich langen Kanten.
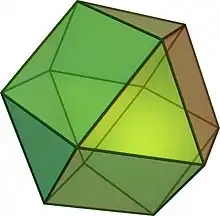

Aufgrund seiner Regelmäßigkeit zählt das Kuboktaeder zu den 13 archimedischen Körpern. Neben dem Ikosidodekaeder ist es der einzige konvexe quasireguläre Körper. Der Umkugelradius (Abstand der Ecken zum Mittelpunkt) ist wie beim Antikuboktaeder gleich der Kantenlänge.
Sein Dualkörper ist das Rhombendodekaeder.
Mathematische Eigenschaften
Symmetrie
Mit 12 Ecken, 14 Flächen und 24 Kanten wird der eulersche Polyedersatz erfüllt:
Hinsichtlich seiner symmetrischen Eigenschaften lässt sich das Kuboktaeder als flächenquasiregulärer konvexer Polyeder einordnen:[1]
- Alle Flächen sind regulär. Da das Kuboktaeder über Quadrate und Dreiecke verfügt, sind die Flächen aber nicht homogen, weshalb es auch keine Inkugel hat. Diese Bedingung wird nur von den Platonischen und den Catalanischen Körpern erfüllt.
- Alle Kanten sind symmetrieäquivalent, da sich an jeder Kante genau ein Quadrat und ein Dreieck berühren. Abgesehen vom Ikosidodekaeder erfüllt kein anderer Archimedischer Körper diese Bedingung. Das Kuboktaeder besitzt eine Kantenkugel.
- Alle Ecken sind symmetrieäquivalent, da an jeder Ecke jeweils zwei Dreiecke und zwei Quadrate aufeinandertreffen. Daher verfügt das Kuboktaeder über eine Umkugel.
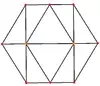
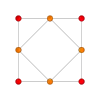
Orthogonale Projektion
Für das Kuboktaeder existieren spezielle orthogonale Projektionen, in denen primär seine Ecken, seine Kanten, seine Dreiecke oder seine Quadrate erkennbar sind.
| Ecken | Kanten | Dreiecke | Quadrate |
 |
 |
 |
 |
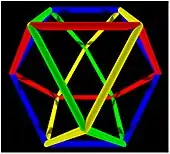
Das Kuboktaeder kann entlang sechs zusammenhängender Kanten geschnitten werden. Die entstehende Schnittfläche ist ein regelmäßiges Sechseck. Insgesamt sind vier solcher Schnitte möglich. Die Schnittflächen sind keine Symmetrieebenen des Kuboktaeders, sondern Fixebenen von Drehspiegelsymmetrien (siehe Bild rechts).[2]
Kugelpackung

Sechs eng um eine Ursprungskugel herum angeordnete Kugeln können mit ihren Mittelpunkten in sechs in einer Ebene befindlichen Ecken eines Kuboktaeders liegen. Über und unter diesem Sechseck hat das Kuboktaeder je drei weitere Ecken, die mit den Mittelpunkten von je drei zusätzlichen die Ursprungskugel berührenden Kugeln zusammenfallen. Das Kuboktaeder ist somit Koordinationspolyeder der kubisch dichtesten Kugelpackung.[3] Dies gilt ebenso für das nicht reguläre Antikuboktaeder, bei dem sich die sechs oben und unten angelegten Kugeln vertikal übereinander befinden und nicht versetzt wie beim Kuboktaeder.
Formeln
| Größen eines Kuboktaeders mit Kantenlänge a | |
|---|---|
| Volumen | |
| Oberflächeninhalt | |
| Umkugelradius | |
| Kantenkugelradius | |
| Flächenwinkel (Quadrat–Trigon) ≈ 125° 15′ 52″ |
|
| 3D-Kantenwinkel = 120° |
|
| Eckenraumwinkel ≈ 0,7837 π |
|
| Sphärizität ≈ 0,905 |
|
Geometrische Verwandtschaft
Würfel und Oktaeder
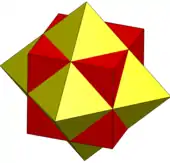
Das Kuboktaeder lässt sich als Ableitung zweier Platonischer Körper ansehen: Durchdringen sich ein Würfel (Kubus) und ein Oktaeder, entsteht als Schnittmenge (Kern) ein Kuboktaeder.[4] Sein Name ist als Kofferwort von diesen beiden Körpern abgeleitet. Auch die alte Bezeichnung Mittelkristall bezieht sich auf seine Rolle als Zwischenform.[5] Die Flächen eines Würfels (sechs Quadrate) und eines Oktaeders (acht Dreiecke) bilden die insgesamt 14 Flächen des Kuboktaeders.
Durch Abstumpfung der Ecken lässt sich ein Kuboktaeder jeweils aus beiden Grundkörpern erzeugen: Stumpft man die Ecken eines Würfels bis zum Mittelpunkt seiner Kanten ab, verkleinern sich einerseits seine sechs Quadrate; andererseits bilden sich an den bisherigen Ecken acht Dreiecke. Durch Abstumpfung der Ecken eines Oktaeders bis zur Kantenmitte werden seine acht Dreiecke stark verkleinert und die bisherigen Ecken zu sechs Quadraten.
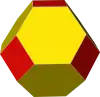
Bei der Erzeugung eines Kuboktaeders durch Abstumpfung von Würfel oder Oktaeder entstehen zwei Zwischenformen: Werden beide Grundkörper nicht bis zur Kantenmitte, sondern nur teilweise abgestumpft, lassen sich die beiden Archimedischen Körper Hexaederstumpf beziehungsweise Oktaederstumpf erschaffen.
 |
 |
 |
 |
 |
| Würfel | Hexaederstumpf | Kuboktaeder | Oktaederstumpf | Oktaeder |
| → Abstumpfung → | ← Abstumpfung ← | |||
Tetraeder

Auch aus einem weiteren Platonischen Körper lässt sich das Kuboktaeder ableiten: Wird ein Tetraeder entlang seiner sechs Kanten ausgedehnt, entstehen sechs Vierecke. An den bisherigen Ecken des Tetraeders bilden sich vier Dreiecke, zusätzlich zu den vier ursprünglich bestehenden. Führt man diesen Prozess weiter, bis die Vierecke quadratisch sind, erhält man ein Kuboktaeder. Alternativ kann dieser Vorgang als Abstumpfung der Kanten eines Tetraeders gedacht werden.
 |
 |
| Tetraeder | Kuboktaeder |
| → Ausdehnung → | |
Ikosaeder

Das Kuboktaeder ist auch selbst eine Ausgangsform für die Ableitung anderer Polyeder. Alle Platonischen und Archimedischen Körper lassen sich entweder aus Kuboktaeder, Ikosidodekaeder oder Tetratetraeder (Oktaeder) durch Verdrehung (Torsion) ableiten. Bei diesen drei Polyedern handelt es sich um die möglichen Durchdringungskörper der Platonischen Körper.
Durch Verdrehung eines Kuboktaeders lässt sich mit dem Ikosaeder ein Platonischer Körper herstellen:[6] Die Dreiecke des Kuboktaeders bleiben dabei unverändert. Durch eine Verzerrung der Quadrate entstehen sechs Rhomben. Diese werden durch neue Kanten geteilt, so dass insgesamt zwölf regelmäßige Dreiecke entstehen, zusätzlich zu den ursprünglichen acht des Kuboktaeders. Der neue Körper hat somit 20 Dreiecke und ist ein Ikosaeder.
 |
 |
| Kuboktaeder | Ikosaeder |
| → Verdrehung → | |
Großes Rhombenkuboktaeder
Das Große Rhombenkuboktaeder, einer der Archimedischen Körper, wird auch als Kuboktaederstumpf bezeichnet. Tatsächlich lässt es sich aber nicht durch Abstumpfen aus einem Kuboktaeder herstellen,[7] wie der Name suggeriert. Dass es nicht so ist, lässt sich an der Art der an den Ecken des Kuboktaeders zusammenstoßenden Flächen erkennen: Auf den Dreiecken bilden je zwei von einer Ecke ausgehende Kanten einen Winkel von 60°, aber auf den Quadraten sind es 90°. Durch Abstumpfen würde jede Ecke zu einem Rechteck anstatt zu einem Quadrat werden, denn die Hypotenuse in einem gleichschenkligen Dreieck ist unter einem 90°-Gegenwinkel länger als unter einem 60°-Gegenwinkel.
Gleichwohl ist dieses abgestumpfte Kuboktaeder topologisch gleichwertig zum Kuboktaederstumpf, da es dieselbe Anzahl Flächen, Kanten und Ecken aufweist.
 |
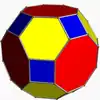 |
| Kuboktaeder | Kuboktaederstumpf |
Rhombendodekaeder
Der zum Kuboktaeder duale Körper ist das Rhombendodekaeder. Dieses weist 12 Flächen und 14 Ecken auf, also das umgekehrte Verhältnis wie beim Kuboktaeder. Wie bei allen Archimedischen Körpern ist der Dualkörper ein Catalanischer Körper. Während das Kuboktaeder die Schnittmenge bei der Durchdringung von Würfel und Oktaeder bildet, ist das Rhombendodekaeder dazu der Hüllkörper.
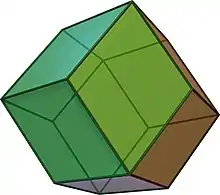 |
| Rhombendodekaeder |
Stellare Kuboktaeder
Es existieren vier verschiedene Sternformen zum Kuboktaeder. Der erste stellare Körper ist dabei identisch mit der Durchdringung von Würfel und Oktaeder.
 |
 |
 |
 |
 |
| Kuboktaeder | Erster Stern | Zweiter Stern | Dritter Stern | Vierter Stern |
| → Erweiterung → | ||||
Nicht-konvexe Polyeder
Zwei nicht-konvexe Körper teilen sich die Position der Kanten und Ecken mit dem Kuboktaeder: Beim Kubohemioktaeder bestehen nur die Quadrate, beim Oktahemioktaeder nur die Dreiecke. Die übrigen Flächen werden durch die vier Sechsecke innerhalb des Kuboktaeder eingenommen.[8] Das Kuboktaeder ist die konvexe Hülle der beiden anderen Körper.[9]
 |
 |
 |
| Kubohemioktaeder | Kuboktaeder | Oktahemioktaeder |
| ← Entflächung → | ||
Johnsonkörper
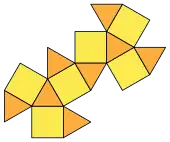
Wird ein Kuboktaeder entlang eines seiner Sechsecke durchschnitten, entstehen zwei Dreieckskuppeln, der Johnson-Körper J3.[4] Alternativ kann man sich das Kuboktaeder auch aus sechs Quadratpyramiden (J1) und acht Tetraedern zusammengesetzt vorstellen.
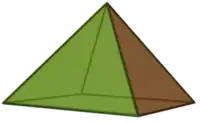 |
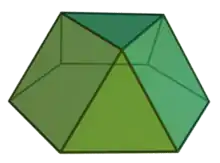 |
| Quadratpyramide | Dreieckskuppel |
Geschichte
Als einziger der Archimedischen Körper soll das Kuboktaeder schon Platon bekannt gewesen sein.[10]
Bezug zur physischen Welt
Chemie

Die kristalline Struktur synthetischer Diamanten basiert idealerweise auf dem Würfel oder dem Oktaeder – meist aber auf dem Kuboktaeder.[11] Oft sind diese Körper nicht regelmäßig, sondern nur Annäherungsformen. Natürliche Diamanten weisen meist eine oktaedrische kristalline Struktur auf.[12] Das Kuboktaeder ist der Kristall des Minerals Argentit (Ag2S).[13]
Jitterbug-Transformation

In Buckminster Fullers sogenannter Jitterbug-Transformation ist das Kuboktaeder mit 24 Kanten das ausgedehnteste Stadium, in dem die sechs Quadrate nur virtuell existieren. Durch Verdrehen entsteht ein Ikosaeder, wobei zwölf seiner 20 Dreiecke und sechs seiner 30 Kanten nur virtuell existieren. Nach weiterem Verdrehen stoßen die realen Kanten der realen acht Dreiecke paarweise zusammen, wodurch sich ein Oktaeder ergibt. Durch ein nochmaliges Verdrehen entsteht ein Tetraeder, wobei je vier Kanten zusammengefallen sind.[14] Dieser lässt sich schließlich in ein ebenes Dreieck zusammenklappen, bei dem je acht Kanten zusammenfallen.[15][16] Auf der Forschungsausstellung Heureka in Zürich 1991 wurde am begehbaren Heureka-Polyeder diese Transformation gezeigt. Während der Veränderung wurden die Besucher im Inneren auf einer Hebebühne synchron mit auf- und abbewegt.
 |
 |
 |
| Kuboktaeder | Ikosaeder | Oktaeder |
| → → Verdrehung → → | ||
Kunst
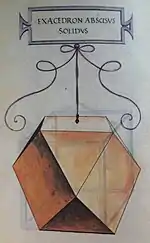
Leonardo da Vinci fertigte für Luca Paciolis De divina proportione (1509) Zeichnungen mehrerer Polyeder an, darunter auch des Kuboktaeders.
In M. C. Eschers Holzstich Sterne (1948) erscheint unten links ein kleines Kuboktaeder neben zahlreichen anderen Polyedern.
Spiel
Der Spielball des Tipp-Kick-Spiels ist ein Kuboktaeder.
Siehe auch
Weblinks
- Eric W. Weisstein: Kuboktaeder. In: MathWorld (englisch).
- Claus Michael Ringel: Kuboktaeder. Universität Bielefeld
- Kuboktaeder. Mathematische Basteleien
Einzelnachweise
- Renatus Ziegler: Platonische Körper. Dornach 2008, S. 94 f.
- Hans Walser: Steckmodelle. In: Der Mathematikunterricht. Band 55 (2009), S. 40.
- Ulrich Müller: Anorganische Strukturchemie (= Teubner Studienbücher Chemie). 3., überarbeitete und erweiterte Auflage. B. G. Teubner, Stuttgart 1996, ISBN 3-322-91187-X, S. 181 (eingeschränkte Vorschau in der Google-Buchsuche).
- Kuboktaeder auf Mathematische Basteleien
- Meyers Großes Konversations-Lexikon (1908)
- Ueli Wittorf: Einfache und doppelte Torsionspolyeder. In: Renatus Ziegler: Platonische Körper. Dornach 2008, S. 32–45.
- Johannes Kepler: Weltharmonik. München 1939 (Ausgabe in deutscher Übersetzung), S. 82 (eingeschränkte Vorschau in der Google-Buchsuche).
- Claus Michael Ringel über das Oktahemioktaeder
- MathWorld zum Oktahemioktaeder
- A. R. Rajwade: Convex Polyhedra with Regularity Conditions and Hilbert’s Third Problem. New Delhi 2001, S. 40.
- Amanda S. Barnard: The diamond formula: diamond synthesis – a gemmological perspective. Woburn 2000, S. 67 ff.
- Kristalline Struktur von Diamanten auf 1-Cultured-Diamonds
- Hugo Steinhaus: Mathematical Snapshots. Oxford 1950, S. 203.
- Demonstration der Jitterbug-Transformation zwischen Oktaeder und Kuboktaeder Buckminster Fuller’s Jitterbug. YouTube
- Demonstration der Jitterbug-Transformation zwischen Dreieck und Kuboktaeder Fuller Jitterbug Geometry – Jain Mathemagics. YouTube
- Die beiden letzten Schritte sind mit Hilfe eines Modells mit endlich dicken Dreiecks-Platten nicht darstellbar.