Kongruenz (Geometrie)
In der Geometrie sind zwei Figuren kongruent (deckungsgleich oder gleichförmig) (von lat. congruens = übereinstimmend, passend), wenn sie durch eine Kongruenzabbildung ineinander überführt werden können. Kongruenzabbildungen (auch Bewegungen genannt) sind Parallelverschiebung, Drehung, Spiegelung und die Verknüpfungen dieser Abbildungen.
Die Kongruenz von zwei ebenen geometrischen Figuren lässt sich anschaulich so deuten: Man kann die eine Figur mit der Schere ausschneiden und so auf die andere legen, dass beide genau übereinander liegen, einander also exakt „überdecken“ (→ vergleiche Kongruenzabbildung). Man nennt kongruente ebene Figuren daher auch deckungsgleich. Figuren, die nicht kongruent sind, werden auch inkongruent genannt.
Bei kongruenten ebenen Vielecken und räumlichen Polyedern müssen alle entsprechenden Streckenlängen und Winkelgrößen übereinstimmen.
In der absoluten Geometrie heißen zwei Figuren kongruent, wenn eine Bewegung des Punktraumes existiert, durch die die eine Figur bijektiv auf die andere abgebildet wird: kongruente Figuren unterscheiden sich nur durch die Lage, haben aber die gleiche Form und Größe.[1]
Vergleichsoperator
Ein weit verbreitetes Zeichen, die Kongruenz auszudrücken ist ≅, ein Gleichheitszeichen mit darüber liegender Tilde. Es entspricht dem Zeichen für »ungefähr gleich«: Unicode U+2245, HTML ≅, im Textsatzsystem LaTeX-math-Modus \cong.
Beispiel
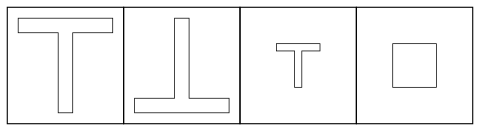
Die ersten beiden Figuren sind kongruent. Die dritte hat zwar die gleiche Form, ist aber kleiner. Sie ist daher ähnlich der ersten und zweiten Figur, aber nicht kongruent. Die letzte Figur hat nicht die gleiche Form und ist somit weder ähnlich noch kongruent zu den T-förmigen Figuren.
Kongruenz von Dreiecken
Besonders leicht lässt sich die Kongruenz von Dreiecken mithilfe folgender fünf Kongruenzsätze überprüfen, die einfache Kriterien liefern, unter denen zwei Dreiecke kongruent sind:
Stimmen zwei ebene Dreiecke in
- sss: drei Seitenlängen oder
- sws: zwei Seitenlängen und dem Maß des eingeschlossenen Winkels oder
- Ssw: zwei Seitenlängen und dem Maß des Winkels, der der längeren Seite gegenüberliegt oder
- wsw: einer Seitenlänge und den Maßen der beiden anliegenden Winkel oder
- wws: einer Seitenlänge, dem Maß eines anliegenden und dem des gegenüberliegenden Winkels[K 1]
überein, dann stimmen sie auch in den anderen Seitenlängen bzw. Winkelmaßen überein und sind damit kongruent.
Die Maximalzahl unabhängiger Bestimmungsstücke (Größen, die die Kongruenz bestimmen) ist beim ebenen Dreieck drei. Nicht nur Seitenlänge oder Winkelmaß können Bestimmungsstücke sein, sondern auch Inkreisradius, Umkreisradius, Höhe, Länge einer Seitenhalbierenden, Fläche etc.
Kongruenz von n-Ecken
Zur kongruenten Festlegung eines ebenen Polygons werden für jede zusätzliche Ecke zwei zusätzliche Bestimmungsstücke benötigt. Somit ist die Maximalzahl an unabhängigen Bestimmungsstücken für das -Eck .
Kongruenz in der Raumgeometrie
In der Stereometrie (Raum-Geometrie) spricht man bei Polyedern gegebenenfalls auch von der Kongruenz von Ecken, falls zwei Ecken dieselbe Anzahl von Kanten und Flächen mit den gleichen Winkeln (in derselben Reihenfolge) vereinigen; dabei müssen nicht nur die Winkel in den Seitenflächen des Polyeders gleich sein, sondern auch alle Winkel zwischen entsprechenden Kantenpaaren. Die eine Ecke muss sich ggf. durch eine Kongruenzabbildung in die andere überführen lassen.
Kommentare
- Da im ebenen Dreieck wegen der Winkelsumme von 180° mit zwei Winkeln auch der dritte gegeben ist, ist wws eine direkte Folge von wsw.
- Gerhard König: Grundwissen Mathematik SII Begriffswörterbuch. Ernst Klett Verlag, Stuttgart 1978, S. 126.