Raute

Eine Raute oder ein Rhombus (von altgriechisch ῥόμβος rhómbos)[1] ist in der Geometrie ein ebenes Viereck mit vier gleich langen Seiten. Gegenüberliegende Seiten sind parallel und gegenüberliegende Winkel gleich groß.

Rautendekor am Giebel des Südquerhauses der Kirche St Étienne in Beauvais, Picardie

Eigenschaften einer Raute:
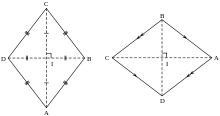
Jeweils zwei Seiten sind zueinander parallel und die Verbindungslinien der gegenüberliegenden Ecken schneiden einander im rechten Winkel

Etymologie

Das Etymologische Wörterbuch der deutschen Sprache sieht eine Verwendung des geometrischen Begriffs „Raute“ (mittelhochdeutsch rūte von althochdeutsch rūta, entlehnt von lateinisch ruta) seit dem 14. Jahrhundert und nennt die Entstehung „dunkel“. Den Auflagen von 1934 bis 1975 zufolge ergebe sich ein Rhombus, wenn die Spitzen der vier Kronblätter der Rautenblüte durch Geraden verbunden würden. Die Erstverwendung in der Geometrie sei für 1539 bezeugt. Spätere Auflagen enthalten diese Erklärung nicht mehr und führen nur eine fachsprachlich gleichbedeutende spätmittelhochdeutsche Form rūta an.[2] Botanische etymologische Lexika weisen darauf hin, dass die Weinraute keine rhombische Laubblattspreite habe.[3] Dem Etymologischen Wörterbuch von Wolfgang Pfeifer zufolge entstand der Begriff durch die „zuerst in der Heraldik auftretende geometrische Figur in der stilisierten vierteiligen Blütenform der Pflanze“ als Entlehnung aus lateinisch rūta, griechisch rhȳtḗ (ῥυτή) („Bitterkraut“).[4]

Doppelkreuz, Rhombus und Stern auf einer Rechenmaschine

Bezeichnungen und Darstellungen

→ Hauptartikel: Raute (Heraldik) und Raute (Symbol)

Neben „Raute“ werden die Ausdrücke „Rhombus“ (Plural: Rhomben) und „Karo“ verwendet. Beispielsweise heißt ein Webmuster bei Textilien: „Karomuster“.

Ein Quadrat, das auf der Spitze steht, wird manchmal ebenfalls verallgemeinernd als Raute bezeichnet.

Rautenformen als Schriftzeichen finden sich in Unicode im Block Geometrische Formen, beispielsweise ◆ (U+25C6 black diamond „vollflächiges Karo“), ◇ (U+25C7 white diamond „hohles Karo“) und ◊ (U+25CA lozenge „Rhombus“).

In der Heraldik heißen rautenförmige Elemente auch Wecke und Spindel, das auf die Spitze gestellte Quadrat auch Kantenwürfel.

Eigenschaften

Eine Raute ist ein ebenes Viereck mit vier gleich langen Seiten.[5] Alternativ lässt sich die Raute als Parallelogramm definieren, dessen Diagonalen einander rechtwinklig schneiden (siehe orthodiagonales Viereck).

Für jede Raute gilt:

• Gegenüberliegende Seiten sind parallel.
• Gegenüberliegende Innenwinkel sind gleich groß, benachbarte Innenwinkel supplementär, d. h., ihre Summe ist 180°.
• Die Innenwinkel werden durch eine Diagonale halbiert.
• Die beiden Diagonalen stehen senkrecht aufeinander und halbieren einander.
• Sie besitzt einen Inkreis und ist daher ein Tangentenviereck. Inkreismittelpunkt ist der Schnittpunkt der Diagonalen.
• Die Diagonalen sind Symmetrieachsen. Die beiden Symmetrieachsen stehen also senkrecht aufeinander.
• Sie ist punktsymmetrisch (zweizählig symmetrisch) bezüglich des Schnittpunkts der Diagonalen.
• Die Symmetriegruppe ist die Kleinsche Vierergruppe.

Die Raute kann charakterisiert werden als

• Parallelogramm mit zwei benachbarten gleich langen Seiten
• Parallelogramm mit orthogonalen Diagonalen
• Parallelogramm mit einer Diagonalen, die einen Innenwinkel halbiert
• Drachenviereck mit paarweise parallelen Seiten
• Viereck mit orthogonalen Diagonalen, die einander halbieren
• Viereck mit genau 2 Symmetrieachsen, von denen jede durch zwei gegenüberliegende Eckpunkte verläuft[6]
• Viereck, dessen zwei Diagonalen jeweils zwei gegenüberliegende Innenwinkel halbieren

Um eine Raute zu konstruieren, sind zwei Bestimmungsstücke, z. B. die Seitenlänge und ein Winkel, notwendig.

Formeln

Mathematische Formeln zur Raute
Flächeninhalt	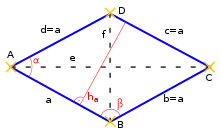${\displaystyle A=a\cdot h_{a}}$
	${\displaystyle A={\frac {e\cdot f}{2}}}$
	${\displaystyle A=a^{2}\cdot \sin(\alpha )=a^{2}\cdot \sin(\beta )}$
	${\displaystyle A={\frac {h_{a}^{2}}{\sin(\alpha )}}={\frac {h_{a}^{2}}{\sin(\beta )}}}$
Umfang	${\displaystyle u=4\cdot a}$
Seitenlänge	${\displaystyle a={\frac {1}{2}}\cdot {\sqrt {e^{2}+f^{2}}}}$
Länge der Diagonalen	${\displaystyle e=2\cdot a\cdot \cos \left({\frac {\alpha }{2}}\right)=2\cdot a\cdot \sin \left({\frac {\beta }{2}}\right)}$
	${\displaystyle f=2\cdot a\cdot \sin \left({\frac {\alpha }{2}}\right)=2\cdot a\cdot \cos \left({\frac {\beta }{2}}\right)}$
Inkreisradius	${\displaystyle r_{i}={\frac {h_{a}}{2}}={\frac {a\cdot \sin(\alpha )}{2}}={\frac {a\cdot \sin(\beta )}{2}}}$
Höhe	${\displaystyle h_{a}=a\cdot \sin(\alpha )=a\cdot \sin(\beta )}$
	${\displaystyle h_{a}={\frac {e\cdot f}{\sqrt {e^{2}+f^{2}}}}}$
Innenwinkel	${\displaystyle \alpha +\beta =180^{\circ }}$

Rautendekor am Giebel des Südquerhauses der St Julien, Chauriat, Auvergne

Optimierungsprobleme und das Quadrat

Es gibt verschiedene Optimierungsprobleme für Rauten. Sucht man eine Raute, die bei

• gegebener Länge der Höhe oder gegebenem Flächeninhalt des Inkreises den minimalen Umfang
• gegebener Länge der Höhe oder gegebenem Flächeninhalt des Inkreises den minimalen Flächeninhalt
• gegebenem Umfang die maximale Höhe oder den maximalen Flächeninhalt des Inkreises
• gegebenem Umfang den maximalen Flächeninhalt
• gegebenem Flächeninhalt die maximale Höhe oder den maximalen Flächeninhalt des Inkreises
• gegebenem Flächeninhalt den minimalen Umfang

hat, dann ergibt sich als Lösung jeweils das Quadrat.

Jeweils zwei der sechs Optimierungsprobleme sind im Prinzip dieselbe Fragestellung mit anderen gegebenen Größen, sodass es eigentlich nur drei verschiedene Optimierungsprobleme sind. Für die genannten Optimierungsprobleme ist das Quadrat die gesuchte Raute. Das gilt selbstverständlich nicht für alle Optimierungsprobleme.

Dass die Optimierungsprobleme für die Höhe und den Flächeninhalt des Inkreises jeweils dieselbe Lösung haben, ist offensichtlich, weil der Flächeninhalt ${\displaystyle \pi \cdot r_{i}^{2}={\tfrac {1}{4}}\cdot \pi \cdot h_{a}^{2}}$ des Inkreises eine stetige und streng monoton steigende Funktion mit der Funktionsvariablen ${\displaystyle h_{a}}$ ist.

Ist zum Beispiel bei gegebener Höhe ${\displaystyle h_{a}}$ die Raute mit dem kleinsten Flächeninhalt gesucht, dann kann man den Flächeninhalt mit Ungleichungen abschätzen.

Eine Raute mit den Diagonalenlängen ${\displaystyle e}$ und ${\displaystyle f}$ hat die Höhe ${\displaystyle {\frac {e\cdot f}{\sqrt {e^{2}+f^{2}}}}}$ und den Flächeninhalt ${\displaystyle {\frac {e\cdot f}{2}}}$. Das Quadrat mit der Seitenlänge ${\displaystyle {\frac {e\cdot f}{\sqrt {e^{2}+f^{2}}}}}$ hat dieselbe Höhe und den Flächeninhalt ${\displaystyle {\frac {e^{2}\cdot f^{2}}{e^{2}+f^{2}}}}$. Wegen der Ungleichung vom arithmetischen und geometrischen Mittel ${\displaystyle {\sqrt {e\cdot f}}\leq {\frac {e+f}{2}}}$ gilt ${\displaystyle {\frac {e^{2}\cdot f^{2}}{e^{2}+f^{2}}}\leq {\frac {e\cdot f}{2}}}$ für alle positiven Diagonalenlängen ${\displaystyle e}$ und ${\displaystyle f}$ und Gleichheit genau dann, wenn ${\displaystyle e=f}$ ist. Daraus folgt, dass das Quadrat die Raute mit dem kleinsten Flächeninhalt ist.

Kombinationen mehrerer Rauten

Zum Stern („Rautenstern“) schließen sich nur Rauten, deren Zentriwinkel (also der Winkel in der Spitze, in der man sie aneinanderlegt) gleich ${\displaystyle 360^{\circ }/n}$ mit einer natürlichen Zahl ${\displaystyle n}$ ist. Sie bilden dann einen ${\displaystyle n}$-zackigen Stern. Das gilt nicht für den dreidimensionalen Fall, hierbei lassen sich auch anderswinklige Rauten in ihrer Spitze aneinanderfügen und ergeben dann pyramidenförmige Spitzen.

Parkettierungen mit Rauten

• Durch seine Definition eignet sich jede Raute für eine flächendeckende Parkettierung, aber nur in zwei Hauptrichtungen (siehe platonische Parkettierung). Hier bildet die Rautenparkettierung (mit ihrer Sonderform, dem Quadratgitter, also einem orthogonalen Raster) eine der 17 möglichen Symmetriegruppen der Parkettierungen.[7]
• Eine solche Kachelung (flächenfüllende, schiefwinklig-platonische Kachelung) findet sich auf der Staatsflagge Bayerns (Rautenflagge), heraldische Fachsprache: schräg gerautet.
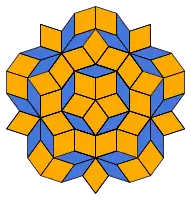
• Eine Besonderheit ist die aperiodische (quasikristalline) Penrose-Parkettierung zweier Rauten mit Innenwinkeln von 36° und 144° bzw. 72° und 108°.

• 
  Rautengitter-Parkettierung in der Staatsflagge Bayerns (Rautenflagge)
• 
  Alternierende Parkettierung mit Rauten
• 
  Duale Parkettierung einer archimedischen Parkettierung
• 
  Penrose-Parkettierung
• 
  Penrose-Parkettierung

Rhombendach der Marienkirche in Dortmund

Polyeder mit Rauten

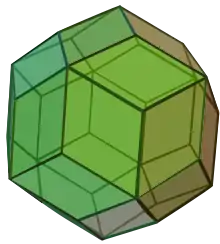
Einige Polyeder haben Rauten als Seitenflächen, zum Beispiel die Rhomboeder. Die Oberfläche von Rhombendodekaeder und Rhombentriakontaeder, zweier catalanischer Körper, besteht aus kongruenten Rauten. Rhomboeder, Rhombendodekaeder und Rhombentriakontaeder sind Polyeder, die ausschließlich von Rauten begrenzt sind. Die genannten Polyeder sind drehsymmetrisch, d. h., sie können durch Drehung um bestimmte Rotationsachsen auf sich selbst abgebildet werden.

• 
  Rhomboeder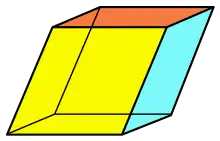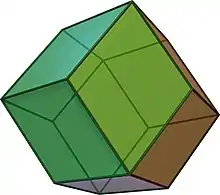
• 
  Rhombendodekaeder
• 
  Rhombentriakontaeder

Rauten in Architektur, Kunst und Design

Ein aus Kieselsteinen gelegtes Rautenmosaik in der altmakedonischen Hauptstadt Pella stammt aus alexandrinischer Zeit. Beliebt waren abstrahierte Rautenmuster als apotropäische Zeichen in der Kunst der Berber im Maghreb. In der europäischen Kunst sind sie dagegen nur selten anzutreffen, Beispiele finden sich etwa im Dekor der Südseite der Prioratskirche St-Julien in Chauriat oder im Giebel des Nordquerhauses der Kirche St Étienne in Beauvais.

• 
  Sechszackiger Rautenstern
• 
  Das Argyle-Muster wird manchmal als Rautenmuster bezeichnet
• 
  Logo von Renault (1972)
• 
  Skulptur von Victor Vasarely am Budapester Südbahnhof
• 
  Fußbodenmosaik aus Pella, Altmakedonien

Das Rhombendach ist ein Turmdach, das sich aus vier rautenförmigen Dachflächen zusammensetzt. Die Dachschrägen sind gegenüber den Giebelwänden um 45 Grad versetzt.

Die Rhombusleiste wird zur Verkleidung von Fassaden oder für Sichtschutzwände eingesetzt. Der Querschnitt bildet jedoch üblicherweise keine Raute, sondern ein Parallelogramm.

Weblinks

• Weiterführende Informationen, Berechnungsbeispiele und Abbildungen

Einzelnachweise

1. Wilhelm Pape, Max Sengebusch (Bearb.): Handwörterbuch der griechischen Sprache. 3. Auflage, 6. Abdruck. Vieweg & Sohn, Braunschweig 1914 (zeno.org [abgerufen am 5. September 2020]).
2. Raute. In: Friedrich Kluge: Etymologisches Wörterbuch der deutschen Sprache. 11. Auflage 1934, 21. Auflage 1975, 25. Auflage 2011.
3. Ruta. In: Helmut Genaust: Etymologische Handbuch der deutschen Pflanzennamen. 3. Auflage 1989. Im Anschluss Ruta graveolens L. In: Friedhelm Sauerhoff: Etymologisches Wörterbuch der deutschen Pflanzennamen. 2. Auflage. 2004.
4. Wolfgang Pfeifer: Etymologisches Wörterbuch des Deutschen. Online, abgerufen am 5. September 2020.
5. Gerhard Holland: Geometrie in der Sekundarstufe. Bibliographisches Institut&Brockhaus AG, Mannheim/Wien/Zürich 1988, ISBN 3-411-03178-6, S. 163.
6. Lambacher-Schweizer: Mathematik für Gymnasien 6, Stuttgart, Klett-Verlag, 2010, ISBN 978-3-12-734561-2, S. 83. Es gibt weitere Belege in der fachdidaktischen Literatur.
7. Bewiesen von Jewgraf S. Fedorow 1891, nach Ian Stewart: Fünfeckige Kacheln. In: Spektrum der Wissenschaft. Januar 2000, S. 106–108 (Abb. S. 108).