Rekursion

Als Rekursion (lateinisch recurrere ‚zurücklaufen‘) wird ein prinzipiell unendlicher Vorgang, der sich selbst als Teil enthält oder mithilfe von sich selbst definierbar ist, bezeichnet.[1] Üblicherweise sind rekursive Vorgänge relativ kurz beschreibbar bzw. können durch eine relativ kurze Anweisung ausgelöst werden.[2][3] Die bei Rekursion aufeinander folgenden Teilvorgänge oder die nacheinander erzeugten Objekte sind nicht unabhängig voneinander, sondern zwischen jedem Schrittpaar oder Objektpaar besteht eine besondere, die rekursive Beziehung.

Unendlichfache Spiegelung als Beispiel für Rekursion: Die Person sitzt mit vorgehaltenem Spiegel einem größeren Wandspiegel gegenüber. Das jeweils folgende Spiegelbild enthält sich selbst als Teil.

“Der Begriff [Rekursion] ist sehr umfassend”.[4] In der Natur handelt es sich um einen häufig beobachtbaren Vorgang (z. B. beim Pflanzenwachstum). In vielen Bereichen der Kultur wird er nachgebildet, so in den schönen Künsten, wo das Phänomen u. a. als Mise en abyme bezeichnet wird. In Mathematik und Informatik ist Rekursion ein gängiger Begriff.

Rekursion ist auch eine Problemlösungsstrategie. Komplexe Sachverhalte können oft mit rekursiv formulierten Regeln sehr elegant erfasst werden. Das Grundprinzip ist dabei dann das Zurückführen einer allgemeinen Aufgabe auf eine einfachere Aufgabe derselben Klasse. Das wird u. a. auch beim sogenannten rekursiven Programmieren genutzt: Um Rekursion entstehen zu lassen, muss eine Prozedur, Funktion oder Methode lediglich sich selbst aufrufen. Dieser Prozess läuft weiter, bis eine im Programm enthaltene Abbruchbedingung greift.

In der Mathematik wird das rekursive Formulieren mit Vorteil zur Erklärung von Funktionen angewendet (siehe Rekursive Definition).

Einführende Beispiele für Rekursion

Rekursive Grafiken

Pythagoras-Baum

„Sprießender“ Pythagoras-Baum

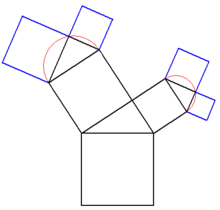
Rekursive Regeln können auch in der Erstellung von Grafiken verwendet werden, dies ergibt die sogenannten Fraktale – ästhetisch ansprechende, natürlich aussehende Gebilde. Ein Beispiel ist der Pythagoras-Baum. Er entsteht nach folgender Regel (der dritte Schritt zeigt die Rekursion):

Errichte auf einer gegebenen Grundlinie ein Quadrat.
Auf seiner Oberseite zeichne ein Dreieck mit vorgegebenen Winkeln bzw. Höhe.
Wende die beiden obigen Schritte jeweils erneut auf die beiden freien Seiten des neuentstandenen Dreieckes an.

Dieser Algorithmus wird dann bis zu einer vorgegebenen Rekursionstiefe entfaltet: Wird er einmal durchlaufen, entsteht ein Dreieck mit je einem Quadrat über den drei Seiten. Das sieht wie die Illustration zum Satz des Pythagoras aus – daher der Name. Je größer die Rekursionstiefe wird, desto mehr ähnelt das Gebilde einem Baum.

Man kann die beiden ersten Schritte in der obigen Beschreibung überspringen und den rekursiven Prozess mit der Illustration zum Satz des Pythagoras beginnen:

Erzeuge aus dieser Illustration zwei weitere, ihr ähnliche Illustrationen, deren jeweiliges großes Quadrat identisch mit einem der beiden kleinen Quadrate der vorherigen Illustration ist.
Erzeuge nach gleicher Vorschrift aus jeder der im ersten Schritt erzeugten Illustrationen jeweils zwei weitere, ihnen ähnliche Illustrationen usw.

Rekursion in der Grammatik

Die Grammatik natürlicher Sprachen wird in der Linguistik u. a. mit Hilfe von sogenannten Phrasenstrukturregeln beschrieben.[5] Nach Ansicht der meisten Linguisten zeigen dabei alle menschlichen Sprachen[6] die Eigenschaft, rekursiv aufgebaut zu sein (im Gegensatz zu Signalsystemen im Tierreich). Dies ergibt sich, weil in der Zerlegung einer grammatischen Einheit, die mit einer Kategorie etikettiert wird, dieselbe Kategorie erneut auftauchen kann. Ein Beispiel ist das Phänomen der Nebensätze, das hier mit folgender stark vereinfachter Produktionsregel beschrieben ist:

S → NP VP (ein Satz besteht aus einer Nominalphrase (als Subjekt) und einer Verbalphrase)
VP → V NP* (eine Verbalphrase besteht aus einem Verb und null bis vielen Nominalphrasen als Objekten des Verbs)
VP → V S (eine Verbalphrase besteht aus einem Verb und einem Nebensatz als Objekt des Verbs)

Diese Grammatik lässt die Wahl, ob die Ausbuchstabierung von „VP“ mit Regel 2 oder 3 erfolgen soll. Für den Fall, dass die Schritte 1 und dann 3 aufgerufen werden, ergibt sich eine Rekursion: Als Produkt von Regel 3 erscheint das Symbol S, das wiederum den Start für Regel 1 darstellt.[3]

Rekursion in der Mathematik

In der Mathematik spielt Rekursion eine große Rolle, zum Beispiel in der rekursiven Definition von Funktionen. Als Beispiele werden im Folgenden die Berechnung der Fakultät und die Fibonacci-Folge dargestellt. Rekursionsverfahren und rekursive Definition sind in der Mathematik aber nicht auf Funktionen natürlicher Zahlen beschränkt.

Fakultät

Die Funktion Fakultät einer natürlichen Zahl $n\geq 1$ ist definiert als das Produkt der Zahlen 1 bis $n$ :

n!=1\cdot 2\cdot 3\dotsm n=\prod _{k=1}^{n}k

Beispiele

{\begin{array}{rll}1!&=1&=1\\2!&=1\cdot 2&=2\\3!&=1\cdot 2\cdot 3&=6\\4!&=1\cdot 2\cdot 3\cdot 4&=24\\\end{array}}

Soll diese Liste fortgesetzt werden, ergibt sich die Rekursivität nahezu von selbst. Für die Berechnung von 5! wird man nicht von vorn beginnen, sondern kann auf vorherige Ergebnisse zurückgreifen, also

5!=4!\cdot 5=120

Verallgemeinert lässt sich die Funktion somit rekursiv definieren:

n!=\left\{{\begin{matrix}1&&{\text{falls }}n=1&&{\text{(Rekursionsanfang)}}\\(n-1)!\cdot n&&{\text{sonst}}&&{\text{(Rekursionsschritt)}}\end{matrix}}\right.

Die Fibonacci-Folge

Ein klassisches Beispiel für eine rekursive Funktion ist die Fibonacci-Folge, bei der jedes weitere Folgenglied die Summe der beiden vorhergehenden ist:

0,1,1,2,3,5,8,13,21,34,\dotsc

Im Gegensatz zur Fakultätsfunktion gibt es hier keine triviale geschlossene Darstellung. Die einfachste Beschreibung ist die rekursive Definition:

\operatorname {fib} (n)=\left\{{\begin{matrix}0&&{\text{falls }}n=0&&{\text{(Rekursionsanfang)}}\\1&&{\text{falls }}n=1&&{\text{(Rekursionsanfang)}}\\\operatorname {fib} (n-1)+\operatorname {fib} (n-2)&&{\text{sonst}}&&{\text{(Rekursionsschritt)}}\end{matrix}}\right.

Diese rekursive Definition ist kaskadenförmig. Die dritte Fibonacci-Zahl wird anhand dieser Definition folgendermaßen berechnet:

{\begin{matrix}\operatorname {fib} (3)&=&\operatorname {fib} (2)+\operatorname {fib} (1)&{\text{(Rekursionsschritt)}}\\&=&\operatorname {fib} (1)+\operatorname {fib} (0)+\operatorname {fib} (1)&{\text{(Rekursionsschritt)}}\\&=&1+\operatorname {fib} (0)+\operatorname {fib} (1)&{\text{(Rekursionsanfang)}}\\&=&1+0+\operatorname {fib} (1)&{\text{(Rekursionsanfang)}}\\&=&1+0+1&{\text{(Rekursionsanfang)}}\\&=&2\end{matrix}}

Die Berechnung für $\operatorname {fib} (1)$ wird hier mehrfach durchgeführt. Das deutet an, dass es Potential für Optimierungen gibt.

Formale Typen von Rekursion

Die häufigste Rekursionsform ist die lineare Rekursion, bei der in jedem Fall der rekursiven Definition höchstens ein rekursiver Aufruf vorkommen darf. Die Berechnung verläuft dann entlang einer Kette von Aufrufen. Bei einer solchen Rekursion enthält der Aufrufbaum also keine Verzweigungen.

Die primitive Rekursion ist ein Spezialfall der linearen Rekursion, der stets durch eine Iteration ersetzt werden kann (siehe unten #Zum Verhältnis von Rekursion und Iteration). Hier definiert man Funktionen auf den natürlichen Zahlen, wobei in jedem rekursiven Aufruf dessen erster Parameter um Eins ab- oder zunimmt. Jede primitiv-rekursive Definition kann unter Zuhilfenahme eines Stapels durch eine Schleife (z. B. For-Schleife oder While-Schleife) ersetzt werden.

Die endständige oder repetitive Rekursion (Tail Recursion oder Endrekursion) bezeichnet den Spezialfall der linearen Rekursion, bei der jeder rekursive Aufruf die letzte Aktion des rekursiven Aufrufs ist. Endrekursionen lassen sich durch While-Schleifen ersetzen und umgekehrt. (Im Gegensatz zur Endrekursion steht die Head Recursion; siehe unter Infiniter Regress).

Unter verschachtelter Rekursion versteht man eine Rekursion, bei welcher rekursive Aufrufe in Parameterausdrücken rekursiver Aufrufe vorkommen. Diese Rekursionsform gilt als außerordentlich schwer zu durchschauen.

Kaskadenförmige Rekursion bezeichnet den Fall, in dem mehrere rekursive Aufrufe nebeneinander stehen. Die rekursiven Aufrufe bilden dann einen Baum. Kaskadenförmige Rekursion gilt als elegant, kann aber ohne weitere Maßnahmen einen exponentiellen Berechnungsaufwand nach sich ziehen. Sie wird gerne als Ausgangspunkt für die Ableitung einer anderen effizienteren Formulierung gebraucht.

Die wechselseitige Rekursion bezeichnet die Definition mehrerer Funktionen durch wechselseitige Verwendung voneinander. Sie lässt sich auf die gewöhnliche Rekursion einer tupelwertigen Funktion zurückführen.

Rekursion in der Programmierung

Höhere Programmiersprachen, die mit Funktionen arbeiten, erlauben üblicherweise auch die Rekursion. Zumeist lassen sich Lösungen rekursiv oder iterativ angeben.

Zum Verhältnis von Rekursion und Iteration

Rekursion und Iteration sind im Wesentlichen gleich mächtige Vorgehensweisen. Gleiche oder ähnliche Vorgänge werden mehrfach wiederholt, der Unterschied liegt im verwendeten Algorithmus.

Bei einer Iteration lautet der aus mehreren Teilen bestehende Befehl, mehrfach Schleifen (for, while ...) zu durchlaufen, bis eine Abbruchbedingung erfüllt ist. Bei einer Rekursion genügt es, lediglich die Prozeduren oder Funktionen mit der Aufforderung zu ergänzen, dass sie mit einem regelmäßig geänderten Parameter erneut anzuwenden sind, bis eine Abbruchbedingung erfüllt ist.

Eine Rekursion kommt i. d. R. mit weniger Quellcode aus und ist (für erfahrene Anwender) übersichtlicher – es müssen dann keine Hilfsvariablen und Schleifenzähler definiert werden. In der Abarbeitung sind iterative Verfahren meist effizienter und benötigen weniger Speicherplatz. Grund ist das Ablegen der wiederholten Funktionsaufrufe mit allen zwischengespeicherten Werten auf dem Stapelspeicher (Stack). Insbesondere kann die Rekursion auch einen Pufferüberlauf (Stack Overflow) verursachen. Bei der Programmierung von Echtzeitsystemen auf Mikrocontrollern wird daher häufig auf Rekursion verzichtet.

Manche Programmiersprachen (zum Beispiel in der Funktionalen Programmierung) erlauben keine Iteration, sodass immer die rekursive Umsetzung gewählt werden muss. Solche Sprachen setzen zur Optimierung häufig primitive Rekursionen ein, die intern als Iterationen umgesetzt sind (einige Interpreter für LISP und Scheme verfahren so).

Es ist zu beachten, dass eine naive Implementierung bei manchen Funktionen (z. B. den Fibonacci-Zahlen) bedingt, dass Teillösungen mehrfach berechnet werden. Abhilfe schafft in diesem Beispiel die Memoisation, die auf der Wiederverwendung bereits berechneter Zwischenlösungen beruht. Die Rekursion ist ein wesentlicher Bestandteil einiger Entwurfsstrategien für effiziente Algorithmen, insbesondere der Teile-und-herrsche-Strategie (Divide and Conquer). Andere Ansätze (zum Beispiel sogenannte Greedy-Algorithmen) verlangen ein iteratives Vorgehen. Rekursion und primitiv-rekursive Funktionen spielen eine große Rolle in der theoretischen Informatik, insbesondere in der Komplexitätstheorie und Berechenbarkeitstheorie (siehe auch Lambda-Kalkül und Ackermannfunktion).

Im Compilerbau ist der rekursive Abstieg (Recursive Descent) eine Technik, bei der eine Sprache rekursiv geparst wird.

Programmierbeispiele

Das folgende Beispiel zeigt eine einfache und beliebte Implementierung der Fakultätsfunktion in der Programmiersprache Python. Der rekursiven Variante wird hier zur Verdeutlichung eine iterative Variante gegenübergestellt. Die Rekursion kommt dadurch zum Ausdruck, dass die Funktion sich selbst mit einem um 1 verringerten Argument aufruft. Beide Implementierungen führen den Algorithmus mit linearer Laufzeitkomplexität in Abhängigkeit zum Eingabeparameter aus. Während die Platzkomplexität bei der iterativen Variante konstant bleibt, wächst der Speicherbedarf bei der rekursiven Variante linear an, da bei jedem rekursiven Funktionsaufruf ein neuer Speicherbereich für die lokalen Variablen und die Rücksprungadresse reserviert werden muss. Bei der funktionalen Programmierung wird die dynamische Speicherverwaltung durch einen Aufrufstapel realisiert.

Iterative Programmierung	Rekursive Programmierung
def factorial(number): result = 1 while number > 1: result *= number number -= 1 return result	def factorial(number): if number <= 1: return 1 return number * factorial(number - 1)

Das nächste Beispiel implementiert die Fibonacci-Folge in der Programmiersprache C. Bei der rekursiven Variante handelt es sich um eine Mehrfachrekursion, die zu einer exponentiellen Laufzeit- und Platzkomplexität führt. Die rekursiven Funktionsaufrufe verzweigen sich zu einem Binärbaum, bei dem identische Teilergebnisse mehrfach berechnet werden. Am häufigsten werden die Fibonaccizahlen an den ersten beiden Stellen berechnet, welche die Abbruchbedingung in der Rekursion definieren. Bei der iterativen Variante ist die Laufzeitkomplexität linear und die Platzkomplexität konstant.

Iterative Programmierung

Rekursive Programmierung

int fibonacci(int number) {
    int first = 0, second = 1;

    for (int count = 0; count < number; ++count) {
        int summand = first;
        first = second;
        second += summand;
    }

    return first;
}

int fibonacci(int number) {
    if (number <= 0)
        return 0;

    if (number == 1)
        return 1;

    return fibonacci(number - 1) + fibonacci(number - 2);
}

Lösen von Rekursionen

Beim Lösen einer Rekursion sucht man zum einen den Laufzeitaufwand, zum anderen die explizite Form der Rekursion.

Der Aufwand kann als asymptotische Θ- bzw. Ο-Schranke mittels Mastertheorem bzw. Substitutionsmethode bestimmt werden. Auch das geschickte Raten mit anschließender Induktion bietet eine Möglichkeit, eine obere Schranke der Laufzeit zu ermitteln.

Die explizite Form (oder auch geschlossene Form genannt) der Rekursionsgleichung lässt sich beispielsweise durch die Erzeugende Funktion finden. Eine zweite Möglichkeit bietet das Ableiten durch Differenzenbildung aufeinanderfolgender Funktionswerte der Rekurrenz.

Verschiedene Arten des Gebrauchs von Rekursion in verschiedenen und weiteren Wissenschaften

Das Konzept der Rekursion wird in verschiedenen Disziplinen auf unterschiedliche Weise verwendet. Es lassen sich fünf Arten des Gebrauchs unterscheiden: Von der „linear-iterativen“ Rekursion in Mathematik und Informatik und der „generativ-hierarchischen“ Rekursion in Grammatik und Linguistik unterscheiden sich die „organisatorisch-syntaktische“ Rekursion in der Kognitionspsychologie, die „operativ-funktionale“ Rekursion in der Techniktheorie und die „prozessemulative“ Rekursion in der Kulturevolutions- und Zivilisationstheorie.[7]

Kognitionspsychologie

Einen „organisatorisch-syntaktischen“[8] Begriff der Rekursion arbeitete der evolutionäre Kognitionspsychologe Michael Corballis in seinem Buch The Recursive Mind[9] aus. Er zeigt, dass die menschliche Fähigkeit zur prinzipiell beliebig tiefen Verschachtelung von Sinn- und Handlungsebenen und zur offenen syntaktischen Aneinanderreihung von Operationseinheiten, wie sie grundsätzlich im Werkzeugverhalten und der Kooperation auftreten, der Sprachfähigkeit vorausgeht und ein allgemeines Merkmal der menschlichen Kognition und Handlungsorganisation ist. So beruhen die beim Menschen stark ausgeprägten Vermögen zu mentalen Zeitreisen und zur Theory of Mind grundsätzlich auf dem Vermögen zur Rekursion.[10]

Techniktheorie

Einen „operativ-funktionalen“[11] Begriff der Rekursion entwickelte der Systhemtheoretiker W. Brian Arthur in seinem Buch The Nature of Technology[12]. Arthur zeigt, dass alle Technologien eine hierarchische Verschachtelung von Elementen und Funktionsebenen aufweisen, wobei die unteren Elemente ihre operative Funktionalität durch Rekursion zu den oberen Ebenen erhalten, wie er am Beispiel eines Flugzeugträgerverbandes illustriert: Die Turbine eines Kampfjets besteht aus Einzelteilen oder „executables“[13] wie Schrauben und Luftschaufeln, die rekursiv in die Gesamtfunktion der Turbine eingebettet sind, wie zugleich die Turbine ein rekursiv verschachteltes „executable“ des Kampfjets, der Kampfjet ein „executable“ des Flugzeuträgerverbands und dieser ein „executable“ eines Geschwaders ist.[14]

Kulturevolutionforschung und Zivilisationstheorie

Die gesamte technologische und kulturelle Entwicklung in der Kulturevolution und Zivilisationsgeschichte weist das Muster der „prozessemulativen“[15] Rekursion auf, wie der Soziologe Davor Löffler nachgewiesen hat. „Prozessemulative“ Rekursion bezeichnet einen Entwicklungsmechanismus, bei dem ein instrumenteller oder geistiger Vorgang abstrahiert und als materielle oder mediale Emulation wieder eingeführt wird. Dies lässt sich an der frühen Technikevolution nachweisen, in der Entwicklungsstufen jeweils als Grade der Rekursion beschrieben werden können. Dem gegenwärtigen Kenntnisstand nach, zusammengefasst im „Modell der Erweiterung kultureller Kapazitäten“[16], folgen entwicklungsgeschichtlich auf einfache Steinwerkzeuge („Modularkultur“[17], >2,6 Ma) Kompositwerkzeuge wie Hammersteine mit Griff oder Speere mit Knochenspitzen („Kompositkultur“[18], >500 ka), hierauf aus komplementären, voneinander unabhängigen Modulen zusammengesetzte Apparate wie Pfeil-und-Bogen oder Nadel und Faden („Komplementärkultur“[19], >70 ka), hierauf ideelle Werkzeuge wie Höhlenmalereien, Musikinstrumente oder Fallen („ideelle Kultur“[20], >40 ka). Die Technologiestrukturen der kumulativ aufeinander aufbauenden Entwicklungsstufen gründen jeweils auf der „prozessemulativen“ Rekursion der Vorgänge der vorherigen Stufen. Beispielsweise emuliert der Apparat des Pfeil-und-Bogens („Komplementärkultur“) rekursiv den Vorgang des Speerwurfs („Kompositkultur“), und die Falle („ideelle Kultur“) emuliert rekursiv die Anwesenheit einer Jägergruppe bzw. der Fallenmechanismus den Auslösemechanismus des Bogens („Komplementärkultur“). Die „prozessemulative“ Rekursion durchzieht als allgemeines Prinzip die gesamte Technikgeschichte: So beruht beispielsweise der Mikrowellenherd auf der „prozessemulativen“ Rekursion, da darin der Vorgang der Erhitzung von Nahrung etwa durch einen Ofen emuliert wird; die digitale Mustererkennung beruht auf der prozessemulativen Rekursion menschlicher Mustererkennung usw. Es wurde gezeigt, dass das Entwicklungsprinzip der „prozessemulativen“ Rekursion auch den Entwicklungen der gesamten Zivilisationsgeschichte zugrunde liegt und neben der Technologie auch in anderen Bereichen auftritt, etwa der Ökonomie, den Medien, der Politik, der Entwicklung von Kognitionsstrukturen, der Kunst und der Mathematik, wobei wiederum jede Entwicklungsstufe dieser Bereiche auf der rekursiven Emulation der Vorgänge der vorherigen Entwicklungsstufe beruht.[21] So lassen sich kumulativ aufeinander folgende Entwicklungsphasen der Zivilisationsgeschichte (frühe Hochkulturen, Achsenzeit und Neuzeit) als Ausdruck von „prozessemulativen“ Rekursionen erklären.[22]

Siehe auch

Backtracking
Fixpunkt (Mathematik)
Kellerautomat
Logo (Programmiersprache)
Rekursionssatz
Rekursive Sprache
Rekursives Akronym
Selbstähnlichkeit
Türme von Hanoi – typische Anwendung von Rekursion
µ-Rekursion

Weblinks

Wiktionary: Rekursion – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wiktionary: rekursiv – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wikibooks: Rekursive Labyrinthe – Lern- und Lehrmaterialien

Literatur

Niklaus Wirth: Algorithmen und Datenstrukturen. 5. Auflage. B.G. Teubner, Stuttgart 2000. (1. Auflage: 1975). ISBN 978-3-519-22250-7, doi:10.1007/978-3-322-80154-8.

Anmerkungen

Einzelnachweise

Niklaus Wirth, Seite 149: 3. Rekursion, 3.1. Einleitung
Niklaus Wirth: Algorithmen und Datenstrukturen, B. G. Teubner 1983, Seite 150: “Das Wesentliche der Rekursion ist die Möglichkeit, eine unendliche Menge von Objekten durch eine endliche Aussage zu definieren.”
Hadumod Bußmann (Hrsg.): Lexikon der Sprachwissenschaft. Alfred Kröner Verlag, Stuttgart 1990, S. 640: Rekursion ist in der Linguistik ein Begriff, “der die formale Eigenschaft von Grammatiken bezeichnet, mit einem endlichen Inventar von Elementen und einer endlichen Menge von Regeln eine unendliche Menge von Sätzen zu erzeugen.” (zitiert neben Beispielen aus Sprache, Natur, Kunst und Dichtung Mathematik und Programmierung, u. a. z. B. in uni-leipzig: Rekursion in der Sprache).
Douglas R. Hofstadter: Gödel, Escher, Bach, dtv, 2004, Seite 137
Siehe z. B. Andrew Carnie: Constituent Structure. Second edition. Oxford University Press, 2010. Zum Thema Rekursivität v. a. S. 84ff.
Lediglich für die Sprache Pirahã ist die These vorgebracht worden, dass sie keine Rekursion in der Grammatik kennen würde, da es keine Nebensätze gebe. Diese Analyse ist umstritten, für Details siehe den verlinkten Artikel.
Zu diesen fünf Typen siehe Davor Löffler: Generative Realitäten I. Die Technologische Zivilisation als neue Achsenzeit und Zivilisationsstufe. Eine Anthropologie des 21. Jahrhunderts. Weilerswist: Velbrück Wissenschaft, 2019, S. 195–204.
Vgl. Davor Löffler: Generative Realitäten I. Die Technologische Zivilisation als neue Achsenzeit und Zivilisationsstufe. Eine Anthropologie des 21. Jahrhunderts. Weilerswist: Velbrück Wissenschaft, 2019, S. 197 f.
Michael C. Corballis, The Recursive Mind. The Origins of Human Language, Thought, and Civilization. Princeton, NJ/Oxford: Princeton University Press, 2013.
Vgl. Michael C. Corballis: The Recursive Mind. The Origins of Human Language, Thought, and Civilization. Princeton, NJ/Oxford: Princeton University Press, 2013, S. 82–165.
Vgl. Davor Löffler: Generative Realitäten I. Die Technologische Zivilisation als neue Achsenzeit und Zivilisationsstufe. Eine Anthropologie des 21. Jahrhunderts. Weilerswist: Velbrück Wissenschaft, 2019, S. 198 f.
W. Brian Arthur: The Nature of Technology. What It Is and How It Evolves. London: Penguin Books, 2009.
Vgl. W. Brian Arthur: The Nature of Technology. What It Is and How It Evolves. London: Penguin Books, 2009, S. 29
Vgl. W. Brian Arthur: The Nature of Technology. What It Is and How It Evolves. London: Penguin Books, 2009, S. 39–44
Vgl. Davor Löffler: Generative Realitäten I. Die Technologische Zivilisation als neue Achsenzeit und Zivilisationsstufe. Eine Anthropologie des 21. Jahrhunderts. Weilerswist: Velbrück Wissenschaft, 2019, S. 199–204.
Miriam N. Haidle, Michael Bolus, Mark Collard, et al.: The Nature of Culture: An Eight-Grade Model for the Evolution and Expansion of Cultural Capacities in Hominins and other Animals. In: Journal of Anthropological Sciences, Jg. 93, 2015, S. 43–70.
Vgl. Miriam N. Haidle, Michael Bolus, Mark Collard, et al.: The Nature of Culture: An Eight-Grade Model for the Evolution and Expansion of Cultural Capacities in Hominins and other Animals. In: Journal of Anthropological Sciences, Jg. 93, 2015, S. 56 f.
Vgl. Miriam N. Haidle, Michael Bolus, Mark Collard, et al.: The Nature of Culture: An Eight-Grade Model for the Evolution and Expansion of Cultural Capacities in Hominins and other Animals. In: Journal of Anthropological Sciences, Jg. 93, 2015, S. 57 f.
Miriam N. Haidle, Michael Bolus, Mark Collard, et al.: The Nature of Culture: An Eight-Grade Model for the Evolution and Expansion of Cultural Capacities in Hominins and other Animals. In: Journal of Anthropological Sciences, Jg. 93, 2015, S. 58.
Miriam N. Haidle, Michael Bolus, Mark Collard, et al.: The Nature of Culture: An Eight-Grade Model for the Evolution and Expansion of Cultural Capacities in Hominins and other Animals. In: Journal of Anthropological Sciences, Jg. 93, 2015, S. 58–60.
Eine zusammenfassende Tabelle findet sich in Davor Löffler: Generative Realitäten I. Die Technologische Zivilisation als neue Achsenzeit und Zivilisationsstufe. Eine Anthropologie des 21. Jahrhunderts. Weilerswist: Velbrück Wissenschaft, 2019, S. 600 f.
Vgl. Davor Löffler: Generative Realitäten I. Die Technologische Zivilisation als neue Achsenzeit und Zivilisationsstufe. Eine Anthropologie des 21. Jahrhunderts. Weilerswist: Velbrück Wissenschaft, 2019, S. 621–640.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Niklaus Wirth, Seite 149: 3. Rekursion, 3.1. Einleitung

[2] Niklaus Wirth: Algorithmen und Datenstrukturen, B. G. Teubner 1983, Seite 150: “Das Wesentliche der Rekursion ist die Möglichkeit, eine unendliche Menge von Objekten durch eine endliche Aussage zu definieren.”

[Buss-3] Hadumod Bußmann (Hrsg.): Lexikon der Sprachwissenschaft. Alfred Kröner Verlag, Stuttgart 1990, S. 640: Rekursion ist in der Linguistik ein Begriff, “der die formale Eigenschaft von Grammatiken bezeichnet, mit einem endlichen Inventar von Elementen und einer endlichen Menge von Regeln eine unendliche Menge von Sätzen zu erzeugen.” (zitiert neben Beispielen aus Sprache, Natur, Kunst und Dichtung Mathematik und Programmierung, u. a. z. B. in uni-leipzig: Rekursion in der Sprache).

[4] Douglas R. Hofstadter: Gödel, Escher, Bach, dtv, 2004, Seite 137

[5] Siehe z. B. Andrew Carnie: Constituent Structure. Second edition. Oxford University Press, 2010. Zum Thema Rekursivität v. a. S. 84ff.

[6] Lediglich für die Sprache Pirahã ist die These vorgebracht worden, dass sie keine Rekursion in der Grammatik kennen würde, da es keine Nebensätze gebe. Diese Analyse ist umstritten, für Details siehe den verlinkten Artikel.

[7] Zu diesen fünf Typen siehe Davor Löffler: Generative Realitäten I. Die Technologische Zivilisation als neue Achsenzeit und Zivilisationsstufe. Eine Anthropologie des 21. Jahrhunderts. Weilerswist: Velbrück Wissenschaft, 2019, S. 195–204.

[8] Vgl. Davor Löffler: Generative Realitäten I. Die Technologische Zivilisation als neue Achsenzeit und Zivilisationsstufe. Eine Anthropologie des 21. Jahrhunderts. Weilerswist: Velbrück Wissenschaft, 2019, S. 197 f.

[9] Michael C. Corballis, The Recursive Mind. The Origins of Human Language, Thought, and Civilization. Princeton, NJ/Oxford: Princeton University Press, 2013.

[10] Vgl. Michael C. Corballis: The Recursive Mind. The Origins of Human Language, Thought, and Civilization. Princeton, NJ/Oxford: Princeton University Press, 2013, S. 82–165.

[11] Vgl. Davor Löffler: Generative Realitäten I. Die Technologische Zivilisation als neue Achsenzeit und Zivilisationsstufe. Eine Anthropologie des 21. Jahrhunderts. Weilerswist: Velbrück Wissenschaft, 2019, S. 198 f.

[12] W. Brian Arthur: The Nature of Technology. What It Is and How It Evolves. London: Penguin Books, 2009.

[13] Vgl. W. Brian Arthur: The Nature of Technology. What It Is and How It Evolves. London: Penguin Books, 2009, S. 29

[14] Vgl. W. Brian Arthur: The Nature of Technology. What It Is and How It Evolves. London: Penguin Books, 2009, S. 39–44

[15] Vgl. Davor Löffler: Generative Realitäten I. Die Technologische Zivilisation als neue Achsenzeit und Zivilisationsstufe. Eine Anthropologie des 21. Jahrhunderts. Weilerswist: Velbrück Wissenschaft, 2019, S. 199–204.

[16] Miriam N. Haidle, Michael Bolus, Mark Collard, et al.: The Nature of Culture: An Eight-Grade Model for the Evolution and Expansion of Cultural Capacities in Hominins and other Animals. In: Journal of Anthropological Sciences, Jg. 93, 2015, S. 43–70.

[17] Vgl. Miriam N. Haidle, Michael Bolus, Mark Collard, et al.: The Nature of Culture: An Eight-Grade Model for the Evolution and Expansion of Cultural Capacities in Hominins and other Animals. In: Journal of Anthropological Sciences, Jg. 93, 2015, S. 56 f.

[18] Vgl. Miriam N. Haidle, Michael Bolus, Mark Collard, et al.: The Nature of Culture: An Eight-Grade Model for the Evolution and Expansion of Cultural Capacities in Hominins and other Animals. In: Journal of Anthropological Sciences, Jg. 93, 2015, S. 57 f.

[19] Miriam N. Haidle, Michael Bolus, Mark Collard, et al.: The Nature of Culture: An Eight-Grade Model for the Evolution and Expansion of Cultural Capacities in Hominins and other Animals. In: Journal of Anthropological Sciences, Jg. 93, 2015, S. 58.

[20] Miriam N. Haidle, Michael Bolus, Mark Collard, et al.: The Nature of Culture: An Eight-Grade Model for the Evolution and Expansion of Cultural Capacities in Hominins and other Animals. In: Journal of Anthropological Sciences, Jg. 93, 2015, S. 58–60.

[21] Eine zusammenfassende Tabelle findet sich in Davor Löffler: Generative Realitäten I. Die Technologische Zivilisation als neue Achsenzeit und Zivilisationsstufe. Eine Anthropologie des 21. Jahrhunderts. Weilerswist: Velbrück Wissenschaft, 2019, S. 600 f.

[22] Vgl. Davor Löffler: Generative Realitäten I. Die Technologische Zivilisation als neue Achsenzeit und Zivilisationsstufe. Eine Anthropologie des 21. Jahrhunderts. Weilerswist: Velbrück Wissenschaft, 2019, S. 621–640.