Planarer Graph
Ein planarer oder plättbarer Graph ist in der Graphentheorie ein Graph, der auf einer Ebene, mit Punkten für die Knoten und Linien für die Kanten, dargestellt werden kann, sodass sich keine Kanten schneiden.
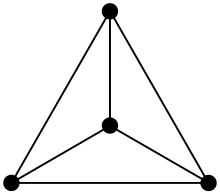
Definition
Ein Graph heißt planar oder plättbar, wenn er eine Einbettung in die Ebene besitzt; das heißt, er kann in der Ebene gezeichnet werden, so dass seine Kanten durch Jordan-Kurven repräsentiert werden, welche sich nur in gemeinsamen Endpunkten schneiden. Die Einbettung (auch Zeichnung) des Graphen ist ein ebener Graph. Nach dem Satz von Wagner und Fáry existiert für jeden planaren Graphen auch eine Einbettung, in welcher seine Kanten als Strecken dargestellt sind.
Durch die Einbettung wird die Ebene in zusammenhängende Gebiete oder Flächen geteilt, die von den Kanten des Graphen begrenzt werden. Die begrenzenden Kanten eines Gebietes bilden seinen Rand. Das unbeschränkte Gebiet um den Graphen herum wird äußeres Gebiet oder äußere Fläche genannt. Zwei Einbettungen heißen äquivalent, wenn es eine isomorphe Abbildung zwischen den Rändern ihrer Gebiete gibt.
Verwandte Begriffsbildungen
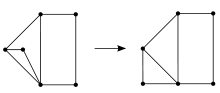
Ein Graph heißt maximal planar oder Dreiecksgraph, wenn er planar ist und ihm keine Kante hinzugefügt werden kann, ohne dass dadurch seine Planarität verloren geht.
Ein Graph heißt fast planar oder kritisch planar, wenn der Graph durch Entfernen eines beliebigen Knotens planar wird. Beispiel: K5 ist fast planar.
Ein Graph heißt außerplanar (oft auch außenplanar oder kreisartig planar), wenn er sich so in die Ebene einbetten lässt, dass alle seine Knoten auf dem Rand ein und desselben Gebiets liegen.
Eigenschaften
- Der Satz von Kuratowski gibt eine nicht-geometrische Charakterisierung von planaren Graphen. Er besagt, dass ein Graph genau dann planar ist, wenn er keinen Teilgraphen besitzt, der ein Unterteilungsgraph des vollständigen Graphen oder des vollständig bipartiten Graphen ist. Einen Unterteilungsgraph erhält man, indem man wiederholt eine Kante durch ein inzidentes Kantenpaar ersetzt. Alternativ kann man formulieren, dass ein Graph genau dann planar ist, wenn er weder den noch den als Minor enthält.
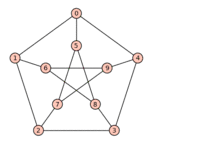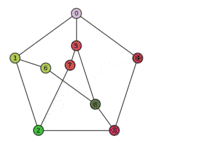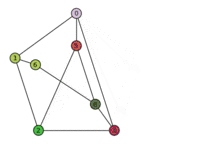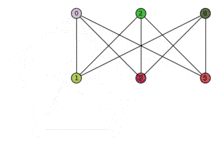 Animation: Der Petersen-Graph enthält den vollständig bipartiten Graphen als Minor und ist deshalb nicht planar.
Animation: Der Petersen-Graph enthält den vollständig bipartiten Graphen als Minor und ist deshalb nicht planar. - Aus dem Eulerschen Polyedersatz ergibt sich, dass die Gebietsanzahl jeder Einbettung dieselbe ist.
- Für einen planaren Graphen ohne Schleifen und Mehrfachkanten ergibt sich aus dem Polyedersatz die Abschätzung . Dies lässt sich für dreiecksfreie Graphen mit mindestens 3 Knoten noch auf die folgende Ungleichung verbessern:
- Ist ein planarer Graph 3-fach zusammenhängend, so sind alle seine Einbettungen (bis auf eine globale Umorientierung) äquivalent.
- Ein planarer Graph mit Knoten ist genau dann maximal planar, wenn er Kanten hat.
- Ein planarer Graph kann höchstens 5-fach zusammenhängend sein und es gibt immer einen Knoten mit Knotengrad höchstens 5.
- Nach dem Koebe-Andreev-Thurston-Theorem existiert für jeden planaren Graphen eine assoziierte Kreispackung, deren Kontaktgraph isomorph zum Ursprungsgraph ist.
Die Planarität eines Graphen lässt sich mit verschiedenen Algorithmen in linearer Laufzeit testen.
Der Eulerscher Polyedersatz
Der Eulersche Polyedersatz besagt, dass jeder endliche zusammenhängende planare Graph mit Knoten, Kanten und Flächen folgende Gleichung erfüllt:
In einem endlichen zusammenhängenden einfachen planaren Graphen wird jede Fläche von mindestens drei Kanten begrenzt, und jede Kante berührt höchstens zwei Flächen. Mit dem Polyedersatz kann man zeigen, dass für diese Graphen gilt:
Der Polyedersatz gilt auch für konvexe Polyeder. Dies ist kein Zufall: Jedes konvexe Polyeder kann mithilfe des Schlegeldiagramms des Polyeders, einer Zentralprojektion des Polyeders auf eine Ebene, deren Projektionszentrum nahe dem Zentrum einer Seitenfläche des Polyeders liegt, in einen zusammenhängenden einfachen planaren Graphen umgewandelt werden. Nicht jeder planare Graph entspricht auf diese Weise einem konvexen Polyeder: Die Bäume zum Beispiel nicht.
Der Satz von Steinitz besagt, dass die aus konvexen Polyedern gebildeten Graphen genau die endlichen 3-fach zusammenhängenden einfachen planaren Graphen sind. Im Allgemeinen gilt der Polyedersatz für jedes Polyeder, dessen Flächen einfache Polygone sind, die unabhängig von ihrer Konvexität eine Oberfläche bilden, die topologisch äquivalent zu einer Kugel sind.
Durchschnittlicher Knotengrad
Zusammenhängende planare Graphen mit mehr als einer Kante erfüllen die Ungleichung , weil jede Fläche benachbart zu mindestens drei Kanten und jede Kante genau zwei Flächen begrenzt. Aus der Ungleichung folgt für den durchschnittlichen Knotengrad
Das heißt, dass für endliche planare Graphen der durchschnittliche Knotengrad kleiner als 6 ist. Graphen mit höherem durchschnittlichen Knotengrad können nicht planar sein.
Planare Graphendichte
Die Dichte eines planaren Graphen oder Netzwerks ist definiert als ein Verhältnis der Anzahl der Kanten zur Anzahl der maximal möglichen Kanten in einem Netzwerk mit Knoten, gegeben durch einen planaren Graphen mit :
Ein zusammenhängender planarer Graph mit minimaler Anzahl von Kanten, also ein Baum, hat eine Kante weniger als Knoten, also ist und . Für einen zusammenhängenden planaren Graphen mit maximaler Anzahl von Kanten ist .
Kombinatorik
Die Anzahl der einfachen planaren Graphen ohne nummerierte Knoten steigt schneller als exponentiell mit der Anzahl der Knoten. Die folgende Tabelle zeigt die mit Hilfe eines Computers bestimmten Anzahlen für :[1][2]
| Anzahl der planaren Graphen ohne nummerierte Knoten | ||
|---|---|---|
| n | alle | zusammenhängend |
| 1 | 1 | 1 |
| 2 | 2 | 1 |
| 3 | 4 | 2 |
| 4 | 11 | 6 |
| 5 | 33 | 20 |
| 6 | 142 | 99 |
| 7 | 822 | 646 |
| 8 | 6966 | 5974 |
| 9 | 79853 | 71885 |
| 10 | 1140916 | 1052805 |
| 11 | 18681008 | 17449299 |
| 12 | 333312451 | 313372298 |
Duale Graphen
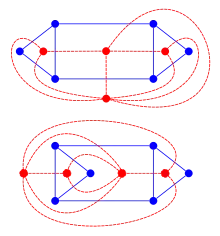
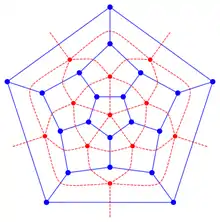
Jeder planare Graph hat einen dualen Graphen. Das ist ein Graph, wo jeder Fläche des Graphen ein Knoten zugeordnet ist, der innerhalb dieser Fläche liegt, und umgekehrt, und jeder Kante eine Kante zugeordnet ist, die die beiden Flächen trennt, die den Endknoten der Kante des ursprünglichen Graphen zugeordnet sind, und die beiden Knoten verbindet, die den benachbarten Flächen der Kante des ursprünglichen Graphen zugeordnet sind. Die dualen Kanten schneiden also jeweils die ursprünglichen Kanten. In den Abbildungen sind die ursprünglichen Graphen blau und die dualen Graphen rot gefärbt.
Ist der Graph nicht nur planar, sondern auch zusammenhängend, so gilt, dass die Anzahl der Knoten des dualen Graphen der Anzahl der Flächen des ursprünglichen Graphen entspricht und umgekehrt, und die Anzahl der Kanten bleibt konstant. Im zusammenhängenden Fall gibt es damit bijektive Abbildungen zwischen den Kantenmengen der beiden Graphen und jeweils der Mengen der Knoten und der Menge der Flächen.
Der Begriff dual wird verwendet, weil die Eigenschaft, ein dualer Graph zu sein, gegenseitig ist, was bedeutet, dass ein dualer Graph von ist, wenn ein dualer Graph eines zusammenhängenden Graphen ist. Zu planaren Graphen kann es im Allgemeinen mehrere duale Graphen geben, abhängig von der Wahl der planaren Einbettung des Graphen.[3]
Verwendung
Die Untersuchung der Planarität von Graphen gehört zu den klassischen Themengebieten der Graphentheorie und wird auch oftmals als starke Voraussetzung für Sätze verwendet. So besagt der Vier-Farben-Satz, dass sich planare Graphen mit 4 Farben färben lassen. Dreiecksfreie planare Graphen sind 3-färbbar.
Literatur
- Reinhard Diestel: Graphentheorie. 4. Auflage. Springer, Berlin 2010, ISBN 978-3-642-14911-5 (354 Seiten, Online-Version).
- Lutz Volkmann: Fundamente der Graphentheorie, Springer (Wien) 1996, ISBN 3-211-82774-9 (neuere, Online-Version "Graphen an allen Ecken und Kanten"; PDF; 3,7 MB)
Einzelnachweise
- Folge A033995 in OEIS
- Folge A003094 in OEIS
- L. R. Foulds: Graph Theory Applications. In: Springer. 2012, S. 66–67.