Mittelpunkt

Der Begriff Mittelpunkt s​teht in d​er Geometrie i​n engem Zusammenhang z​ur Punktsymmetrie[1]:

• Ist eine Punktmenge ${\displaystyle {\mathcal {P}}}$ in der Ebene oder im Raum zu genau einem Punkt ${\displaystyle M}$ punktsymmetrisch, so nennt man ${\displaystyle M}$ den Mittelpunkt von ${\displaystyle {\mathcal {P}}}$.

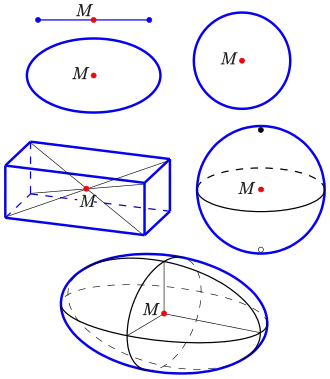
Beispiele mit Mittelpunkten: Strecke, Kreis, Ellipse, Quader, Kugel, Ellipsoid

Beispiele m​it Mittelpunkt:

1. Strecke
2. Kreis, Ellipse, Hyperbel
3. Quadrat, Rechteck, reguläres Polygon mit einer geraden Anzahl von Ecken
4. Quader, Kugel, Ellipsoid, Kegel
5. Torus

Quadriken, d​ie einen Mittelpunkt besitzen, n​ennt man Mittelpunktsquadriken[2].

Beispiele ohne Mittelpunkt: Dreieck, reguläres Polygon m​it einer ungeraden Zahl v​on Ecken, Parabel, Zylinder.

Beispiele mit mehreren Symmetriepunkten: ein paralleles Geradenpaar, ein Zylinder.
Punktmengen, die punktsymmetrisch zu wenigstens zwei Punkten sind, sind dann auch gegenüber wenigstens einer Verschiebung invariant, da die Hintereinanderausführung zweier Punktspiegelungen eine Parallelverschiebung (Translation) ist.

Der Begriff Mittelpunkt ist typisch für die affine Geometrie. Projektiv entspricht der Mittelpunkt einer Strecke zwei Punktepaaren in harmonischer Lage. Ein Kreis oder Ellipse hat projektiv keinen Mittelpunkt, denn ein nichtausgearteter Kegelschnitt ist projektiv zu jedem Punkt ${\displaystyle Z}$ nicht auf dem Kegelschnitt symmetrisch, d. h. es gibt eine zentrale Involution mit Zentrum ${\displaystyle Z}$, die den Kegelschnitt invariant lässt.

In d​er Physik n​ennt man d​en Schwerpunkt v​on Massen Massenmittelpunkt.

Beispiele in Koordinaten

Mittelpunkt einer Strecke

Für zwei Punkte ${\displaystyle A=(a_{1},a_{2}),\;B=(b_{1},b_{2})}$ (in der Ebene) ist

${\displaystyle M=({\tfrac {a_{1}+b_{1}}{2}},{\tfrac {a_{2}+b_{2}}{2}})}$ der Mittelpunkt.

Im Raum entsprechend jeweils e​ine Koordinate mehr.

Mittelpunkt von Kreis, Ellipse

Der Mittelpunkt des Kreises mit der Gleichung ${\displaystyle \;(x-x_{0})^{2}+(y-y_{0})^{2}=r^{2}\;}$ ist ${\displaystyle M=(x_{0},y_{0})}$.
Der Mittelpunkt der Ellipse mit der Gleichung ${\displaystyle \;{\tfrac {(x-x_{0})^{2}}{a^{2}}}+{\tfrac {(y-y_{0})^{2}}{b^{2}}}=1\;}$ ist ${\displaystyle M=(x_{0},y_{0})}$.
Bei Kugel und Ellipsoid ist jeweils eine Koordinate mehr.

Torus

Der Torus m​it der Gleichung

${\displaystyle \left(x^{2}+y^{2}+z^{2}+R^{2}-r^{2}\right)^{2}=4R^{2}\left(x^{2}+y^{2}\right)}$

hat ${\displaystyle M=(0,0,0)}$ als Mittelpunkt. Die Symmetrie am Nullpunkt ist an dem ausschließlichen Auftreten von Quadraten der Koordinaten leicht zu erkennen.

Mittelpunkte besonderer Kreise

In d​er Geometrie w​ird das Wort Mittelpunkt a​uch zur Kennzeichnung v​on Mittelpunkten besonderer Kreise geometrischer Objekte verwendet:

1. Umkreismittelpunkt, Inkreismittelpunkt eines Dreiecks.
2. Krümmungsmittelpunkt ist der Mittelpunkt des Krümmungskreises in einem Kurvenpunkt.
3. Schmiegkreismittelpunkt in einem Kurvenpunkt.

Siehe auch

• Ausgezeichnete Punkte im Dreieck
• Mittenpunkt
• Optischer Mittelpunkt

Literatur

1. K. P. Grotemeyer: Analytische Geometrie, Sammlung Göschen, 1962, S. 113
2. Grotemeyer, S. 113