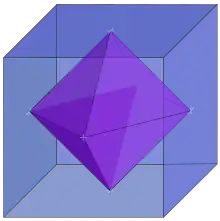
Polyeder
Ein Polyeder [poliˈ(ʔ)eːdɐ] (auch Vielflächner; von altgriechisch πολύεδρος polýedros, deutsch ‚vielsitzig, vieleckig‘)[1] ist ein dreidimensionaler Körper, der ausschließlich von ebenen Flächen begrenzt wird.
Das Analogon im Zweidimensionalen ist das Polygon, im Vierdimensionalen das Polychor, allgemein das -dimensionale Polytop.
Beispiele sind der Würfel als beschränktes Polyeder und ein Oktant eines dreidimensionalen Koordinatensystems als unbeschränktes Polyeder.
Eigenschaften
Polyeder weisen neben planaren Flächen auch ausschließlich geradlinige Kanten auf, da sich planare Flächen als Teilmenge von Ebenen nur in Geraden schneiden.
Polyeder weisen folgende Eigenschaften auf:
Topologie
- Anzahl und Art der Seitenflächen
- Anzahl und Länge der Kanten
- Anzahl der Ecken
- Anzahl der Flächen/Kanten in jeder Ecke
Größen
- Volumen (wenn jede Fläche eine eindeutige Orientierung hat)
- Oberflächeninhalt
- Gesamtlänge der Kanten
Einige Polyeder haben außerdem Symmetrieeigenschaften, zum Beispiel
Die platonischen Körper definieren außerdem Symmetriegruppen, nämlich die Tetraedergruppe, die Oktaedergruppe und die Ikosaedergruppe.
Konstruktion
Konstruiert werden können Polyeder sowohl auf Basis ihrer Eckpunkte als auch ihrer planaren Flächen.
Konstruktion aus ihren Eckpunkten
Konstruieren lassen sich Polyeder, indem mindestens vier Punkte (die nicht in einer Ebene liegen) durch Kanten miteinander verbunden werden. Die Eckenanzahl der entstehenden Begrenzungsflächen ist davon abhängig, wie viele Punkte jeweils in dieser Ebene liegen. Da drei Punkte je eine Ebene aufspannen, entstehen mindestens Dreiecke. Liegen vier oder mehr Punkte „geschickt“ in einer Ebene, entstehen als Begrenzungsflächen Vier- oder Mehrecke.
Konstruktion aus ihren Flächen
Konstruieren lassen sich Polyeder, indem der Raum durch mindestens vier Ebenen geteilt wird. Die Anzahl der notwendigen Ebenen ist die Anzahl der Flächen des Polyeders. Schnittpunkte zweier Ebenen bilden die Kanten des Polyeders (Anzahl ), die Schnittpunkte dreier oder mehrerer Ebenen die Eckpunkte (Anzahl ). Damit sich in einer Ecke mehr als drei Ebenen bzw. Flächen treffen, müssen sich „geschickt“ mehr als drei Ebenen in einem Punkt treffen.
Besondere Polyeder
Polyeder, wie sie uns im Alltag begegnen bzw. wie man sie von der Schulmathematik her kennt (vgl. vorhergehender Abschnitt), sind dreidimensional und beschränkt, also – im Sinne der Topologie – kompakte Teilmengen des dreidimensionalen euklidischen Raums. Sie zählen damit zu den geometrischen Körpern. Ein Polyeder heißt dabei dreidimensional, wenn es in keiner Ebene vollständig enthalten ist. Ein Polyeder heißt beschränkt, wenn es eine Kugel gibt, in der es vollständig enthalten ist. Unbeschränkte Polyeder mit nur einer Ecke werden Polyederkegel genannt. Dazu zählen etwa die Trieder (englisch trihedron).
Konvexe Polyeder
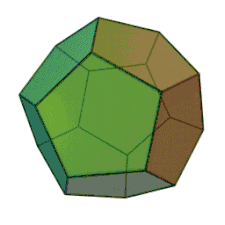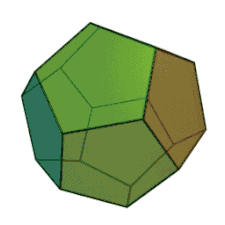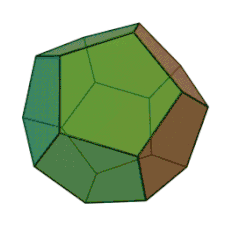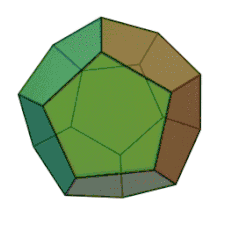
Häufig sind dreidimensionale Polyeder zudem konvex. Ein Polyeder heißt konvex, wenn für je zwei Punkte des Polyeders die Verbindungsstrecke zwischen diesen Punkten vollständig im Polyeder liegt. Zum Beispiel ist das nebenstehende Dodekaeder konvex. Ein Beispiel eines nicht-konvexen Polyeders ist das unten gezeigte toroidale Polyeder.
Reguläre Polyeder, platonische, archimedische, catalanische und Johnson-Körper
Polyeder können nach verschiedenen Arten von Regelmäßigkeiten klassifiziert werden. Die wichtigsten sind:
- Alle Seitenflächen sind regelmäßige Vielecke.
- Alle Seitenflächen sind kongruent (deckungsgleich).
- Alle Ecken sind gleichartig, das heißt, für je zwei Ecken kann man das Polyeder so drehen oder spiegeln, dass in überführt wird und das neue Polyeder mit dem ursprünglichen zur Deckung kommt.
- Alle Winkel zwischen benachbarten Flächen (Diederwinkel) sind gleich.
Klassifizierung Anzahl 1. 2. 3. 4. konvex Bemerkungen platonische Körper 5 




jeweils dual zu einem platonischen Körper Kepler-Poinsot-Körper 4 




jeweils dual zu einem Kepler-Poinsot-Körper reguläre Polyeder 9 



– gemeinsame Definition für platonische Körper und Kepler-Poinsot-Körper archimedische Körper 13 




jeweils dual zu einem catalanischen Körper catalanische Körper 13 




jeweils dual zu einem archimedischen Körper reguläre Prismen geeigneter Höhe 




die Seitenflächen sind 2 reguläre n-Ecke und n Quadrate, Ausschlusskriterium für archimedische Körper reguläre Antiprismen geeigneter Höhe 




die Seitenflächen sind 2 reguläre n-Ecke und 2·n gleichseitige Dreiecke, Ausschlusskriterium für archimedische Körper reguläre Doppelpyramiden geeigneter Höhe 




die Seitenflächen sind 2·n gleichseitige Dreiecke, Ausschlusskriterium für catalanische Körper reguläre Trapezoeder geeigneter Höhe 




die Seitenflächen sind 2·n Drachenvierecke, Ausschlusskriterium für catalanische Körper Johnson-Körper 92 




alle Seitenflächen sind reguläre Polygone
Orthogonale Polyeder
Die Flächen eines orthogonalen Polyeders treffen sich im rechten Winkel. Seine Kanten verlaufen parallel zu den Achsen eines kartesischen Koordinatensystems. Mit Ausnahme des Quaders sind orthogonale Polyeder nicht konvex. Sie erweitern die zweidimensionalen orthogonalen Polygone in die dritte Dimension. Orthogonale Polyeder kommen in der algorithmischen Geometrie zum Einsatz. Dort bietet ihre eingeschränkte Struktur Vorteile beim Bewältigen ansonsten ungelöster Probleme (beliebiger Polyeder). Ein Beispiel ist das Entfalten der Polyederflächen in ein polygonales Netz.
Chirale Polyeder
Chirale Polyeder sind Vielflächner, die topologisch nicht mit ihrem Spiegelbild übereinstimmen. Beispiele in drei Dimensionen sind der abgeschrägte Würfel und das schiefe Dekaeder. Sie weisen Händigkeit auf, das heißt, sie besitzen eine rechtshändige und eine linkshändige Variante, die durch Spiegelung aufeinander abgebildet werden können.[2]
Apeiroeder

Apeiroeder sind unbeschränkte Polyeder mit sich wiederholenden Strukturen.
Polyeder im Alltag
Beispiele für Polyeder aus dem Alltag – verstanden als geometrische Körper – sind in ihrer üblichen Bauweise – Schränke, Pyramiden, Häuser, Kristalle, Spielwürfel und Geodätische Kuppeln. Keine Polyeder sind hingegen Kugeln, Kegel, Flaschen, Tortenstücke, da sie gekrümmte Randflächen besitzen.
Eulerscher Polyedersatz und Euler-Charakteristik
Für konvexe und beschränkte Polyeder gilt der eulersche Polyedersatz:
Dabei ist die Anzahl der Ecken, die Anzahl der Kanten und die Anzahl der Flächen.
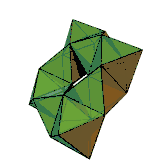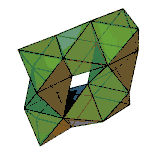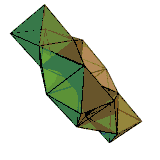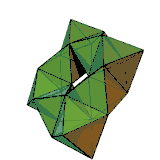
Für zusammenhängende Polyeder gilt allgemein
mit der Euler-Charakteristik . Für einen Torus zum Beispiel ist . Das rechts abgebildete Polyeder ist ein Beispiel dafür. Es hat 24 Ecken, 72 Kanten und 48 Flächen: .
Für alle Polyeder ist die Anzahl der Flächen mit ungerader Eckenanzahl (die jeweils gleich der Anzahl der Kanten ist) gerade. Das folgt daraus, dass die Summe der Anzahl der Kanten aller Seitenflächen gerade ist, weil diese Summe die doppelte Anzahl der Kanten des Polyeders ist.
Außerdem ist für alle Polyeder die Anzahl der Ecken, wo eine ungerade Anzahl von Flächen (die jeweils gleich der Anzahl der Kanten ist) zusammentrifft, gerade. Das folgt daraus, dass die Summe der Anzahl der Kanten, die an den Ecken zusammentreffen, gerade ist, weil diese Summe die doppelte Anzahl der Kanten des Polyeders ist.
Für jedes konvexe Polyeder gilt die Ungleichung , weil jede Fläche benachbart zu mindestens 3 Kanten ist und jede Kante genau 2 Flächen begrenzt. Daraus und aus der Gleichung (Eulerscher Polyedersatz) folgt . Außerdem gilt , weil in jeder Ecke mindestens 3 Kanten zusammentreffen und zu jeder Kante genau 2 Ecken gehören. Daraus und aus dem eulerschen Polyedersatz folgt .
Ein konvexes Polyeder mit Flächen hat also mindestens und höchstens Ecken. Daraus folgt außerdem, dass ein Polyeder mit Ecken mindestens und maximal Flächen hat.

Bei gegebener Anzahl von Flächen wird die minimale Anzahl von Ecken erreicht, wenn das Polyeder nur von Dreiecksflächen begrenzt wird, d. h. von Polygonen mit 3 Kanten und 3 Ecken. Das ist unter anderem beim Tetraeder, beim Oktaeder, beim Ikosaeder, bei den Deltaedern, bei einigen catalanischen Körpern und bei allen Doppelpyramiden der Fall. Weitere Beispiele sind die geodätischen Polyeder (siehe auch: en:Geodesic polyhedron).

Bei gegebener Anzahl von Flächen wird stattdessen die maximale Anzahl von Ecken erreicht, wenn sich in jeder Ecken immer nur 3 Flächen und 3 Kanten treffen. Das ist unter anderem beim Tetraeder, beim Würfel, beim Dodekaeder, bei einigen archimedischen Körpern und bei allen Prismen der Fall. Weitere Beispiele sind die Goldberg-Polyeder (siehe auch: en:Goldberg polyhedron).
Diese Polyeder weisen für eine gegebene Anzahl von Flächen (oder Ecken) auch jeweils das Minimum oder das Maximum an Kanten auf.
Beispiele für Polyeder mit einer bestimmten Flächenzahl
Polyeder werden nur in Ausnahmefällen (im Allgemeinen der Körper mit maximaler Symmetrie, die platonischen Körper) nach der Anzahl der begrenzenden Flächen klassifiziert.
So versteht man unter Oktaeder (3,3,3,3,3,3,3,3) eher einen platonischen Körper als einen Zylinder mit sechsseitiger Grundfläche (6,6,4,4,4,4,4,4).
Die Anzahl von Polyedern mit verschiedenen Topologien bei gegebener Seitenanzahl wächst überexponential mit der Seitenanzahl.
- Ein Tetraeder ist eindeutig.
- Ein Pentaeder ist eine fünfseitige Pyramide oder ein dreiseitiges Prisma.
- Bei Hexaedern gibt es schon 7 konvexe und 4 konkave Polyeder.
- Bei Oktaedern gibt es schon 257 konvexe Polyeder, hinzu kommt noch eine größere Zahl an konkaven Polyedern.
- Bei Dodekaedern gibt es schon mehr als 6 Millionen konvexe Polyeder, bei Tetradekaeder wird schon die Milliarde erreicht.
Der Name eines Polyeders weist im Allgemeinen auf dessen Verwandtschaft und dessen Konstruktionsprinzip hin, manchmal auch auf Gegenstände des alltäglichen Lebens. Polyeder, deren Name „-dekaeder“ enden, brauchen nicht einmal 12 Flächen zu haben (Ausgehöhltes Dodekaeder mit 20 Flächen), teilweise gibt es nur in der Konstruktionskette Zwölfflächner oder Polyeder, die von einer bestimmten Polygonart 12 Flächen haben (Rhombenikosidodekaeder mit 62 Flächen).
| F | allgemein | Beispiel | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Name | K | E | Name | Bild | K | E | |||
| 4 | Tetraeder | 6 | 4 | Dreieckpyramide | 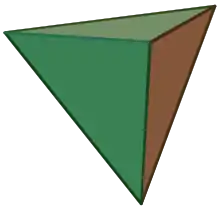 |
6 | 4 | ||
| 5 | Pentaeder | 8...9 | 5...6 | Quadratpyramide | 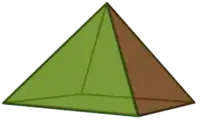 |
8 | 5 | ||
| 6 | Hexaeder | 9...12 | 5...8 | Würfel | 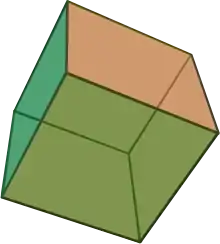 |
12 | 8 | ||
| 7 | Heptaeder | 11...15 | 6...10 | verlängerte Dreieckpyramide |  |
12 | 7 | ||
| 8 | Oktaeder | 12...18 | 6...12 | Rhomboederstumpf | 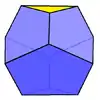 |
18 | 12 | ||
| 9 | Enneaeder | 14...21 | 7...14 | verlängerte Quadratpyramide | 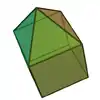 |
16 | 9 | ||
| 10 | Dekaeder | 15...24 | 7...16 | Fünfeck-Bipyramide | .svg.png.webp) |
15 | 7 | ||
| 11 | Hendekaeder | 17...27 | 8...18 | ? |  |
20 | 11 | ||
| 12 | Dodekaeder | 18...30 | 8...20 | regelmäßiges Dodekaeder |  |
30 | 20 | ||
| 13 | Tridekaeder | 9...22 | verdreht verlängerte Quadratpyramide | 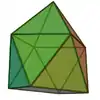 |
20 | 9 | |||
| 14 | Tetradekaeder | 9...24 | Disheptaeder | 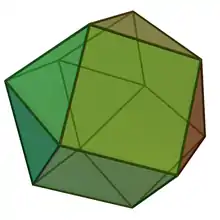 |
24 | 12 | |||
| 15 | Pentadekaeder | 10...26 | verlängerte Fünfecks- Bipyramide |  |
25 | 12 | |||
| 16 | Hexadekaeder | 10...28 | zweifach erweitertes Antiprisma | 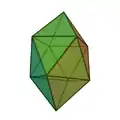 |
24 | 10 | |||
| 17 | Heptadekaeder | 11...30 | erweiterte Sphenocorona |  |
26 | 11 | |||
| 18 | Oktadekaeder | 11...32 | Quadratdoppelkuppel | 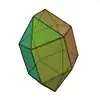 |
32 | 16 | |||
| 20 | Ikosaeder | 12...36 | regelmäßiges Ikosaeder |  |
30 | 12 | |||
| 22 | Ikosidiplo- eder | 13...40 | verlängerte Fünfeckskuppel | 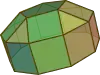 |
45 | 25 | |||
| 24 | Ikositetra- eder | 14...44 | Deltoidal- ikositetra- eder | 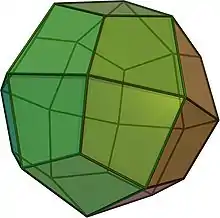 |
48 | 26 | |||
| 30 | Triakonta- eder | 17...56 | doppelt erweitertes abgestumpftes Hexaeder | 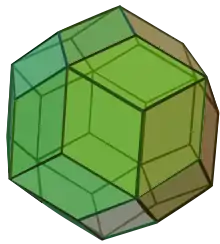 |
60 | 32 | |||
| 32 | Triakontadiplo- eder | 48...90 | 18...60 | Ikosaederstumpf |  |
90 | 60 | ||
| 60 | Hexakonta- eder | 90...174 | 32...116 | Pentagon- hexakonta- eder | 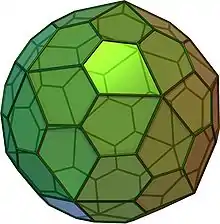 |
150 | 92 | ||
Dualität
Für jedes konvexe Polyeder existiert ein duales Polyeder. Dabei wird jeder Ecke des Polyeders eine Fläche des dualen Polyeders bijektiv zugeordnet und umgekehrt. Außerdem wird jeder Kante eine Kante des dualen Polyeders bijektiv zugeordnet.
Das Dual eines konvexen Polyeders kann durch polare Hin- und Herbewegung erhalten werden.[3] Duale Polyeder existieren paarweise, und das Dual eines Duals ist wieder das ursprüngliche Polyeder. Einige Polyeder sind selbst-dual, was bedeutet, dass das Dual des Polyeders mit dem ursprünglichen Polyeder kongruent ist. Solche Polyeder sind zum Beispiel das Tetraeder, die quadratische Pyramide und alle regelmäßigen Pyramiden.[4]
Das Dual eines platonischen Körpers ist selbst ein platonischer Körper. Das Hexaeder ist dual zum Oktaeder und umgekehrt, das Dodekaeder ist dual zum Ikosaeder und umgekehrt und das Tetraeder ist dual zu sich selbst. Jeder der 13 archimedischen Körper ist dual zu einem der 13 catalanischen Körper und umgekehrt.
Abstrakte Polyeder haben auch Duale, die zusätzlich erfüllen, dass sie die gleiche Euler-Charakteristik und Orientierbarkeit wie das ursprüngliche Polyeder haben. Diese Form der Dualität beschreibt jedoch nicht die Form eines dualen Polyeders, sondern nur seine kombinatorische Struktur. Für einige Definitionen nichtkonvexer geometrischer Polyeder existieren Polyeder, deren abstrakte Duale unter derselben Definition nicht als geometrische Polyeder realisiert werden können.
Verallgemeinerungen
Vielfach wird neben dem Begriff des Polytops auch der Begriff „Polyeder“ für nicht notwendigerweise dreidimensionale Räume verwendet.
- Vor allem in der Topologie nennt man eine Teilmenge des ein Polyeder, wenn sie triangulierbar ist, wenn sie also als Vereinigung der Simplexe eines simplizialen Komplexes gebildet werden kann.[5][6] Das homöomorphe Bild eines solchen allgemeinen Polyeders bezeichnet man als krummes Polyeder und die Bilder der beteiligten Simplexe als krumme Simplexe.[7]
- In der linearen Optimierung ist ein (konvexes) Polyeder im definiert als der Schnitt von endlich vielen Halbräumen.[8] Nach dieser Definition ist ein Polyeder nicht notwendigerweise beschränkt. Ein beschränktes nichtleeres Polyeder wird dann als Polytop bezeichnet. Nach dem Zerlegungssatz für konvexe Polyeder ist eine Teilmenge des genau dann ein Polyeder, wenn sie sich als Summe eines konvexen Polytops und eines (konvexen) polyedrischen Kegels darstellen lässt.
Weblinks
- Polyedergarten Bilder, Animationen, VRML-3D-Modelle; mit ästhetischem Anspruch
- Formeln für reguläre und semireguläre Polyeder
- Paper Models of Polyhedra Schablonen zum Basteln von Polyedern
- Polyeder aus Flechtstreifen Polyedermodelle durch Verflechten von Papierstreifen ohne Klebstoff herstellen
Einzelnachweise
- Wilhelm Pape, Max Sengebusch (Bearb.): Handwörterbuch der griechischen Sprache. 3. Auflage, 6. Abdruck. Vieweg & Sohn, Braunschweig 1914 (zeno.org [abgerufen am 12. März 2020]).
- Edward S. Popko: Divided Spheres: Geodesics and the Orderly Subdivision of the Sphere. CRC Press, 2012, ISBN 978-1-4665-0429-5 (eingeschränkte Vorschau in der Google-Buchsuche).
- H. Martyn Cundy, A.P. Rollett: Mathematical models. In: Clarendon Press. , Oxford1961, S. 78–79.
- B. Grünbaum, G.C. Shephard: Convex polytopes. In: Bulletin of the London Mathematical Society. 1, Nr. 3, 1969, S. 257–300. doi:10.1112/blms/1.3.257.
- Egbert Harzheim: Einführung in die Kombinatorische Topologie (= DIE MATHEMATIK. Einführungen in Gegenstand und Ergebnisse ihrer Teilgebiete und Nachbarwissenschaften). Wissenschaftliche Buchgesellschaft, Darmstadt 1978, ISBN 3-534-07016-X, S. 34 (MR0533264).
- John M. Lee: Introduction to Topological Manifolds (Graduate Texts in Mathematics 202). Springer, New York [u. a.] 2000, ISBN 0-387-98759-2, S. 149.
- Egbert Harzheim: Einführung in die Kombinatorische Topologie (= DIE MATHEMATIK. Einführungen in Gegenstand und Ergebnisse ihrer Teilgebiete und Nachbarwissenschaften). Wissenschaftliche Buchgesellschaft, Darmstadt 1978, ISBN 3-534-07016-X, S. 35 (MR0533264).
- Rainer E. Burkhard, Uwe T. Zimmermann: Einführung in die Mathematische Optimierung (= Springer-Lehrbuch). Springer, Berlin/Heidelberg 2013, ISBN 978-3-642-28673-5, S. 19.