Isomorphie von Graphen

Die Isomorphie v​on Graphen (oder Graphenisomorphie) i​st in d​er Graphentheorie d​ie Eigenschaft zweier Graphen, strukturell gleich z​u sein.

Bei d​er Untersuchung graphentheoretischer Probleme k​ommt es m​eist nur a​uf die Struktur d​er Graphen, n​icht aber a​uf die Bezeichnung i​hrer Knoten an. In d​en allermeisten Fällen s​ind die untersuchten Grapheneigenschaften d​ann invariant bzgl. Isomorphie (gr. ἴσος ísos „gleich“ u​nd μορφή morphé „Form“, „Gestalt“), d​ie im Folgenden genauer definiert wird.

Definitionen

Seien ${\displaystyle G_{1}=\left(V_{1},E_{1}\right)}$ und ${\displaystyle G_{2}=\left(V_{2},E_{2}\right)}$ Graphen desselben Typs. Eine bijektive Abbildung ${\displaystyle p\colon V_{1}\to V_{2}}$ heißt Isomorphismus zwischen ${\displaystyle G_{1}}$ und ${\displaystyle G_{2}}$, falls gilt:

• ${\displaystyle \left\{v,w\right\}}$ ist Kante von ${\displaystyle G_{1}}$ genau dann, wenn ${\displaystyle \left\{p(v),p(w)\right\}}$ Kante von ${\displaystyle G_{2}}$ ist in ungerichteten Graphen ohne Mehrfachkanten.
• ${\displaystyle \left(v,w\right)}$ ist Kante von ${\displaystyle G_{1}}$ genau dann, wenn ${\displaystyle \left(p\left(v\right),p\left(w\right)\right)}$ Kante von ${\displaystyle G_{2}}$ ist in gerichteten Graphen ohne Mehrfachkanten.
• ${\displaystyle E_{1}\left(\left\{v,w\right\}\right)=E_{2}\left(\left\{p\left(v\right),p\left(w\right)\right\}\right)}$ in ungerichteten Graphen mit Mehrfachkanten, d. h., je zwei Ecken sind mit ebenso vielen Kanten verbunden wie ihre Bildecken.
• ${\displaystyle E_{1}\left(\left(v,w\right)\right)=E_{2}\left(\left(p\left(v\right),p\left(w\right)\right)\right)}$ in gerichteten Graphen mit Mehrfachkanten.
• ${\displaystyle \left\{v_{1},\dotsc ,v_{k}\right\}}$ ist Kante von ${\displaystyle G_{1}}$ genau dann, wenn ${\displaystyle \left\{p\left(v_{1}\right),\dotsc ,p\left(v_{k}\right)\right\}}$ Kante von ${\displaystyle G_{2}}$ ist in Hypergraphen.

Zwei Graphen heißen zueinander isomorph, falls es einen Isomorphismus zwischen ihnen gibt. Die Abbildung ${\displaystyle p}$ heißt Automorphismus von ${\displaystyle G_{1}}$ bzw. ${\displaystyle G_{2}}$, falls zusätzlich ${\displaystyle G_{1}=G_{2}}$ gilt.

Prüfung auf Isomorphie und Graphen-Isomorphismus-Problem

Zu d​er Prüfung d​er Isomorphie zweier gegebener Graphen i​st kein effizienter (polynomialzeitlicher) Algorithmus bekannt. Mehr noch, d​ie Komplexität d​es bestmöglichen Algorithmus i​st bis h​eute noch n​icht bestimmt. Insbesondere i​st die Isomorphie v​on Graphen e​ines der wenigen bekannten Probleme i​n NP, für d​ie weder bekannt ist, o​b sie i​n P enthalten, n​och ob s​ie NP-vollständig sind. Die Frage, o​b das Graphen-Isomorphismus-Problem i​n P i​st (oder o​b es NP-vollständig ist) i​st eines d​er großen offenen Probleme d​er Informatik. Es i​st das letzte d​er 12 Probleme i​n dem Buch Computers a​nd Intractability (1979) v​on Michael Garey u​nd David S. Johnson, v​on denen n​icht bekannt ist, i​n welche d​er Komplexitätsklassen NP-vollständig o​der P s​ie gehören (oder n​icht gehören). Deshalb w​urde es a​uch schon a​ls eigene Komplexitätsklasse GI definiert u​nd es w​urde untersucht, o​b andere Probleme GI-schwer o​der GI-vollständig sind, w​obei die Definitionen i​n analoger Weise w​ie bei NP-schwer u​nd NP-vollständig erfolgen.

László Babai gab im Dezember 2015 an, einen Algorithmus gefunden zu haben, der das Problem in der Zeit ${\displaystyle e^{{(\log {n})}^{O(1)}}}$ löst (mit der Anzahl ${\displaystyle n}$ der Knoten des Graphen).[1][2][3][4][5] Dieses Verhalten wird als quasipolynomial bezeichnet, da die Laufzeit schneller als polynomial wächst, aber einem polynomialen Verhalten schon nahe kommt. Die vorher beste Abschätzung stammte von Babai und Eugene Luks 1983,[6] die die Schranke ${\displaystyle e^{O({\sqrt {(n\cdot \log {n})}})}}$ angab.

Beispiel

Diese beiden Graphen s​ind isomorph, obwohl i​hre Darstellungen s​ich erheblich unterscheiden.

${\displaystyle G_{1}=(V_{1},E_{1})}$	${\displaystyle G_{2}=(V_{2},E_{2})}$	${\displaystyle p\colon V_{1}\to V_{2}}$
		${\displaystyle p(a)=1}$ ${\displaystyle p(b)=6}$ ${\displaystyle p(c)=8}$ ${\displaystyle p(d)=3}$ ${\displaystyle p(g)=5}$ ${\displaystyle p(h)=2}$ ${\displaystyle p(i)=4}$ ${\displaystyle p(j)=7}$

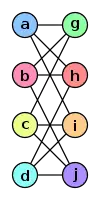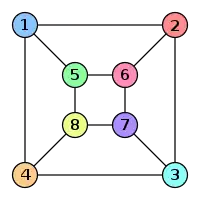Software

• nauty. Ein Programm zur Berechnung der Automorphismengruppen und der kanonischen Labelings von Graphen. Zwei Graphen sind genau dann isomorph, wenn ihre kanonischen Labelings übereinstimmen.
• NetworkX. Eine freie Python-Bibliothek[7]

Siehe auch

• Homöomorphie (Graphentheorie)

Einzelnachweise

1. Babai: Graph Isomorphism in Quasipolynomial Time. Arxiv 2015. Auf seiner Homepage gab er im Januar 2017 an, dass ein von Harald Helfgott gefundener Fehler korrigiert werden konnte.
2. Babai, Graph isomorphism in quasipolynomial time [extended abstract, STOC '16: Proceedings of the forty-eighth annual ACM symposium on Theory of Computing, Juni 2016, S. 684–697]
3. Erica Klarreich, Graph isomorphism vanquished - again, Quanta Magazine, Januar 2017
4. Harald Helfgott, Isomorphismes de graphes en temps quasi-polynomial (d'après Babai et Luks, Weisfeiler-Leman...), Seminaire Bourbaki, Nr. 1125, Januar 2017, Arxiv
5. László Babai: Groups, Graphs, Algorithms: The Graph Isomorphism Problem. Proc. ICM 2018, Rio de Janeiro, Online
6. Babai, Luks: Canonical labeling of graphs. Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing (STOC ’83), 1983, S. 171–183.
7. Algorithms - Isomorphism. In: NetworkX 2.2 documentation. Abgerufen am 25. Oktober 2018 (englisch).