Dichteste Kugelpackung
Die dichteste Kugelpackung ist diejenige gegenseitige Anordnung gleich großer Kugeln, die den kleinsten Raum beansprucht. Der leere Raum zwischen den dichtest gepackten Kugeln nimmt nur etwa 26 % des Gesamtraumes ein, bzw. die Packungsdichte beträgt etwa 74 %[1][2]:
- .

jede horizontale Schicht ist wie in der
1. Beschreibung belegt;
die Schichten folgen aufeinander nach dem Schema ABAB... (s. unten)

jede horizontale Schicht ist wie in der
2. Beschreibung belegt;
die als Schichten angesehenen Seitenwände folgen aufeinander ins Innere der Pyramide hinein nach dem Schema ABCABC... (s. unten)

Diese Anordnung kann auf zweierlei Art beschrieben werden:
Sie besteht aus ebenen Schichten aus sich berührenden Kugeln,
- von denen jede von sechs benachbarten Kugeln und von je drei Kugeln aus der Schicht darüber und aus der darunter berührt wird,[3] oder
- von denen jede von vier benachbarten Kugeln und von je vier Kugeln aus der Schicht darüber und aus der darunter berührt wird.
Übereinstimmend heißt es, dass jede Kugel von 12 anderen berührt wird (Kusszahl = 12). Die erste (1.) der beiden Beschreibungen ist die bevorzugt gebrauchte. Die darin enthaltene Schicht wird als hexagonale (regelmäßig sechseckige) Kugel-Schicht, die im zweiten Fall als tetragonale (quadratische) Kugel-Schicht bezeichnet.
Das Problem geht auf Sir Walter Raleigh zurück, der die Frage stellte, wie Kanonenkugeln in[4] einem Schiff am dichtesten gestapelt werden könnten (siehe auch nebenstehendes Bild). 1611 äußerte Johannes Kepler die Vermutung, dass dichteste Kugelpackungen in kubisch-flächenzentrierten und in hexagonalen Kristallsystemen vorlägen. Carl Friedrich Gauß bewies 1831 die Richtigkeit dieser Vermutung.[5] 1998 legte der amerikanische Mathematiker Thomas Hales einen Computerbeweis vor, dass diese beiden Anordnungen die einzigen mit dichtester Kugelpackung sind. Wie alle Computerbeweise wird auch diese Arbeit in Teilen der mathematischen Fachwelt noch nicht anerkannt.
Unter dichtester Kugelpackung wird die Packungsdichte in einer Anordnung von unendlich vielen Kugeln verstanden. Endlich viele Kugeln weisen deren Wert auch auf, wenn die äußeren Kugeln nur zum Teil mitgezählt werden. Die Grenze des betrachteten Bruttoraumes führt durch die Mittelpunkte dieser Kugeln. In der Theorie der endlichen Kugelpackungen ist der Bruttoraum größer. Die ihn bildende Hülle (z. B. ein Sack für kugelförmige Güter) enthält die äußeren Kugeln in Gänze.
Schichtfolgen
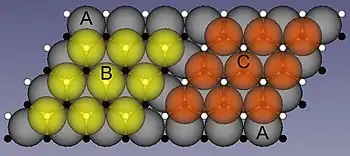
gelb und rot: B-Schicht oder C-Schicht (hier als zweite Schicht; allgemein in beliebiger Reihenfolge als zweite oder dritte Schicht)
Hexagonale Schichten
In einer hexagonalen Kugelschicht ist jede Kugel außer von 6 Kugeln auch von 6 Lücken umgeben. Eine auf eine erste Kugelschicht A (s. nebenstehende Abbildung) gelegte zweite Kugelschicht benötigt 3 der 6 Lücken zum "Einrasten". Dabei bestehen zwei Möglichkeiten: Einrasten in die weiß markierten oder in die schwarz markierten Lücken in der Schicht A. In einem Fall (weiße Lücken) wird die aufgelegte Schicht als eine B-Schicht, im anderen Fall (schwarze Lücken) als eine C-Schicht bezeichnet (Bezeichnungen A, B und C sind die in der Kristallographie üblichen). Die dritte Kugelschicht hat zum Einrasten in die zweite wiederum zwei Möglichkeiten: Rastet sie so ein, dass sie über der untersten Schicht zu liegen kommt, wird sie wie diese als eine A-Schicht bezeichnet. Wenn sie die zweite Möglichkeit des Einrastens nutzt, nimmt sie eine dritte Lage ein und wird als eine C-Schicht bezeichnet.

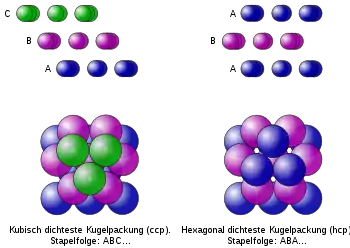
Kubisch dichteste Kugelpackung (ccp) (links)
Hexagonal dichteste Kugelpackung (hcp) (rechts)
unten: Draufsicht;
oben: streifende Ansicht der Kugelreihen in den drei Schichten (Kugeln verkleinert, Ansicht entspricht der von links oder rechts in obiger Abbildung)
Die Stapelfolge ist prinzipiell unendlich vielfältig. Praktische Bedeutung (Kristallographie) haben aber fast ausschließlich nur die sich nach zwei bzw. drei verschiedenen Schichtlagen fortwährend wiederholenden Stapel. Sie werden als Schichtlagenfolgen ABAB... bzw. ABCABC... bezeichnet. Die Schichtenfolge ABAB... ist das Ergebnis davon, dass grundsätzlich erst die übernächste (dritte) hexagonale Kugelschicht fluchtend über der ersten liegen kann. Die Schichtenfolge ABCABC... folgt der Tatsache, dass, wenn nicht die übernächste (dritte) über der ersten Schicht fluchtend liegt, so aber die über-übernächste (vierte) Schicht fluchtend über der ersten liegen muss.[6] Abgesehen davon kann das Stapeln in beliebiger Lege-Reihenfolge fortgesetzt sein; die Schichten müssen nur gegenseitig „einrasten“, damit der Wert der Packungsdichte ≈ 74,05 % ist.
Quadratische Schichten
In quadratischen Schichten ist jede Kugel von vier Lücken umgeben. Da eine aufgelegte Schicht alle vier Lücken zum Einrasten benötigt, gibt es nur einen einzigen Schichtfolgen-Typ und auch nur die kubisch-flächenzentrierte Elementarzelle, aus denen der Stapelaufbau ebenfalls vorstellbar ist. Eine dieser Elementarzellen erstreckt sich über drei kubisch-flächenzentrierte Elementarzellen.
Die oben abgebildete Pyramide aus Kanonenkugeln mit rechteckigem Grundriss ist eine Stapelfolge quadratischer Kugelschichten. In der Kristallographie wird nicht mit quadratischen Schichten gearbeitet, denn schräg durch einen Stapel aus hexagonalen Kugelschichten mit der Schichtfolge ABCA erstrecken sich quadratische Schichten, in denen die kubisch-flächenzentrierte Elementarzelle erkennbar ist.[7]
Naturwissenschaftliche Bedeutung
Die Anordnung von Atomen in einer dichtesten Kugelpackung entspricht einem wichtigen Grundprinzip bei der Bildung von Kristallen: Bei der Zusammensetzung der Materie aus ihren kleinsten Teilen (Atome, Moleküle und größere) gilt das Prinzip der Minimierung des Volumens. Die kleinsten Teile bilden zusammen dichteste Kugelpackungen. Dabei spricht man auch dann von einer dichtesten Kugelpackung, wenn die Teilchen nicht exakt auf den theoretisch vorgegebenen Positionen liegen. Enthaltene kleine Baufehler werden Stapelfehler genannt.
Einatomige Systeme
Dabei handelt es sich um die in Kristallform existierenden reinen Metalle.
Die hexagonal dichteste Kugelpackung (hcp, Schichtfolge ABABAB...) wird auch Magnesium-Typ genannt. Es kristallisieren Beryllium, Magnesium, die Elemente der Gruppe 3 (Scandium, Yttrium, Lanthan) und die Gruppe 4 (Titan, Zirconium, Hafnium), Technetium, Rhenium, Ruthenium, Cobalt, Zink, Cadmium und Thallium in diesem Strukturtyp.
Die kubisch dichteste Kugelpackung (ccp, Schichtfolge ABCABC...) Kupfer-Typ genannt. Neben Kupfer kristallisieren Calcium, Strontium, Nickel, Rhodium, Iridium, Palladium, Platin, Silber, Gold, Aluminium und Blei in diesem Strukturtyp.
Insbesondere die leichteren Lanthanoiden und schwerere Actinoiden liegen bei Standardbedingungen in einer Mischform vor (Schichtfolge ABACABAC...). Diese hat dieselbe Raumgruppe wie die hcp-Struktur, aber mit vier Atomen in der Elementarzelle, und zwar auf (0,0,0) / (0,0,1/2) (Wyckoff-Position 2a) und (1/3,2/3,3/4) / (2/3,1/3,1/4) (Wyckoff-Position 2d). Sie wird daher auch double hexagonal closest packed (dhcp)-Struktur genannt. Praseodym oder Curium sind Elemente, die in diesem Strukturtyp kristallisieren.
Mehratomige Systeme
Viele Kristallstrukturen mit überwiegend ionischem Bindungstyp beruhen auf einer dichtesten Kugelpackung eines Teils der Ionen und der Einlagerung der anderen Ionen in den Lücken. Sind diese Einlagerungsionen zu groß für die Lücke, wird die Kugelpackung entsprechend deformiert. Die Art und das Ausmaß dieser Deformation hängen dabei von dem Größenverhältnis der Gerüstionen zu den Einlagerungsionen ab. Für einige Stöchiometrien gibt es Beziehungen um aus den Ionenradien sogenannte Toleranzfaktoren zu berechnen. Anhand dieser Toleranzfaktoren kann man Vorhersagen über die Struktur und Verhalten des jeweiligen Systems ableiten. Ein bekanntes Beispiel dafür ist die Perowskit-Struktur.
Polytype
Als Polytype werden Kristalle bezeichnet, die eine Stapelfolge mit langer Wiederholungseinheit besitzen. Beispiele dafür sind Zinksulfid (ZnS) mit mehr als 150 polytypen Formen und Siliciumcarbid (SiC). Diese Polytype verfügen zum Teil über extrem große Gitterkonstanten. So hat das Polytyp von SiC mit der Bezeichnung 393R die Gitterkonstanten a = 3,079 Å und c = 989,6 Å.
Nicht-Dichteste Kugelpackungen
Die kubisch innenzentrierte Kugelpackung (b.c.c., body-centered cubic) besteht aus zwei sich wiederholenden Schichten mit der Schichtfolge ABA... Das Koordinationspolyeder um die Atome ist ein Würfel (CN 8) und in etwas weiterer Entfernung ein weiteres Oktaeder (CN=6), so dass insgesamt die Koordinationszahl 8+6 folgt. Damit wird eine Raumerfüllung von 68,02 % erreicht. Dieser Strukturtyp hat die Nummer A2 in den Strukturberichten und wird auch Wolfram-Typ genannt. Es kristallisieren die Alkalimetalle, Barium, die Elemente der Gruppe 5 (Vanadium, Niob, Tantal) und Gruppe 6 (Chrom, Molybdän, Wolfram) und Eisen in diesem Strukturtyp.
Die Elemente Mangan, Quecksilber, Gallium, Germanium, Indium, Zinn, Antimon und Bismut kristallisieren in einem eigenen Strukturtyp.
Die regellos dichteste Packung (dichteste Zufallspackung, engl. random close pack) ist die empirisch gefundene dichteste Packung von zufällig gepackten Kugeln mit einer Raumerfüllung von circa 64 %.
Packungen in anderen als drei Dimensionen
In zwei Dimensionen bewies Joseph-Louis Lagrange 1773, dass die hexagonale Anordnung die dichteste Kugelpackung mit Kugeln auf einem Gitter ist. Lässt man auch andere als Gitterpackungen zu, bewies dies Axel Thue 1910 (vervollständigt durch László Fejes Tóth, Kurt Mahler, Beniamino Segre 1940).[8]
Der dreidimensionale Fall ist die inzwischen bewiesene Kepler-Vermutung (wobei den Fall von Gitterpackungen schon Carl Friedrich Gauß 1831 löste).
In höheren Dimensionen ist das Problem weitgehend offen. Die dichtesten Gitterpackungen sind bis zur Dimension d=8 im euklidischen Raum bekannt.[9] Dabei bestimmten Alexander Nikolajewitsch Korkin und Jegor Iwanowitsch Solotarjow[10][11] die dichtesten Gitterpackungen in den Dimensionen 4 und 5 und Hans Blichfeldt 1934 die Dimensionen 6, 7 und 8. Darüber hinaus ist fast nichts sicher bekannt. Das berühmte Leech-Gitter in 24 Dimensionen und das E8-Gitter (benannt nach der exzeptionellen Liegruppe E8, dessen Wurzelsystem es ist) in acht Dimensionen wurden häufig als dichteste Kugelpackung vermutet, insbesondere nach Entwicklung neuer oberer Schranken für dichteste Kugelpackungen durch Noam Elkies und Henry Cohn (2003), und 2016 kündigte Maryna Viazovska einen Beweis an. Dichte Kugelpackungen in höheren Dimensionen haben große Bedeutung für die Kodierungstheorie (fehlerkorrigierende Codes).
Weblinks
- Unterrichtsmaterial zum Thema dichteste Kugelpackung von der IUCr
- Animation einer kubisch dichtesten Kugelpackung (SWF-Datei; 391 kB)
- Anzahl der dichtesten reguläre Kugelpackungen im Raum und Erklärung der Sm-Kristallstruktur
- Darstellung der hexagonalen und kubischen Kugelpackungen
- Weitz / HAW Hamburg: Die Keplersche Vermutung (Weihnachtsvorlesung 2019)
Literatur
- Ch. Kittel: Einführung in die Festkörperphysik. 10. Auflage. Oldenbourg Verlag, München 1993, ISBN 3-486-22716-5.
- George G. Szpiro: Die Keplersche Vermutung. Wie Mathematiker ein 400 Jahre altes Rätsel lösten. Springer, Heidelberg [u. a.] 2011, ISBN 978-3-642-12740-3.
- Catherine E. Houscraft, Alan G. Sharpe: Anorganische Chemie. 2. Auflage. Pearson Studium, München 2006, ISBN 3-8273-7192-9.
Einzelnachweise
- te:c-science.com: gemeinsame Herleitung der Packungsdichte für kubisch-flächenzentriertes und hexagonal dichtest gepacktes Gitter, gemeinsam
- Siegfried Wetzel: Dichteste Kugelpackung; 8. Die kristallographischen Elementarzellen und ihre Packungsdichten; getrennte Berechnung für kubisch-flächenzentrierte und hexagonale Elementarzelle
- Tóth, László Fejes: Dichteste Kugelpackung, Abhandlungen der Braunschweigischen Wissenschaftlichen Gesellschaft Band 27, 1977, S. 319
- Siegfried Wetzel: Dichteste Kugelpackung; 2. Schichtweises Errichten von Pyramiden aus Kanonen- oder anderen Kugeln, ff
- Gauß, Untersuchungen über die Eigenschaften der positiven ternären quadratischen Formen von Ludwig August Seber, Göttingesche Gelehrte Anzeigen, 9. Juli 1831, Journal für Reine und Angewandte Mathematik, Band 20, 1840, S. 312–320, Gauß, Werke, Göttinger Akademie der Wissenschaften Band 2, 1876, S. 188–196
- Siegfried Wetzel: Dichteste Kugelpackung; 9. ABA und ABCA – in der Kristallographie gebrauchte Kürzel beim Stapeln hexagonaler Kugelschichten
- Siegfried Wetzel: Dichteste Kugelpackung; 6. Die kubisch-flächenzentrierte Elementarzelle
- Jörg Wills, Kugelpackungen - Altes und Neues, Mitteilungen DMV, 1995, Nr. 4.
- Wolfram Mathworld: Hypersphere Packing.
- Eric Weisstein, Hypersphere Packings
- Korkin, Zolotarev: Sur les formes quadratiques positives. Math. Ann., Band 11, 1877, S. 242–292.