Hexagonales Kristallsystem

Das hexagonale Kristallsystem gehört zu den sieben Kristallsystemen der Kristallographie. Es umfasst alle Punktgruppen mit einer sechszähligen Dreh- oder Drehinversionsachse. Das hexagonale Kristallsystem ist mit dem trigonalen Kristallsystem eng verwandt und bildet zusammen mit ihm die hexagonale Kristallfamilie.

Die hexagonalen Punktgruppen

Das hexagonale Kristallsystem umfasst die Punktgruppen $6,\,{\bar {6}},\,6/m,\,622,\,6mm,\,{\bar {6}}m2$ und $\ 6/mmm$ . Dies sind alle die Punktgruppen der hexagonalen Kristallfamilie, in denen es keine Raumgruppe mit rhomboedrischer Zentrierung gibt. Die Raumgruppen des hexagonalen Kristallsystems können alle mit dem hexagonal primitiven Achsensystem beschrieben werden. Die hexagonalen Punktgruppen haben keine kubische Obergruppe. Somit ist die hexagonale Holoedrie zusammen mit der kubischen die höchstsymmetrische kristallographische Punktgruppe.

Das hexagonale Achsensystem

Bild 1: die hexagonale Elementarzelle

Bild 2: hexagonale Zelle

In der hexagonalen Kristallfamilie gibt es das hexagonale und das trigonale Kristallsystem, sowie das hexagonale und das rhomboedrische Gitter-System. Die Einteilung in Kristallsysteme beruht auf der Symmetrie der Kristalle, die Einteilung in Gittersysteme bezieht sich auf die Metrik des Gitters. Während in den fünf anderen Kristallfamilien bzw. Kristallsystemen diese unterschiedlichen Sichtweisen zur selben Einteilung führen, ist dies in der hexagonalen Kristallfamilie nicht so. Darüber hinaus erfolgt hier die Einteilung in Gittersysteme nicht auf Basis der Punktgruppen, sondern der Raumgruppen. Da die Verhältnisse relativ kompliziert sind, werden sie an dieser Stelle ausführlicher beschrieben.

Das hexagonale Achsensystem in der Kristallographie

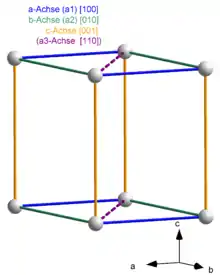
Wie in allen wirteligen Kristallsystemen wird die Drehachse mit der höchsten Zähligkeit in die Richtung der c-Gitterachse gelegt. Die Ebene senkrecht dazu wird durch zwei gleich lange Achsen a₁ und a₂ beschrieben, die im Winkel von 120° zueinander stehen. Daraus ergibt sich folgende Metrik: $a=b\neq c$ und $\alpha =\beta =90^{\circ },\,\gamma =120^{\circ }.$ Die durch diese Basisvektoren gebildete Elementarzelle ist in Bild 1 dargestellt. Sie hat ein Volumen von $V=a^{2}c\sin 60^{\circ }={\tfrac {\sqrt {3}}{2}}a^{2}c.$

Das hexagonale Achsensystem in anderen Fachrichtungen

In der Mineralogie und besonders in der Metallkunde ist es üblich, noch eine zusätzliche Achse a₃ in der (a₁, a₂) Ebene zu verwenden (vgl. Bild 3). Diese hat dieselbe Länge wie a₁ und steht im Winkel zu 120° sowohl zu a₁ als auch zu a₂. Die Millerschen Indizes werden um den Index i zu so genannten Miller-Bravais-Indizes erweitert und haben dann vier Komponenten: (h, k, i, l). Dabei ist der Index i redundant, da gilt: i = -(h+k). Ähnlich werden in der Metallkunde auch Richtungen durch viergliedrige Symbole [uvtw], die Weber-Indizes, dargestellt.

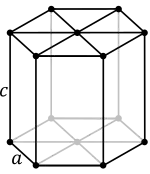
Oft wird in der Literatur die hexagonale Zelle als sechseckiges Prisma dargestellt (vgl. Bild 2). Da dieses Prisma kein Parallelepiped ist, handelt es sich aber nicht um eine Elementarzelle. Dieses Prisma besteht aus drei hexagonalen Elementarzellen.

Die a₁-a₂-Ebene

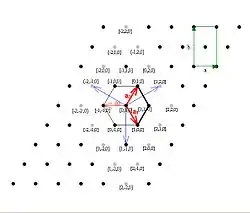
Bild 3: Die a₁-a₂-Ebene des hexagonalen Achsensystems

Bild 3 stellt die a₁-a₂-Ebene des hexagonalen Achsensystems dar. Im Einzelnen:

Punkte: Gitterpunkte des hexagonalen Achsensystems in der a₁-a₂-Ebene zum Teil mit Koordinaten x,y,0.
Graue Punkte: Punkte mit einem Index ± 2.
Fette Linien: die Grundfläche der hexagonalen Elementarzelle.
Schwarze Linien: die Grundfläche des sechseckigen Prismas, das oft zur Veranschaulichung des hexagonalen Gittersystems verwendet wird.
Rote Pfeile: die Gittervektoren des hexagonalen Gitters, dünn: die in der Mineralogie übliche 3. a-Achse.
Blaue Pfeile: Blickrichtung des 3. Raumgruppensymbols nach Hermann-Mauguin entsprechend den International Tables for Crystallography 3. Auflage.
Grün: Grundfläche der orthohexagonalen Zelle. (Siehe unten)
Grüne Pfeile: Gittervektoren der orthohexagonalen Zelle. (Der 3. Gittervektor ist der hexagonale c-Vektor)

Die rhomboedrische Zentrierung

Bei der Betrachtung möglicher Zentrierungen kommt es in diesem Achsensystem zu einer Besonderheit. Fügt man zusätzliche Gitterpunkte so ein, dass die volle Symmetrie des hexagonalen Gitters erhalten bleibt, so ergeben sich nur Punktgitter, die auch durch ein primitives hexagonales Gitter (mit anderen Gitterkonstanten) beschrieben werden können.

Fügt man aber zusätzliche Gitterpunkte an den Stellen $({\tfrac {2}{3}},\,{\tfrac {1}{3}},\,{\tfrac {1}{3}})$ und $({\tfrac {1}{3}},\,{\tfrac {2}{3}},\,{\tfrac {2}{3}})$ beziehungsweise $({\tfrac {1}{3}},\,{\tfrac {2}{3}},\,{\tfrac {1}{3}})$ und $({\tfrac {2}{3}},\,{\tfrac {1}{3}},\,{\tfrac {2}{3}})$ ein, so ergibt sich ein neues Gitter, das aber nicht mehr die volle Symmetrie des hexagonalen Punktgitters, sondern die niedrigere Symmetrie ${\bar {3}}m$ hat.

Dieses Gittersystem kann auch mit einer primitiven Elementarzelle beschrieben werden. Für die Metrik dieser Zelle gilt: $a=b=c$ und $\alpha =\beta =\gamma \neq 90^{\circ }$ . Diese Elementarzelle hat die Form eines Rhomboeders, eines entlang seiner Raumdiagonalen verzerrten Würfels. Diese Elementarzelle ist zwar primitiv, aber nicht konventionell, da die dreizählige Achse nicht in Richtung eines Gittervektors, sondern in Richtung der Raumdiagonalen liegt. Dieses Gittersystem wird rhomboedrisch genannt, hat die Holoedrie ${\bar {3}}m$ und wird unabhängig von der Aufstellung (hexagonale oder rhomboedrische Achsen) als R-Gitter bezeichnet.

Die Lage der rhomboedrischen zu den hexagonalen Achsen hängt davon ab, welche der beiden Möglichkeiten zur Zentrierung der hexagonalen Zelle verwendet wurde. Im ersten Fall heißt die Aufstellung der Achsen obvers, im zweiten Fall revers. In der ersten Ausgabe der International Tables von 1935 wurde die reverse Aufstellung verwendet, in den darauffolgenden die obverse. Der Unterschied zwischen beiden Aufstellungen besteht in einer Drehung der hexagonalen zu den rhomboedrischen Achsen um 60°, 180° oder 300°.

Da dieses Gittersystem nicht die volle Symmetrie des hexagonalen hat, kommt es nicht in allen Punktgruppen der hexagonalen Kristallfamilie vor.

Verwendung im trigonalen und hexagonalen Kristallsystem

Das hexagonale Achsensystem wird zur Beschreibung aller Punktgruppen der hexagonalen Kristallfamilie eingesetzt. Punktgruppen deren Raumgruppen ausschließlich mit dem primitiv hexagonalen Gitter beschrieben werden können, bilden das hexagonale Kristallsystem. Alle Punktgruppen, in denen auch das rhomboedrisch zentrierte Gitter vorkommt, bilden das trigonale Kristallsystem. Auch in diesem System werden alle nicht zentrischen Raumgruppen mit dem hexagonalen Achsensystem beschrieben. Eine Beschreibung dieser Raumgruppen mit dem rhomboedrischen Gittersystem ist nicht möglich, auch wenn sie zur Holoedrie des rhomboedrischen Gittersystems gezählt werden. Nur bei den zentrischen Raumgruppen (Symbol R) hat man die Auswahl zwischen dem hexagonalen und dem rhomboedrischen Achsensystem.

Rhomboedrische oder hexagonale Achsen

Im Gegensatz zur rhomboedrischen Zelle ist die hexagonale Zelle eine konventionelle Zelle, daher wird in der Regel das hexagonale Achsensystem verwendet. Bei den Strukturdaten der Minerale spielt das rhomboedrische System nur eine untergeordnete Rolle.

Das Rhomboeder ist ein in Richtung der Raumdiagonalen verzerrter Würfel. Daher ist der Einsatz dieser Aufstellung in den Fällen angebracht, in denen eine kubische und eine rhomboedrische Struktur miteinander verglichen werden, da man hierbei das Achsensystem nicht ändern muss.

Das orthohexagonale System

Da das hexagonale Achsensystem kein orthogonales System ist, ist seine Metrik komplizierter. Einer der Ansätze damit umzugehen ist die Beschreibung durch ein orthorhombisches Gittersystem, das sogenannte orthohexagonale System. Es handelt sich dabei um eine orthorhombisch C-zentrierte Zelle. Die Grundfläche dieses Systems ist ein Rechteck mit dem Seitenlängenverhältnis b:a von ${\sqrt {3}}\approx 1{,}732$ . Sie ist in Bild 3 grün eingezeichnet. Die dritte Achse entspricht der hexagonalen c-Achse.

Der Vorteil dieser Aufstellung ist die einfachere Metrik, der Nachteil ist der Verlust einer expliziten drei- bzw. sechszähligen Achse.

Weitere zentrierte Zellen

Bei der Beschreibung von Ober- beziehungsweise Untergruppen wird in den International Tables eine dreifach vergrößerte hexagonale Zelle, die sogenannte H-Zelle verwendet.

Es ist auch möglich das hexagonale Gitter mit sechs zentrierten rhomboedrischen Zellen zu beschreiben. Diese Zellen werden D-Zellen genannt. Zur Beschreibung von Strukturen werden sie nicht verwendet.

Historische Anmerkungen

Die Einteilung der Kristalle in Kristallsysteme beruhte ursprünglich auf der Morphologie. Im trigonalen bzw. hexagonalen System wurden alle die Kristalle zusammengefasst, deren Kristallform auf das Vorhandensein einer drei- bzw. sechszähligen Drehachse schließen lässt. Da aber die sechszählige Drehinversionsachse eine dreizählige Kristallform bewirkt, wurden die Punktgruppen ${\bar {6}}$ (trigonal-dipyramidal) und ${\bar {6}}m2$ (ditrigonal-dipyramidal) anfangs zum trigonalen Kristallsystem gezählt, wie man an den Bezeichnungen für die Kristallformen heute noch sieht.

Punktgruppen im hexagonalen Kristallsystem und ihre physikalischen Eigenschaften

Zur Beschreibung der hexagonalen Kristallklassen in Hermann-Mauguin-Symbolik werden die Symmetrieoperationen bezüglich vorgegebener Richtungen im Gitter-System angegeben.

Im hexagonalen Achsensystem: 1. Symbol in Richtung der c-Achse (<001>). 2. Symbol in Richtung einer a-Achse (<100>). 3.Symbol in einer Richtung senkrecht zu einer a und der c-Achse (<120>). Für die 3. Richtung wird auch oftmals die im Allgemeinen nicht äquivalente Richtung <210> angegeben. Auch wenn dies speziell für die Angabe der Lage der Symmetrieelemente keine Rolle spielt, so entspricht diese Angabe nicht den Konventionen.

Charakteristisch für alle Raumgruppen des hexagonalen Kristallsystems ist die 6 (oder 6) an 1. Stelle des Raumgruppensymbols.

Punktgruppe (Kristallklasse)								Physikalische Eigenschaften[Anm. 1]				Beispiele
Nr.	Kristallsystem	Name	Schoenflies-Symbol	Internationales Symbol (Hermann-Mauguin)		Laueklasse	Zugehörige Raumgruppen (Nr.)	Enantiomorphie	Optische Aktivität	Pyroelektrizität	Piezoelektrizität; SHG-Effekt
Nr.	Kristallsystem	Name	Schoenflies-Symbol	Voll	Kurz	Laueklasse	Zugehörige Raumgruppen (Nr.)	Enantiomorphie	Optische Aktivität	Pyroelektrizität	Piezoelektrizität; SHG-Effekt
21	hexagonal	hexagonal-pyramidal	C₆	6	6	6/m	168–173	+	+	+ [001]	+	Nephelin Zinkenit
22		trigonal-dipyramidal	C_3h	6	6		174	–	–	–	+	Penfieldit Laurelit
23		hexagonal-dipyramidal	C_6h	6/m	6/m		175–176	–	–	–	–	Apatit Zemannit
24		hexagonal-trapezoedrisch	D₆	622	622	6/mmm	177–182	+	+	–	+	Hochquarz Pseudorutil
25		dihexagonal-pyramidal	C_6v	6mm	6mm		183–186	–	–	+ [001]	+	Wurtzit Zinkit
26		ditrigonal-dipyramidal	D_3h	6m2 bzw. 62m	6m2		187–190	–	–	–	+	Bastnäsit Benitoit
27		dihexagonal-dipyramidal	D_6h	6/m2/m2/m	6/mmm		191–194	–	–	–	–	Graphit Magnesium
Bei den Angaben zu den physikalischen Eigenschaften bedeutet „−“ aufgrund der Symmetrie verboten und „+“ erlaubt. Über die Größenordnung der optischen Aktivität, Pyro- und Piezoelektrizität sowie des SHG-Effekts kann rein aufgrund der Symmetrie keine Aussage getroffen werden. Man kann aber davon ausgehen, dass stets eine zumindest schwache Ausprägung der Eigenschaft vorhanden ist. Für die Pyroelektrizität ist, sofern vorhanden, auch die Richtung des pyroelektrischen Vektors angegeben.

Weitere hexagonal kristallisierende chemische Stoffe siehe Kategorie:Hexagonales Kristallsystem

Hexagonale Kristallformen

Bildbeispiele hexagonaler Kristallformen
hexagonale Dipyramide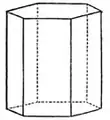
hexagonales Prisma
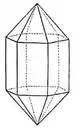Kombination Prisma – Pyramide
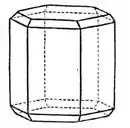Kombination Prisma mit pyramidaler Basis
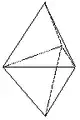trigonale Dipyramide (Kristallklasse 6)

Die hexagonal dichteste Kugelpackung

Hexagonal-dichteste Packung

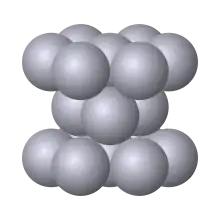
Die hexagonal dichteste Kugelpackung (hdp, engl. hcp) ist eine der zwei Möglichkeiten dichtester Kugelpackungen. Sie kann wie folgt beschrieben werden: Ihre Grundzelle ist ein sechsseitiges Prisma, dessen 12 Ecken mit je einer gleich großen Kugel besetzt sind. Der Kugeldurchmesser ist gleich der Kantenlänge (die 6 je Kugeln berühren sich). In der Mitte der je 6 Kugeln befindet sich je eine 7. Kugel gleichen Durchmessers. Die Höhe des Prismas ist so, dass 3 weitere Kugeln gleichen Durchmessers zwischen die 7 oberen und 7 unteren Kugeln passen. Diese 3 Kugeln berühren sich untereinander und stoßen in je eine Lücke innerhalb der 7 oberen und der 7 unteren Kugeln an diese an. Das Seitenverhältnis dieser hexagonalen Zelle (s. Bild 2) ist: $\textstyle {\frac {c}{a}}={\sqrt {\frac {8}{3}}}$ .

Die Stapelabfolge ihrer drei hexagonalen Kugelschichten wird ABA geschrieben.

Eine Elementarzelle mit hexagonal dichtester Packung (hdp) besteht aus zwei rautenförmigen Grundflächen. Die Atome befinden sich innerhalb der Elementarzelle auf den kristallographischen Lagen 1/3, 2/3, 1/4 und 2/3, 1/3, 3/4 (ein Symmetriezentrum der Struktur liegt dann konventionsgemäß in 0, 0, 0).[1]

Viele Metalle kristallisieren in einer hexagonal dichtesten Kugelpackung: Be, Mg, Sc, Ti, Co, Zn, Y, Zr, Tc, Ru, Cd, Lu, Hf, Re, Os, Tl und einige Lanthanoide. Als prominentester Vertreter gilt Magnesium, weshalb dieser Strukturtyp auch Magnesiumtyp genannt wird.

Literatur

Martin Okrusch, Siegfried Matthes: Mineralogie. 7. Auflage. Springer Verlag, Berlin 2005, ISBN 3-540-23812-3
Hans Murawski, Wilhelm Meyer: Geologisches Wörterbuch. 12. Auflage. Spektrum Akademischer Verlag, Heidelberg 2010, ISBN 978-3-8274-1810-4.
Rüdiger Borchert, Siegfried Turowski: Symmetrielehre der Kristallographie; Modelle der 32 Kristallklassen. Oldenbourg Wissenschaftsverlag GmbH, München, Wien 1999, ISBN 3-486-24648-8, S. 52–64.
Werner Massa: Kristallstrukturbestimmung. 3. Auflage. B. G. Teubner GmbH, Stuttgart/Leipzig/Wiesbaden 2002, ISBN 3-519-23527-7.
Ulrich Müller: Anorganische Strukturchemie. 4. Auflage. B. G. Teubner / GWV Fachverlage GmbH, Wiesbaden 2004, ISBN 3-519-33512-3, S. 182.
Hahn, Theo (Hrsg.): International Tables for Crystallography Vol. A D. Reidel publishing Company, Dordrecht 1983, ISBN 90-277-1445-2
Will Kleber, et al. Einführung in die Kristallographie 19. Auflage Oldenbourg Wissenschaftsverlag, München 2010, ISBN 978-3-486-59075-3
Walter Borchard-Ott Kristallographie 7. Auflage Springer Verlag, Berlin 2009, ISBN 978-3-540-78270-4

Einzelnachweise

Lothar Spieß, Robert Schwarzer, Gerd Teichert, Herfried Behnken: Moderne Röntgenbeugung: Röntgendiffraktometrie für Materialwissenschaftler, Physiker und Chemiker. Vieweg + Teubner, Wiesbaden 2009, ISBN 978-3-8351-0166-1, S. 57.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Hinweise-1] Bei den Angaben zu den physikalischen Eigenschaften bedeutet „−“ aufgrund der Symmetrie verboten und „+“ erlaubt. Über die Größenordnung der optischen Aktivität, Pyro- und Piezoelektrizität sowie des SHG-Effekts kann rein aufgrund der Symmetrie keine Aussage getroffen werden. Man kann aber davon ausgehen, dass stets eine zumindest schwache Ausprägung der Eigenschaft vorhanden ist. Für die Pyroelektrizität ist, sofern vorhanden, auch die Richtung des pyroelektrischen Vektors angegeben.

[2] Lothar Spieß, Robert Schwarzer, Gerd Teichert, Herfried Behnken: Moderne Röntgenbeugung: Röntgendiffraktometrie für Materialwissenschaftler, Physiker und Chemiker. Vieweg + Teubner, Wiesbaden 2009, ISBN 978-3-8351-0166-1, S. 57.