Packungsdichte (Kristallographie)

Die Packungsdichte (auch Packungsverhältnis oder Raumerfüllung genannt, englisch APF für atomic packing factor) ist in der Kristallographie definiert als das Verhältnis des Volumens der Atome, die sich in einer Elementarzelle befinden, zum Gesamtvolumen der Elementarzelle.

Der Begriff wurde analog in die Mathematik für räumliche Optimierungsprobleme übernommen, etwa Kugelpackungen, die in der Theorie der Datenkompression eine Rolle spielen.

Grundlagen

Die Atome werden dabei als harte, inkompressible Kugeln mit maximaler und identischer Größe angenommen. Der Zahlenwert der Packungsdichte ist charakteristisch für die Art der Packung. Sie hängt nicht von der Auffassung der Elementarzelle ab (Die Kugeln aus zwei oder mehr Elementarzellen erfüllen denselben Raumanteil wie in einer Elementarzelle). Aus der Raumerfüllung lassen sich weitere Schlüsse über die Gestalt des Gitters ziehen und beispielsweise die Stabilität oder die Dichte eines Kristalls begründen.

Allgemein ergibt sich die Packungsdichte $P$ aus:

P={\frac {N\cdot V_{\text{Atom}}}{V_{\text{Elementarzelle}}}}

wobei $N$ die Anzahl der Atome (= die Summe der einzelnen Anteile) in der Elementarzelle ist. Das Volumen der Kugeln in der Elementarzelle mit Radius berechnet sich durch:

V_{\text{Atom}}=V_{\text{Kugel}}(r)={\frac {4}{3}}\pi r^{3}

Bei vielen Kristallsystemen ist die Elementarzelle kubisch. Das Volumen einer solchen Elementarzelle mit dem Gitterparameter $a$ beträgt:

V_{\text{Elementarzelle}}=a^{3}

Für Packungen mit kubischer Elementarzelle gilt folglich:

P={\frac {N\cdot {\frac {4}{3}}\pi r^{3}}{a^{3}}}

Geht man von nur einer Atomsorte mit identischer Atomgröße aus, so ist die größtmögliche Raumerfüllung die einer kubisch dichtesten Kugelpackung (kubisch flächenzentrierte Gitter) und die hexagonal dichteste Kugelpackung. Sie beträgt ungefähr 74%.

Kristallstruktur von Elementen

In den hier aufgeführten Packungstypen kristallisieren die meisten Elemente aus.

Berechnung der Raumerfüllung

Kubisch Primitive Packung

Ausschnitt aus einer kubisch primitiven Packung. In Jeder Elementarzelle befindet sich zusammengerechnet 8*1/8 = 1 Kugel.

In einer kubisch primitiven Packung (englisch: scp, simple cubic packing) besetzen die Kugeln die 8 Ecken der kubischen Elementarzelle. Da die Alpha-Modifikation von Polonium in diesem Typ kristallisiert, wird er oft mit dem Trivialnamen α-Polonium-Typ bezeichnet.

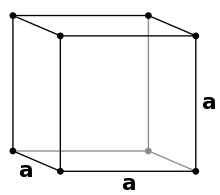
Die Kugeln der kubisch primitiven Elementarzelle sind hier vereinfacht als Punkte dargestellt

Von oben betrachtet sieht eine Schicht dieser Packung so aus:

Alle Schichten dieses Packungstyps sind also identisch. Mit ihrem Volumen füllt jede Kugel $1/8$ des Volumens in jeweils $8$ umliegenden Elementarzellen. Jede Elementarzelle ist insgesamt mit einem Kugelvolumen gefüllt. Jede Kugel berührt 6 andere Kugeln direkt, die Koordinationszahl ist 6. Alle Kugeln berühren sich lückenlos. Der Gitterparameter $a$ ist das zweifache des Kugelradius $r$ :

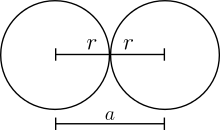
Somit ist

r={\frac {a}{2}}

Die Packungsdichte ist ungefähr 52,36%

P={\frac {N\cdot {\frac {4}{3}}\pi r^{3}}{a^{3}}}={\frac {1\cdot {\frac {4}{3}}\pi r^{3}}{a^{3}}}={\frac {{\frac {4}{3}}\pi ({\frac {a}{2}})^{3}}{a^{3}}}={\frac {\pi }{6}}\approx 0{,}5236

Kubisch flächenzentrierte Packung

In einer kubisch flächenzentrierten Packung (englisch: fcc, face centered cubic) besetzen 8 Kugeln die Ecken einer kubischen Elementarzelle und füllen sie mit 1/8 ihres Kugelvolumens. Zusätzlich befinden sich auf der Mitte der 6 Flächen eine Kugel, welche 1/2 ihres Volumens in die Elementarzelle hinzufüllt. Somit befinden sich in jeder Elementarzelle 8·1/8 + 6·1/2 = 4 Kugeln. Da Kupfer in diesem Typ kristallisiert, wird er auch als Kupfer-Typ bezeichnet.

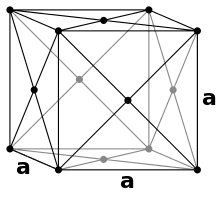
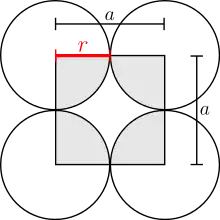
Die Elementarzelle einer kubisch flächenzentrierte Packung.

Ausschnitt der Elementarzelle einer kubisch flächenzentrierten Packung.

Die oberste und unterste Schicht sind gleich. Hier berühren sich die Kugeln entlang der Diagonalen der Elementarzelle:

Die mittlere Schicht sieht von oben betrachtet wie folgt aus:

Die Kugeln auf den Ecken berühren andere Kugeln auf Ecken folglich nicht. Der Radius aller Kugeln ist trotzdem gleich. Der Satz des Pythagoras folgert:

a^{2}+b^{2}=c^{2}

a=b\Rightarrow 2a^{2}=c^{2}

c={\sqrt {2}}a=4r

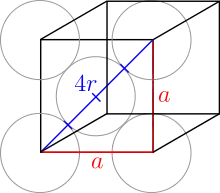
Der Radius ist also

r={\frac {{\sqrt {2}}a}{4}}

Die Packungsdichte beträgt ungefähr 74,05%

P={\frac {N\cdot {\frac {4}{3}}\pi r^{3}}{a^{3}}}={\frac {4\cdot {\frac {4}{3}}\pi r^{3}}{a^{3}}}={\frac {4\cdot {\frac {4}{3}}\pi ({\frac {{\sqrt {2}}a}{4}})^{3}}{a^{3}}}={\frac {{\sqrt {2}}\pi }{6}}\approx 0{,}7405

Kubisch raumzentrierte Packung

Ausschnitt der Elementarzelle einer kubisch raumzentrierten (innenzentrierten) Packung.

In einer kubisch innenzentrierten (auch: „raumzentrierten“) Packung (englisch: bcc, body centered cubic) sitzen wie ebenfalls 8 Kugeln auf den Ecken der kubischen Elementarzelle. Die Kugeln berühren sich an den Ecken nicht. In der Mitte der Elementarzelle sitzt eine Kugel, deren ganzes Volumen von der Elementarzelle eingeschlossen ist. Hier befinden sich also 8·1/8 + 1 = 2 Kugeln in der Elementarzelle. Dieser Typ wird mit dem Trivialnamen Wolfram-Typ bezeichnet.

Die oberste und unterste Schicht sehen wie folgt aus:

In der mittleren Schicht sitzt die volle Kugel:

Auch bei diesem Typ haben alle Kugeln denselben Radius. Die Kugeln berühren sich entlang der Raumdiagonalen durch die Elementarzelle.

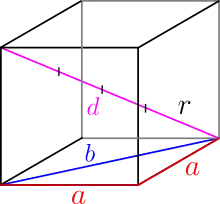
Um die Raumdiagonale zu berechnen benötigt man die Flächendiagonale. Es wird also zweimal der Satz des Pythagoras angewandt:

2a^{2}=b^{2}

b={\sqrt {2}}a

und

a^{2}+({\sqrt {2}}a)^{2}=d^{2}=3a^{2}

d={\sqrt {3}}a

Der Radius entspricht:

4r={\sqrt {3}}a

r={\frac {{\sqrt {3}}a}{4}}

Die Packungsdichte beträgt ungefähr 68%

P={\frac {N\cdot {\frac {4}{3}}\pi r^{3}}{a^{3}}}={\frac {2\cdot {\frac {4}{3}}\pi r^{3}}{a^{3}}}={\frac {2\cdot {\frac {4}{3}}\pi ({\frac {{\sqrt {3}}a}{4}})^{3}}{a^{3}}}={\frac {{\sqrt {3}}\pi }{8}}\approx 0{,}6802

Anwendungen

Mit der Kenntnis der Packung können beispielsweise Dichte, Molare Masse uvm. berechnet werden.

Beispiel

Die Dichte ist eine intensive Größe, die nicht von der Größe des betrachteten Systems abhängt. Die Dichte eines Kubikmeters eines Metalls ist identisch mit der Dichte der Elementarzelle der Struktur des Metalls. Unter Kenntnis des Gitterparameters, der Molaren Masse und der Anzahl der Atome pro Elementarzelle kann die Dichte z. B. eines Metalls wie folgt berechnet werden:

\rho ={\frac {m}{V}}

\Leftrightarrow \rho ={\frac {M\cdot n}{V}}={\frac {M\cdot N}{N_{A}\cdot V}}

Kupfer kristallisiert in einem kubisch-dicht gepackten Gitter. Es befinden sich also $4$ Atome in einer Elementarzelle. Der Radius eines Kupferatoms beträgt $1{,}28$ Å, das entspricht $1{,}28\cdot 10^{-10}\,\mathrm {m}$ .

\rho ={\frac {63{,}456\,\mathrm {\frac {g}{mol}} \cdot 4}{6{,}022140\cdot 10^{23}{\frac {1}{\mathrm {mol} }}\cdot a^{3}}}

Der Gitterparameter $a$ berechnet sich für diesen Typ wie folgt:

a={\frac {4r}{\sqrt {2}}}={\frac {4\cdot 1{,}28\cdot 10^{-10}\,\mathrm {m} }{\sqrt {2}}}=3{,}62\cdot 10^{-10}\,\mathrm {m}

Die Dichte von Kupfer ist:

\rho ={\frac {63{,}456\mathrm {\frac {g}{mol}} \cdot 4}{6{,}022140\cdot 10^{23}{\frac {1}{\mathrm {mol} }}\cdot (3{,}62\cdot 10^{-10}\,\mathrm {m} )^{3}}}=8897574{,}9\,\mathrm {\frac {g}{m^{3}}} =8{,}9\,\mathrm {\frac {g}{cm^{3}}}

Weblinks

Berechnungen der Packungsdichten, Fachinformationszentrum Chemie Berlin (ChemgaPedia)
Berechnung von Packungsdichten verschiedener kubischer Kristallstrukturen

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.