Keplersche Vermutung
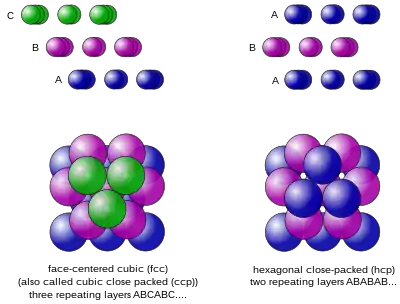
Die Keplersche Vermutung ist die von Johannes Kepler geäußerte Vermutung, dass bei der dichtesten Kugelpackung im dreidimensionalen euklidischen Raum keine Anordnung von gleich großen Kugeln eine größere mittlere Dichte aufweist als die kubisch-flächenzentrierte Packung und die hexagonale Packung. Beide Packungen haben die gleiche mittlere Dichte von etwas mehr als 74 Prozent.
1998 gab Thomas Hales bekannt, dass er einen Beweis für die Keplersche Vermutung gefunden habe. Der Computerbeweis überzeugte zunächst nicht alle Mathematiker. Durch den 2017 veröffentlichten formalen Beweis von Hales und Mitarbeitern gilt die Keplersche Vermutung als bewiesen.
Hintergrund
Man stelle sich ein großes Behältnis mit kleinen, gleich großen Kugeln vor. Die Dichte der Anordnung der Kugeln ist der Anteil vom Volumen des Behältnisses, der von den Kugeln eingenommen wird. Um die Anzahl der Kugeln im Behältnis zu maximieren, muss man die Anordnung mit der höchstmöglichen Dichte finden, sodass die Kugeln so dicht wie möglich gepackt werden.
Experimente zeigen, dass ein zufälliges Hineinschütten der Kugeln zu einer Dichte von ungefähr 65 Prozent führt. Eine höhere Dichte kann jedoch durch eine Anordnung der Kugeln in der folgenden Art und Weise erreicht werden: Begonnen wird mit einer Ebene Kugeln, die in einem hexagonalen Gitter angeordnet wird. Anschließend wird die nächste Ebene in die tiefsten Punkte der vorangehenden Ebene gelegt usw. Auf diese Weise werden z. B. Äpfel auf dem Markt gestapelt. Diese natürliche Art, die Kugeln zu stapeln, ergibt unendlich viele Möglichkeiten, von denen die kubisch-flächenzentrierte Packung und die hexagonale Packung die bekanntesten und am häufigsten in der Natur vorkommenden sind. Jede dieser Kugelpackungen hat eine mittlere Dichte von
Die Keplersche Vermutung besagt, dass diese Packungen bestmöglich sind – mit keiner Packung kann eine höhere Dichte erzeugt werden als mit diesen.
Geschichte

Ursprung
Die Vermutung ist benannt nach Johannes Kepler, der sie 1611 in Strena seu de nive sexangula (Über die sechseckige Schneeflocke) aufstellte. In dieser Schrift untersuchte Kepler die mathematischen Konstruktionsprinzipien von Schneeflocken, Bienenwabenzellen und Granatapfelkernen. Er suchte nach einer allgemeinen Theorie der Selbststrukturierung der Natur und formulierte nicht nur das Prinzip der dichtesten Packung, sondern auch das Prinzip der geringsten Wirkung.[1] Kepler begann aufgrund seines Briefwechsels mit dem englischen Mathematiker und Astronomen Thomas Harriot im Jahre 1606 die Anordnung von Kugeln zu untersuchen. Harriot war ein Freund und Assistent von Sir Walter Raleigh, der Harriot mit der Untersuchung des Problems beauftragte, wie die Kanonenkugeln am besten auf seinen Schiffen verstaut werden könnten. Harriot veröffentlichte 1591 eine Untersuchung von verschiedenen Anordnungen von Kugeln und entwickelte dabei auch eine frühe Version des Atommodells.
19. Jahrhundert
Kepler hatte keinen Beweis seiner Vermutung. Der erste Schritt zu einem Beweis wurde vom deutschen Mathematiker Carl Friedrich Gauß gemacht, der 1831 eine Teillösung veröffentlichte. Gauß bewies, dass die Keplersche Vermutung wahr ist, wenn die Kugeln in einem regelmäßigen Gitter angeordnet werden müssen.
Diese Aussage bedeutet, dass eine Anordnung von Kugeln, welche die Keplersche Vermutung widerlegen würde, eine unregelmäßige Anordnung sein müsste. Der Ausschluss aller möglichen unregelmäßigen Anordnungen ist jedoch sehr schwierig, wodurch der Beweis der Vermutung so schwierig wird. Es ist sogar bekannt, dass es unregelmäßige Anordnungen gibt, die in einem kleinen Bereich dichter als die kubische-flächenzentrierte Packung sind, aber jeder Versuch, diese Anordnungen auf ein größeres Volumen auszudehnen, verringert ihre Dichte.
Nach Gauß wurde im 19. Jahrhundert kein weiterer Fortschritt beim Beweis der Keplerschen Vermutung gemacht. 1900 nahm David Hilbert das Problem in seine Liste von 23 mathematischen Problemen auf – es ist ein Spezialfall von Hilberts 18. Problem.
20. Jahrhundert
Der nächste Schritt zu einer Lösung des Problems wurde von dem ungarischen Mathematiker László Fejes Tóth gemacht. 1953 bewies Fejes Tóth, dass das Problem der Berechnung des Maximums aller (regelmäßigen und unregelmäßigen) Anordnungen auf die Betrachtung einer endlichen (aber sehr großen) Anzahl von Fällen reduziert werden kann. Das bedeutete, dass ein Beweis durch eine sehr große Fallunterscheidung prinzipiell möglich war. Damit stellte Fejes Tóth als erster fest, dass mithilfe eines ausreichend schnellen Computers dieses theoretische Ergebnis in einen praktischen Ansatz zum Beweis der Vermutung umgesetzt werden kann.
In der Zwischenzeit wurden Versuche unternommen, eine obere Grenze für die maximale Dichte von allen möglichen Kugelanordnungen zu finden. Der englische Mathematiker Claude Ambrose Rogers bewies 1958 eine obere Grenze von ungefähr 78 Prozent, und nachfolgende Anstrengungen von anderen Mathematikern konnten diese Grenze leicht verringern, aber auch diese war immer noch ein ganzes Stück über der Dichte der kubisch-flächenzentrierten Packung von 74 Prozent.
Weiterhin gab es auch einige fehlgeschlagene Beweise. Der US-amerikanische Architekt Richard Buckminster Fuller behauptete 1975, einen Beweis gefunden zu haben, der sich jedoch sehr bald als unrichtig herausstellte. 1993 veröffentlichte der chinesisch-amerikanische Mathematiker Wu-Yi Hsiang an der Universität von Berkeley einen Aufsatz, in dem er behauptete, die Keplersche Vermutung mit geometrischen Mitteln zu beweisen. Einige Experten widersprachen dem, da er unzureichende Begründungen für einige seiner Behauptungen gebe. Obwohl nichts per se Falsches in Hsiangs Arbeit gefunden wurde (nachdem dieser die Preprints seines Beweises allerdings stetig nachbesserte), herrscht ein genereller Konsens, dass Hsiangs Beweis unvollständig ist. Einer der lautstärksten Kritiker war Thomas Hales, der zu dieser Zeit an seinem eigenen Beweis arbeitete.
Hales’ Beweis
1998 gab Thomas Hales, zurzeit Andrew-Mellon-Professor an der Universität Pittsburgh, bekannt, dass er einen Beweis für die Keplersche Vermutung gefunden habe. Hales’ Beweis ist ein Beweis durch Fallunterscheidung, bei dem er viele unterschiedliche Fälle mittels komplexer Berechnungen am Computer untersucht.
Dem Ansatz von Fejes Tóth folgend ermittelte Thomas Hales, zu dieser Zeit an der Universität von Michigan, dass die maximale Dichte aller Kugelanordnungen durch die Minimierung einer Funktion mit 150 Variablen gefunden werden kann. 1992 begann er, unterstützt durch seinen Doktoranden Samuel P. Ferguson, ein Forschungsprogramm, das Methoden der linearen Optimierung anwendet, um eine untere Grenze für diese Funktion, angewendet auf eine Menge von über 5.000 Kugelanordnungen, zu bestimmen. Falls für jede dieser Kugelanordnungen eine untere Grenze für den Funktionswert gefunden würde, die größer ist als der Funktionswert für die kubisch-flächenzentrierte Packung, dann wäre die Keplersche Vermutung bewiesen. Um die unteren Grenzen für alle Fälle zu bestimmen, mussten mehr als 100.000 einzelne lineare Optimierungen berechnet werden.
Als Hales 1996 den Fortschritt seiner Arbeit präsentierte, sagte er, das Ende sei in Sicht, aber es könne noch „ein Jahr oder zwei“ dauern. Im August 1998 kündigte Hales an, dass der Beweis vollständig sei. Zu diesem Zeitpunkt bestand er aus 250 Seiten Aufzeichnungen und drei Gigabyte Computerprogrammen, Daten und Ergebnissen.
Trotz der ungewöhnlichen Form des Beweises schlug Robert MacPherson, einer der Herausgeber der renommierten mathematischen Zeitschrift Annals of Mathematics, eine Veröffentlichung in dieser Zeitschrift vor. Die Begutachtung des Computerbeweises musste jedoch höchsten Ansprüchen genügen, sodass der Beweis zunächst einem Gremium aus zwölf Gutachtern vorgelegt wurde. Gábor Fejes Tóth, der Sprecher der Gutachter (und der Sohn von László Fejes Tóth), gab 2003 nach vier Jahren Arbeit bekannt, dass sich die Gutachter zu „99 Prozent sicher“ seien, dass der Beweis korrekt sei, aber sie könnten nicht die Korrektheit aller am Computer durchgeführten Berechnungen zertifizieren. MacPherson merkte daraufhin an, dass die Gutachter es möglicherweise leichter gehabt hätten und auch zu einer eindeutigen Antwort gekommen wären, wenn Hales’ Manuskript lesbarer und verständlicher gewesen wäre. Als Resultat des Gutachtens wird angenommen, dass die Keplersche Vermutung nunmehr ein mathematischer Satz werden könnte.
Im Mai 2003 veröffentlichte Hales einen hundertseitigen Aufsatz als Preprint, der den nicht vom Computer berechneten Teil seines Beweises im Detail beschreibt.[2] Die Annals of Mathematics veröffentlichten 2005 den theoretischen Teil von Hales’ Beweis, der von dem Gutachtergremium erfolgreich überprüft wurde.[3] Die Ergebnisse der Computerberechnungen – das heißt eine vollständigere Veröffentlichung in Form der Überarbeitung der Preprints von 1998 – wurden in einer dafür spezialisierten Zeitschrift, Discrete and Computational Geometry, veröffentlicht.[4]
Formaler Beweis
Im Januar 2003 kündigte Hales den Start eines gemeinschaftlichen Projektes an, das einen vollständig formalen Beweis von Keplers Vermutung erstellen soll. Das Ziel dieses Projektes war, jeden verbliebenen Zweifel an der Gültigkeit des Beweises auszuräumen, indem computergestützt ein formaler Beweis in Objective CAML erstellt wird, der von interaktiven Theorembeweisern wie z. B. John Harrisons HOL light überprüft werden kann. Das Projekt heißt Project FlysPecK, wobei das F, P und K für Formal Proof of Kepler stehen. Hales schätzte, dass die Erstellung des formalen Beweises etwa 20 Jahre dauern werde. Im August 2014 verkündete er, dass eine Übertragung des Beweises in computerisierte Form gelungen sei und die Software die Richtigkeit des Beweises bestätigt habe.[5]
Im Januar 2015 veröffentlichten Hales und 21 Co-Autoren ein Paper mit dem Titel A formal proof of the Kepler conjecture auf dem Preprintserver arXiv, und beanspruchten die Vermutung bewiesen zu haben. 2017 wurde der Beweis im Journal Forum of Mathematics, Pi veröffentlicht.[6]
Literatur
- George Szpiro: Kepler's conjecture. Wiley, Hoboken, 2003. ISBN 0-471-08601-0
- George G. Szpiro: Die Keplersche Vermutung. Springer Berlin, 2011. ISBN 978-3-642-12740-3
- Thomas C. Hales: An Overview of the Kepler Conjecture, 1998, Preprint
- Thomas C. Hales: A proof of the Kepler Conjecture, Annals of Mathematics. Band 162, 2005, S. 1063–1183 (Sektion 5 ist mit Ferguson verfasst Übersicht über den Beweis)
- Thomas Hales, Samuel Ferguson (Herausgeber Gábor Fejes Tóth, Jeffrey Lagarias): Sonderheft von Discrete & Computational Geometry, Band 36, 2006, Nr. 1 zum Beweis der Kepler-Vermutung. Darin:
- Hales: Historical Overview of the Kepler Conjecture, S. 5–20, Hales, Ferguson A Formulation of the Kepler Conjecture, S. 21–69, Hales Sphere Packing, III. Extremal Cases, S. 71–110, Hales Sphere Packing, IV. Detailed Bounds, S. 111–166, Ferguson Sphere Packings, V. Pentahedral Prisms, S. 167–204, Hales Sphere Packings, VI. Tame Graphs and Linear Programs, S. 205–265
- Thomas C. Hales, John Harrison, Sean McLaughlin, Tobias Nipkow, Steven Obua, Roland Zumkeller: A Revision of the Proof of the Kepler Conjecture. Discrete & Computational Geometry, Band 44, 2010, S. 1–34
- Jeffrey Lagarias: Bounds for local density of sphere packings and the Kepler conjecture, Discrete & Computational Geometry, Band 27, 2002, 165–193
- Jeffrey Lagarias (Herausgeber), Thomas Hales, Samuel Ferguson: The Kepler Conjecture. The Hales-Ferguson Proof, Springer Verlag 2011 (Abdruck der Originalarbeiten von Hales, Ferguson mit Einleitung von Lagarias und dem Übersichtsartikel von Lagarias von 2002)
- Joseph Oesterlé: Densité maximale des empilements de sphères en dimension 3, d'après Thomas C. Hales et Samuel P. Ferguson, Seminaire Bourbaki Nr. 863, 1999
Weblinks
- Artikel auf www.mathematik.de
- www.zeit.de – zur Problematik eines Beweises mit Computer
- Thomas Hales: A proof of the Kepler conjecture, Annals of Mathematics, 162 (2005), 1065–1185 (engl.)
- Überblick über Hales’ Beweis (engl.)
- Dana Mackenzies Artikel im American Scientist (engl.), Archivlink abgerufen am 1. März 2022
- Die Keplersche Vermutung – populärwissenschaftliche Weihnachtsvorlesung (in zwei Teilen) von Edmund Weitz auf YouTube
Einzelnachweise
- Marie-Luise Heuser, Keplers Theorie der Selbststrukturierung von Schneeflocken vor dem Hintergrund neuplatonischer Philosophie der Mathematik, in: Selbstorganisation. Jahrbuch für Komplexität in den Natur-, Sozial- und Geisteswissenschaften, hrsg. v. Uwe Niedersen, Bd. 3: Konzepte von Chaos und Selbstorganisation in der Geschichte der Wissenschaften, Berlin (Duncker & Humblot) 1992, S. 237–258.
- Thomas C. Hales: A computer verification of the Kepler conjecture. In: arXiv:math/0305012. 30. April 2003, arxiv:math/0305012.
- A proof of the Kepler conjecture | Annals of Mathematics. Abgerufen am 18. März 2019 (amerikanisches Englisch).
- Thomas C. Hales, Samuel P. Ferguson: A Formulation of the Kepler Conjecture. In: Discrete & Computational Geometry. Band 36, Nr. 1, Juli 2006, ISSN 0179-5376, S. 21–69, doi:10.1007/s00454-005-1211-1 (springer.com [abgerufen am 18. März 2019] Weitere Aufsätze von Hales, Ferguson in demselben Heft).
- derStandard.at – Beweis für 400 Jahre altes Stapelproblem bestätigt. Artikel vom 15. August 2014, abgerufen am 16. August 2014.
- Thomas Hales, Mark Adams, Gertrud Bauer, Tat Dat Dang, John Harrison: A formal proof of the Kepler conjecture. In: Forum of Mathematics, Pi. Band 5, 2017, ISSN 2050-5086, doi:10.1017/fmp.2017.1 (cambridge.org [abgerufen am 18. März 2019]).