Tests der speziellen Relativitätstheorie
Tests der speziellen Relativitätstheorie werden bis heute durchgeführt. Sie waren für die Entwicklung und Akzeptanz der Theorie von entscheidender Bedeutung; moderne Experimente ergeben weiterhin Übereinstimmung mit der Theorie. Entgegen populären Darstellungen ist die spezielle Relativitätstheorie nicht bloß das Ergebnis von Gedankenexperimenten und wurde nicht nur zur Erklärung eines einzelnen Versuchsergebnisses, des berühmten Michelson-Morley-Experiments, entwickelt. Die Stärke der Theorie liegt vielmehr darin, dass sie die einzige ist, die mehrere grundverschiedene Experimente widerspruchsfrei erklären kann. Neben den klassischen Experimenten gibt es heute Tests der Theorie auch z. B. im experimentell schwer zugänglichen Bereich der Planck-Skala oder in der Neutrino-Physik. Bislang bestätigen auch deren Resultate die Vorhersagen der Theorie. Zusammenstellungen diverser Tests wurden von Jakob Laub,[1] Zhang,[2] Mattingly,[3] Clifford Will,[4] und Roberts/Schleif[5] gegeben.
Der Gültigkeitsbereich der speziellen Relativitätstheorie ist eingeschränkt auf alle Phänomene in der „flachen Raumzeit“, d. h. alle gleichförmigen und beschleunigten Bewegungen bei Abwesenheit der Gravitation. Letzteres behandelt die allgemeine Relativitätstheorie; für die entsprechenden experimentellen Tests siehe Tests der allgemeinen Relativitätstheorie.
Experimente, die den Weg zur SRT ebneten
Die im 19. Jahrhundert vorherrschende Theorie war diejenige des ruhenden Äthers, eines Mediums, in dem sich Licht ausbreitet, wie sich etwa der Schall in Luft ausbreitet. Daraus folgt, dass sich Licht in diesem Äther konstant und unabhängig von der Geschwindigkeit der Lichtquelle ausbreitet. Ein Beobachter, der sich relativ zu diesem Äther bewegt, müsste folglich eine Art „Ätherwind“ messen können, genauso wie ein relativ zur Luft bewegter Beobachter einen Fahrtwind bemerken muss.
Experimente erster Ordnung
Es wurden nun eine Reihe optischer Experimente durchgeführt, die trotz ihrer relativen Ungenauigkeit eigentlich ein positives Resultat hätten erbringen müssen, wenn der Äther vollständig in Ruhe wäre. Doch konnte dieses Problem von Augustin Jean Fresnel (1818) durch Einführung einer Hilfshypothese gelöst werden. Er führte den sogenannten fresnelschen Mitführungskoeffizienten ein, der besagt, dass ein Bruchteil des Äthers abhängig vom Brechungsindex der Materie mitgeführt wird. Die Notwendigkeit dieses Mitführungskoeffizienten in der Äthertheorie wurde direkt durch das Fizeau-Experiment (1851) nachgewiesen. Später konnte gezeigt werden, dass alle optischen Ätherdriftexperimente erster Ordnung aus diesem Grund ein negatives Resultat erbringen müssen. Daneben wurden auch elektrostatische Experimente durchgeführt. Deren negatives Ergebnis konnte mit der Theorie von Fresnel nicht erklärt werden, und so musste Hendrik Antoon Lorentz (1892, 1895) eine Reihe von Hilfsvariablen für bewegte Beobachter einführen. Dazu gehört eine Ortsvariable, gemäß der sich elektrostatische Felder in Bewegungsrichtung kontrahieren, und eine Zeitvariable, gemäß der die Zeitkoordinaten vom jeweiligen Ort abhängen, die sogenannte „Ortszeit“. Dadurch war sichergestellt, dass alle optischen und elektrostatischen Experimente erster Ordnung ein negatives Resultat erbringen mussten.[1]
Experimente zweiter Ordnung

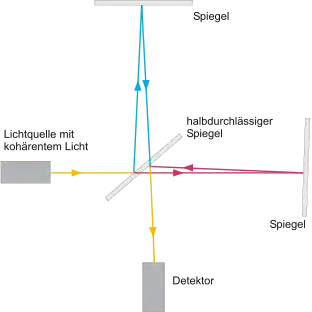
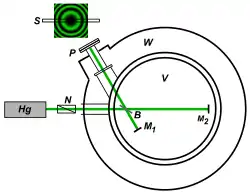
Die Fresnel-Lorentzsche Theorie des ruhenden Äthers musste allerdings positive Resultate erbringen, wenn die Experimente genau genug waren, um Größen zweiter Ordnung in v/c messen zu können. Das erste Experiment dieser Art war das Michelson-Morley-Experiment (1881, 1887), mit dem mittels eines Interferometers, mit Hilfe dessen zwei Strahlen senkrecht zueinander gespiegelt und wieder zusammengeführt wurden, die Veränderung der Strecke bzw. der relativen Lichtgeschwindigkeiten im Ätherwind gemessen werden sollte. Das Ergebnis war jedoch negativ. Der einzige Ausweg, um dieses Ergebnis mit einem ruhenden Äther verträglich zu machen, war die von George Francis FitzGerald (1889) und Lorentz (1892) aufgestellte Kontraktionshypothese. Diese besagt, dass (wie vorher schon bekannt war) nicht nur elektrostatische Felder kontrahieren, sondern auch die Bindungskräfte in der Materie davon betroffen sind, und somit die Materie selbst dieser Kontraktion unterworfen ist. Dies wurde plausibel gemacht durch die Annahme, dass die Bindungskräfte selbst elektrischer Natur sind. Da jedoch kein zwingender theoretischer Grund für diese Annahme gebracht werden konnte, wurde die Längenkontraktion als Ad-hoc-Hypothese angesehen.
Neben dem optischen Michelson-Morley-Experiment wurde 1903 auch dessen elektrodynamisches Äquivalent durchgeführt – das Trouton-Noble-Experiment. Hier sollte gezeigt werden, dass ein im Äther bewegter Kondensator ein Drehmoment aufweist. Doch auch hier war das Ergebnis negativ. Auch die Längenkontraktion wurde durch die Experimente von Rayleigh und Brace (1902, 1904) einer direkten Prüfung unterworfen, denn es wurde angenommen, dass diese zur Doppelbrechung führt – abermals war das Ergebnis negativ. (Das später durchgeführte Trouton-Rankine-Experiment (1908), welches nachweisen sollte, ob die Längenkontraktion einen Einfluss auf den Widerstand einer Spule hat, verlief ebenfalls negativ.)
Um nun alle vor 1904 durchgeführten Experimente zu erklären, musste Lorentz seine Theorie abermals erweitern, und führte deswegen im Rahmen der Lorentzschen Äthertheorie die vollständige Lorentz-Transformation ein, und Henri Poincaré erklärte (1905), dass die Nichtexistenz einer absoluten Bewegung (Relativitätsprinzip) offenbar ein Naturgesetz ist.
Widerlegungen des bewegten Äthers
Die Idee, dass der Äther vollständig innerhalb bzw. in der Nähe der Erde mitgeführt wird, wodurch die negativen Ätherdriftexperimente erklärt werden könnten, wurde widerlegt durch
- das Fizeau-Experiment,
- die Experimente von Oliver Lodge (1893), der anhand von rotierenden Scheiben herausfinden wollte, ob der Äther mitgeführt wird,
- das Hammar-Experiment (1935), bei dem ein Interferometerarm mit Blei umhüllt wurde und der andere freilag,
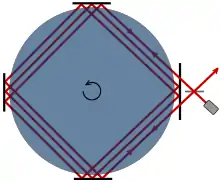
- den Sagnac-Effekt und
- durch die Existenz der Aberration des Lichtes.
Auch die Annahme, dass die Mitführung proportional der Masse sei und somit nur für die Erde als Ganzes zutrifft, wurde durch das Michelson-Gale-Experiment (Messung des Sagnac-Effekts durch die Erdrotation) widerlegt.
Spezielle Relativitätstheorie
Ausgangssituation
Albert Einstein zeigte 1905, dass folgende Modelle und Experimente
- die Maxwell-Lorentzsche Elektrodynamik (Unabhängigkeit der Lichtgeschwindigkeit von der Quellengeschwindigkeit)
- die elektromagnetische Induktion ist nur von der Relativbewegung abhängig
- die negativen Ätherdriftexperimente (kein bevorzugtes Bezugssystem)
- die Aberration des Lichtes und das Fizeau-Experiment (keine vollständige Äthermitführung)
nur dann ein logisch stimmiges Ganzes ergeben, wenn die Konstanz der Lichtgeschwindigkeit in allen Inertialsystemen und das Relativitätsprinzip angenommen wird. Das Ergebnis ist die spezielle Relativitätstheorie, in der die Konzepte von Raum und Zeit einer grundlegenden Revision unterworfen werden und die Galilei-Transformation durch die Lorentz-Transformation ersetzt wird. Die Lorentz-Transformation ist nun keine Ansammlung von Hilfsvariablen (wie noch bei Lorentz) mehr, sondern betrifft das Wesen von Raum und Zeit und spiegelt eine grundlegende (Lorentz-)Symmetrie wider, wobei sie zusätzlich die Grundlage für erfolgreiche Theorien wie das Standardmodell ist. Für den materiellen Äther als ein mit einem Bewegungszustand ausgestattetes, bevorzugtes Bezugssystem war von nun an kein Platz mehr. Mit dieser Lorentz-Symmetrie bzw. -Invarianz sind eine Reihe experimentell überprüfbarer Voraussagen verbunden:[6]
| Relativitätsprinzip | Konstanz der Lichtgeschwindigkeit | Zeitdilatation |
|---|---|---|
| Jeder gleichförmig bewegte Bewegter (der also in einem Inertialsystem ruht) ist mit Hilfe einer mitbewegten Experimentalanordnung nicht in der Lage, seinen „absoluten“ Bewegungszustand zu messen. | In allen Inertialsystemen ist die gemessene Lichtgeschwindigkeit unabhängig von der Geschwindigkeit der Lichtquelle in allen Richtungen gleich (Isotropie) und kann auch von massebehafteten Körpern nicht überschritten werden. | Eine Uhr C (also jeder periodische Prozess), welche zwischen zwei in einem Inertialsystem ruhenden und synchronisierten Uhren A und B hin- und herbewegt wird, geht gegenüber den Uhren A und B nach. |
| Daneben existieren noch weitere relativistische Effekte wie Längenkontraktion, Dopplereffekt, Aberration etc. Ebenso sind damit die experimentellen Vorhersagen relativistischer Theorien wie des Standardmodells verbunden. | ||
Grundlegende Experimente
Alle Aussagen der SRT können phänomenologisch aus folgenden drei Experimenten abgeleitet werden:[7]
- Michelson-Morley-Experiment, mit dem die Richtungsabhängigkeit der Lichtgeschwindigkeit bezüglich eines bevorzugten Bezugssystems getestet wird. Dadurch wird das Verhältnis zwischen longitudinalen und transversalen Längen bewegter Körper bestimmt.
- Kennedy-Thorndike-Experiment, mit dem die Abhängigkeit der Lichtgeschwindigkeit von der Relativgeschwindigkeit des Messapparats bezüglich eines bevorzugten Bezugssystems getestet wird. Dadurch wird das Verhältnis zwischen longitudinaler Länge und der Dauer der Zeitabläufe bewegter Körper bestimmt.
- Ives-Stilwell-Experiment, mit dem der relativistische Dopplereffekt und damit die Zeitdilatation nachgewiesen wird.
Aus diesen Experimenten und unter Voraussetzung der Poincaré-Einstein-Synchronisation folgt die komplette Lorentz-Transformation, wobei der Lorentz-Faktor ist:[7]
- .
Die Kombination dieser Experimente ist nicht nur wichtig für die phänomenologische Herleitung der Lorentz-Transformation, sondern auch, weil für sich alleine genommen die meisten Experimente mehrdeutig interpretierbar sind. Beispielsweise können Isotropieexperimente wie das Michelson-Morley-Experiment auch als einfache Konsequenz des Relativitätsprinzips angesehen werden, wonach jeder Beobachter sich als ruhend ansehen kann. Damit sind diese Experimente auch mit Galilei-invarianten Theorien wie der Emissionstheorie oder der vollständigen Äthermitführung verträglich, in denen die Lichtgeschwindigkeit nicht konstant ist. Erst durch die Hinzunahme anderer Experimente, welche die konkurrierenden Galilei-invarianten Theorien ausschließen (wie das Ives-Stilwell-Experiment oder die Widerlegungen der Äthermitführung oder der Emissionstheorie) verbleibt lediglich die Lorentzinvarianz und somit die SRT als einzige Theorie, welche alle Experimente erklären kann.
Interferometrie, Resonatoren
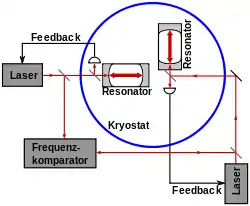
Zur Messung der Isotropie der Lichtgeschwindigkeit werden Varianten des Michelson-Morley-Experiments und des Kennedy-Thorndike-Experiments durchgeführt. Im Unterschied zu Michelson-Morley werden bei Kennedy-Thorndike-Experimenten unterschiedlich lange Arme benutzt, wobei die Auswertung über Monate erfolgt. Dadurch könnten etwaige Auswirkungen der Geschwindigkeitsänderungen des Apparats während der Rotation um die Sonne festgestellt werden. In modernen Resonator-Experimenten wurde unter Benutzung von optischen Resonatoren eine mögliche Anisotropie der Lichtgeschwindigkeit auf ∼10−17 verringert. Dabei werden nicht nur terrestrische Tests durchgeführt, sondern auch bei Benutzung von Lunar Laser Ranging, d. h. bei optischen Messungen zwischen Erde und Mond, konnte eine Variante des Kennedy-Thorndike-Experiments durchgeführt werden.
In den 1960ern wurden diverse Spielarten der Mößbauer-Rotor-Experimente durchgeführt, wo Sender und Empfänger auf einer rotierenden Scheibe angebracht wurden. Durch Ausnutzung des Mößbauer-Effekts konnte anhand der gemessenen Dopplerverschiebung eine Anisotropie der Lichtgeschwindigkeit mit großer Genauigkeit ausgeschlossen werden. (Ähnliche Experimente wurden auch zur Messung der Zeitdilatation verwendet, s. unten.)
Abhängigkeit von Quellengeschwindigkeit und Energie
Mit einer Emissionstheorie, die besagt, dass die Lichtgeschwindigkeit abhängig von der Geschwindigkeit der Lichtquelle ist, könnte der negative Ausgang der Ätherdriftexperimente ebenfalls erklärt werden. Eine Reihe von Tests hat jedoch gezeigt, dass die Lichtgeschwindigkeit unabhängig von der Quellgeschwindigkeit ist: beispielsweise Mesonenbeobachtungen, wo die Photonen nicht die Geschwindigkeit der zerfallenden Mesonen übernahmen, der Sagnac-Effekt und die Beobachtung von Doppelsternen, deren Umlaufbahnen bei unterschiedlich schneller Ausbreitung des Lichtes verzerrt erscheinen müssten.
Durch Beobachtung von Lichtstrahlen unterschiedlicher Energie (bis zu 31 GeV) von entfernten astronomischen Quellen konnte auch gezeigt werden, dass die Lichtgeschwindigkeit nicht von der Frequenz und Energie des Lichtes abhängt.[8]
Einweg-Messungen
Zusätzlich wurden eine Reihe von präzisen Einweg-Messungen mit Licht[5] durchgeführt, die allesamt die Vorhersagen der speziellen Relativitätstheorie bzw. die Isotropie der Lichtgeschwindigkeit bestätigten. Hier ist allerdings zu beachten, dass immer nur die Zweiweg-Lichtgeschwindigkeit, d. h. von A nach B wieder zurück nach A, direkt gemessen werden kann, denn die Einweg-Lichtgeschwindigkeit (von A nach B) hängt von der Definition der Gleichzeitigkeit und somit von dem gewählten Synchronisationsschema ab. Die Poincaré-Einstein-Synchronisation macht die Einweg- gleich der Zweiweg-Lichtgeschwindigkeit. Nun sind auch andere Synchronisationen und Theorien denkbar, die eine anisotrope Einweg-Lichtgeschwindigkeit ergeben und trotzdem experimentell mit der speziellen Relativitätstheorie äquivalent sind, da auch hier Phänomene wie Zeitdilatation bewegter Uhren auftreten und die Zweiweg-Lichtgeschwindigkeit konstant ist. Jedoch kann innerhalb dieser Klasse von Theorien nur die spezielle Relativitätstheorie ernsthaft in Betracht gezogen werden, da in ihr die Lorentz-Symmetrie klar zum Ausdruck kommt, während alle anderen Theorien (wie die lorentzsche Äthertheorie) nur durch eine Reihe von Hilfshypothesen und extremen Annahmen zur Uhrensynchronisation dieselben Ergebnisse erzielen können.
Isotropie von Raum, Masse und Energie
Ebenso wurden Messungen einer möglichen Anisotropie von Raum, Masse, Energie und damit zusammenhängend einer Verletzung der Lorentzinvarianz durch das Hughes-Drever-Experiment und diverser Spielarten davon vorgenommen. Im Gegensatz zu den Resonatorexperimenten an Photonen, werden hier die Eigenschaften von Protonen, Neutronen und Elektronen untersucht. Wenn beispielsweise die Lichtgeschwindigkeit nicht mit der Grenzgeschwindigkeit der Materie bzw. der atomaren Wechselwirkungen übereinstimmt, dann sollte dies zu Abweichungen in den Energieniveaus von Atomkernen führen. Die erreichte Genauigkeit, mit der eine Anisotropie ausgeschlossen werden kann, liegt aktuell bei ca. ∼10−24 eV, wodurch diese Experimente zu den genauesten Tests der SRT überhaupt zählen. Diese Experimente können auch als „Uhrenanisotropie-Experimente“ aufgefasst werden, da die verglichenen Frequenzen und periodischen Vorgänge als Uhren fungieren.[4][3]
Zeitdilatation und Längenkontraktion

Die Zeitdilatation und damit zusammenhängend der transversale relativistische Dopplereffekt konnte erstmals direkt durch das Ives-Stilwell-Experiment (1938) nachgewiesen werden, wo die Verschiebung des Schwerpunkts zwischen sich überlagernden Lichtwellen ausgewertet wurde. Moderne Ives-Stillwell-Messungen werden in Schwerionenspeicherringen mit Sättigungsspektroskopie durchgeführt, wobei eine maximale Abweichung von der Zeitdilatation von ∼10−8 erreicht worden ist. Eine andere Variante sind die Mößbauer-Rotor-Experimente, wo auf einer Scheibe Licht von einer Quelle in der Mitte zu einem Empfänger am Rand geschickt wird. Dabei wird der Dopplereffekt unter Ausnutzung des Mößbauer-Effekts durchgeführt.
Auch die Zeitdilatation bewegter Teilchen konnte durch Vergleich von Messungen in der Atmosphäre mit Teilchenbeschleuniger-Experimenten mit großer Genauigkeit bestätigt werden. Das Hafele-Keating-Experiment überprüft hingegen direkt das sogenannte Zwillingsparadoxon. In diesem Experiment spielt allerdings die gravitative Zeitdilatation der allgemeinen Relativitätstheorie eine wesentliche Rolle.
Während die Bestätigung der Zeitdilatation in Teilchenbeschleunigern bereits Routine ist, ist es praktisch kaum möglich, die Lorentzkontraktion direkt zu beobachten, da die Dimensionen der zu beobachtenden Teilchen zu klein sind. Jedoch gibt es indirekte Bestätigungen, wie das Verhalten bei Kollisionen von Schwerionen, welche nur erklärt werden können, wenn die erhöhte Dichte aufgrund der Lorentzkontraktion berücksichtigt wird. Ebenso führt die Kontraktion zu einer Verstärkung des Coulomb-Feldes senkrecht zur Bewegungsrichtung, deren Auswirkungen ebenfalls bereits beobachtet wurden. Dies alles führt dazu, dass relativistische Effekte wie Zeitdilatation und Längenkontraktion bei der Konstruktion von Teilchenbeschleunigern berücksichtigt werden müssen.
Relativistische Energie und Impuls
Seit 1901 wurden eine Reihe von Messungen durchgeführt, die überprüfen sollten, ob die Masse der Teilchen in Kathodenstrahlen abhängig ist von deren Geschwindigkeit. Die Ergebnisse zeigten tatsächlich eine solche Abhängigkeit, jedoch war die Genauigkeit, und damit die Brauchbarkeit bei der Unterscheidung verschiedener Konkurrenztheorien, lange umstritten. Schließlich konnte bei weiteren Experimenten eindeutig festgestellt werden, dass die Ergebnisse mit den Voraussagen der speziellen Relativitätstheorie übereinstimmen.
Heute werden diese Voraussagen betreffend der Zunahme der relativistischen Energie bereits routinemäßig in Teilchenbeschleunigern bestätigt, wie beispielsweise im Large Electron-Positron Collider (Elektron-Positron-Kollisionen) oder im Relativistic Heavy Ion Collider (Hadron-Kollisionen). Die relativistischen Formeln werden dabei nicht nur aufs genaueste bestätigt, sondern sind auch für die Konstruktion von Zyklotronen und Synchrotronen notwendig, durch welche die Partikel annähernd auf Lichtgeschwindigkeit beschleunigt werden.
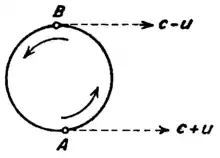
Sagnac und Fizeau
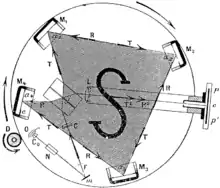
Eine weitere experimentelle Vorhersage der SRT besagt, dass zwei Strahlen, die in entgegengesetzte Richtungen einen geschlossenen Pfad durchlaufen, wobei Sender/Empfänger sich relativ zu diesem Pfad bewegen, unterschiedliche Zeitspannen benötigen, um zum Empfänger zurückzukehren (eine Folge der Unabhängigkeit der Lichtgeschwindigkeit von der Quelle, siehe oben). Dieser Effekt konnte tatsächlich mit Hilfe eines Sagnac-Interferometers nachgewiesen werden und muss heute beispielsweise auch für die Funktion des Navigationssystems GPS berücksichtigt werden.
Finden solche Versuche innerhalb dichter und bewegter Medien statt, muss dabei auch der durch das Fizeau-Experiment nachgewiesene fresnelsche Mitführungskoeffizient berücksichtigt werden. Dieser wurde oben zwar als Bestätigung eines annähernd ruhenden Äthers bezeichnet, jedoch ergibt sich dieser in der SRT als simple Konsequenz des relativistischen Geschwindigkeitsadditionstheorems für geringe Geschwindigkeiten.
Weitere moderne Tests
Der technische Fortschritt ermöglichte in den letzten Jahren eine Reihe von Hochpräzisionsmessungen zur Prüfung moderner Theorien der Quantengravitation, die möglicherweise minimale Verletzungen der Lorentzinvarianz zulassen. Dazu zählen auch Abweichungen vom schwachen Äquivalenzprinzip, da gemäß der allgemeinen Relativitätstheorie in frei fallenden Bezugssystemen eine „lokale Lorentzinvarianz“ (LLI) gilt.[3]
- Neben den oben bereits erwähnten modernen Variationen von Michelson-Morley und Kennedy-Thorndike, werden auch Uhrenanisotropie-Experimente im Sinne des Hughes-Drever-Experiments weiterhin ausgeführt, die den Protonen- und Neutronen-Sektor abdecken. Für mögliche Abweichungen von der Lorentzinvarianz im Elektronen-Sektor werden spinpolarisierte Torsionswaagen untersucht.
- Die Zeitdilatation wird in modernen Experimenten durch Beobachtung des Dopplereffekts von Lithium nachgewiesen, wobei diese Experimente für den Elektronen-, Protonen- und Photonen-Sektor gültig sind.
- Andere Experimente benutzen Penning-Fallen, wo in elektrostatischen- und Magnetfeldern Abweichungen von der Zyklotronbewegung im Magnetfeld und der Larmorpräzession beobachtet werden können.
- Abweichungen von der CPT-Symmetrie, deren Bruch in den meisten Fällen eine Verletzung der Lorentzinvarianz implizieren würde, werden durch Experimente an neutralen Mesonen, Penning-Fallen und Myonen bestimmt. Bislang wurden keine CPT-Verletzungen festgestellt.
- Andere Testmöglichkeiten sind Schwellenenergieeffekte bei Licht, Elektronen und anderen Teilchen. Eine Lorentz-Verletzung könnte dazu führen, dass die daraus folgenden Reaktionen nicht mehr den Standardwerten entsprechen.
- Geforscht wird nach räumlichen Anisotropien in den Neutrinooszillationen. Ebenso werden Messungen der Neutrinogeschwindigkeit durchgeführt.
- Astronomische Tests werden im Zusammenhang mit der Flugzeit von Photonen durchgeführt, wo mögliche, zur Lorentz-Verletzung führende Einflüsse von Dispersion und Doppelbrechung gemessen werden können. Dies könnte dazu führen, dass sich Photonen von unterschiedlicher Energie, Frequenz oder Polarisation unterschiedlich schnell ausbreiten. Als weitere Kandidaten zu Untersuchungen bieten sich vor allem Synchrotronstrahlen an. Ebenso werden Beugungsringe nach möglichen Abweichungen von der Lorentzinvarianz untersucht, deren Photonen dadurch außer Phase geraten können.
- Zusätzlich werden Beobachtungen im Higgs-Sektor angestellt.
Testtheorien
Aufgrund der mannigfaltigen Möglichkeiten einer Verletzung der Lorentzinvarianz aufgrund von Quantenphänomenen in modernen Experimenten wurden verschiedene Testtheorien entwickelt, welche durch Beifügung verschiedener Parameter in ihren experimentellen Konsequenzen von der speziellen Relativitätstheorie abweichen und dadurch die Möglichkeit geben, eventuelle Abweichungen vorauszusagen bzw. theoretisch zu interpretieren. Dazu gehören die bereits ältere Testtheorie von Robertson-Mansouri-Sexl (1977), und die immer mehr an Bedeutung gewinnende Standardmodellerweiterung mit einer noch weit größeren Anzahl von Parametern, welche andere Testtheorien in sich einschließt.
Status
Die spezielle Relativitätstheorie ist durch viele Experimente bestätigt worden. Trotz großer Anstrengungen ist es bislang nicht gelungen, Verletzungen der Lorentzinvarianz experimentell zu bestimmen. Sollten diese in Zukunft gefunden werden, so können diese nur im bisher experimentell kaum zugänglichen Bereich der Planck-Skala angesiedelt sein.
Einzelnachweise
- Jakob Laub: Über die experimentellen Grundlagen des Relativitätsprinzips. In: Jahrbuch der Radioaktivität und Elektronik. Bd. 7, 1910, ZDB-ID 533845-1, S. 405–463.
- Yuan Zhong Zhang: Special Relativity and Its Experimental Foundations (= Advanced Series on Theoretical Physical Science. Bd. 4). World Scientific, Singapore u. a. 1997, ISBN 981-02-2749-3.
- David Mattingly: Modern Tests of Lorentz Invariance. In: Living Reviews in Relativity. Bd. 8, Nr. 5, 2005, doi:10.12942/lrr-2005-5.
- Clifford M. Will: Special Relativity: A Centenary Perspective. In: Thibault Damour, Olivier Darrigol, Bertrand Duplantier, Vincent Rivasseau (Hrsg.): Einstein, 1905–2005. Poincaré Seminar 2005 (= Progress in Mathematical Physics. Bd. 47). Birkhäuser, Basel u. a. 2006, ISBN 3-7643-7435-7, S. 33–58, arxiv:gr-qc/0504085.
- Tom Roberts, Siegmar Schleif: What is the experimental basis of Special Relativity?. In: Usenet Physics FAQ. University of California, Riverside. 2007. Abgerufen am 10. Dezember 2014.
- Claus Lämmerzahl: Special Relativity and Lorentz Invariance. In: Annalen der Physik. Bd. 14, Nr. 1/3 = Special Issue Albert Einstein, 2005, S. 71–102, doi:10.1002/andp.200410127.
- Howard P. Robertson: Postulate versus Observation in the Special Theory of Relativity. In: Reviews of Modern Physics. Bd. 21, Nr. 3, 1949, S. 378–382, doi:10.1103/RevModPhys.21.378.
- Aous A. Abdo u. a.: A limit on the variation of the speed of light arising from quantum gravity effects. In: Nature. Bd. 462, Nr. 7271, 2009, S. 331–334, doi:10.1038/nature08574, arxiv:0908.1832, PMID 19865083.