Zwillingsparadoxon

Das Zwillingsparadoxon, auch Uhrenparadoxon, ist ein Gedankenexperiment, das einen scheinbaren Widerspruch in der speziellen Relativitätstheorie beschreibt. Im Gedankenexperiment fliegt ein Zwilling mit nahezu Lichtgeschwindigkeit zu einem fernen Stern, während der andere Zwilling auf der Erde zurückbleibt. Anschließend kehrt der reisende Zwilling mit derselben Geschwindigkeit wieder zurück. Nach der Rückkehr zur Erde stellt sich heraus, dass der dort zurückgebliebene Zwilling älter ist als der Gereiste. Dies ist eine Folge der Zeitdilatation.

Die Höhe des Altersunterschieds zwischen den Zwillingen bei der Rückkehr wird durch die Geschwindigkeit der Reise und durch die zurückgelegte Entfernung bestimmt. Die Reisegeschwindigkeit nahe der Lichtgeschwindigkeit bewirkt zusammen mit den astronomischen Entfernungen zum fernen Stern einen Altersunterschied von mitunter vielen Jahren. Die Zeitdilatation tritt zwar auch bei kleinen Geschwindigkeiten und Entfernungen auf, jedoch ist dann der Zeitunterschied entsprechend kleiner. Im Alltag ist bei den dort auftretenden Geschwindigkeiten und Entfernungen der Unterschied vernachlässigbar klein.

Das Zwillingsparadoxon als Folge der Zeitdilatation

Gemäß der relativistischen Zeitdilatation geht eine Uhr, die zwischen zwei synchronisierten Uhren von A nach B bewegt wird, gegenüber diesen Uhren nach. Albert Einstein wies im Jahre 1905 darauf hin, dass das auch der Fall ist, wenn die Uhr zum Ausgangspunkt zurückkehrt. Das bedeutet, dass eine Uhr, die sich von einem beliebigen Punkt entfernt und dorthin zurückkehrt, gegenüber einer am Ausgangspunkt zurückgelassenen unbewegten Uhr nachgeht.[1] 1911 dehnte Einstein diese Überlegung auf lebende Organismen aus:

„Wenn wir z. B. einen lebenden Organismus in eine Schachtel hineinbrächten und ihn dieselbe Hin- und Herbewegung ausführen liessen wie vorher die Uhr, so könnte man es erreichen, dass dieser Organismus nach einem beliebig langen Fluge beliebig wenig geändert wieder an seinen ursprünglichen Ort zurückkehrt, während ganz entsprechend beschaffene Organismen, welche an den ursprünglichen Orten ruhend geblieben sind, bereits längst neuen Generationen Platz gemacht haben. Für den bewegten Organismus war die lange Zeit der Reise nur ein Augenblick, falls die Bewegung annähernd mit Lichtgeschwindigkeit erfolgte! Dies ist eine unabweisbare Konsequenz der von uns zugrunde gelegten Prinzipien, die die Erfahrung uns aufdrängt.“

– Albert Einstein: Die Relativitäts-Theorie[2]

Die Zeitdilatation selbst ist gemäß dem Relativitätsprinzip symmetrisch. Das heißt, jeder muss die Uhr des anderen als bewegt und somit deren Gangrate als verlangsamt betrachten können. Daraus ergibt sich die Frage, warum die am selben Ort verharrende Uhr nicht aus Sicht der zurückkehrenden Uhr beim Zusammentreffen nachgeht. Das würde einen Widerspruch ergeben, denn beim Zusammentreffen können die Zeigerstellungen beider Uhren nicht jeweils gegenüber der anderen nachgehen. Diese Problemstellung wurde 1911 von Paul Langevin korrekt beantwortet. 1911/13 gelang es Max von Laue, die Erklärung von Langevin mit Hilfe von Minkowski-Diagrammen klarer und anschaulicher darzustellen.[3][4][5]

Das Paradoxon beruht auf intuitiven, aber unzulässigen Annahmen über das Wesen der Zeit, wie beispielsweise der Gleichzeitigkeit. Insbesondere wird dabei der Richtungswechsel am Umkehrpunkt der Reise ignoriert. Durch diese Umkehr sind die beiden Bezugssysteme, in denen die Zwillinge jeweils ruhen, nicht gleichwertig, sondern das Bezugssystem des reisenden Zwillings ist aufgrund der Richtungsumkehr kein Inertialsystem, wodurch sich für ihn die Beurteilung der Gleichzeitigkeit der relevanten Ereignisse ändert. Damit der reisende Zwilling sich während der Hin- und während der Rückreise in einem Inertialsystem befindet, müsste er im Moment der Richtungsumkehr sein Bezugssystem wechseln. Für den anderen, auf der Erde verweilenden Zwilling ändert sich durch die Richtungsumkehr des reisenden Zwillings hingegen nichts, sodass bei diesem die Betrachtung der reinen Zeitdilatation das richtige Endergebnis liefert. Für den Altersunterschied der Zwillinge ist neben der Relativgeschwindigkeit die zwischen den Richtungsänderungen zurückgelegte Distanz von Bedeutung. Da die Dauer der Beschleunigung während der Umkehr im Vergleich zur Reisezeit bei gleichförmiger Bewegung beliebig klein gehalten werden kann, ist diese Dauer der Beschleunigung (im Gegensatz zur Tatsache, dass die Beschleunigung überhaupt stattgefunden hat) von vernachlässigbarer Bedeutung für die Größe des Altersunterschieds. So liefert auch der Fall, bei dem beim Umkehrpunkt lediglich die Uhrzeit per Funksignal auf einen anderen, in entgegengesetzter Richtung reisenden Beobachter übertragen wird, dasselbe Ergebnis wie im Fall mit vernachlässigbar kurzer Dauer der Beschleunigung.

In der Relativitätstheorie werden Raum und Zeit zur sogenannten Raumzeit vereinigt. Jeder Reisende beschreibt in ihr eine Kurve, genannt Weltlinie, deren Länge proportional zur Zeit ist, die für ihn dabei vergeht (die Eigenzeit des Reisenden). Im flachen Raum ist eine gerade Strecke im Raum die kürzeste Verbindung zwischen zwei Punkten, die ein Reisender zurücklegen kann. Ein unbeschleunigter Beobachter bewegt sich auf einer Geraden durch die flache Raumzeit. Das heißt, sowohl der reisende Zwilling als auch der zurückbleibende Zwilling bewegt sich auf einer geraden Linie durch die Raumzeit von dem anfänglichen Raumzeitpunkt weg. Die Länge der Linien ist die Zeit, die der jeweilige Zwilling misst. Um sich an einem Raumzeitpunkt in der Zukunft wieder zu treffen, muss einer der Zwillinge seine Bewegungsrichtung ändern, sodass er sich danach auf einer anderen Geraden durch die Raumzeit bewegt, die sich mit der Weltlinie des anderen Zwillings schneidet. Im euklidischen Raum ist die Gesamtlänge der Linie mit Richtungsumkehr immer länger als die Gerade zwischen den beiden Punkten. Durch die Minkowski-Metrik der flachen Raumzeit, bei der die Orts- und Zeitkoordinaten mit umgekehrtem Vorzeichen beitragen, ist die Gesamtlänge der Linie mit Richtungsumkehr in der flachen Raumzeit immer betragsmäßig geringer als die Länge der geraden Linie, der gereiste Zwilling daher jünger. Würden beide Zwillinge Richtungsänderungen vornehmen, müssten für den Altersunterschied die zurückgelegten Distanzen auf den Weltlinien verglichen werden.[6]

Experimenteller Nachweis

Der Nachweis der Zeitdilatation ist in Teilchenbeschleunigern Routine. Auch eine Zeitdifferenz in der Art des Zwillingsparadoxons (also mit Hin- und Rückflug) wurde bei Speicherringen, wo Myonen mehrmals auf einer kreisförmigen Bahn zum Ausgangsort zurückkamen, nachgewiesen. Durch den Vergleich von Atomuhren konnte dieser Effekt auch in Verkehrsflugzeugen in bester Übereinstimmung mit der Vorhersage der Relativitätstheorie nachgewiesen werden. Bei diesem Hafele-Keating-Experiment, einem Test der aus der Relativitätstheorie folgenden Zeitdilatation, spielen jedoch auch die Erdrotation und Effekte der allgemeinen Relativitätstheorie eine Rolle.[7]

Auflösung des Zwillingsparadoxons

Zur Auflösung des Zwillingsparadoxons im Detail sind folgende zwei Fragen zu beantworten:

Wie kommt es, dass jeder Zwilling den jeweils anderen langsamer altern sieht?
Wieso erweist sich der auf der Erde zurückgebliebene Zwilling nach der Reise als der ältere?

Das wechselseitig langsamere Altern der Zwillinge

Zur Beantwortung der ersten Frage betrachte man, wie der Zwilling auf der Erde überhaupt feststellt, dass der fliegende langsamer altert. Dazu vergleicht er die Anzeige auf einer Uhr, die der fliegende Zwilling mit sich führt, mit zwei ruhenden Uhren, die sich am Anfang und am Ende einer bestimmten Teststrecke befinden, die der fliegende Zwilling passiert. Dazu müssen diese beiden Uhren aus der Sicht des ruhenden Zwillings natürlich auf die gleiche Zeit eingestellt worden sein. Der fliegende Zwilling liest zwar bei den Passagen dieselben Uhrstände ab wie der ruhende, er wird aber einwenden, dass seiner Ansicht nach die Uhr am Ende der Teststrecke im Vergleich zu der am Anfang vorgeht. Der gleiche Effekt tritt auf, wenn der fliegende Zwilling analog das Altern des irdischen mit zwei Uhren beurteilt.

Ursache ist der Umstand, dass es nach der Relativitätstheorie keine absolute Gleichzeitigkeit gibt. Die Gleichzeitigkeit von Ereignissen an verschiedenen Orten und damit auch die angezeigte Zeitdifferenz von zwei dortigen Uhren wird von Beobachtern, die sich mit verschiedenen Geschwindigkeiten bewegen, unterschiedlich beurteilt. Eine genaue Betrachtung der Verhältnisse zeigt, dass die wechselseitige Einschätzung einer Verlangsamung der Zeit daher nicht zu einem Widerspruch führt. Hilfreich sind dazu die vergleichsweise anschaulichen Minkowski-Diagramme, über die sich dieser Sachverhalt grafisch und ohne Formeln nachvollziehen lässt.

Die wechselseitige Verlangsamung steht in Einklang mit dem Relativitätsprinzip, das besagt, dass alle Beobachter, die sich mit konstanter Geschwindigkeit gegeneinander bewegen, völlig gleichberechtigt sind. Man spricht von Inertialsystemen, in denen sich diese Beobachter befinden.

Variante mit Beschleunigungsphasen

Zur Beantwortung der zweiten Frage sind die Abbrems- und die Beschleunigungsphase zu betrachten, die für die Rückkehr des fliegenden Zwillings erforderlich sind. Während dieser beiden Phasen vergeht nach Einschätzung des fliegenden Zwillings die Zeit auf der Erde schneller. Der dort zurückgebliebene Zwilling altert dabei soweit nach, dass er trotz des langsameren Alterns während der Phasen mit konstanter Geschwindigkeit im Endergebnis der Ältere ist, sodass sich auch aus der Sicht des fliegenden Zwillings kein Widerspruch ergibt. Das Ergebnis nach der Rückkehr steht auch nicht im Widerspruch zum Relativitätsprinzip, da die beiden Zwillinge aufgrund der Beschleunigung, die nur der fliegende erfährt, bezüglich der Gesamtreise nicht als gleichwertig betrachtet werden können.

Ursache dieser Nachalterung ist wiederum die Relativität der Gleichzeitigkeit. Während der Beschleunigung wechselt der fliegende Zwilling gewissermaßen ständig in neue Inertialsysteme. In jedem dieser Inertialsysteme ergibt sich jedoch für den Zeitpunkt, der gleichzeitig auf der Erde herrscht, ein anderer Wert und zwar derart, dass der fliegende Zwilling auf eine Nachalterung des irdischen schließt. Je weiter sich die Zwillinge voneinander entfernt haben, umso größer ist dieser Effekt. ( $\Delta \tau =\Delta v\cdot x'/c^{2}$ mit $\Delta v$ als Relativgeschwindigkeit und $x'=x\gamma$ „ursprüngliche“ Entfernung im unbeschleunigten System).

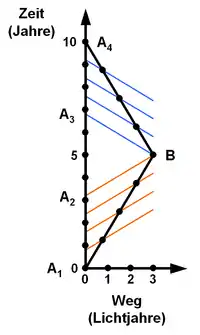
Weg-Zeit-Diagramm für v = 0,6 c. Der Zwilling auf der Erde bewegt sich auf der Zeitachse von A₁ nach A₄. Der reisende Zwilling nimmt den Weg über B. Linien der Gleichzeitigkeit aus der Sicht des reisenden Zwillings sind für die Hinreise rot und für die Rückreise blau eingezeichnet. Die Punkte auf den Reisewegen markieren jeweils ein Jahr Eigenzeit.

Die Verhältnisse sind im dargestellten Weg-Zeit-Diagramm einer Reise von A nach B und wieder zurück mit 60 % der Lichtgeschwindigkeit $c$ dargestellt. Die Bahn des zurückbleibenden Zwillings verläuft entlang der Zeitachse von A₁ nach A₄, der fliegende nimmt den Weg über B. Jede horizontale Linie im Diagramm entspricht Ereignissen, die aus der Sicht des Zwillings auf der Erde gleichzeitig erfolgen. Der fliegende Zwilling dagegen schätzt beim Hinflug alle Ereignisse auf den roten Linien als gleichzeitig ein und beim Rückflug die auf den blauen. Unmittelbar vor seiner Ankunft am Ziel B befindet sich der ruhende Zwilling nach Ansicht des fliegenden daher bei A₂ und erscheint daher weniger gealtert. Während der Umkehrphase, die hier als so kurz angenommen wurde, dass sie im Diagramm nicht zu erkennen ist, schwenken die Linien der Gleichzeitigkeit für den fliegenden Zwilling, und sein Bruder auf der Erde altert bis zum Punkt A₃ nach. Während der Rückreise nach A₄ scheint der Zwilling auf der Erde wieder langsamer zu altern. Da die dargestellten Neigungen der Linien der Gleichzeitigkeit nur von der Reisegeschwindigkeit vor und nach der Umkehrphase abhängen, ist die Stärke der Beschleunigung für die Nachalterungszeit nicht relevant.

Der irdische Zwilling spürt von seiner scheinbaren Nachalterung nichts. Es handelt sich hierbei, wie beschrieben, um einen Effekt im Rahmen der speziellen Relativitätstheorie, der aus einer Darstellung der Vorgänge in unterschiedlichen Koordinatensystemen resultiert, zwischen denen der reisende Zwilling wechselt.

Auch der reisende Zwilling kann den beschriebenen Nachalterungssprung des irdischen Zwillings nicht direkt beobachten, sondern einen solchen lediglich anhand der eingehenden Licht- oder Funksignale in Verbindung mit dem Wissen über die Entfernung, die Relativgeschwindigkeit und die Ausbreitungsgeschwindigkeit des Lichtes erschließen. (Ein Bordcomputer könnte diese Aufgabe übernehmen und die jeweils als gleichzeitig erachtete Zeit auf der Erde anzeigen; während des Wendens würde die Anzeige sprunghaft vorrücken.) Direkt beobachtbar ist für den reisenden Zwilling nur, dass sich vom Wendepunkt B an die eingehenden Licht- oder Funksignale in ihrer Frequenz und im zeitlichen Abstand geändert haben (vergleiche nachfolgenden Abschnitt „Austausch von Lichtsignalen“). Signale von den Punkten A₂ und A₃ treffen dann erst nach seinem Wendepunkt bei ihm ein – im gleichförmigen Zeittakt, der für die eingehenden Signale während der gesamten Rückflugphase gilt.

Variante ohne Beschleunigungsphasen

Durch Einführen einer dritten Person lässt sich eine Variante des Zwillingsparadoxons formulieren, die völlig ohne Beschleunigungsphasen auskommt. Diese Variante („Drei-Brüder-Ansatz“) wurde von Lord Halsbury und anderen eingeführt.[8][9] Dies kann realisiert werden, wenn Rakete A die Erde in vernachlässigbar geringem Abstand passiert und beide währenddessen ihre Uhren mit Funksignalen abgleichen. Danach passiert Rakete A einen Stern mit gleichbleibender Geschwindigkeit und trifft dort in vernachlässigbar kurzem Abstand auf eine zweite Rakete B, die gleichzeitig den Stern mit einer gleich großen, aber zur Erde gerichteten Geschwindigkeit passiert, wobei A seine Zeit mit Funksignalen auf B überträgt. Wenn nun Rakete B bei der Erde eintrifft, geht auch hier die Raketenuhr gegenüber der Erduhr nach. Die mathematische Behandlung dieses Szenarios und sein Endergebnis sind identisch mit dem zuvor geschilderten. Diese Variante mit drei Personen demonstriert, dass nicht die Dauer der Beschleunigung das Zwillingsparadoxon auflöst (denn diese kann im Vergleich zur inertialen Flugzeit beliebig klein gemacht werden), sondern der Umstand, dass das Geschehen während der Hin- und Rückreise in unterschiedlichen Inertialsystemen stattfindet, in denen die Definition der Gleichzeitigkeit notwendigerweise unterschiedlich ausfällt. Es müssen also immer drei Inertialsysteme vorhanden sein:

$S$ , in dem die Erduhr ruht.
$S'$ , in dem die Raketenuhr während des Hinwegs ruht.
$S''$ , in dem die Raketenuhr während des Rückwegs ruht.

Im Beispiel mit Beschleunigungen wechselt dieselbe Raketenuhr von $S'$ nach $S''$ . Im Beispiel ohne Beschleunigungen bleiben die Raketenuhren in ihren Systemen, und es ist die Information der Uhrzeit am Punkt des Zusammentreffens von A und B, die von $S'$ nach $S''$ wechselt.

Zahlenbeispiel

Für eine Hin- und Rückreise mit 60 % der Lichtgeschwindigkeit zu einem Ziel in 3 Lichtjahren Abstand ergeben sich folgende Verhältnisse (siehe obige Grafik): Aus der Sicht des Zwillings auf der Erde sind für Hin- und Rückweg jeweils 5 Jahre erforderlich. Der Faktor für die Zeitdilatation und die Längenkontraktion beträgt 0,8. Das bedeutet, dass der fliegende Zwilling auf dem Hinweg nur um 5 × 0,8 = 4 Jahre altert. Dieser erklärt sich diesen geringeren Zeitbedarf damit, dass die Wegstrecke sich durch die Längenkontraktion bei seiner Reisegeschwindigkeit auf 3 × 0,8 = 2,4 Lichtjahre verkürzt hat. Da nach seiner Einschätzung auf der Erde die Zeit auch langsamer verstreicht, scheinen auf der Erde unmittelbar vor seiner Ankunft beim fernen Stern lediglich 4 × 0,8 = 3,2 Jahre verstrichen zu sein. Aus der Sicht des Erdenbewohners tritt das Ereignis der Ankunft auf dem fernen Stern jedoch erst 1,8 Jahre später auf. An dieser Stelle tritt aufgrund von intuitiven fehlerhaften Annahmen über Gleichzeitigkeit das Paradoxon auf. Durch den Wechsel der Inertialsysteme während der Umkehrphase verschiebt sich die Wahrnehmung des reisenden Zwillings bezüglich des auf der Erde „gleichzeitigen“ Ereignisses zur Ankunft auf dem Stern um 3,6 Jahre. Zusammen mit den 3,2 Jahren auf dem Rückweg sind also auch aus der Sicht des fliegenden Zwillings auf der Erde insgesamt 10 Jahre verstrichen, während er selbst lediglich um 8 Jahre gealtert ist.

Austausch von Lichtsignalen

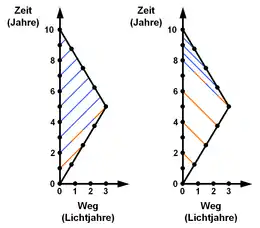
Wege jährlich ausgesandter Lichtsignale. Links Signale, die der irdische Zwilling aussendet und rechts die des Reisenden. Die rot dargestellten empfängt bzw. sendet der Reisende vor der Umkehr und die blauen danach. Aufgrund des Dopplereffekts werden die Signale zunächst mit der halben und später mit der doppelten Frequenz empfangen.

Bisher wurde dargestellt, was die Beobachter unter Berücksichtigung der ihnen bekannten Ausbreitungsgeschwindigkeit des Lichtes für das reale Geschehen halten. Im Folgenden sei beschrieben, was beide Zwillinge unmittelbar sehen, wenn sie einmal pro Jahr ein Lichtsignal zu ihrem Bruder senden. Die Wege von Lichtsignalen im obigen Weg-Zeit-Diagramm sind Geraden mit einem Anstieg von 45° in Senderichtung. Bezogen auf dieses Beispiel ergeben sich die nebenstehenden Diagramme.

Zunächst bewegen sich die Zwillinge voneinander weg, sodass die Lichtstrahlen durch den Dopplereffekt rotverschoben sind. Diese Lichtstrahlen sind im Diagramm rot dargestellt. Nach der Hälfte der Reise bewegen sich die Zwillinge aufeinander zu, sodass die Lichtstrahlen blauverschoben werden, daher sind diese Lichtstrahlen im Bild blau dargestellt. Aufgrund des Relativitätsprinzips messen beide Beobachter die gleichen Zeitintervalle von jeweils 2 Jahren zwischen den roten Signalen und jeweils einem halben Jahr zwischen den blauen Signalen, was im Bild sofort klar wird.

Damit führt die Annahme, beide Zwillinge wären nach der Rückkehr gleich alt, sodass beide Zwillinge gleich viele Signale vom anderen empfangen hätten, nun zu einem Widerspruch. Denn während der reisende Zwilling am Umkehrpunkt und damit nach der halben Reisezeit sofort die zeitlich komprimierten Signale erhält, erreichen den irdischen Zwilling die gedehnten Signale noch länger. Aufgrund des Relativitätsprinzips bekommt also der Beobachter, der für einen längeren Zeitraum blauverschobene Signale erhält, insgesamt mehr Signale als der andere. Der reisende Zwilling bekommt also mehr Signale als der Zwilling auf der Erde, sodass beide übereinstimmend feststellen, dass der reisende Zwilling langsamer gealtert ist.

Im Zahlenbeispiel des nebenstehenden Bildes sieht der reisende Zwilling, bedingt durch eine Kombination von relativistischen Effekten und Laufzeiteffekten, den irdischen zunächst in 4 Jahren um 2 Jahre altern und in weiteren 4 Jahren um 8 Jahre, insgesamt also um 10 Jahre. Der irdische Zwilling sieht entsprechend den Reisenden zunächst in 8 Jahren um 4 Jahre altern und anschließend in 2 Jahren um 4 Jahre, insgesamt also um 8 Jahre.

Beschleunigte Bewegungen

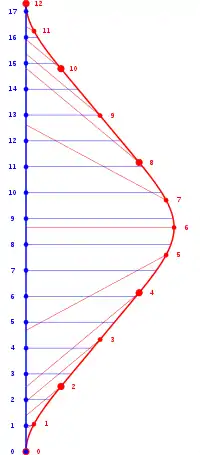
Statt bei der Umkehr eine unendlich hohe Beschleunigung in unendlich kurzer Zeit anzunehmen, ist es mit den Mitteln der speziellen Relativitätstheorie auch möglich, realistischere Bewegungen der Zwillinge mit durchgehend endlicher Beschleunigung zu beschreiben. Oft diskutiert wird dabei der Fall mit konstanter Eigenbeschleunigung (also der Beschleunigung, die der reisende Zwilling mit einem Beschleunigungssensor messen kann), was auch als relativistische Hyperbelbewegung bezeichnet wird.[10][11]

Ein Zwilling soll dabei mit konstanter positiver Eigenbeschleunigung starten, fliegt mit konstanter positiver Geschwindigkeit weiter, kehrt mit konstanter negativer Eigenbeschleunigung um, fliegt weiter mit konstanter negativer Geschwindigkeit, und kommt mit konstanter positiver Eigenbeschleunigung wieder am Anfangsort zum Stillstand. Auf dem Bild wird das folgendermaßen dargestellt: Phase 1 (a=0.6, τ=2); Phase 2 (a=0, τ=2); Phase 3–4 (a=−0.6, 2τ=4); Phase 5 (a=0, τ=2); Phase 6 (a=0.6, τ=2). Hier ist a die Eigenbeschleunigung (in Einheiten, bei denen die Lichtgeschwindigkeit gleich 1 ist) und τ die Eigenzeit des beschleunigten Zwillings. Die dünneren roten Linien sind die Gleichzeitigkeitslinien der momentanen Inertialsysteme, die vom roten Zwilling stetig gewechselt werden. Die dickeren roten Punkte markieren die Zeitpunkte, zu denen der rote Zwilling die Eigenbeschleunigung ändert. Die Zwillinge treffen sich bei T=17.3 und τ=12, der rote Zwilling ist also jünger.

Siehe auch

Bellsches Raumschiffparadoxon

Weblinks

Commons: Zwillingsparadoxon – Sammlung von Bildern, Videos und Audiodateien

Wikibooks: Das »Zwillingsparadoxon« - einmal genau betrachtet – Lern- und Lehrmaterialien

Franz Embacher: Spezielle Relativitätstheorie: Zwillingsparadoxon und Geodäten der Raumzeit.
Klaus Kassner: Crash Course in spezieller Relativitätstheorie: Das Zwillingsparadoxon.
Georg Bernhardt: Zum Zwillingsparadoxon in der Speziellen Relativitätstheorie. (PDF; 340 kB).

Einzelbelege

Albert Einstein: Zur Elektrodynamik bewegter Körper. (PDF) In: Annalen der Physik. 322, Nr. 10, 1905, S. 891–921.
Albert Einstein: Die Relativitäts-Theorie. In: Naturforschende Gesellschaft, Zürich, Vierteljahresschrift. 56, 1911, S. 1–14.
Paul Langevin: L’Évolution de l’espace et du temps. In: Scientia. 10, 1911, S. 31–54.
Max von Laue: Zwei Einwände gegen die Relativitätstheorie und ihre Widerlegung. In: Physikalische Zeitschrift. 13, S. 118–120.
Max von Laue: Das Relativitätsprinzip, 2. Ausgabe. Auflage, Vieweg, Braunschweig 1913.
Arthur I. Miller: Albert Einstein’s special theory of relativity. Emergence (1905) and early interpretation (1905–1911). Addison-Wesley, Reading 1981, ISBN 0-201-04679-2, S. 257–264.
1918 beschrieb Albert Einstein das Paradoxon auch mit Hilfe der Allgemeinen Relativitätstheorie. Siehe
A. Einstein: Dialog über Einwände gegen die Relativitätstheorie. In: Die Naturwissenschaften. Heft 48, S. 697–702 (1918) (Online-PDF).
Talal A. Debs, Michael L. G. Redhead: The twin “paradox” and the conventionality of simultaneity. In: American Journal of Physics. 64, Nr. 4, 1996, S. 384–392. doi:10.1119/1.18252.
Hermann Bondi: Relativity and Common Sense. Doubleday 1964 (Nachdruck Dover 2008, ISBN 0-486-24021-5), S. 80.
T. Müller, A. King, D. Adis: A trip to the end of the universe and the twin “paradox”. In: American Journal of Physics. 76, Nr. 4, 2006, S. 360–373. arxiv:physics/0612126. bibcode:2008AmJPh..76..360M. doi:10.1119/1.2830528.
E. Minguzzi: Differential aging from acceleration: An explicit formula. In: American Journal of Physics. 73, 2005, S. 876–880. arxiv:physics/0411233. doi:10.1119/1.1924490.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Albert Einstein: Zur Elektrodynamik bewegter Körper. (PDF) In: Annalen der Physik. 322, Nr. 10, 1905, S. 891–921.

[2] Albert Einstein: Die Relativitäts-Theorie. In: Naturforschende Gesellschaft, Zürich, Vierteljahresschrift. 56, 1911, S. 1–14.

[3] Paul Langevin: L’Évolution de l’espace et du temps. In: Scientia. 10, 1911, S. 31–54.

[4] Max von Laue: Zwei Einwände gegen die Relativitätstheorie und ihre Widerlegung. In: Physikalische Zeitschrift. 13, S. 118–120.

[5] Max von Laue: Das Relativitätsprinzip, 2. Ausgabe. Auflage, Vieweg, Braunschweig 1913.

[6] Arthur I. Miller: Albert Einstein’s special theory of relativity. Emergence (1905) and early interpretation (1905–1911). Addison-Wesley, Reading 1981, ISBN 0-201-04679-2, S. 257–264.

[7] 1918 beschrieb Albert Einstein das Paradoxon auch mit Hilfe der Allgemeinen Relativitätstheorie. Siehe
A. Einstein: Dialog über Einwände gegen die Relativitätstheorie. In: Die Naturwissenschaften. Heft 48, S. 697–702 (1918) (Online-PDF).

[8] Talal A. Debs, Michael L. G. Redhead: The twin “paradox” and the conventionality of simultaneity. In: American Journal of Physics. 64, Nr. 4, 1996, S. 384–392. doi:10.1119/1.18252.

[9] Hermann Bondi: Relativity and Common Sense. Doubleday 1964 (Nachdruck Dover 2008, ISBN 0-486-24021-5), S. 80.

[10] T. Müller, A. King, D. Adis: A trip to the end of the universe and the twin “paradox”. In: American Journal of Physics. 76, Nr. 4, 2006, S. 360–373. arxiv:physics/0612126. bibcode:2008AmJPh..76..360M. doi:10.1119/1.2830528.

[11] E. Minguzzi: Differential aging from acceleration: An explicit formula. In: American Journal of Physics. 73, 2005, S. 876–880. arxiv:physics/0411233. doi:10.1119/1.1924490.