Michelson-Interferometer

Das Michelson-Interferometer [ˈmaɪkəlsn-] ist ein Interferometer, das nach dem Physiker Albert A. Michelson benannt wurde. Bekanntheit erlangte dieses Messinstrument vor allem durch das Michelson-Morley-Experiment, durch welches der sogenannte Lichtäther als Medium für die Ausbreitung des Lichts untersucht werden sollte. Beim Michelson-Interferometer wird das Phänomen der Interferenz ausgenutzt, welches nur bei kohärentem Licht beobachtet werden kann. Im Normalfall werden also spezielle Lichtquellen, im Regelfall Laser, für Interferenzexperimente eingesetzt. Im Experiment kann es dann mit einem Strahlteiler aufgespalten und schließlich mit sich selbst zur Interferenz gebracht werden. Das Besondere am Michelson-Interferometer ist, dass der Strahlteiler und der teildurchlässige Spiegel, in dem die Strahlen wieder vereinigt werden, derselbe ist.

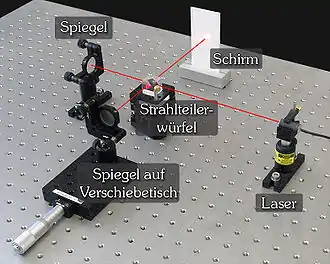
Michelson-Interferometer mit Diodenlaser und eingezeichnetem Strahlengang

Dabei muss der Wegunterschied der überlagerten Wellen kleiner als die Kohärenzlänge sein. Für Medien mit Dispersion und Lichtquellen mit breitem Spektrum wird deswegen eine Korrekturplatte in den Interferometerarm eingebaut. Die Korrekturplatte ist aus dem gleichen Material wie der Strahlteiler und hat dieselbe Dicke, ist aber vollständig lichtdurchlässig. Sie liegt auf der teilenden Seite des Strahlteilers und ist so angebracht, dass der Wegunterschied der beiden Teilstrahlen ausgeglichen wird.

Funktionsweise

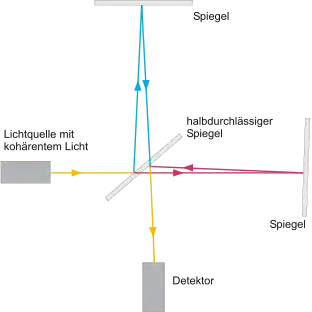
Aufbau des Michelson-Interferometers

Ein Interferometer teilt eine Lichtwelle in zwei Teile auf. Diese zwei Wellen durchlaufen dann unterschiedlich lange Strecken, deren Laufzeit unterschiedlich ist. Es ergibt sich eine Phasenverschiebung zwischen den beiden Wellen. Beim Aufeinandertreffen kommt es zur Interferenz.

Beim Michelson-Interferometer geschieht die Aufteilung der Lichtwelle mittels eines halbdurchlässigen Spiegels. Das von der Lichtquelle ausgehende Licht wird am halbdurchlässigen Spiegel (Strahlteiler) teils durchgelassen (rot markiert), teils jedoch um 90 Grad reflektiert (blau markiert). Das durchgelassene und das reflektierte Licht treffen nun jeweils auf einen (vollständig reflektierenden) Spiegel und werden wieder auf den halbdurchlässigen Spiegel zurückgeworfen. Wieder wird ein Teil reflektiert und ein Teil durchgelassen. Hinter dem halbdurchlässigen Spiegel überlagern sich dann die zwei Wellen (gelb markiert), es kommt zur Interferenz.

Verändert man die optische Weglänge einer der beiden Wellen, z. B. indem man einen der beiden Spiegel verschiebt, oder indem man den Brechungsindex des Mediums in einem der beiden Interferometerarme verändert, so verschieben sich die Phasen der beiden Wellen gegeneinander. Sind sie nun in Phase, so addiert sich ihre Amplitude (man spricht von konstruktiver Interferenz), sind sie jedoch gegenphasig, so löschen sie sich gegenseitig aus (destruktive Interferenz). Über die Intensitätsmessung der resultierenden Welle können bereits kleinste Veränderungen des Gangunterschieds zwischen den beiden Wellen gemessen werden.

Zustandekommen der Interferenzringe

Entstehung der Interferenzringe

Interferenzmuster HeNe-Laser 633 nm

Interferenzmuster Quecksilberdampflampe

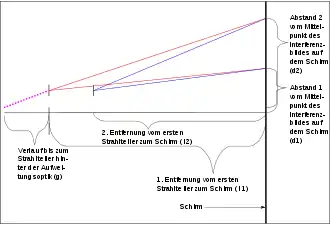
Aus der Lichtquelle kommt ein paralleles Bündel Strahlen (ebene Welle). Dieses wird durch eine Linsenanordnung „aufgeweitet“ und verläuft danach divergent (auseinandergehend) mit einem neuen gedachten Ursprungspunkt G (Kugelwelle), der im Bereich der Linsenanordnung liegt.

Dieses divergente Strahlenbündel wird durch den Strahlteiler in zwei divergente Strahlenbündel aufgeteilt. Die beiden Strahlenbündel werden von je einem Spiegel (je nach Aufbau) reflektiert, wieder zusammengeführt und auf einen Schirm gelenkt. Die Interferenzmuster kommen deshalb zustande, weil die direkten Strecken „Strahlteiler-Spiegel 1-Strahlteiler-Schirm“ (l₁) und „Strahlteiler-Spiegel 2-Strahlteiler-Schirm“ (l₂) unterschiedlich lang sind. Vom gedachten Ursprungspunkt G bis zum Strahlteiler ist die Entfernung konstant (g). Wenn zwei Strahlen aus den beiden Strahlenbündeln zur gleichen Zeit am gleichen Ort (Abstand d vom Mittelpunkt der Interferenzringe) auftreffen, dann haben sie verschieden lange Wege w zurückgelegt. Der exakte Weg lässt sich mittels der Gleichung

w={\sqrt {d^{2}+(g+l)^{2}}}

berechnen.

Bei gleicher Entfernung d vom Mittelpunkt der Interferenzringe sind die Wege w₁ und w₂ unterschiedlich lang. Wenn d linear gesteigert wird, dann steigen w₁ und w₂ unterschiedlich schnell. Wird eine ebene Welle betrachtet, erscheint auf dem Schirm bei konstruktiven Interferenzen ein heller Fleck, bei destruktiven bleibt dieser dunkel. Die Interferenzringe sind eine Folge der Gaußstrahlen, die ab einer gegebenen Länge Kugelwellen sind.

Relative Wegmessung

Das Interferometer ist also geeignet, um langsame Änderungen der Weglängendifferenz zwischen den beiden Teilstrahlen zu messen, also zum Beispiel die Positionsänderung eines der undurchlässigen Spiegel, wobei die erreichbare Auflösung in der Größenordnung der halben Wellenlänge des verwendeten Lichts liegt. Bei sichtbarem Laserlicht beträgt die Wellenlänge einige hundert Nanometer.

Zum Messen verschiebt man einen der beiden undurchlässigen Spiegel und zählt die Anzahl der Interferenzminima (oder auch -maxima), die während der Bewegung durchlaufen werden. Jedes Minimum entspricht dann einer Weglängenänderung um eine Wellenlänge, also einer Positionsänderung des Spiegels um eine halbe Wellenlänge. Die absoluten Weglängen oder deren absolute Differenz können nicht gemessen werden, ebenso wenig die Richtung der Bewegung. Die Geschwindigkeit der messbaren Änderung ist durch die erreichbare Zählrate der Minima begrenzt.

Verbesserung der Wegmessung

Ändert sich die Bewegungsrichtung des Spiegels, besteht das Problem, dass an den Extremstellen des Sinus (den hellsten und dunkelsten Stellen des Interferenzmusters) nicht bekannt ist, ob die Bewegung des Spiegels in die gleiche Richtung fortgesetzt oder umgekehrt wird, da beides den gleichen Signalverlauf erzeugen würde. Daher muss in diesem Fall ein zweiter Sensor an einer anderen Stelle so platziert werden, dass sich nie beide Signale gleichzeitig an Extremstellen befinden.

Die Wegmessung durch Michelson-Interferometer zeichnet sich durch eine (je nach Wellenlänge des Lasers) hohe Auflösung und Linearität aus.

Die heutigen Gravitationswellendetektoren stellen die aufwendigste Variante des Michelson-Interferometers zur Weglängenmessung mit beweglich gelagerten Spiegeln dar.

Heterodyne Michelson-Interferometer

Viele heutige Michelson-Interferometer werden als heterodyne Interferometer ausgelegt. Dabei wird in den beiden Armen des Interferometers eine leicht unterschiedliche Frequenz verwendet. Die wieder zusammengeführten Strahlen ergeben damit eine Schwebung im Detektor. Parallel dazu wird ein Teil des Lichts beider Frequenzen in einem Referenzdetektor überlagert, also nicht an den Spiegeln reflektiert. Die eigentliche Messung ist dann ein Messen der Phasendifferenz zwischen der Schwebung am Detektor und der am Referenzdetektor. Da Phasenwinkelmessungen mit deutlich besserer Genauigkeit als die Interpolation des Interferenzsignals eines homodynen Interferometers möglich sind, sind mit heterodynen Michelson-Interferometern schon Auflösungen von 10 pm erreicht worden.[1] Zudem entfällt das oben genannte Problem mit der Richtungsumkehr an Extremstellen, da die Phasenlage der Schwebung bei geeigneter Auslegung über eine längere Strecke zunimmt und über die Phasendifferenz zwischen Signalarm und Referenzdetektor eindeutig bestimmbar ist.

Zur Erzeugung der beiden Wellenlängen werden üblicherweise auf dem Zeeman-Effekt basierende Laser oder ein Akustooptischer Modulator eingesetzt.

Verwendung als Spektrometer

Benutzt man eine breitbandige IR-Quelle und lässt man den Strahl vor dem Detektor durch eine Messküvette mit einer zu messenden Substanz gehen, kann man deren Spektrum erhalten. Um das zu messende Frequenzband zu durchfahren, muss man dazu die Position des einen Spiegels x, beispielsweise mit einem Piezo-Element, zeitlich ändern, um so verschiedene Gangunterschiede und so Resonanz- und Extinktionsfall bei verschiedenen Wellenlängen zu erzeugen. Die Fourier-Transformation des Interferograms vom Orts- I(x) bzw. Zeitbereich I(t) in den Frequenzbereich $I(\nu )$ liefert das Spektrum der Substanz.

Bestimmung des Brechungsindex eines Gases

Um den Brechungsindex eines Gases zu ermitteln, bringt man eine mit dem entsprechenden Gas gefüllte Küvette in den Teilstrahl, dessen Weglänge zuvor variiert wurde (die Spiegel bleiben jetzt fest). Mit einer an diese Küvette angeschlossenen Pumpe lässt sich der Gasdruck und damit die Anzahl der Gasmoleküle, durch die das Licht hindurch dringt, variieren. Beschreibt man den linearen Zusammenhang zwischen Druck und Brechungsindex als

n(p)=n(0)+{\frac {\Delta n}{\Delta p}}\,p

und nutzt, dass der Anstieg des Brechungsindex durch

{\frac {\Delta n}{\Delta p}}={\frac {\Delta N}{\Delta p}}\,{\frac {\lambda }{2s}}

ausgedrückt werden kann, führt dies zu (n = 1 bei p = 0):

n(p)=1+{\frac {\Delta N}{\Delta p}}\,{\frac {\lambda }{2s}}\,p

Hier bezeichnen N die Anzahl der Intensitätsmaxima im Interferenzmuster, p den Gasdruck, $\lambda$ die Wellenlänge des verwendeten Laserlichtes und s die geometrische Weglänge der Küvette.

Messung der Wellenlängen

Die beiden Strahlbündel sind dabei noch immer kohärent, wenn ihr optischer Wegunterschied kleiner als die Kohärenzlänge der Lichtquelle ist. Sind die Abstände zwischen der semipermeablen Platte und den Spiegeln jeweils gleich, haben die am Detektor eintreffenden Strahlen einen Phasenunterschied von 0. Verschiebt man nun einen der beiden Spiegel um den Abstand $d$ , so entsteht zwischen den beiden Strahlenbündeln ein Wegunterschied $\Delta w=2d$ , und die Lichtstärke ändert sich.

Stellt man nun die Anzahl $z$ der Interferenzmaxima bei einer Verschiebestrecke $\Delta d$ fest, so lässt sich die Wellenlänge $\lambda$ leicht berechnen, da stets gilt:

\Delta d={\frac {\lambda }{2}}z.

Weblinks

Commons: Michelson interferometer – Sammlung von Bildern, Videos und Audiodateien

Bestimmen einer Längenänderung (Memento vom 22. Juni 2006 im Internet Archive) (Real-Video 6,9 MB)
Prinzip der FTIR-Spektroskopie
Selbstbau-Anleitung von der Ligo-Webseite
Michelson Interferometer mit einzelnen Photonen
Benoît Delcourt: Optics – Simulations pour Cours de Physique. Universität Paris XI; abgerufen am 6. November 2021 (englisch, Software zur vollständigen Simulation der wichtigsten Interferometriegeräte).

Einzelnachweise

John Lawall, Ernest Kessler: Michelson interferometry with 10 pm accuracy. In: Review of Scientific Instruments. Band 71, Nr. 7, 2000, S. 2669–2676, doi:10.1063/1.1150715.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] John Lawall, Ernest Kessler: Michelson interferometry with 10 pm accuracy. In: Review of Scientific Instruments. Band 71, Nr. 7, 2000, S. 2669–2676, doi:10.1063/1.1150715.