Sagnac-Interferometer

Ein Sagnac-Interferometer ist ein Interferometer, das es ermöglicht, eine Rotationsgeschwindigkeit absolut zu messen. Ein Beobachter ist in der Lage, anhand dieser Anordnung zu bestimmen, ob er sich in Rotation befindet oder nicht.

Das steht nicht im Widerspruch zum Relativitätsprinzip. Dieses besagt nur die Unmöglichkeit der Bestimmung der gleichförmig translatorischen Eigenbewegung des Beobachters, sofern die dazu benutzte Experimentalanordnung als Ganzes im selben Inertialsystem ruht wie der Beobachter. Die bekannteste Bestätigung dieser Auffassung ist das Michelson-Morley-Experiment, mit dem die gleichförmig translatorische Eigenbewegung der Erde „absolut“ gemessen werden sollte, das jedoch ein negatives Resultat erbrachte. Gleichförmig translatorische Bewegung ist also relativ. Bei Drehbewegungen ist dies jedoch anders. Rotationen gegenüber einem Inertialsystem können auch mit einer geschlossenen Experimentalanordnung absolut gemessen werden, denn es ist nicht möglich, ein Inertialsystem zu definieren, in dem sich die gesamte Experimentalanordnung in Ruhe befindet.

Die älteste Methode zur absoluten Rotationsmessung ist das Foucaultsche Pendel, mit dem es erstmals gelang, die Rotation der Erde ohne Himmelsbeobachtungen zu messen und damit das heliozentrische Weltbild des Nikolaus Kopernikus zu bestätigen. Auch Kreiselkompasse und Laserkreisel funktionieren nach diesem Prinzip. Was das Foucaultsche Pendel für die Mechanik ist, ist der Sagnac-Effekt für die Optik. Zwischen zwei Strahlen von kohärentem Licht, die im Uhrzeigersinn und im Gegenuhrzeigersinn über Spiegel auf derselben Strecke im Kreis gelenkt werden, tritt eine Phasenverschiebung auf, wenn sich die gesamte Apparatur einschließlich der Lichtquelle dreht. Der Weg des Strahls, der in Rotationsrichtung des Geräts umläuft, ist verlängert, der des anderen verkürzt, und zwar proportional zur Rotationsgeschwindigkeit des Geräts.

Dies bestätigt alle Theorien, in welchen die Lichtgeschwindigkeit unabhängig von der Geschwindigkeit des rotierenden Körpers ist – dazu gehören die Spezielle Relativitätstheorie und die Theorie vom ruhenden Lichtäther (wobei die Übereinstimmung zwischen den beiden Theorien nur bei geringen Geschwindigkeiten gegeben ist). Da jedoch die klassische Äthertheorie durch zahlreiche andere Experimente (vor allem dem Michelson-Morley-Experiment) widerlegt wurde, sind die Spezielle Relativitätstheorie und die mit ihr experimentell äquivalente, jedoch konzeptionell überholte lorentzsche Äthertheorie die einzigen Theorien, die alle Experimente erklären können.

Geschichte

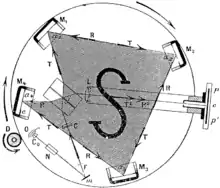
Originalskizze des Sagnac-Interferometers von Georges Sagnac

Erste Hypothesen für das Vorhandensein eines solchen Effektes wurden von Oliver Lodge (1897) und Albert A. Michelson (1904) vorgetragen. Zwei Lichtstrahlen, welche in entgegengesetzter Richtung eine kreisförmige Bahn beschreiben, müssten aufgrund der Erdrotation unterschiedliche Laufzeiten benötigen, was als Verschiebung der Interferenzstreifen nachzuweisen sein müsste. Damit sollte festgestellt werden, ob die Erde den Äther, eine hypothetische Substanz, welche nach den damaligen Vorstellungen den Raum ausfüllen sollte,

mitführt, was ein negatives Resultat ergeben sollte,
oder ob der Äther ruht, was ein positives Resultat ergeben sollte.[1][2][3]

1911 führte Max von Laue diese theoretische Untersuchung weiter, wobei er bereits die spezielle Relativitätstheorie berücksichtigte. Das Ergebnis seiner Berechnungen war, dass sowohl gemäß der speziellen Relativitätstheorie als auch nach der Theorie des ruhenden Lichtäthers bei erster Näherung in $v/c$ annähernd dieselbe Laufzeitdifferenz zu erwarten ist, und zwar aufgrund der Unabhängigkeit der Lichtgeschwindigkeit von der Bewegung der Experimentalanordnung in beiden Theorien. Nur bei vollständiger Äthermitführung (wobei diese Theorie allerdings zu diesem Zeitpunkt aufgrund des Fizeau-Experimentes bereits als widerlegt galt) ergäbe sich ein negatives Resultat.[4][5] Während Laue den Effekt aus Sicht eines beliebigen Inertialsystems herleitete, was für eine widerspruchsfreie Erklärung des Effekts im Rahmen der SRT durchaus ausreichend ist, wurde von anderen Autoren wie Paul Langevin (1921/35) der Effekt auch aus der Sicht eines mitrotierenden Bezugssystems, sowohl gemäß der speziellen als auch der allgemeinen Relativitätstheorie, geschildert.

1913 wurde ein solches Experiment nun tatsächlich von Georges Sagnac durchgeführt, und zwar mit der aus Sicht der Relativitätstheorie (und des ruhenden Äthers) bereits erwarteten Verschiebung der Interferenzstreifen. Sagnac sah den Effekt als Widerlegung der Quellenabhängigkeit der Lichtgeschwindigkeit, d. h. als Widerlegung der Emissionstheorie des Lichtes, und als unmittelbaren Nachweis eines Lichtäthers an – die Relativitätstheorie erwähnte er allerdings nicht.[6][7] Diese Auslassung war jedoch bedeutungslos, da, wie erwähnt, Laue bereits zwei Jahre zuvor einen solchen Effekt als Konsequenz der speziellen Relativitätstheorie vorausgesagt hatte.[8]

Wie erst später bekannt wurde, war bereits zwischen 1909 und 1911 ein ähnliches Experiment von Franz Harress durchgeführt worden, das als eine Synthese der Fizeau- und Sagnac-Experimente betrachtet werden kann. Er versuchte den Mitführungskoeffizienten in Glas zu messen, jedoch benutzte er eine rotierende Versuchsanordnung, welche sehr ähnlich der später von Sagnac benutzten ist. Die von ihm gefundenen Verschiebungen wurden von Harress nicht korrekt interpretiert, jedoch konnte Laue 1920 zeigen, dass das von Harress gefundene Ergebnis dem Sagnac-Effekt entsprach.[9]

Der Aufbau

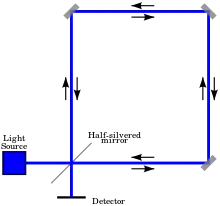
Prinzipaufbau eines Sagnac-Interferometers

Ein kohärentes Lichtbündel einer Lichtquelle, Sagnac verwendete eine Quecksilberdampflampe, wird mit einem halbdurchlässigen Spiegel in zwei Teilstrahlen aufgeteilt. Diese werden mit Hilfe von Spiegeln in entgegengesetzter Richtung im Kreis geführt und treffen an dem Strahlteiler wieder aufeinander. Das Interferenzmuster wird auf einem Detektorschirm beobachtet. Befindet sich die Anordnung in Ruhe, sind die Wege beider Strahlen gleich lang und in der Mitte des Schirms sieht man destruktive Interferenz, denn bei der Reflexion von optisch dünnerem zu optisch dichterem Medium entsteht jeweils eine Phasenverschiebung von 90°, was bei dem im Bild gegen den Uhrzeigersinn laufenden Strahl eine Phasenverschiebung von 180° gegenüber dem im Uhrzeigersinn laufenden Strahl ergibt. Wird nun aber der ganze Aufbau um eine Achse senkrecht zur Strahlebene gedreht, ist der optische Weg für beide Teilstrahlen nicht mehr gleich lang, da sich in der Zeit, die das Licht für einen Umlauf benötigt, der Strahlteiler bereits ein Stück weiter gedreht hat. Dadurch sieht man eine Verschiebung der Interferenzstreifen.

Bemerkenswert an diesem Versuch ist vor allem, dass alle Teile des Systems – Lichtquelle, Zwischenapparat und Messgerät (Beobachter) – mitbewegt werden, man aber trotzdem einen Einfluss der Rotation beobachtet.[10]

Theorie

In jedem Inertialsystem breitet sich Licht mit konstanter Geschwindigkeit $c$ aus. Im Folgenden ist das Inertialsystem das Bezugssystem, und das Interferometer dreht sich mit der Winkelgeschwindigkeit $\Omega$ . Licht läuft auf einer beliebig geformten geschlossenen Bahn der Länge $l$ um. Es wird entsprechend durch Spiegel abgelenkt. Die Zeit, die das Licht benötigt, um die Strecke $\mathrm {d} l$ zurückzulegen, beträgt

\mathrm {d} t={\frac {\mathrm {d} l}{c}}

Während dieser Zeit dreht sich die Apparatur um den Winkel $\Omega \cdot \mathrm {d} t$ . Das Licht muss also unter der Annahme $\Omega \cdot r\ll c$ in Tangentialrichtung ein um

\mathrm {d} x=\Omega \cdot r\cdot \mathrm {d} t={\frac {\Omega \cdot r}{c}}\mathrm {d} l

längeres bzw. kürzeres Wegstück zurücklegen. ( $r$ ist nicht der Abstand zwischen der Drehachse und dem Streckenstück $\mathrm {d} l$ , sondern der Abstand zwischen der Drehachse und der an $\mathrm {d} l$ anliegenden Tangente. $\Omega \cdot r$ ist daher die in Tangentialrichtung zeigende Komponente der Rotationsgeschwindigkeit.) Für den kompletten Umlauf ergibt sich also

x=\oint {\mathrm {d} x}=\oint {{\frac {\Omega \cdot r}{c}}\mathrm {d} l}={\frac {\Omega }{c}}\oint {r\,\mathrm {d} l}={\frac {\Omega }{c}}\cdot 2A

,

wobei $A$ die vom Strahlengang eingeschlossene Fläche ist. Die Differenz der Strecken, die die beiden umlaufenden Lichtwellen zurücklegen müssen, beträgt $2x$ , da eine um $x$ mehr Weg zurücklegt, die andere um $x$ weniger. Die Streifenverschiebung (Gangunterschied als Phasendifferenz) ist damit

\Delta \phi ={\frac {2\pi }{\lambda }}\cdot 2x={\frac {8\pi A}{\lambda c}}\Omega

.

Bei einer Fläche A = 1 m² (in der Skizze mit S bezeichnet) und einer Wellenlänge λ = 633 nm benötigt man eine Winkelgeschwindigkeit $\Omega$ von 1360 °/s (227 Umdrehungen pro Minute), um von destruktiver zu konstruktiver Interferenz ( $\Delta \phi =\pi$ ) zu wechseln.

Michelson-Gale-Versuch

1925 gelang es Albert A. Michelson und Henry G. Gale mit einem Interferometer von 613 m Länge und 339 m Breite nach diesem Prinzip die Rotation der Erde mit einer relativen Genauigkeit von 2 % zu messen. Die relative Streifenverschiebung betrug 0,23. Um scharfe Interferenzstreifen zu erhalten, war der komplette Lichtweg auf 17 mbar evakuiert. Für ausreichend Licht sorgte ein Kohle-Lichtbogen. Das Besondere beim Michelson-Gale-Experiment ist, dass es – anders als beim rotierenden Sagnac-Interferometer – keine Relativbewegung zum Bezugssystem der Erde gibt.[11][12]

Michelson und Gale erkannten bereits selbst korrekt, dass ihr Experiment keine Aussage über die Existenz des Äthers macht. Es lässt sich sowohl mit der Relativitätstheorie als auch mit einem ruhenden Äther erklären. Das Michelson-Gale-Experiment ist aber insofern von großer Bedeutung, als es allen Versuchen, das negative Ergebnis des Michelson-Morley-Experiments durch eine Mitführung des Äthers zu erklären, den Boden entzieht. Es erscheint nämlich widersinnig, dass bei Translation (Michelson-Morley-Versuch) volle Mitführung des Äthers durch die Erde stattfindet, bei Rotation (Michelson-Gale-Versuch) hingegen der Äther relativ zu den Fixsternen ruht.[13]

Siehe auch

Tests der speziellen Relativitätstheorie

Einzelnachweise

Anderson, R., Bilger, H.R., Stedman, G.E.: Sagnac effect: A century of Earth-rotated interferometers. In: Am. J. Phys.. 62, Nr. 11, 1994, S. 975–985. doi:10.1119/1.17656.
Lodge, Oliver: Experiments on the Absence of Mechanical Connexion between Ether and Matter. In: Phil. Trans. Roy. Soc.. 189, 1897, S. 149–166.
Michelson, A. A.: Relative Motion of Earth and Aether. In: Philosophical Magazine. 8, Nr. 48, 1904, S. 716–719.
Pauli, Wolfgang: Die Relativitätstheorie. In: Encyclopädie der mathematischen Wissenschaften, Band 5.2 1921, S. 539–776.
Laue, Max von: Über einen Versuch zur Optik der bewegten Körper. In: Münchener Sitzungsberichte. 1911, S. 405–412.
Sagnac, Georges: L’éther lumineux démontré par l’effet du vent relatif d’éther dans un interféromètre en rotation uniforme. In: Comptes Rendus. 157, 1913, S. 708–710.
Sagnac, Georges: Sur la preuve de la réalité de l’éther lumineux par l’expérience de l’interférographe tournant. In: Comptes Rendus. 157, 1913, S. 1410–1413.
Witte, Hans: Der Sagnac-Effekt: ein Experimentum crucis zugunsten des Äthers?; Nochmals Sagnac-Effekt und Äther; Sagnac-Effekt und Emissionstheorie. In: Berichte der Deutschen Physikalischen Gesellschaft. 16, 1914, S. 142–150, 754–755, 755–756.
Laue, Max von: Zum Versuch von F. Harreß. In: Annalen der Physik. 367, Nr. 13, 1920, S. 448–463.
Siehe G. Joos, Lehrbuch der theoretischen Physik, 12. Auflage 1959, Seite 448
Albert A. Michelson: The Effect of the Earth’s Rotation on the Velocity of Light I. In: The Astrophysical Journal. 61, 1925, S. 137–139. bibcode:1925ApJ....61..137M. doi:10.1086/142878.
Albert A. Michelson & Henry G. Gale: The Effect of the Earth’s Rotation on the Velocity of Light II. In: The Astrophysical Journal. 61, 1925, S. 140–145. bibcode:1925ApJ....61..140M. doi:10.1086/142879.
Siehe Georg Joos: Lehrbuch der theoretischen Physik. 12. Auflage 1959, Seite 450.

Literatur

J. Anandan: Sagnac effect in relativistic and nonrelativistic physics. Phys. Rev. D 24, 338–346 (1981), doi:10.1103/PhysRevD.24.338

Weblinks

Mathpages: The Sagnac Effect

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Anderson, R., Bilger, H.R., Stedman, G.E.: Sagnac effect: A century of Earth-rotated interferometers. In: Am. J. Phys.. 62, Nr. 11, 1994, S. 975–985. doi:10.1119/1.17656.

[2] Lodge, Oliver: Experiments on the Absence of Mechanical Connexion between Ether and Matter. In: Phil. Trans. Roy. Soc.. 189, 1897, S. 149–166.

[3] Michelson, A. A.: Relative Motion of Earth and Aether. In: Philosophical Magazine. 8, Nr. 48, 1904, S. 716–719.

[4] Pauli, Wolfgang: Die Relativitätstheorie. In: Encyclopädie der mathematischen Wissenschaften, Band 5.2 1921, S. 539–776.

[5] Laue, Max von: Über einen Versuch zur Optik der bewegten Körper. In: Münchener Sitzungsberichte. 1911, S. 405–412.

[6] Sagnac, Georges: L’éther lumineux démontré par l’effet du vent relatif d’éther dans un interféromètre en rotation uniforme. In: Comptes Rendus. 157, 1913, S. 708–710.

[7] Sagnac, Georges: Sur la preuve de la réalité de l’éther lumineux par l’expérience de l’interférographe tournant. In: Comptes Rendus. 157, 1913, S. 1410–1413.

[8] Witte, Hans: Der Sagnac-Effekt: ein Experimentum crucis zugunsten des Äthers?; Nochmals Sagnac-Effekt und Äther; Sagnac-Effekt und Emissionstheorie. In: Berichte der Deutschen Physikalischen Gesellschaft. 16, 1914, S. 142–150, 754–755, 755–756.

[9] Laue, Max von: Zum Versuch von F. Harreß. In: Annalen der Physik. 367, Nr. 13, 1920, S. 448–463.

[10] Siehe G. Joos, Lehrbuch der theoretischen Physik, 12. Auflage 1959, Seite 448

[11] Albert A. Michelson: The Effect of the Earth’s Rotation on the Velocity of Light I. In: The Astrophysical Journal. 61, 1925, S. 137–139. bibcode:1925ApJ....61..137M. doi:10.1086/142878.

[12] Albert A. Michelson & Henry G. Gale: The Effect of the Earth’s Rotation on the Velocity of Light II. In: The Astrophysical Journal. 61, 1925, S. 140–145. bibcode:1925ApJ....61..140M. doi:10.1086/142879.

[13] Siehe Georg Joos: Lehrbuch der theoretischen Physik. 12. Auflage 1959, Seite 450.