Kaufmann-Bucherer-Neumann-Experimente

Die Kaufmann-Bucherer-Neumann-Experimente (1901–1915) überprüften die Abhängigkeit der trägen Masse (oder des Impulses) von Elektronen von ihrer Geschwindigkeit. In der Frühzeit der Entwicklung der speziellen Relativitätstheorie hatten diese Experimente eine große Bedeutung für die Anerkennung dieser damals neuen Theorie. Die Ergebnisse dieser Experimente waren lange Zeit umstritten und konnten erst Jahrzehnte nach ihrer erstmaligen Durchführung im Sinne der speziellen Relativitätstheorie vollständig verifiziert werden (vgl. Tests der relativistischen Energie-Impuls-Beziehung und allgemein Tests der speziellen Relativitätstheorie).

Figur 1. Kaufmanns Apparat zur Messung des Ladung-Masse-Verhältnisses und somit zur Abhängigkeit der Masse bzw. des Impulses von Betastrahlung von ihrer Geschwindigkeit. Eine Radiumquelle emittiert Licht durch einen evakuierten Apparat. Parallele magnetische und elektrische Felder lenken die Elektronen ab, bis sie eine photographischen Platte erreichen. a) Frontansicht; b) Seitenansicht; c) Elektronenkurven

Vorgeschichte

Henri Becquerel entdeckte 1896 den radioaktiven Zerfall einer Vielzahl von chemischen Elementen. Danach wurde die dabei entstehende Betastrahlung entdeckt, welche als Emission von negativ geladenen Teilchen interpretiert wurde. Später wurden diese Teilchen mit dem Elektron identifiziert, das 1897 durch Joseph John Thomsons Experimente an Kathodenstrahlen nachgewiesen wurde.

Damit verbunden war die theoretische Herleitung der sogenannten elektromagnetischen Masse durch J. J. Thomson (1881[1]). Demnach vergrößert elektromagnetische Energie die Masse eines Körpers scheinbar. Thomson (1893) und George Frederick Charles Searle (1897[2] ) berechneten auch, dass diese elektromagnetische Masse von der Geschwindigkeit abhängt, und unendlich groß wird, wenn eine elektrische Ladung sich mit Lichtgeschwindigkeit relativ zum Äther bewegt. Auch Hendrik Antoon Lorentz (1899, 1900[3]) konnte eine solche Geschwindigkeitsabhängigkeit als eine Konsequenz seiner Elektronentheorie herleiten. Zu diesem Zeitpunkt wurde die elektromagnetische Masse als „scheinbare Masse“, und die unveränderliche newtonsche Masse als „wahre Masse“ bezeichnet.[A 1][A 2]

Die (transversale) elektromagnetische Masse $m_{T}$ entsprach dem später entwickelten Konzept der „relativistischen Masse“, wobei letztere neben der elektromagnetischen Energie auch für alle anderen Energieformen gültig ist. Diese Massenkonzepte werden allerdings kaum noch benutzt. Stattdessen wird die relativistische Energie bzw. Impuls angewendet, die ebenfalls die Unerreichbarkeit der Lichtgeschwindigkeit (Formelzeichen c) für massive Teilchen beinhalten, denn es gilt:

{\frac {m_{T}}{m}}={\frac {p}{mv}}={\frac {E}{mc^{2}}}={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}

Deswegen können die Kaufmann-Bucherer-Neumann-Experimente auch als frühe Tests der relativistischen Energie-Impuls-Beziehung aufgefasst werden. (Nachfolgend werden aus historischen Gründen weiterhin die Begriffe „transversale“ oder „relativistische Masse“ benutzt.)

Die Experimente von Kaufmann

Erste Experimente

Figur 2. Kaufmanns Messungen von 1901 (korrigiert 1902) zeigten die Abnahme des Ladung-Masse-Verhältnisses mit der Geschwindigkeit. Dabei gilt

\epsilon /m_{0}\sim 1{,}76\times 10^{7}

emu/gm für annähernd ruhende Elektronen.

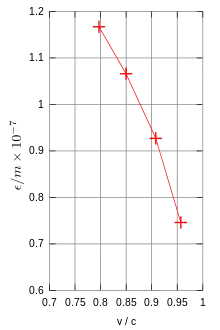
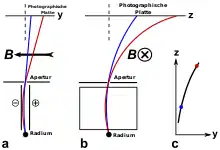
Mit den damals üblichen Kathodenstrahlen hätte maximal 0,3c erreicht werden können, deswegen benutzte Walter Kaufmann Betastrahlung (früher als „Becquerelstrahlen“ bezeichnet) mit Geschwindigkeiten von über 0,9c für seine Experimente. Dabei diente der Zerfall von Radium in einer evakuierten Röhre als Elektronenquelle (Fig. 1). Durch Anwendung von elektrischen und magnetischen Feldern wurde das Ladung-Masse-Verhältnis der Teilchen gemessen. Diese Felder waren parallel zueinander ausgerichtet, wodurch die von ihnen verursachten Ablenkungen senkrecht aufeinander erfolgten. Der Aufprall der Teilchen auf die photographische Platte erzeugte eine Ablenkungskurve, die zu einer bestimmten Geschwindigkeit und Masse passte. Durch Umkehrung des elektrischen Feldes wurden zwei symmetrische Kurven erzeugt, deren Mittellinie die Richtung der magnetischen Ablenkung festlegte. Da die Elektronenladung unabhängig von Geschwindigkeitsänderungen war, musste eine etwaige Änderung des Ladung-Masse-Verhältnisses e/m das Resultat einer Änderung der Masse oder des Impulses sein.[A 3][A 4]

Kaufmann veröffentlichte seine ersten Ergebnisse 1901 und konnte tatsächlich eine Abnahme des Ladung-Masse-Verhältnisses feststellen. Das kann nur erklärt werden wenn die Masse oder der Impuls sich mit größerer Geschwindigkeit entsprechend erhöht. Basierend auf der von Searle (1897) aufgestellten Formel für die Abhängigkeit der elektromagnetischen Energie von der Geschwindigkeit geladener Körper, definierte Kaufmann die Zunahme der elektromagnetischen Masse als Funktion der Geschwindigkeit:[4]

\phi (\beta )={\frac {3}{4\beta ^{2}}}\left[{\frac {1}{\beta }}\lg {\frac {1-\beta }{1+\beta }}+{\frac {2}{1-\beta ^{2}}}\right],\;\beta ={\frac {v}{c}}

.

Kaufmann bemerkte dass diese Formel die Ergebnisse nicht erklären konnte, deswegen nahm er an, dass die Gesamtmasse der Elektronen überwiegend zur „wahren mechanischen Masse“ gehöre, jedoch nur ein kleinerer Teil gehöre zur „scheinbaren elektromagnetischen Masse“. Er beging jedoch zwei Fehler bei der Auswertung: Einerseits konnte Max Abraham zeigen, dass obige Formel nur in longitudinaler Richtung korrekt ist, jedoch für diese Experimente ist die transversale Richtung entscheidend. Hier gilt bei Annahme des Elektrons als starre Kugel:

\phi (\beta )={\frac {3}{4\beta ^{2}}}\left({\frac {1+\beta ^{2}}{2\beta }}\lg {\frac {1+\beta }{1-\beta }}-1\right)

Andererseits beging Kaufmann einen Rechenfehler bei der Berechnung der Ablenkungskurven. In einer Neuanalyse 1902 korrigierte er diese Fehler und stellte Übereinstimmung mit Abrahams Formel fest.[5]

1902 und 1903 führte Kaufmann weitere Experimente unter verbesserten Bedingungen durch. Die Resultate wurden von ihm als weitere Bestätigung von Abrahams Theorie und als Nachweis des vollständig elektromagnetischen Ursprungs der Masse aufgefasst.[6] [7]

Die Zunahme der Elektronenmasse mit der Geschwindigkeit wurde darüber hinaus durch Hermann Starke bestätigt, der 1903 Experimente mit Kathodenstrahlen von ungefähr 0,3c durchführte.[8]

Konkurrierende Theorien

Figur 3. Voraussagen zur Geschwindigkeitsabhängigkeit der transversalen elektromagnetischen Masse nach Abraham, Lorentz und Bucherer.

1902 veröffentlichte Max Abraham eine Theorie, in welcher das Elektron eine starre Kugel war, deren Ladung gleichmäßig auf ihrer Oberfläche verteilt ist. Wie oben beschrieben, führte er die „transversale elektromagnetische Masse“ zusätzlich zur „longitudinalen elektromagnetischen Masse“ ein. Nach dieser Theorie wäre die gesamte Elektronenmasse elektromagnetischen Ursprungs, während eine mechanische Masse überhaupt nicht mehr existiert.[A 5][A 6][9] [10] [11]

Auch Lorentz (1899, 1904) erweiterte seine Elektronentheorie durch Einführung der Lorentz-Transformation, wobei sich ergab, dass die Elektronen in Bewegungsrichtung einer Verkürzung, der sogenannten Längenkontraktion, unterworfen sind. Dies führte zu Termen für die elektromagnetische Masse, welche von denen von Abraham abwichen. Trotzdem konnte Lorentz zeigen, dass sie mit den kaufmannschen Ergebnisse ebenso gut übereinstimmten wie jene von Abraham. 1905 konnte Henri Poincaré die Theorie von Lorentz weiter entwickeln, sodass sie von nun an mit dem Relativitätsprinzip, d. h., mit der Unmöglichkeit einer Bestimmung einer absoluten, inertialen Bewegung, vollständig übereinstimmte.[A 5][A 7][12] [13]

Eine andere Theorie wurde 1904 von Alfred Bucherer und Paul Langevin entwickelt. Sie unterscheidet von der lorentzschen dadurch, dass zusammen mit der Kontraktion in Bewegungsrichtung eine Dehnung senkrecht dazu auftritt, wodurch das Volumen konstant bleibt.[A 7] [14]

Schließlich entwickelte Albert Einstein 1905 die bis heute gültige spezielle Relativitätstheorie, welche eine Änderung der Masse aufgrund der Lorentz-Transformation zwischen relativ zueinander bewegten Inertialsystemen beinhaltete. Trotz völlig verschiedener Voraussetzungen entsprechen die Vorhersagen dieser Theorie jenen von Lorentz.[A 8][15]

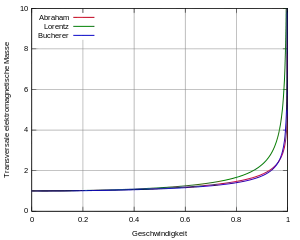
Bezüglich der transversalen Massenzunahme in ergaben sich folgende Voraussagen der jeweiligen Theorie:

{\begin{aligned}&{\text{Abraham}}&\phi (\beta )&={\frac {3}{4\beta ^{2}}}\left({\frac {1+\beta ^{2}}{2\beta }}\lg {\frac {1+\beta }{1-\beta }}-1\right)\\&{\text{Lorentz-Einstein}}&\phi (\beta )&=(1-\beta ^{2})^{-1/2}\\&{\text{Bucherer-Langevin}}&\phi (\beta )&=(1-\beta ^{2})^{-1/3}\end{aligned}}

Experimente von 1905

Um eine Entscheidung zwischen diesen Theorien herbeizuführen, führte Kaufmann seine Experimente abermals mit größerer Präzision durch. Aus dem Vergleich obiger Formeln mit seinen Ergebnissen schloss Kaufmann, dass er die Lorentz-Einstein-Formel, und somit das Relativitätsprinzip, klar widerlegt hätte. Deshalb seien die einzig verbliebenen Theorien jene von Abraham und Bucherer, welche annähernd gleich gut mit den Ergebnissen übereinstimmten. Lorentz war ratlos und schrieb in einem Brief: „ich bin am Ende meines Lateins“.[A 9][A 10][16] [17]

Bereits kurz nachdem Kaufmann seine Ergebnisse und Schlüsse veröffentlicht hatte, wurden diese jedoch durch Max Planck einer neuen Analyse unterworfen.[A 11][A 12] In zwei 1906 und 1907 veröffentlichten Arbeiten konnte er zwar keine experimentelle Fehler oder Rechenfehler finden, doch zeigte er, dass Kaufmanns Ergebnisse nicht vollständig schlüssig seien. So würde sich bei weiterer Extrapolation der Kurven die Möglichkeit von Überlichtgeschwindigkeiten ergeben. Somit würden diese Messungen keine endgültige Entscheidung darstellen.[18][19] Und Einstein gab 1907 zwar zu, dass Kaufmanns Resultate besser zu den Theorien von Abraham und Bucherer passen würden als zu seiner eigenen, jedoch seien die Grundlagen dieser Theorien nicht plausibel und weitgehend genug, sodass sie eine geringe Wahrscheinlichkeit hätten, sich als richtig zu erweisen.[20]

Weitere Experimente

Bucherer

Adolf Bestelmeyer (1906–1907) kritisierte einige technische Aspekte von Kaufmanns Experimenten, besonders die Verwendung von parallelen elektrischen und Magnetfeldern. Deswegen führte er selbst Experimente mit Kathodenstrahlen von ungefähr 0,3c durch. Dabei entwickelte er einen Geschwindigkeitsfilter unter Anwendung von senkrecht zueinander stehenden elektrischen und magnetischen Feldern. Ähnliche Methoden waren bereits vorher von J. J. Thomson und Wilhelm Wien verwendet worden. Dabei erhielt er Resultate für das Ladung-Masse-Verhältnis, die erheblich von denen Kaufmanns abwichen. Bestelmeyer fügte allerdings hinzu, dass seine Daten keine Entscheidung zwischen den Theorien erlaubten.[21]

Deswegen führte Alfred Bucherer 1908 neue Experimente mit Betastrahlen von bis zu 0,7c unter Benutzung eines Geschwindigkeitsfilters, ähnlich dem von Bestelmeyer, durch (Fig. 4 & 5.) Eine Radiumquelle befand sich dabei in der Mitte eines kreisförmigen, geladenen Kondensators, der sich wiederum in einem Magnetfeld befand. Nur bei denjenigen Strahlen, die sich in Richtung α ausbreiteten und eine bestimmte Geschwindigkeit hatten, kompensierten sich Magnet- und elektrische Felder exakt, sodass sie sich geradlinig ausbreiteten. Nachdem die Strahlen den Kondensator verlassen hatten, wurden sie vom Magnetfeld abgelenkt und trafen auf die photographische Platte.[22] [23]

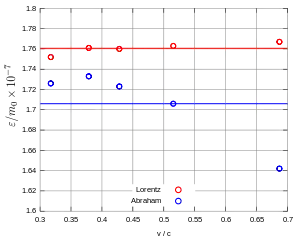
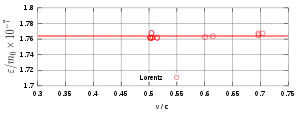
Figure 6. Fünf Datenpunkte bei Bucherers Experiment.

Figure 7. Dreizehn Datenpunkte bei Wolzs Experiment.

Für die Endanalyse benutzte Bucherer die Formeln von Abraham und Lorentz-Einstein, um aus den gemessenen Werten das Ladung-Masse-Verhältnis für ruhende Elektronen zu errechnen. Da dieses Verhältnis im Ruhezustand konstant ist, müssen die Werte alle auf einer Linie liegen (Fig. 6). Das war annähernd nur bei Lorentz-Einstein der Fall, während Abrahams Daten deutlich voneinander abwichen. Deswegen schloss Bucherer, dass die Ergebnisse das Relativitätsprinzip und somit die Relativitätstheorie bzw. die „Lorentz-Einstein-Theorie“ bestätigt hätten. Bucherers Ergebnisse wurden mit Erleichterung und Zufriedenheit von Lorentz, Einstein, und Hermann Minkowski aufgenommen.[A 13][A 14]

Kurt Wolz, ein Student Bucherers, führte weitergehende Experimente durch, in denen er ebenfalls Übereinstimmung mit der Lorentz-Einstein-Formel feststellte (Fig. 7).[24]

Obwohl also die Mehrheit der Physiker Bucherers Ergebnisse akzeptierten, blieben Zweifel bestehen. So gab es, vor allem durch Bestelmeyer, Einwände in Bezug auf die technische Durchführung, welche zu einem polemischen Disput zwischen Bucherer und Bestelmeyer in mehreren Publikationen führte. Bestelmeyer wandte beispielsweise ein, dass ein einzelnes Experiment keine so weitreichenden Schlüsse rechtfertige, dass exakte Datenprotokolle fehlen, und der Einfluss der nicht-kompensierten Strahlen nicht ausgeschlossen werden konnte. Auch Wolzs Experimente hätten seine Einwände nicht entkräftet.[25] [26] [27] [28]

Hupka

Im Gegensatz zu Kaufmann und Bucherer, benutzte Karl Erich Hupka (1909) Kathodenstrahlen von bis zu 0,5c für seine Experimente. Die von einer Kupferkathode erzeugten Strahlen wurden von einem Feld zwischen Anode und Kathode einer evakuierten Entladungsröhre beschleunigt. Die Anode diente dabei als Diaphragma, das von Strahlen mit konstanter Geschwindigkeit passiert wurde, und welches das Schattenbild von zwei Wollaston-Drähten auf einen Phosphoreszenzschirm hinter einem zweiten Diaphragma warf. Wenn ein Strom hinter dem Diaphragma erzeugt wurde, wurden die Strahlen abgelenkt und das Schattenbild verschob sich. Die Daten stimmten mit der Lorentz-Einstein-Formel überein, doch Hupka ergänzte, dass sein Experiment keine definitive Entscheidung bringen konnte.[29] W. Heil veröffentlichte daraufhin einige Arbeiten, in denen er die Ergebnisse analysierte und kritisierte. Hupka nahm dazu Stellung und verteidigte seine Ergebnisse und Methoden.[30][31][32]

Neumann und Guye/Lavanchy

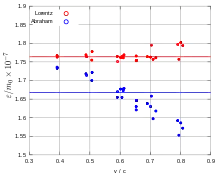
Figur 8. Neumanns Auswertung von 26 Datenpunkten für jede Theorie.

1914 führte Günther Neumann neue Messungen unter Benutzung von Bucherers Apparaten durch, die er weiter verbesserte. Dabei ging er besonders auf Bestelmeyers Einwände ein, wie der Frage nach den nicht-kompensierten Strahlen, und ausgedehnten Datenprotokollen. Sein Experiment ergab, dass auch hier die Daten zum Ladung-Masse-Verhältnis gemäß der Lorentz-Einstein-Formel wie erfordert annähernd auf einer horizontalen Linie waren, während Abrahams Daten eine deutlich Kurve aufwiesen (Fig. 8). Neumann schloss, dass seine Experimente mit denen von Bucherer und Hupka übereinstimmten, die Lorentz-Einstein-Formel endgültig bestätigt hätten in dem Bereich 0,4–0,7c, und Abrahams Formel endgültig widerlegt hätten. Da Instrumentalfehler im Bereich von 0,7–0,8c auftraten, ist die in diesem Bereich gefundene Abweichung von der Lorentz-Einstein-Formel nicht signifikant.[33]

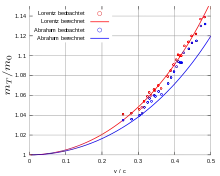
Figur 9. Guye und Lavanchys Auswertung von 25 Datenpunkten für jede Theorie.

1915 beobachteten Charles-Eugène Guye und Charles Lavanchy die Ablenkung von Kathodenstrahlen bei Geschwindigkeiten von 0,25–0,5c. In einer Röhre mit einer Kathode und einer Anode wurden die Strahlen beschleunigt. Das Diaphragma an der Anode erzeugte den Strahl, der daraufhin abgelenkt wurde. Die Strahlen schlugen auf einen Schirm, an dem die Treffer mit einer Kamera photographiert wurden. Danach berechneten sie das Verhältnis aus transversaler elektromagnetischer Masse m_T und „Ruhemasse“ m₀ und fanden Übereinstimmung mit der Lorentz-Einstein-Formel (Fig. 9). Dadurch wurde Neumanns Ergebnis auch bei geringeren Geschwindigkeiten bestätigt.[34][35]

Diese Experimente wurden als schlüssige Bestätigungen der Lorentz-Einstein-Formel aufgefasst, sodass Lorentz 1915 schreiben konnte:[A 15]

Spätere Experimente […] haben die Formel […] für die transversale elektromagnetische Masse bestätigt, sodass aller Wahrscheinlichkeit nach, der einzige Einwand der gegen die Hypothese des deformierbaren Elektrons und des Relativitätsprinzips gemacht werden konnte, nun beseitigt ist.

Weitere Entwicklungen

Figur 10. Elektrostatischer Spektrograph von Rogers et al.

Jahrzehnte später argumentierten allerdings Zahn und Spees (1938)[36] und Faragó und L. Jánossy (1957),[37] dass viele Annahmen bezüglich der Natur der Elektronen bzw. den Eigenschaften der Experimentalanordnung, welche von den damaligen Experimentatoren gemacht wurden, sehr ungenau waren. Die Bucherer-Neumann-Experimente hätten genauso wie Kaufmanns Messungen lediglich eine qualitative Zunahme des Impulses bzw. der Masse gezeigt, die keineswegs genau genug waren, um zwischen den konkurrierenden Theorien zu entscheiden.[A 16][A 17]

Während also diese Experimente lange Zeit umstritten waren, lieferten die Studien über die Feinstruktur der Wasserstofflinien durch Karl Glitscher bereits 1917 eine klare Bestätigung der Lorentz-Einstein-Formel, und eine Widerlegung aller Konkurrenztheorien. Zur Herleitung der Feinstruktur sind nämlich die genauen Werte für relativistische Energie und Impuls notwendig, was mit Abrahams Formel nicht möglich ist.[38][A 18]

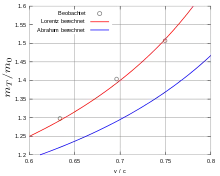
Figur 11. Drei Datenpunkte von Rogers et al., in Übereinstimmung mit der Lorentz-Einstein-Formel.

Um auch bei Elektronenablenkungsexperimenten eine endgültige Entscheidung herbeizuführen, führten Rogers et al. (1940) mit verbesserter Ausstattung neue Experimente durch. Die Zerfallsreihe von Radium ergibt ein Spektrum von Betastrahlen mit einem weiten Energiebereich. Die früheren Messungen von Kaufmann, Bucherer oder Neumann benutzten flache, parallele Plattenkondensatoren, die keine Fokussierung der Betateilchen ermöglichten. Rogers et al. (Fig. 10) benutzten hingegen einen elektrostatischen Spektrographen, der eine genaue Fokussierung ermöglichte. Der Spektrograph wurde aus zwei Segmenten von zwei Zylindern konstruiert und war von einem evakuierten Eisenkasten umschlossen. Die Betastrahlen wurden von einem feinen Platindraht erzeugt der mit aktivem Radium beschichtet war. Die Strahlen trafen auf eine Spalt vor einem Geigerzähler. Die Analyse ergab, dass die Messpunkte auf der Kurve für das Verhältnis von transversaler Masse und Ruhemasse gemäß der Lorentz-Einstein-Formel war (Fig. 11). Es wurde dabei eine Genauigkeit von 1 % erreicht, wodurch Abrahams Theorie ausgeschlossen war.[39]

Moderne Tests

Heute ist die genaue Bestätigung der speziellen Relativitätstheorie in Teilchenbeschleunigern bereits Routine, s. Tests der relativistischen Energie-Impuls-Beziehung

Literatur

Michel Janssen, Matthew Mecklenburg: From classical to relativistic mechanics: Electromagnetic models of the electron. In: V. F. Hendricks, et al. (Hrsg.): Interactions: Mathematics, Physics and Philosophy. Springer, Dordrecht 2007, S. 65–134.

Hendrik Antoon Lorentz: The theory of electrons and its applications to the phenomena of light and radiant heat. B. G. Teubner, Leipzig/Berlin 1916.

Arthur I. Miller: Albert Einstein's special theory of relativity. Emergence (1905) and early interpretation (1905–1911). Addison-Wesley, Reading 1981, ISBN 0-201-04679-2.

Abraham Pais: Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford University Press, 1982/2005, ISBN 0-19-280672-6.

Wolfgang Pauli: Die Relativitätstheorie. In: Encyclopädie der mathematischen Wissenschaften. 5, Nr. 2, 1921, S. 539–776.

Richard Staley: Einstein's generation. University Press, Chicago 2008, ISBN 0-226-77057-5.

Weblinks

Präsentation zu Kaufmanns Experiment (PowerPoint; 1,3 MB)
Schleif Roberts: What is the experimental basis of Special Relativity? 2006 (Experimentelle Tests der SRT).

Einzelnachweise

Sekundärquelle

Siehe Miller 1981, S. 45–47.
Siehe Pais 2005, S. 155–159
Siehe Miller 1981, S. 47–54.
Siehe Staley 2008, S. 223–233.
Siehe Miller 1981, S. 55–67.
Siehe Staley 2008, S. 229–233.
Siehe Janssen 2007, Abschnitt 4
Siehe Staley 2008, S. 241–242
Siehe Miller 1981, S. 228–232.
Siehe Staley 2008, S. 242–244
Siehe Miller 1981, S. 232–235
Siehe Staley 2008, S. 244–250
Siehe Miller 1981, S. 345–350.
Siehe Staley 2008, S. 250–254.
Siehe Lorentz 1916, S. 339. „Later experiments […] have confirmed the formula […] for the transverse electromagnetic mass, so that, in all probability, the only objection that could be raised against the hypothesis of the deformable electron and the principle of relativity has now been removed.“
Siehe Miller 1981, S. 351–352
Siehe Janssen 2007, Abschnitt 7.
Siehe Pauli 1921, S. 636–637

Primärquellen

J. J. Thomson: On the Effects produced by the Motion of Electrified Bodies. In: Philosophical Magazine. 11, Nr. 68, 1881, S. 229–249.
G. F. C. Searle: On the Steady Motion of an Electrified Ellipsoid. In: Philosophical Magazine. 44, Nr. 269, 1897, S. 329–341.
H. A. Lorentz: Über die scheinbare Masse der Ionen. In: Physikalische Zeitschrift. 2, Nr. 5, 1900, S. 78–80.
W. Kaufmann: Die magnetische und elektrische Ablenkbarkeit der Bequerelstrahlen und die scheinbare Masse der Elektronen. In: Göttinger Nachrichten. Nr. 2, 1901, S. 143–168.
W. Kaufmann: Über die elektromagnetische Masse des Elektrons. In: Göttinger Nachrichten. Nr. 5, 1902, S. 291–296.
W. Kaufmann: Die elektromagnetische Masse des Elektrons. In: Physikalische Zeitschrift. 4, Nr. 1b, 1902, S. 54–56.
W. Kaufmann: Über die "Elektromagnetische Masse" der Elektronen. In: Göttinger Nachrichten. Nr. 3, 1903, S. 90–103.
H. Starke: Über die elektrische und magnetische Ablenkung schneller Kathodenstrahlen. In: Verhandlungen der Deutschen Physikalischen Gesellschaft. Nr. 13, 1903, S. 241–250.
M. Abraham: Dynamik des Electrons. In: Göttinger Nachrichten. 1902, S. 20–41.
M. Abraham: Prinzipien der Dynamik des Elektrons. In: Physikalische Zeitschrift. 4, Nr. 1b, 1902, S. 57–62.
M. Abraham: Prinzipien der Dynamik des Elektrons. In: Annalen der Physik. 10, 1903, S. 105–179.
Hendrik Antoon Lorentz: Elektromagnetische Erscheinungen in einem System, das sich mit beliebiger, die des Lichtes nicht erreichender Geschwindigkeit bewegt. In: Otto Blumenthal, Arnold Sommerfeld (Hrsg.): Das Relativitätsprinzip. Eine Sammlung von Abhandlungen (1913) 1904, S. 6–26.
Henri Poincaré: Sur la dynamique de l’électron. In: Rendiconti del Circolo matematico di Palermo. 21, S. 129–176. Siehe auch deutsche Übersetzung.
A. H. Bucherer: Mathematische Einführung in die Elektronentheorie. Teubner, Leipzig 1904, S. 57.
Albert Einstein: Zur Elektrodynamik bewegter Körper. In: Annalen der Physik. 322, Nr. 10, 1905, S. 891–921. doi:10.1002/andp.19053221004.
Walter Kaufmann: Über die Konstitution des Elektrons. In: Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften. 45, 1905, S. 949–956.
Walter Kaufmann: Über die Konstitution des Elektrons. In: Annalen der Physik. 324, Nr. 3, 1906, S. 487–553.
Max Planck: Die Kaufmannschen Messungen der Ablenkbarkeit der β-Strahlen in ihrer Bedeutung für die Dynamik der Elektronen. In: Physikalische Zeitschrift. 7, 1906, S. 753–761.
M. Planck: Nachtrag zu der Besprechung der Kaufmannschen Ablenkungsmessungen. In: Verhandlungen der Deutschen Physikalischen Gesellschaft. Band 9, Nr. 14, 1907, S. 301–305.
Albert Einstein: Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen. In: Jahrbuch der Radioaktivität und Elektronik. 4, 1908, S. 411–462.
A. Bestelmeyer: Spezifische Ladung und Geschwindigkeit der durch Röntgenstrahlen erzeugten Kathodenstrahlen. In: Annalen der Physik. 327, Nr. 3, 1907, S. 429–447. doi:10.1002/andp.19073270303.
A. H. Bucherer: Messungen an Becquerelstrahlen. Die experimentelle Bestätigung der Lorentz-Einsteinschen Theorie. In: Physikalische Zeitschrift. 9, Nr. 22, 1908, S. 755–762.
A. H. Bucherer: Die experimentelle Bestätigung des Relativitätsprinzips. In: Annalen der Physik. 333, Nr. 3, 1909, S. 513–536. doi:10.1002/andp.19093330305.
Kurt Wolz: Die Bestimmung von e/m0. In: Annalen der Physik. 335, Nr. 12, 1909, S. 273–288. doi:10.1002/andp.19093351206.
A. H. Bestelmeyer: Bemerkungen zu der Abhandlung Hrn. A. H. Bucherers: Die experimentelle Bestätigung des Relativitätsprinzips. In: Annalen der Physik. 335, Nr. 11, 1909, S. 166–174. doi:10.1002/andp.19093351105.
A. H. Bucherer: Antwort auf die Kritik des Hrn. E. Bestelmeyer bezüglich meiner experimentellen Bestätigung des Relativitätsprinzips. In: Annalen der Physik. 335, Nr. 11, 1909, S. 974–986. doi:10.1002/andp.19093351506.
A. H. Bestelmeyer: Erwiderung auf die Antwort des Hrn. A. H. Bucherer. In: Annalen der Physik. 337, Nr. 6, 1910, S. 231–235. doi:10.1002/andp.19103370609.
A. H. Bucherer: Erwiderung auf die Bemerkungen des Hrn. A. Bestelmeyer. In: Annalen der Physik. 338, Nr. 14, 1910, S. 853–856. doi:10.1002/andp.19103381414.
E. Hupka: Beitrag zur Kenntnis der trägen Masse bewegter Elektronen. In: Annalen der Physik. 336, Nr. 1, 1910, S. 169–204. bibcode:1909AnP...336..169H. doi:10.1002/andp.19093360109.
W. Heil: Diskussion der Versuche über die träge Masse bewegter Elektronen. In: Annalen der Physik. 336, Nr. 3, 1910, S. 519–546. bibcode:1910AnP...336..519H. doi:10.1002/andp.19103360305.
E. Hupka: Zur Frage der trägen Masse bewegter Elektronen. In: Annalen der Physik. 338, Nr. 12, 1910, S. 400–402. bibcode:1910AnP...336..519H. doi:10.1002/andp.19103360305.
W. Heil: Zur Diskussion der Hupkaschen Versuche über die träge Masse bewegter Elektronen. In: Annalen der Physik. 338, Nr. 12, 1910, S. 403–413. bibcode:1910AnP...338..403H. doi:10.1002/andp.19103381210.
Günther Neumann: Die träge Masse schnell bewegter Elektronen. In: Annalen der Physik. 350, Nr. 20, 1914, S. 529–579. bibcode:1914AnP...350..529N. doi:10.1002/andp.19143502005.
C. E. Guye, C. Lavanchy: Vérification expérimentale de la formule de Lorentz-Einstein par les rayons cathodiques de grande vitesse. In: Compt. Rend. Acad. Sci.. 161, 1915, S. 52–55.
C. E. Guye, C. Lavanchy: Vérification expérimentale de la formule de Lorentz-Einstein par les rayons cathodiques de grande vitesse. In: Archives des sciences physiques et naturelles. 42, 1915, S. 286ff.
C. T. Zahn, A. A. Spees: A Critical Analysis of the Classical Experiments on the Variation of Electron Mass. In: Physical Review. 53, 1938, S. 511–521. bibcode:1938PhRv...53..511Z. doi:10.1103/PhysRev.53.511.
P. S. Faragó, L. Jánossy: Review of the experimental evidence for the law of variation of the electron mass with velocity. In: Il Nuovo Cimento. 5, Nr. 6, 1957, S. 379–383. doi:10.1007/BF02856033.
Karl Glitscher: Spektroskopischer Vergleich zwischen den Theorien des starren und des deformierbaren Elektrons. In: Annalen der Physik. 357, Nr. 6, 1917, S. 608–630. doi:10.1002/andp.19173570603.
M. M. Rogers et al.: A Determination of the Masses and Velocities of Three Radium B Beta-Particles. In: Physical Review. 57, 1940, S. 379–383. doi:10.1103/PhysRev.57.379.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[4] Siehe Miller 1981, S. 45–47.

[Pais1982_155-5] Siehe Pais 2005, S. 155–159

[6] Siehe Miller 1981, S. 47–54.

[Staley2008_223-7] Siehe Staley 2008, S. 223–233.

[Miller1981_55-13] Siehe Miller 1981, S. 55–67.

[Staley2008_229-14] Siehe Staley 2008, S. 229–233.

[Jassen2005_16-18] Siehe Janssen 2007, Abschnitt 4

[Staley2009_241-22] Siehe Staley 2008, S. 241–242

[24] Siehe Miller 1981, S. 228–232.

[Staley2009_242-25] Siehe Staley 2008, S. 242–244

[28] Siehe Miller 1981, S. 232–235

[Staley2009_244-29] Siehe Staley 2008, S. 244–250

[36] Siehe Miller 1981, S. 345–350.

[Staley2009_250-37] Siehe Staley 2008, S. 250–254.

[50] Siehe Lorentz 1916, S. 339. „Later experiments […] have confirmed the formula […] for the transverse electromagnetic mass, so that, in all probability, the only objection that could be raised against the hypothesis of the deformable electron and the principle of relativity has now been removed.“

[53] Siehe Miller 1981, S. 351–352

[Jassen2005_41-54] Siehe Janssen 2007, Abschnitt 7.

[Pauli1921_636-56] Siehe Pauli 1921, S. 636–637

[1] J. J. Thomson: On the Effects produced by the Motion of Electrified Bodies. In: Philosophical Magazine. 11, Nr. 68, 1881, S. 229–249.

[2] G. F. C. Searle: On the Steady Motion of an Electrified Ellipsoid. In: Philosophical Magazine. 44, Nr. 269, 1897, S. 329–341.

[3] H. A. Lorentz: Über die scheinbare Masse der Ionen. In: Physikalische Zeitschrift. 2, Nr. 5, 1900, S. 78–80.

[8] W. Kaufmann: Die magnetische und elektrische Ablenkbarkeit der Bequerelstrahlen und die scheinbare Masse der Elektronen. In: Göttinger Nachrichten. Nr. 2, 1901, S. 143–168.

[9] W. Kaufmann: Über die elektromagnetische Masse des Elektrons. In: Göttinger Nachrichten. Nr. 5, 1902, S. 291–296.

[10] W. Kaufmann: Die elektromagnetische Masse des Elektrons. In: Physikalische Zeitschrift. 4, Nr. 1b, 1902, S. 54–56.

[11] W. Kaufmann: Über die "Elektromagnetische Masse" der Elektronen. In: Göttinger Nachrichten. Nr. 3, 1903, S. 90–103.

[12] H. Starke: Über die elektrische und magnetische Ablenkung schneller Kathodenstrahlen. In: Verhandlungen der Deutschen Physikalischen Gesellschaft. Nr. 13, 1903, S. 241–250.

[15] M. Abraham: Dynamik des Electrons. In: Göttinger Nachrichten. 1902, S. 20–41.

[16] M. Abraham: Prinzipien der Dynamik des Elektrons. In: Physikalische Zeitschrift. 4, Nr. 1b, 1902, S. 57–62.

[17] M. Abraham: Prinzipien der Dynamik des Elektrons. In: Annalen der Physik. 10, 1903, S. 105–179.

[19] Hendrik Antoon Lorentz: Elektromagnetische Erscheinungen in einem System, das sich mit beliebiger, die des Lichtes nicht erreichender Geschwindigkeit bewegt. In: Otto Blumenthal, Arnold Sommerfeld (Hrsg.): Das Relativitätsprinzip. Eine Sammlung von Abhandlungen (1913) 1904, S. 6–26.

[20] Henri Poincaré: Sur la dynamique de l’électron. In: Rendiconti del Circolo matematico di Palermo. 21, S. 129–176. Siehe auch deutsche Übersetzung.

[21] A. H. Bucherer: Mathematische Einführung in die Elektronentheorie. Teubner, Leipzig 1904, S. 57.

[23] Albert Einstein: Zur Elektrodynamik bewegter Körper. In: Annalen der Physik. 322, Nr. 10, 1905, S. 891–921. doi:10.1002/andp.19053221004.

[26] Walter Kaufmann: Über die Konstitution des Elektrons. In: Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften. 45, 1905, S. 949–956.

[27] Walter Kaufmann: Über die Konstitution des Elektrons. In: Annalen der Physik. 324, Nr. 3, 1906, S. 487–553.

[30] Max Planck: Die Kaufmannschen Messungen der Ablenkbarkeit der β-Strahlen in ihrer Bedeutung für die Dynamik der Elektronen. In: Physikalische Zeitschrift. 7, 1906, S. 753–761.

[31] M. Planck: Nachtrag zu der Besprechung der Kaufmannschen Ablenkungsmessungen. In: Verhandlungen der Deutschen Physikalischen Gesellschaft. Band 9, Nr. 14, 1907, S. 301–305.

[32] Albert Einstein: Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen. In: Jahrbuch der Radioaktivität und Elektronik. 4, 1908, S. 411–462.

[33] A. Bestelmeyer: Spezifische Ladung und Geschwindigkeit der durch Röntgenstrahlen erzeugten Kathodenstrahlen. In: Annalen der Physik. 327, Nr. 3, 1907, S. 429–447. doi:10.1002/andp.19073270303.

[34] A. H. Bucherer: Messungen an Becquerelstrahlen. Die experimentelle Bestätigung der Lorentz-Einsteinschen Theorie. In: Physikalische Zeitschrift. 9, Nr. 22, 1908, S. 755–762.

[35] A. H. Bucherer: Die experimentelle Bestätigung des Relativitätsprinzips. In: Annalen der Physik. 333, Nr. 3, 1909, S. 513–536. doi:10.1002/andp.19093330305.

[38] Kurt Wolz: Die Bestimmung von e/m0. In: Annalen der Physik. 335, Nr. 12, 1909, S. 273–288. doi:10.1002/andp.19093351206.

[39] A. H. Bestelmeyer: Bemerkungen zu der Abhandlung Hrn. A. H. Bucherers: Die experimentelle Bestätigung des Relativitätsprinzips. In: Annalen der Physik. 335, Nr. 11, 1909, S. 166–174. doi:10.1002/andp.19093351105.

[40] A. H. Bucherer: Antwort auf die Kritik des Hrn. E. Bestelmeyer bezüglich meiner experimentellen Bestätigung des Relativitätsprinzips. In: Annalen der Physik. 335, Nr. 11, 1909, S. 974–986. doi:10.1002/andp.19093351506.

[41] A. H. Bestelmeyer: Erwiderung auf die Antwort des Hrn. A. H. Bucherer. In: Annalen der Physik. 337, Nr. 6, 1910, S. 231–235. doi:10.1002/andp.19103370609.

[42] A. H. Bucherer: Erwiderung auf die Bemerkungen des Hrn. A. Bestelmeyer. In: Annalen der Physik. 338, Nr. 14, 1910, S. 853–856. doi:10.1002/andp.19103381414.

[43] E. Hupka: Beitrag zur Kenntnis der trägen Masse bewegter Elektronen. In: Annalen der Physik. 336, Nr. 1, 1910, S. 169–204. bibcode:1909AnP...336..169H. doi:10.1002/andp.19093360109.

[44] W. Heil: Diskussion der Versuche über die träge Masse bewegter Elektronen. In: Annalen der Physik. 336, Nr. 3, 1910, S. 519–546. bibcode:1910AnP...336..519H. doi:10.1002/andp.19103360305.

[45] E. Hupka: Zur Frage der trägen Masse bewegter Elektronen. In: Annalen der Physik. 338, Nr. 12, 1910, S. 400–402. bibcode:1910AnP...336..519H. doi:10.1002/andp.19103360305.

[46] W. Heil: Zur Diskussion der Hupkaschen Versuche über die träge Masse bewegter Elektronen. In: Annalen der Physik. 338, Nr. 12, 1910, S. 403–413. bibcode:1910AnP...338..403H. doi:10.1002/andp.19103381210.

[47] Günther Neumann: Die träge Masse schnell bewegter Elektronen. In: Annalen der Physik. 350, Nr. 20, 1914, S. 529–579. bibcode:1914AnP...350..529N. doi:10.1002/andp.19143502005.

[48] C. E. Guye, C. Lavanchy: Vérification expérimentale de la formule de Lorentz-Einstein par les rayons cathodiques de grande vitesse. In: Compt. Rend. Acad. Sci.. 161, 1915, S. 52–55.

[49] C. E. Guye, C. Lavanchy: Vérification expérimentale de la formule de Lorentz-Einstein par les rayons cathodiques de grande vitesse. In: Archives des sciences physiques et naturelles. 42, 1915, S. 286ff.

[51] C. T. Zahn, A. A. Spees: A Critical Analysis of the Classical Experiments on the Variation of Electron Mass. In: Physical Review. 53, 1938, S. 511–521. bibcode:1938PhRv...53..511Z. doi:10.1103/PhysRev.53.511.

[farago-52] P. S. Faragó, L. Jánossy: Review of the experimental evidence for the law of variation of the electron mass with velocity. In: Il Nuovo Cimento. 5, Nr. 6, 1957, S. 379–383. doi:10.1007/BF02856033.

[55] Karl Glitscher: Spektroskopischer Vergleich zwischen den Theorien des starren und des deformierbaren Elektrons. In: Annalen der Physik. 357, Nr. 6, 1917, S. 608–630. doi:10.1002/andp.19173570603.

[57] M. M. Rogers et al.: A Determination of the Masses and Velocities of Three Radium B Beta-Particles. In: Physical Review. 57, 1940, S. 379–383. doi:10.1103/PhysRev.57.379.