Spinpolarisation

In einer Ansammlung gleichartiger Teilchen wie Elektronen, Atome oder Ionen besteht Spinpolarisation, wenn die Spinvektoren der Teilchen mehr oder weniger ausgerichtet sind, die Richtungen also nicht zufällig verteilt sind. In der Fachsprache z. B. der Kernphysik wird dann meist einfach von Polarisation gesprochen.

Grundlagen

Der Axialvektor eines durch die Quantenzahl $S$ beschriebenen Spins kann gegenüber einer gewählten Quantisierungsachse $2S+1$ verschiedene Richtungen einnehmen (siehe Richtungsquantelung, Multiplizität). Diese werden durch eine "spinmagnetische" Quantenzahl $m_{s}$ bezeichnet:

m_{S}=\underbrace {-S,-S+1,...,S-1,S} _{2S+1\,\mathrm {Werte:\,Multiplizit{\ddot {a}}t} }.

Im einfachsten Fall $S={\tfrac {1}{2}}$ ergeben sich die beiden Werte $m_{s}=-{\tfrac {1}{2}}$ und $m_{s}=+{\tfrac {1}{2}}$ (Multiplizität 2).

Zustände, die sich nur im Wert von $m_{s}$ unterscheiden, sind zwar quantenmechanisch verschieden. Sie haben aber normalerweise gleiche Energie, sind also „entartet“. In einem Ensemble gleichartiger Teilchen sind diese Zustände daher im Allgemeinen bis auf zufällige statistische Schwankungen gleich stark besetzt (eine Ausnahme bilden die Elektronen und Positronen der Betastrahlung, siehe unten).

Eine Polarisation, also Abweichung von der Gleichverteilung, lässt sich bei Spin-1/2-Teilchen beschreiben durch den Polarisationsgrad $P$ :

P={\frac {N_{u}-N_{d}}{N_{u}+N_{d}}}.

Dabei sind $N_{u}$ und $N_{d}$ die Anzahlen der Teilchen mit den beiden Spinausrichtungen („up“ und „down“) zur gewählten Achse. Auch der Polarisationsgrad wird oft kurz als „die Polarisation“ bezeichnet. $P$ beträgt für ein unpolarisiertes Ensemble 0, für ein maximal polarisiertes ±1, häufig als ±100 % ausgedrückt. Auch die Beschreibung durch einen Polarisationsvektor ist möglich; dieser ist die Vektorsumme aller Spins im Ensemble geteilt durch die Teilchenanzahl und wird meist ebenfalls auf den Betrag 1 für maximale Polarisation normiert. Bei Teilchen mit höherem Spin als 1/2, also drei oder mehr möglichen Ausrichtungen, ist die Beschreibung der Polarisation komplizierter und erfordert im Allgemeinen einen Tensor entsprechender Stufe.

Spinpolarisation ist also keine Eigenschaft eines einzelnen Teilchens, sondern des Ensembles. Von einem einzelnen „polarisierten Teilchen“ zu sprechen ist sinnlos. Quantenmechanisch lässt die Spinpolarisation sich mit dem Dichtematrix-Formalismus beschreiben.

Spinpolarisation im Magnetfeld

Der Spin von Teilchen ist mit einem magnetischen Moment verbunden. Bringt man das Teilchenensemble in ein Magnetfeld, ändert sich daher die Energie des einzelnen Zustands je nach Stellung zur Feldrichtung, die Entartung wird aufgehoben. Daher rührt die Bezeichnung "magnetische" Quantenzahl. Die entsprechende beobachtbare Aufspaltung optischer Spektrallinien heißt Zeeman-Effekt.

Da sich die Teilchen bevorzugt in Zuständen kleinerer Energie sammeln, führt das Magnetfeld schon ohne weitere Maßnahmen zu einer gewissen Spinpolarisation. Diese ist allerdings bei Umgebungstemperatur meist gering, weil die magnetischen Energieunterschiede klein sind gegenüber der thermischen Energie der Teilchen (dies gilt insbesondere für Atomkerne mit ihren kleinen magnetischen Momenten). Mit speziellen Verfahren lassen sich weitaus höhere Polarisationen erreichen. Dies wird in manchen,[1] aber nicht allen[2][3] Fällen als Hyperpolarisation bezeichnet.

Spin-Bahn-Wechselwirkung bei Streuprozessen

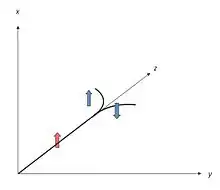
Spin- (rot) und Bahndrehimpulsvektor (blau) bei Streuung nach links oder nach rechts

Wird ein zunächst auf gerader Bahn fliegendes Teilchen mit Spin aus seiner Flugrichtung abgelenkt, beeinflusst die Wechselwirkung zwischen Spin und Bahndrehimpuls die Bewegung, ähnlich wie in Atomen und Atomkernen (siehe Spin-Bahn-Kopplung). Zeigt beispielsweise der Spinvektor in die $x$ -Richtung, während das Teilchen in $z$ -Richtung fliegt, stehen die Vektoren von Spin und Bahndrehimpuls bei Ablenkung (Streuung) in die $y$ -Richtung antiparallel, in die - $y$ -Richtung parallel zueinander (siehe Skizze). Der differentielle Wirkungsquerschnitt ist dadurch bei gleichem Streuwinkel verschieden, je nachdem die Streuung zur + $y$ -Seite oder zur - $y$ -Seite hin erfolgt. Allgemeiner gesagt: er hängt außer vom Streuwinkel auch vom Azimutwinkel (siehe Kugelkoordinaten), dem Winkel zwischen der Bahnebene und der xz-Ebene, ab. Für einen polarisierten Teilchenstrahl stellt der Streuprozess auf diese Weise einen Analysator dar, denn zwei symmetrisch zueinander links und rechts der $xz$ -Ebene aufgestellte Detektoren registrieren verschieden viele Teilchen. Andererseits sind bei unpolarisiertem Strahl die Teilchen, die nach einer bestimmten Seite gestreut werden, ein mehr oder weniger stark polarisiertes Ensemble; der Streuprozess wirkt also auch als Polarisator.

Wegen der Drehimpulserhaltung zeigt sich auch bei Kernreaktionen entsprechendes Verhalten wie bei Streuung. Streu- und Reaktionsexperimente mit Beobachtung der Polarisation der emittierten Teilchen oder mit polarisiertem Strahl oder Target sind daher in der Kernphysik ein wichtiges Mittel zur näheren Bestimmung der Spin-Bahn-Wechselwirkung. Bevor man polarisierte Teilchenstrahlen oder polarisierte Targets herstellen konnte, lieferten Doppelstreuexperimente, bei denen dieselben Teilchen zwei Streuungen nacheinander durchliefen, Informationen dazu.[4] Bei ihnen stellte die erste Streuung den Polarisator, die zweite den Analysator dar.

Mit einem polarisierten 1,16-GeV-Elektronenstrahl ist in einem Streuexperiment die schwache Ladung des Protons genau gemessen worden. Dabei wurde ausgenutzt, dass nur in der schwachen Wechselwirkung die Nichterhaltung der Parität gilt.[5]

Herstellung der Spinpolarisation

Neutrale Materie

In Feststoffen, Flüssigkeiten oder Gasen wird Polarisation der Atomkerne mittels eines Magnetfelds erzeugt, oft mit Hilfe tiefer Temperatur, um die thermische Energie der Teilchen klein zu halten (siehe Boltzmann-Verteilung). Mit dieser Technik wurde z. B. im Wu-Experiment bei 10 Millikelvin ein Polarisationsgrad der Cobalt-60-Kerne von ca. 60 % erreicht.

Statt eines starken äußeren Feldes kann zur Polarisation der Kerne in manchen Fällen das in einem paramagnetischen Ion vom Elektronenspin verursachte Feld ausgenutzt werden,[6] so dass ein relatives schwaches äußeres Feld genügt, das die Ionen ausrichtet.

Eine weitere Methode besteht darin, Atome durch optisches Pumpen mit zirkular polarisiertem Licht auszurichten und die Kopplung der Elektronen mit dem Kernmoment (siehe Hyperfeinstruktur) auszunutzen.

Ionenstrahlen

Polarisierte Ionenstrahlen zur Verwendung in Teilchenbeschleunigern lassen sich nach dem weiterentwickelten Konzept des Stern-Gerlach-Experiments herstellen: aus einem Atomstrahl, z. B. Wasserstoff oder Deuterium, wird im inhomogenen Magnetfeld ein polarisierter Teilstrahl gewonnen und dieser dann – im einfachsten Fall – in einem schwachen Magnetfeld unter Ausnützung der Hyperfeinaufspaltung ionisiert.[7]

Ein anderer Typ „polarisierter Ionenquellen“ nutzt die Aufspaltung der Energieniveaus durch die Lamb-Verschiebung aus.[8]

Elektronenstrahlen

Elektronen in Speicherringen werden durch Emission von Synchrotronstrahlung longitudinal polarisiert.[9]

Neutronen

Polarisierte langsame Neutronen für die Neutronenstreuung werden durch Reflexion an den ausgerichteten Atomen eines ferromagnetischen Spiegels (siehe Neutronensuperspiegel) gewonnen.

Anwendungen

Spinpolarisierte Neutronen können verwendet werden, um die magnetische Struktur von Festkörpern zu untersuchen.
In der Photoelektronenspektroskopie kann die Spinpolarisation der emittierten Elektronen Aufschluss über die magnetische Ausrichtung der Probe und die Polarisation der anregenden Strahlung geben.
In der Kernphysik helfen Streu- und Kernreaktionsexperimente mit polarisierten Teilchen, Einzelheiten bestimmter Zustände der Kerne zu erforschen, da die Wirkungsquerschnitte der Prozesse von der Spinausrichtung abhängen.
Möglicherweise kann die Reaktionsausbeute in Kernfusionsreaktoren durch Verwendung spinpolarisierten Brennstoffs wesentlich verbessert werden.[10]
Substanzen mit polarisierten Atomkernen verbessern bei bestimmten Kernresonanz-Untersuchungen, z. B. in der Medizin, die Empfindlichkeit (siehe Hyperpolarisation (Physik)).
Die spinpolarisierte Rastertunnelmikroskopie ermöglicht detaillierte Untersuchungen der Oberfläche von magnetisierten Materialien.
Eine zeitlich konstante Elektronenpolarisation wird im Lesekopf von Festplatten beim Auslesen über den magnetoresistiven Effekt genutzt. In anfänglichen Modellen betrug diese Polarisation nur wenige Prozent.
Eine zeitlich kohärent oszillierende Elektronenpolarisation ist bei der Rabi-Oszillation in magnetischen Systemen nachweisbar. Sie ist möglicherweise in Quantencomputern verwendbar.

Elektronen- und Positronenpolarisation beim Betazerfall

Die beim Betazerfall emittierten Teilchen sind entlang ihrer Emissionsrichtung spinpolarisiert. Anschaulich gesagt rotieren z. B. die Elektronen aus Beta-Minus-Zerfällen, in ihrer Flugrichtung gesehen, vorzugsweise gegen den Uhrzeigersinn (linkshändige Elektronen). Erklärt wird dies damit, dass die für den Betazerfall verantwortliche schwache Wechselwirkung nur chiral linkshändige Teilchen und chiral rechtshändige Antiteilchen erzeugt, insofern also die Spiegelsymmetrie der Naturgesetze maximal verletzt (siehe Paritätsverletzung). Dies wirkt sich als longitudinale Spinpolarisation der emittierten Teilchen aus. Theorie und Messungen ergeben, dass der Polarisationsgrad $P={v}/{c}$ beträgt ( $v$ Teilchengeschwindigkeit, $c$ Lichtgeschwindigkeit), für relativistische Beta-Elektronen und für Neutrinos aus dem Betazerfall also praktisch 100 %.[11]

Literatur

H. Paetz gen. Schieck: Nuclear Physics with Polarized Particles. Heidelberg usw.: Springer, 2012. ISBN 978-3-642-24225-0.

Einzelnachweise

J. E. Reimer: Nuclear hyperpolarization in solids and the prospects of nuclear spintronics. Solid State Nuclear Magnetic Resonance Bd. 37 (2010) S. 3–12.
z. B. allgemein nicht im Zusammenhang mit Kernreaktionen, siehe etwa Schieck (Literaturliste).
N. Bigelow, P. Nacher and M. Leduc: Accurate optical measurement of nuclear polarization in optically pumped He-3 gas. J. de Physique Bd. 2 (1992) S. 2159–2179.
Bernard L. Cohen, Concepts of Nuclear Physics, New York usw.: McGraw-Hill, 1971, S. 53.
The Jefferson Lab Q-weak Collaboration: Precision measurement of the weak charge of the proton. Nature Bd. 557 (2018) Seite 207–211, doi:10.1038/s41586-018-0096-0 .
E. B. Paul: Nuclear and Particle Physics. Amsterdam: North-Holland, 1969. S. 318
G. Clausnitzer, R. Fleischmann und H. Schopper, Zeitschrift für Physik Band 144 (1956) S. 336.
L. W. Anderson and W. Haeberli (eds.): Polarized Ion Sources and Polarized Gas Targets (Konferenzbericht, Madison, Wisconsin 1993). American Inst. of Physics, 1994.
A. A. Sokolov, I. M. Ternov: On Polarization and Spin Effects in Synchrotron Radiation Theory. Sov. Phys. Dokl. Band 8, S. 1203 (1964).
H. Paetz gen. Schieck: The status of polarized fusion, Eur. Phys. J. 44 A (2010) S. 321–354.
Jörn Bleck-Neuhaus: Elementare Teilchen. Von den Atomen über das Standard-Modell bis zum Higgs-Boson. 2., überarbeitete Auflage. Springer, Berlin Heidelberg 2013. Seite 546 f.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] J. E. Reimer: Nuclear hyperpolarization in solids and the prospects of nuclear spintronics. Solid State Nuclear Magnetic Resonance Bd. 37 (2010) S. 3–12.

[2] z. B. allgemein nicht im Zusammenhang mit Kernreaktionen, siehe etwa Schieck (Literaturliste).

[3] N. Bigelow, P. Nacher and M. Leduc: Accurate optical measurement of nuclear polarization in optically pumped He-3 gas. J. de Physique Bd. 2 (1992) S. 2159–2179.

[4] Bernard L. Cohen, Concepts of Nuclear Physics, New York usw.: McGraw-Hill, 1971, S. 53.

[5] The Jefferson Lab Q-weak Collaboration: Precision measurement of the weak charge of the proton. Nature Bd. 557 (2018) Seite 207–211, doi:10.1038/s41586-018-0096-0 .

[6] E. B. Paul: Nuclear and Particle Physics. Amsterdam: North-Holland, 1969. S. 318

[7] G. Clausnitzer, R. Fleischmann und H. Schopper, Zeitschrift für Physik Band 144 (1956) S. 336.

[8] L. W. Anderson and W. Haeberli (eds.): Polarized Ion Sources and Polarized Gas Targets (Konferenzbericht, Madison, Wisconsin 1993). American Inst. of Physics, 1994.

[9] A. A. Sokolov, I. M. Ternov: On Polarization and Spin Effects in Synchrotron Radiation Theory. Sov. Phys. Dokl. Band 8, S. 1203 (1964).

[10] H. Paetz gen. Schieck: The status of polarized fusion, Eur. Phys. J. 44 A (2010) S. 321–354.

[11] Jörn Bleck-Neuhaus: Elementare Teilchen. Von den Atomen über das Standard-Modell bis zum Higgs-Boson. 2., überarbeitete Auflage. Springer, Berlin Heidelberg 2013. Seite 546 f.