Doppelbrechung

Die Doppelbrechung oder Birefringenz ist die Fähigkeit optisch anisotroper Medien, ein Lichtbündel in zwei senkrecht zueinander polarisierte Teilbündel zu trennen (ordentlicher und außerordentlicher Strahl). Die Ursache dieses Effekts liegt im unterschiedlichen Brechungsindex (n_o und n_ao) in Abhängigkeit von der Ausbreitungsrichtung und der Polarisation des Lichts.

Doppelbrechung beim Calcit

Doppelbrechung an einem Kalkspat-Kristall:
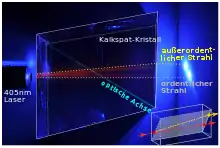
ordentlicher und außerordentlicher Strahl sind durch rote Fluoreszenz im Kristall sichtbar

Ein prominentes Beispiel für ein solches Material ist Calcit (auch Kalkspat oder Doppelspat genannt), an dem die Doppelbrechung 1669 von Erasmus Bartholin entdeckt wurde.

Auch optisch isotrope Materialien (z. B. im kubischen Kristallsystem) können durch äußere Einflüsse doppelbrechend werden. Solche Einflüsse sind z. B.

mechanische Spannung (Deformations- oder Spannungsdoppelbrechung, siehe Spannungsoptik)
Texturen und Eigenspannungen bei der Formgebung
elektrische Felder (elektrische Doppelbrechung, elektrooptischer Kerr-Effekt)
magnetische Felder (magnetische Doppelbrechung, Cotton-Mouton-Effekt, allgemein siehe Magnetooptik)
innere Reibung und damit verbundene Texturen bei Strömungen hochzäher Flüssigkeiten.

Die meisten Flüssigkristalle sind spontan doppelbrechend.

Eng verwandt bzw. verbunden mit der Doppelbrechung ist der Dichroismus, bei dem Farben polarisationsabhängig absorbiert werden.

Physikalische Ursache

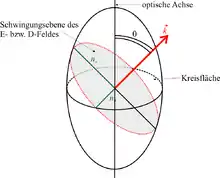
Indexellipsoid eines optisch einachsigen Kristalls

Doppelbrechung tritt in optisch anisotropen Kristallen auf. Diese weisen für unterschiedliche Polarisation und Richtung des eingestrahlten Lichtes einen unterschiedlichen Brechungsindex auf.

Das zugehörige Indexellipsoid kann sein:

optisch einachsig bzw. uniaxial, d. h. eine optische Achse und zwei verschiedene Hauptbrechachsen bzw. Brechungsindizes haben; dies ist der Fall in den wirteligen Kristallsystemen (trigonal, tetragonal und hexagonal)
optisch zweiachsig bzw. biaxial, d. h. zwei optische Achsen und drei verschiedene Hauptbrechachsen bzw. Brechungsindizes haben. Dies ist der Fall im orthorhombischen, monoklinen und triklinen Kristallsystem. Hier sind im Allgemeinen beide gebrochenen Strahlen außerordentlich (elektrisches Feld ${\vec {E}}$ und elektrische Flussdichte ${\vec {D}}$ haben nicht die gleiche Richtung, wobei der Ausbreitungsvektor ${\vec {k}}$ nicht – wie sonst üblich – senkrecht zu ${\vec {E}}$ ist, sondern zu ${\vec {D}}$ , siehe Literatur).

Die optischen Achsen eines doppelbrechenden Kristalls sind nicht zu verwechseln mit der optischen Achse eines Systems von Linsen und Spiegeln.

Ordentlicher und außerordentlicher Strahl

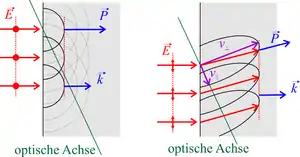
Konstruktion des ordentlichen (links) und des außerordentlichen (rechts) Strahles nach Huygens in einem einachsigen Kristall. Im linken Fall ist das Licht senkrecht zur Zeichenebene polarisiert, im rechten parallel dazu. Die Ausbreitungsgeschwindigkeiten sind relativ zur optischen Achse definiert, nicht relativ zur Polarisation.

Der ordentliche Strahl und der außerordentliche Strahl werden definiert durch die Orientierung ihres elektrischen Feldes zur Ebene, die durch die optische Achse und die Ausbreitungsrichtung des einfallenden Strahls aufgespannt wird (Hauptschnitt):

Der ordentliche Strahl ist der Anteil des einfallenden Strahls, dessen elektrisches Feld senkrecht zum Hauptschnitt steht. Für den ordentlichen Strahl gilt in einachsigen Kristallen das Snelliussche Brechungsgesetz für isotrope Medien,[1] d. h., er wird bei senkrechtem Einfall auf den doppelbrechenden Kristall nicht gebrochen. Die Elementarwellen des ordentlichen Strahls bilden Kugelwellen, die dem Huygensschen Prinzip genügen.[2]
Der zweite, der außerordentliche Strahl, hingegen ist der Anteil des einfallenden Strahls, dessen elektrisches Feld im Hauptschnitt des Kristalls schwingt. Für ihn gilt das Brechungsgesetz nicht, d. h., er wird auch bei senkrechtem Einfall auf den doppelbrechenden Kristall gebrochen. Die Elementarwellen des außerordentlichen Strahls bilden Rotationsellipsoide.

Die Wellenfronten für den ordentlichen und den außerordentlichen Strahl breiten sich mit unterschiedlichen Geschwindigkeiten $v_{\perp }$ und $v_{\|}$ aus, daraus folgen die zugehörigen Brechungsindizes:

n_{\mathrm {o} }={\frac {c}{v_{\perp }}}

und

n_{\mathrm {ao} }={\frac {c}{v_{\|}}}

mit der Lichtgeschwindigkeit c im Vakuum.

Die Differenz der Brechungsindizes ( $\Delta n=n_{\mathrm {ao} }-n_{o}$ ) ist ein Maß für die Doppelbrechung. Das Vorzeichen wird als optischer Charakter oder optische Orientierung bezeichnet. Für Kalkspat ist $\Delta n=-0{,}172$ . Kalkspat ist daher ein optisch negativer einachsiger Kristall, d. h., in ihm bewegt sich der außerordentliche Strahl schneller als der ordentliche:

${\begin{aligned}\Delta n&<0\\\Leftrightarrow n_{\mathrm {ao} }&<n_{\mathrm {o} }\\\Leftrightarrow {\frac {c}{v_{\|}}}&<{\frac {c}{v_{\perp }}}\\\Leftrightarrow v_{\|}&>v_{\perp }\end{aligned}}$

In diesem Zusammenhang spricht man auch von der schnellen und der langsamen Achse. In einem optisch negativen einachsigen Kristall verläuft die schnelle Achse parallel zur optischen Achse des Kristalls und die langsame Achse senkrecht zu ihr.

Entsprechend bewegt sich in einem optisch positiven einachsigen Kristall der außerordentliche Strahl langsamer als der ordentliche:

${\begin{aligned}\Delta n&>0\\\Leftrightarrow n_{\mathrm {ao} }&>n_{\mathrm {o} }\\\Leftrightarrow v_{\|}&<v_{\perp }\end{aligned}}$

Daher verläuft in einem optisch positiven einachsigen Kristall die schnelle Achse senkrecht zur optischen Achse des Kristalls, während die langsame Achse mit der optischen Achse übereinstimmt.

Zirkulare Doppelbrechung

dichroitische zirkulare Doppelbrechung bei Polystyrol-Platten zwischen gekreuzten Polarisationsfiltern, hervorgerufen durch Texturen bei der Formgebung

Die Eigenschaft optisch aktiver Substanzen, einen unterschiedlichen Brechungsindex für links- und rechts-zirkular polarisiertes Licht zu zeigen, wird als zirkulare Doppelbrechung bezeichnet.[3]

Sie wurde erstmals 1811 von Dominique François Jean Arago am Quarz beschrieben. Dort ist der Effekt ungefähr um den Faktor 100 geringer als die lineare Doppelbrechung. Da sich beide Effekte überlagern, kann die zirkulare Doppelbrechung nur dann beobachtet werden, wenn die lineare Doppelbrechung nicht auftritt. Bei Quarz ist dies entlang der optischen Achse der Fall.

Um die Drehung eines linear polarisierten Strahls durch die zirkulare Doppelbrechung in einem Material zu berechnen, kann dieser als eine kohärente Überlagerung eines links- und eines rechtsdrehenden Anteils mit gleicher Intensität beschrieben werden. Durch das Material bewegen sich die beiden Anteile mit unterschiedlichen Phasengeschwindigkeiten (die größere Phasengeschwindigkeit entspricht dem kleineren Brechungsindex). Nach dem Materialdurchgang ergibt die Überlagerung beider Anteile wieder einen linear polarisierten Strahl. Die Phasendifferenz Δφ der beiden Anteile nach dem Materialdurchgang zeigt sich in einer Drehung der Polarisations-Schwingungsebene um den Winkel Δφ/2 gegenüber der Schwingungsebene vor dem Materialdurchgang. Bei Quarz beträgt dieser Winkel ±21,7 °/mm Materialdicke (±, da Quarz sowohl rechts- als auch linksdrehend auftritt).

Eine Rechtsdrehung wird mit einem positiven Drehwinkel beschrieben und entsteht, wenn der Brechungsindex für den linksdrehenden Anteil größer ist als der für den rechtsdrehenden Anteil: $n_{\text{L}}>n_{\text{R}}$ .
Eine Linksdrehung wird mit einem negativen Drehwinkel beschrieben und entsteht, wenn der Brechungsindex für den rechtsdrehenden Anteil größer ist als der für den linksdrehenden Anteil: $n_{\text{R}}>n_{\text{L}}$ .

Die Ursache für die zirkulare Doppelbrechung beim Quarz ist sein „schraubenförmiger“ Kristallbau.[3] Aber nicht nur kristalline Materialien mit einer „schraubenförmigen“ Struktur zeigen ein Drehvermögen der Polarisationsebene, auch Flüssigkeiten weisen diese Eigenschaft auf, z. B. Terpentin. Die Ursache hierfür liegt ebenfalls in ihrem molekularen Aufbau, die Chiralität genannt wird. Weiterhin kann eine zirkulare Doppelbrechung durch ein Magnetfeld induziert werden, siehe Faraday-Effekt, z. B. bei Bleisilikatglas.

Vergleichbare Effekte gibt es auch für das Absorptionsverhalten von Materialien, siehe zirkularer Dichroismus.

Doppelbrechende Materialien

Eigenschaften

Die Tabellen enthalten die Brechungsindizes gängiger uni- bzw. biaxialer Systeme bei der Wellenlänge von orange-rotem Licht:

Uniaxiale Kristalle, für $\lambda$ =590 nm[4]
Material	n_o	n_ao	$\Delta$ n = n_ao - n_o
Beryll Be₃Al₂(SiO₃)₆	1,602	1,557	−0,045
Kalkspat CaCO₃	1,658	1,486	−0,172
Kalomel Hg₂Cl₂	1,973	2,656	+0,683
Eis H₂O	1,309	1,313	+0,014
Lithiumniobat LiNbO₃	2,272	2,187	−0,085
Magnesiumfluorid MgF₂	1,380	1,385	+0,006
Quarz SiO₂	1,544	1,553	+0,009
Rubin Al₂O₃	1,770	1,762	−0,008
Rutil TiO₂	2,616	2,903	+0,287
Saphir Al₂O₃	1,768	1,760	−0,008
Natriumnitrat NaNO₃	1,587	1,336	−0,251
Turmalin (komplexes Silikat)	1,669	1,638	−0,031
a-Zirkon ZrSiO₄	1,960	2,015	+0,055
b-Zirkon ZrSiO₄	1,920	1,967	+0,047

Biaxiale Kristalle, für $\lambda$ = 590 nm[4]
Material	n_a	n_β	n_ɣ
Borax	1,447	1,469	1,472
Bittersalz MgSO₄·7(H₂O)	1,433	1,455	1,461
Glimmer, Biotit	1,595	1,640	1,640
Glimmer, Muskovit	1,563	1,596	1,601
Olivin (Mg, Fe)₂SiO₄	1,640	1,660	1,680
Perovskit CaTiO₃	2,300	2,340	2,380
Topas	1,618	1,620	1,627
Ulexit	1,490	1,510	1,520

Anwendung

Doppelbrechende Materialien werden z. B. in Verzögerungsplatten und Polarisatoren verwendet. Zu den doppelbrechenden Polarisatoren zählen unter anderem das Nicolsche Prisma oder das Glan-Thompson-Prisma. Sie ermöglichen es, aus unpolarisiertem Licht linear polarisiertes Licht zu erzeugen.

Bei optischen Abbildungen können doppelbrechende Materialien als optischer Tiefpass eingesetzt werden, um beispielsweise den im Zusammenhang mit Bayer-Sensoren auftretenden Alias-Effekt zu vermindern.

Doppelbrechung kann auch als störender Effekt auftreten, z. B. beim Spritzprägen von Compact Discs.[5] Verursacht wird die Doppelbrechung hier durch mechanische Verspannungen innerhalb der Polycarbonat-Schicht, beispielsweise durch thermische Belastung oder Scherbeanspruchung des Materials.

Verschiedene Theorien besagen, dass die Doppelbrechung mit Sonnensteinen ein historisches Hilfsmittel war, um bei bedecktem Himmel den Sonnenstand zu bestimmen und Schiffe zu navigieren.

Nachweis

Doppelbrechende Proteinkristalle
unter einem Polarisationsmikroskop

Bei Drehung der Probe zwischen gekreuzten Polarisationsfiltern ändert sich die Helligkeit bzw. die Farbe des doppelbrechenden Objektes, während optisch isotrope Materialien keine Veränderungen im Bild zeigen.

Der Nachweis einer doppelbrechenden Substanz kann daher z. B. auch im Polarisationsmikroskop erfolgen.

Auch mithilfe der Immersionsmethode ist es möglich, doppelbrechende Materialien zu identifizieren.

Literatur

Werner Döring: Einführung in die Theoretische Physik, Band III (Optik). Sammlung Göschen, Berlin 1957.
Niedrig, Heinz., Eichler, Hans-Joachim., Bergmann, Ludwig., Schaefer, Clemens.: 9. Aufl. De Gruyter, Berlin 1993, ISBN 3-11-012973-6, S. 496 ff

Weblinks

Commons: Doppelbrechung – Album mit Bildern, Videos und Audiodateien

Skript mit einem Abschnitt über Polarisationsoptik (PDF, 680 KiB)
Virtuelles Polarisationsmikroskop

Einzelnachweise

Wolfgang Zinth, Ursula Zinth: Optik. Oldenbourg Wissenschaftsverlag, 2005, ISBN 978-3-486-27580-3, S. 230.
Hans-Joachim Bautsch, Will Kleber, Joachim Bohm: Einführung in die Kristallographie. Oldenbourg Wissenschaftsverlag, 1998, ISBN 978-3-486-27319-9, S. 273.
Wilhelm Raith, Clemens Schaefer: Elektromagnetismus. Walter de Gruyter, 1999, ISBN 978-3-11-016097-0, S. 425–426.
Glenn Elert: Refraction. In: The Physics Hypertextbook. Archiviert vom Original am 17. September 2009. Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 Abgerufen am 21. Dezember 2010.
R. Wimberger-Friedl: Analysis of the birefringence distributions in compact discs of polycarbonate. In: Polymer Engineering & Science. Band 30, Nr. 14, 1990, S. 813–820, doi:10.1002/pen.760301403.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Wolfgang Zinth, Ursula Zinth: Optik. Oldenbourg Wissenschaftsverlag, 2005, ISBN 978-3-486-27580-3, S. 230.

[2] Hans-Joachim Bautsch, Will Kleber, Joachim Bohm: Einführung in die Kristallographie. Oldenbourg Wissenschaftsverlag, 1998, ISBN 978-3-486-27319-9, S. 273.

[RaithSchaefer-3] Wilhelm Raith, Clemens Schaefer: Elektromagnetismus. Walter de Gruyter, 1999, ISBN 978-3-11-016097-0, S. 425–426.

[hypertextbook-4] Glenn Elert: Refraction. In: The Physics Hypertextbook. Archiviert vom Original am 17. September 2009. Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 Abgerufen am 21. Dezember 2010.

[5] R. Wimberger-Friedl: Analysis of the birefringence distributions in compact discs of polycarbonate. In: Polymer Engineering & Science. Band 30, Nr. 14, 1990, S. 813–820, doi:10.1002/pen.760301403.