Mößbauer-Effekt

Unter dem Mößbauer-Effekt (nach dem Entdecker Rudolf Mößbauer, auch Mössbauer-Effekt geschrieben) versteht man die rückstoßfreie Kernresonanzabsorption von Gammastrahlung durch Atomkerne. Kombiniert man Emission der Gammaquanten und ihre erneute Absorption, erhält man mit der Mößbauerspektroskopie eine extrem empfindliche Messmethode für die Energieänderung der Gammaquanten. Dazu muss sich der Atomkern in einem Kristallgitter befinden, das den Rückstoß übernehmen kann und durch seine große Masse dem Gammaquant kaum Energie entzieht (siehe auch elastischer Stoß). Rudolf Mößbauer erhielt für seine Entdeckung 1961 den Nobelpreis für Physik.

Eigenschaften der Gammastrahlung

Seit Beginn des 20. Jahrhunderts kennen Physiker die Gammastrahlung als eine Erscheinung der Radioaktivität. Als Entdecker gelten Antoine Henri Becquerel und Paul Villard, wobei letzterer um 1900 nachweisen konnte, dass es sich bei der Gammastrahlung um extrem energiereiche elektromagnetische Wellen handelt. Gammastrahlung entsteht u. a. infolge eines vorausgehenden Alpha- oder Betazerfalls, da sich der Atomkern nach diesem Zerfall in einem angeregten Zustand befindet.

Die Emission des Gamma-Quants verändert dabei den Kern im Gegensatz zu einem α- oder β-Zerfall materiell nicht, es findet keine Umwandlung in ein anderes Nuklid statt. Lediglich die im Kern gespeicherte Anregungsenergie wird als ein oder mehrere Strahlungsquanten abgegeben, genau wie auch angeregte Elektronen ihre Energie in Form von Lichtquanten abgeben. Atomkerne können Gamma-Quanten auch absorbieren, wodurch sie in einen – relativ zum vorherigen Zustand gesehen – angeregten Zustand übergehen.

Aus theoretischen Überlegungen folgerte man früh, dass die von den meisten Kernen emittierte Gammastrahlung durch sehr scharfe Energieniveaus gekennzeichnet ist und somit eine extrem geringe Linienbreite haben muss. Man kann Atomkerne auch mit einem Schwingquarz vergleichen, der nur mit einer bestimmten Frequenz angeregt werden kann. Tatsächlich ist die Energiekonstanz (und damit die Frequenzgenauigkeit) vieler Gamma-Strahlungsübergänge vergleichbar mit der Genauigkeit von Atomuhren.

Die Ausgangssituation vor Mößbauer

Die theoretisch vorausgesagte spektrale Reinheit der Gamma-Strahlung war vor der von Mößbauer gemachten Entdeckung praktisch nicht nachweisbar. Aufgrund der hohen Energie der Gamma-Quanten kann man deren Frequenz nur recht grob durch kalorimetrische Methoden bestimmen. Ein elektronischer Frequenzzähler funktioniert im Frequenzbereich der Gamma-Strahlung nicht mehr.

Darüber hinaus erfährt der Kern beim Aussenden eines Gamma-Quants einen nicht zu vernachlässigenden Rückstoß. Dies liegt an der hohen Energie der Quanten, die als Photonen zwar keine Masse, jedoch einen Impuls besitzen. Der auf den Kern wirkende Rückstoß bewirkt eine Verringerung der Energie des Gamma-Quants: Verliert der Kern mit der Masse $M$ durch die Emission des Photons die Energie $E_{0}$ , so erfährt er wegen Energie- und Impulserhaltung einen Rückstoß der Energie $E_{R}$ . Das abgestrahlte Photon besitzt dann die um $\Delta E$ verringerte Energie $E_{\gamma }=E_{0}-\Delta E$ .

E_{R}=\Delta E={\frac {E_{\mathrm {\gamma } }^{2}}{2Mc^{2}}}

Das ergibt sich aus $E_{R}={\tfrac {({\vec {p}})^{2}}{2M}}$ (mit der Kernmasse $M$ ) und der relativistischen Energie-Impuls-Beziehung für das Photon $E_{\mathrm {\gamma } }=pc=|{\vec {p}}|\,c$ .

Gleichwertig zu dieser Beschreibung ist eine Betrachtung aus der Sicht des sich nun bewegenden Kerns unter Berücksichtigung der Doppler-Frequenzverschiebung. Soll nun ein Kern das von einem anderen Kern emittierte Gamma-Quant wieder absorbieren, so ist dies eigentlich nur dann möglich, wenn zuvor beide Kerne genau mit der doppelten Rückstoßgeschwindigkeit aufeinander zugeflogen sind (doppelt, weil auch bei der Absorption ein gleich starker Rückstoß erfolgt). Die erforderliche Geschwindigkeit kann experimentell zum Beispiel dadurch erzeugt werden, dass man Quelle oder Absorber auf den Rand einer schnell rotierenden Zentrifuge oder eines Drehtellers setzt oder die Quelle erhitzt, um die thermische Linienverbreiterung zu erhöhen. Mößbauer verfolgte beide Methoden. Die Verwendung einer Zentrifuge oder eines Drehtellers (wie sie zuerst P. B. Moon 1951 für die Kernresonanzfluoreszenz verwendete[1]) war aber bei der von ihm verwendeten Iridium-Quelle nicht realisierbar, da sie ohne den später von ihm entdeckten Effekt Überschallgeschwindigkeit erfordert hätte.

Mößbauers Experiment

Mößbauer wollte im Rahmen seiner Dissertation, die 1958 an der TU München bei Heinz Maier-Leibnitz erfolgte und für die er zuvor am Max-Planck-Institut für medizinische Forschung in Heidelberg experimentierte, die Wahrscheinlichkeit für eine solche Emission und anschließende Absorption eines Gamma-Quants ermitteln. Die Voraussetzung, dass die beiden beteiligten Kerne sich mit der richtigen Geschwindigkeit aufeinander zubewegen, sollte durch die Wärmebewegung der Atome erfüllt werden.

Hier der schematische Versuchsaufbau seines Experimentes:

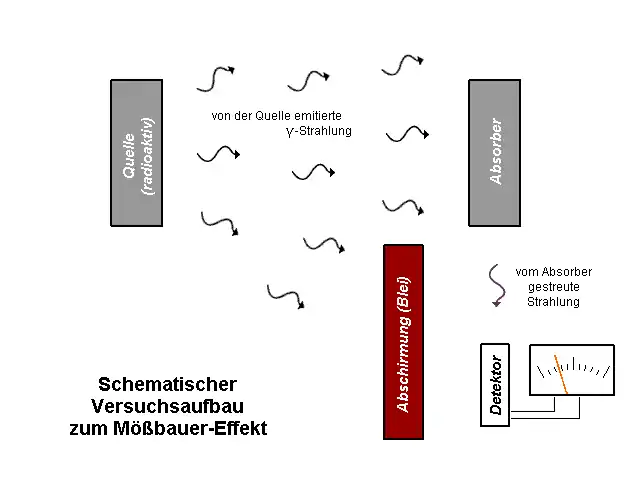
Auf der linken Seite befindet sich eine radioaktive Quelle für Gamma-Strahlen. Einige der Strahlen treffen rechts auf einen Absorber, der die gleichen Atome wie die Quelle enthält, diese sind jedoch von sich aus nicht radioaktiv. Wird nun ein Kern im Absorber von einem Gamma-Photon getroffen, so kann, falls oben genannte Voraussetzung erfüllt ist, das Gamma-Photon zum Detektor hin gestreut werden. Der direkte Weg der Strahlung zum Detektor wird durch eine Abschirmung aus Blei blockiert.

Die Temperatur von Festkörpern, Flüssigkeiten und Gasen ist korreliert mit der Geschwindigkeit der Teilchen (Atome, Moleküle) in denselben. Je höher die Temperatur, desto schneller bewegen sich die Teilchen im Mittel. Allerdings ist die Geschwindigkeit aller Teilchen nicht gleich, sondern statistisch verteilt, ebenso wie die Bewegungsrichtungen der Teilchen.

Mößbauer erwartete, dass mit steigender Temperatur die Wahrscheinlichkeit für eine Emission und anschließende Absorption eines Gamma-Quants ansteigen sollte, da sich statistisch gesehen mehr Atome mit der richtigen Geschwindigkeit aufeinander zubewegen. Umgekehrt sollte sich bei sehr niedrigen Temperaturen die Wahrscheinlichkeit für diesen Vorgang nahezu auf Null verringern, da die Atome im Mittel so langsam sind, dass die erforderliche Geschwindigkeitsdifferenz kaum einmal erreicht wird.

Das zunächst überraschende Ergebnis

Die ersten Messungen nahe der Zimmertemperatur und darüber schienen Mößbauers Erwartungen zunächst zu bestätigen. Als er jedoch aus Neugier begann, Quelle und Absorber abzukühlen, stellte er überraschend fest, dass die Wahrscheinlichkeiten für die Gammaemission und -absorption bei tiefen Temperaturen plötzlich wieder steil anstiegen und zwar über das Maß hinaus, welches bei höheren Temperaturen gemessen worden war.

Mößbauer führte seine Experimente an Festkörpern durch. In diesen schwingen die Atome um ihre Ruhepositionen im Kristallgitter (bei steigender Temperatur mit zunehmender Amplitude). Jedoch sind aufgrund der Quantenmechanik nicht alle Schwingungszustände erlaubt, sondern nur diskrete Energiezustände (Phononen). Aus diesem Grund kann der Kern bei der Emission und Absorption eines Gamma-Quants keinen beliebig starken Impuls in Form von Schwingungsenergie abgeben. Da die Aufnahme und Abgabe der Schwingungsenergie gequantelt ist, besteht eine bestimmte Wahrscheinlichkeit (gegeben durch den sog. Debye-Waller-Faktor), dass das Atom keine Schwingungsenergie erzeugt und seinen Rückstoßimpuls an das gesamte Kristallgitter[2] übertragen kann. Da dessen Masse die des Kerns wesentlich übersteigt, erfolgen Gamma-Emission und Absorption in diesem Fall nahezu rückstoßfrei.

Mößbauer überprüfte daraufhin das Ergebnis genauer, indem er die Quelle auf einem Drehteller befestigte und so über den Dopplereffekt die Energie variieren und die Resonanz vermessen konnte.

Bei dem von Mößbauer verwendeten Isotop Iridium-191 war die Gammastrahlenenergie 129 keV und die natürliche Linienbreite in der Größenordnung von $10^{-5}$ eV. Die Energieauflösung betrug damit vorher nie erreichte $10^{-10}$ . Bald darauf wurden weitere Mößbauerlinien entdeckt, insbesondere Fe-57 mit rückstoßfreier Emission bei Zimmertemperatur, einer Gammastrahlenenergie von 14,4 keV und einer natürlichen Linienbreite von $\approx 5\cdot 10^{-9}$ eV[3].

Anwendungen

Durch die rückstoßfreie Kernresonanzabsorption ergeben sich völlig neuartige Messverfahren auf den Gebieten der Festkörperphysik, Materialforschung und Chemie. Des Weiteren können auch Vorhersagen der allgemeinen Relativitätstheorie mit diesem Effekt untersucht werden. So wurde 1960 in einem Mößbauer-Experiment von Robert Pound und Glen Rebka festgestellt, dass, wenn sich Quelle und Absorber in rund 20 Metern Abstand senkrecht voneinander entfernt befinden, das Gravitationspotential der Erde zu einer messbaren Energieänderung der Lichtquanten beim Durchlaufen des Höhenunterschiedes führt (Pound-Rebka-Experiment).

Die vielfältigsten Anwendungen findet der Mößbauer-Effekt heute in der Chemie. Da die Ausprägung der Elektronenhülle eines Moleküls geringfügig auf die Energieniveaus der Anregungszustände seiner Atomkerne zurückwirkt, hat sich der Mößbauer-Effekt zu einem unersetzlichen Instrument in der chemischen Analyse entwickelt (siehe hierzu: Mößbauerspektroskopie).

Literatur

Rudolf Mößbauer: Gammastrahlung in Ir191. In: Zeitschrift für Physik. Band 151, 1958, S. 124–143, doi:10.1007/BF01344210.
Rudolf Mößbauer: Recoilless Nuclear Resonance Absorption of Gamma Radiation, Nobel Lecture 1961, Online
Hans Frauenfelder: The Mössbauer Effect, W. A. Benjamin, New York, 1962
Leonard Eyges: Physics of the Mössbauer Effect. In: American Journal of Physics. Band 33, 1965, S. 790–802, doi:10.1119/1.1970986.
Philipp Gütlich: Physikalische Methoden in der Chemie: Mößbauer-Spektroskopie I. In: Chemie in unserer Zeit. Band 4, 1970, S. 133–144, doi:10.1002/ciuz.19700040502.
Horst Wegener: Der Mössbauer-Effekt und seine Anwendung in Physik und Chemie, BI Wissenschaftsverlag 1965

Weblinks

Mößbauer-Effekt (LEIFI)

Anmerkungen

P. B. Moon: Resonant Nuclear Scattering of Gamma-Rays: Theory and Preliminary Experiments. In: Proceedings of the Physical Society. Section A. Band 64, Nr. 1, Januar 1951, S. 76–82, doi:10.1088/0370-1298/64/1/311 (Zitiert im Nobelvortrag von Mößbauer).
Der Bereich des Kristallgitters, der Rückstoßenergie aufnehmen kann, ergibt sich grob aus dem Volumen der Kugel, deren Radius der Entfernung entspricht, die der Schall in diesem Gitter während der mittleren Lebensdauer des Gamma-Übergangs zurücklegen kann.
Hans Kuzmany: Solid-State Spectroscopy: An Introduction. Springer Science & Business Media, 1998, S. 300 (eingeschränkte Vorschau in der Google-Buchsuche).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] P. B. Moon: Resonant Nuclear Scattering of Gamma-Rays: Theory and Preliminary Experiments. In: Proceedings of the Physical Society. Section A. Band 64, Nr. 1, Januar 1951, S. 76–82, doi:10.1088/0370-1298/64/1/311 (Zitiert im Nobelvortrag von Mößbauer).

[2] Der Bereich des Kristallgitters, der Rückstoßenergie aufnehmen kann, ergibt sich grob aus dem Volumen der Kugel, deren Radius der Entfernung entspricht, die der Schall in diesem Gitter während der mittleren Lebensdauer des Gamma-Übergangs zurücklegen kann.

[3] Hans Kuzmany: Solid-State Spectroscopy: An Introduction. Springer Science & Business Media, 1998, S. 300 (eingeschränkte Vorschau in der Google-Buchsuche).