Elektromagnetische Induktion

Unter elektromagnetischer Induktion (auch Faradaysche Induktion, nach Michael Faraday, kurz Induktion) versteht man das Entstehen eines elektrischen Feldes bei einer Änderung des magnetischen Flusses.

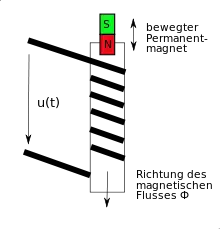
Ein bewegter Permanentmagnet erzeugt an den Klemmen einer Spule eine elektrische Spannung U(t).

In vielen Fällen lässt sich das elektrische Feld durch Messung einer elektrischen Spannung mit einer Spule direkt nachweisen. Ein typisches Beispiel hierfür zeigt das nebenstehende Bild: Durch die Bewegung des Magneten wird eine elektrische Spannung induziert, die an den Klemmen der Spule messbar ist und für weitere Anwendungen bereitsteht.

Die elektromagnetische Induktion wurde 1831 von Michael Faraday bei dem Bemühen entdeckt, die Funktionsweise eines Elektromagneten (Strom erzeugt Magnetfeld) umzukehren (Magnetfeld erzeugt Strom). Der Zusammenhang ist eine der vier Maxwellschen Gleichungen. Die Induktionswirkung wird technisch vor allem bei elektrischen Maschinen wie Generatoren, Elektromotoren und Transformatoren genutzt. Bei diesen Anwendungen treten stets Wechselspannungen auf.

Geschichtliche Entwicklung

Prinzip von Faradays historischem Experimentalaufbau: Eine Änderung des magnetischen Flusses in der linken Spule induziert eine Spannung in der rechten Spule.[1]

Michael Faraday – Entdecker der Induktion

Die elektromagnetische Induktion als Teil der Maxwellschen Gleichungen und der klassischen Elektrodynamik spiegelt den Kenntnisstand zum Ende des 19. Jahrhunderts wider. Zum damaligen Zeitpunkt wurden teilweise andere Begriffe und Formelzeichen benutzt, die grundlegenden Vorstellungen über den Induktionsvorgang wurden jedoch zu dieser Zeit geschaffen.

Als Entdecker des Induktionsgesetzes gelten Michael Faraday, Joseph Henry und Hans Christian Ørsted, die das Induktionsgesetz im Jahr 1831 unabhängig voneinander formulierten, wobei Faraday seine Ergebnisse als Erster veröffentlichte.[2][3]

In Faradays erstem Demonstrationsaufbau zur Induktion vom 29. August 1831[4] wickelte er zwei Leiterdrähte auf die gegenüberliegenden Seiten eines Eisenkerns; eine Anordnung, die modernen Ringkerntransformatoren ähnelt. Er erwartete aufgrund seiner Kenntnisse über Permanentmagnete, dass sich – sobald in einer der beiden Leitungen ein Strom zu fließen beginnt – eine Welle entlang des Rings ausbreitet und zu einem Stromfluss in der Leitung auf der anderen Seite des Rings führt. Im Experiment schloss er an einer der beiden Leitungen ein Galvanometer an und beobachtete jedes Mal einen kurzen Zeigerausschlag, wenn er den anderen Draht an eine Batterie anschloss.[5] Die Ursache dieser Induktionserscheinung war die Änderung des magnetischen Flusses in der von der Leiterschleife aufgespannten Fläche. In der folgenden Zeit identifizierte Faraday weitere Beispiele elektromagnetischer Induktion. So beobachtete er Ströme wechselnder Richtung, wenn er einen Permanentmagneten rasch in eine Spule hinein und wieder heraus bewegte. Aus den historischen Untersuchungen ging auch die sogenannte Faradayscheibe, ein Gleichstromgenerator, hervor,[6] die aus heutiger Sicht als sogenannte Bewegungsinduktion beschrieben wird und ihre Ursache in der Bewegung des Leiters und der mitgeführten Ladungen im magnetischen Feld hat. Faraday veröffentlichte das Gesetz, beginnend mit “The relation which holds between the magnetic pole, the moving wire or metal, and the direction of the current evolved, i. e. the law which governs the evolution of electricity by magneto-electric induction, is very simple, although rather difficult to express.” (deutsch: „Die Beziehung, die zwischen dem magnetischen Pol, dem sich bewegenden Draht oder Metall und der Richtung des fließenden Stroms besteht, d. h., das Gesetz, das die Entstehung der Elektrizität durch magnetisch-elektrische Induktion beherrscht, ist sehr einfach, jedoch ziemlich schwer auszudrücken.“)[7]

Bedeutende Beiträge stammten auch von Emil Lenz (Lenzsche Regel), Franz Ernst Neumann und Riccardo Felici.

Anfang des 20. Jahrhunderts erfolgte die relativistische Eingliederung des Induktionsgesetzes im Rahmen der speziellen Relativitätstheorie. Anders als in der Mechanik, bei der sich die spezielle Relativitätstheorie erst bei Geschwindigkeiten nahe der Lichtgeschwindigkeit merklich auswirkt, sind relativistische Effekte in der Elektrodynamik schon bei sehr kleinen Geschwindigkeiten zu beobachten. So konnte im Rahmen der Relativitätstheorie beschrieben werden, wie sich beispielsweise die Beträge der elektrischen und magnetischen Feldkomponenten in Abhängigkeit von der Bewegung zwischen einem Beobachter und einer beobachteten elektrischen Ladung verändern. Diese Abhängigkeiten in der relativen Bewegung zueinander zwischen verschiedenen Bezugssystemen werden durch die Lorentz-Transformation beschrieben. Dabei zeigt sich, dass das Induktionsgesetz in Kombination mit den restlichen Maxwellschen Gleichungen „lorentzinvariant“ ist. Das heißt, die Struktur der Gleichungen wird durch die Lorentztransformation zwischen verschiedenen Bezugssystemen nicht verändert. Dabei wird deutlich, dass die elektrischen und magnetischen Felder nur zwei Erscheinungsformen desselben Phänomens sind.

Allgemeines

Bei der durch Induktion infolge einer magnetischen Flussdichteänderung entstehenden elektrischen Spannung handelt es sich um eine sogenannte Umlaufspannung. Eine solche Umlaufspannung tritt nur in Feldern mit einem sogenannten Wirbelanteil auf, d. h. in Feldern, bei denen Feldlinien nicht an einem bestimmten Punkt im Raum enden, sondern sich beispielsweise im Kreis drehen oder „im Unendlichen“ verschwinden. Hierdurch unterscheidet sich die Induktionsspannung von Spannungen, wie sie beispielsweise bei einer Batterie vorkommen (Potentialfeld). Die Feldlinien der sog. Urspannungsquellen EMK einer Batterie (siehe elektromotorische Kräfte)[8] verlaufen stets von positiven zu negativen Ladungen und sind daher niemals geschlossen.

In mathematischer Form lässt sich das Induktionsgesetz durch jede der folgenden drei Gleichungen beschreiben:

**Induktionsgesetz in SI-Einheiten**
Differentielle Form	Integralform I	Integralform II
$\operatorname {rot} {\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}$	$\,\,\oint \limits _{\partial {\mathcal {\mathcal {A}}}(t)}{{\vec {E}}\cdot {\text{d}}{\vec {s}}}=-\int \limits _{{\mathcal {A}}(t)}{{\frac {\partial {\vec {B}}}{\partial t}}\cdot {\text{d}}{\vec {A}}}$	$\,\,\oint \limits _{\partial {\mathcal {A}}(t)}{({\vec {E}}+{\vec {u}}\times {\vec {B}}(t))\cdot {\text{d}}{\vec {s}}}=-{\frac {\text{d}}{{\text{d}}t}}\int \limits _{{\mathcal {A}}(t)}{\vec {B}}(t)\cdot {\text{d}}{\vec {A}}$

In den Gleichungen steht ${\vec {E}}$ für die elektrische Feldstärke und ${\vec {B}}$ für die magnetische Flussdichte. Die Größe ${\text{d}}{\vec {A}}$ ist das orientierte Flächenelement und $\partial {\mathcal {A}}$ der Rand (die Konturlinie) der betrachteten Integrationsfläche ${\mathcal {A}}$ ; ${\vec {u}}$ ist die lokale Geschwindigkeit der Konturlinie in Bezug auf das zugrundeliegende Bezugssystem. Das auftretende Linienintegral führt entlang einer geschlossenen Linie $\partial {\mathcal {A}}$ und endet daher am Startpunkt. Ein Multiplikationspunkt zwischen zwei Vektoren markiert deren Skalarprodukt.

Alle Größen müssen sich auf dasselbe Bezugssystem beziehen.

Grundlegende Experimente

Transformatorprinzip: Das von der linken Wicklung verursachte, sich verändernde Magnetfeld bewirkt in der rechten Wicklung eine elektrische Spannung.[1]

Im Folgenden werden mehrere beliebte Experimente zur Demonstration der elektromagnetischen Induktion beschrieben.

Ein grundlegendes Induktionsexperiment wird schon im Einleitungstext aufgegriffen. Bewegt man den im Einleitungstext dargestellten Permanentmagneten in der Spule auf und ab, so lässt sich an den Klemmen der Spule mit dem Oszilloskop eine elektrische Spannung abgreifen.

Dieses Prinzip wird beim Transformator genutzt, dessen Funktionsprinzip im nebenstehenden Bild skizziert wird: Schließt man den Batteriestromkreis in der linken Wicklung (Primärwicklung), so entstehen kurzzeitig im Eisenkern ein sich veränderndes magnetisches Feld und in der rechten Wicklung (Sekundärwicklung) eine elektrische Spannung, die beispielsweise mithilfe eines Voltmeters oder einer Glühlampe nachgewiesen werden kann. Öffnet man den Batteriestromkreis auf der linken Seite wieder, entsteht in der rechten Wicklung erneut eine elektrische Spannung. Diese hat jedoch ein umgekehrtes Vorzeichen.

Induktive Erwärmung

Sofern der Eisenkern elektrisch leitfähig ist, können schon im Kern elektrische Ströme induziert werden, die den Eisenkern erhitzen (siehe Bild „Erhitzung einer Metallstange“). Dies versucht man bei Transformatoren zu vermeiden, indem man geblechte Kerne verwendet, die dem Strom einen höheren Widerstand entgegensetzen.

Die Erzeugung einer elektrischen Spannung lässt sich auch durch Bewegung der Leiter erzeugen. So lässt sich an den Klemmen einer Leiterschleife oder einer Spule eine elektrische Wechselspannung abgreifen, wenn man die Leiterschleife in einem zeitlich konstanten Magnetfeld dreht, wie im Abschnitt Leiterschleife im Magnetfeld gezeigt. Nach dem dort gezeigten Prinzip (aber einer grundlegend verbesserten Anordnung) funktionieren die in Kraftwerken eingesetzten Generatoren zur Bereitstellung elektrischer Energie im Stromversorgungsnetz. In dem gezeigten Experiment kann die Wirkungsrichtung grundsätzlich umgedreht werden: Legt man an die Klemmen der drehbar gelagerten Leiterschleife eine elektrische Wechselspannung, so dreht sich die Leiterschleife um ihre Achse im magnetischen Feld (Synchronmotor).

Die Bewegung eines Leiters im Magnetfeld kann auch genutzt werden, um eine elektrische Gleichspannung zu erzeugen. Dies ist beispielhaft im Abschnitt Induktion durch Bewegung des Leiters gezeigt. Bewegt man den Leiterstab entlang der Schienen, die durch einen Schleifkontakt oder durch Räder elektrisch mit dem Leiterstab verbunden sind, so lässt sich am Voltmeter eine Gleichspannung messen, die von der Geschwindigkeit des Leiterstabes, der magnetischen Flussdichte und dem Abstand der Schienen abhängt.

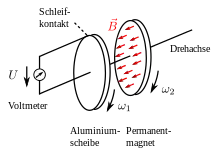
Faradayscheibe: Bei Drehung der Aluminiumscheibe lässt sich am Voltmeter infolge der Unipolarinduktion eine Gleichspannung abgreifen. Dreht man hingegen nur den Magneten, bleibt die Spannungsanzeige bei null. Dreht man gleichermaßen den Magneten und die Aluminiumscheibe, ist wiederum eine Spannung messbar.

Anstelle einer Linearbewegung lässt sich das Experiment auch mit einer Drehbewegung demonstrieren, wie am Beispiel der Faradayscheibe (Bild rechts) gezeigt. Im dargestellten Experiment übernimmt die Aluminiumscheibe die Funktion des bewegten Leiterstabes aus dem Experiment mit dem bewegten Leiterstab im Magnetfeld.

Dreht man die Aluminiumscheibe im magnetischen Feld, so lässt sich zwischen Schleifkontakt am äußeren Rand der Aluminiumscheibe und der Drehachse eine elektrische Spannung nachweisen, mit der sich beispielsweise auch eine Glühlampe betreiben lässt. Die Spannung an den Klemmen hängt dabei von der Stärke der magnetischen Flussdichte, der Drehgeschwindigkeit $\omega _{1}$ und dem Durchmesser der Scheibe ab.

Zum großen Erstaunen Faradays weist ein solcher Unipolargenerator jedoch unerwartete Eigenschaften auf, die in der Literatur noch lange nach Faradays Entdeckung diskutiert wurden und zu einer lange anhaltenden Kontroverse um die Frage führte, ob man dem Magnetfeld gleichsam wie einem materiellen Objekt eine Geschwindigkeit zuordnen könne und konkret, ob sich das Magnetfeld mit dem Magneten mitdreht.[9] Die wesentliche Entdeckung war, dass die Spannung entgegen einer naheliegenden intuitiven Annahme nachweislich nicht von der Relativbewegung zwischen dem Permanentmagneten und der Aluminiumscheibe abhängt. Denn dreht man im dargestellten Experiment beispielsweise nur den Permanentmagneten und lässt die Aluminiumscheibe ruhen ( $\omega _{1}=0,\,\omega _{2}\neq 0$ ), so ist trotz der vorhandenen Relativbewegung zwischen Magnet und Leiter keine Spannung zu beobachten. Dreht man hingegen beide Scheiben mit der gleichen Geschwindigkeit ( $\omega _{1}=\omega _{2}\neq 0$ ), so zeigt sich eine Spannung an, obwohl die beiden Scheiben sich relativ zueinander nicht bewegen. Ebenso ist eine Spannungsanzeige zu beobachten, wenn man die Spannung anstelle an der Aluminiumscheibe direkt an dem als elektrisch leitfähig angenommenen Permanentmagneten abgreift.

Das Prinzip ist ebenfalls umkehrbar und lässt stromdurchflossene Magnetscheiben kreiseln,[10][11] siehe Homopolarmotor.

Obwohl die Kontroverse um diese Frage im Rahmen der speziellen Relativitätstheorie Einsteins aufgeklärt werden kann[12] und es erwiesenermaßen nicht auf die Relativgeschwindigkeit zwischen Magnet und Leiter ankommt, wird im schulischen Unterricht auch heute teilweise noch das sogenannte Igelmodell des Magnetfeldes verwendet, dem zufolge die magnetischen Feldlinien wie Igelstacheln an dem Magneten befestigt seien. Induktion trete dem Modell entsprechend immer dann ein, wenn der Leiter die Feldlinien „schneide“ (Relativbewegung zwischen Leiter und Magnetfeld). Im Rahmen der Seminarlehrertagung „Physik“ in Dillingen 2002 wies Hübel[13] ausdrücklich auf die mit dem Igelmodell verbundenen Schwierigkeiten hin und betonte, das Igelmodell solle nicht als kausale Erklärung der Induktion missverstanden werden; es sei vielmehr nicht haltbar und könne zu falschen Vorstellungen führen.

Induktion Leiterschleife

Eine ähnlich häufige Fehlvorstellung wie das Igelstachelmodell betrifft die Annahme, induktive Vorgänge ließen sich mit der Kirchhoff'schen Maschengleichung erklären. Diese besagt, dass die Summe aller Spannungen in einem Stromkreis "einmal im Kreis herum" immer null ergibt. Aus dem Induktionsgesetz lässt sich für ruhende Stromkreise hingegen folgern, dass die Summe aller Spannungen "einmal im Kreis herum" der Änderung des magnetischen Flusses entspricht, die in der vom Stromkreis aufgespannten Fläche auftritt.

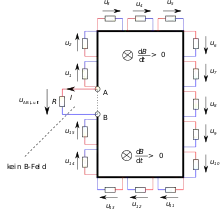
Das nebenstehende Bild zeigt zur Verdeutlichung eine Leiterschleife bestehend aus einem guten Leiter (schwarze Linie) und einem Widerstand R, der zur Messung der Spannung zwischen den Klemmen A und B genutzt wird. Im Bereich innerhalb des Rechtecks (bestehend aus dem Leiter und der gestrichelten Verbindung zwischen den Punkten A und B) existiert ein Magnetfeld, dessen zeitliche Ableitung ${\frac {\partial {\vec {B}}}{\partial t}}$ eine Zeitlang homogen und zeitlich konstant ist.

Misst man die Spannung zwischen den Klemmen A und B entlang einer Strecke durch die Luft, so ergibt sich ein von Null verschiedener Wert, der von der Flussänderung der umschlossenen Fläche abhängt: $u_{\mathrm {AB,Luft} }\neq 0$

Misst man die Spannung zwischen den Klemmen A und B hingegen entlang einer Strecke durch den Draht, so ergibt sich der Wert null: $u_{\mathrm {AB,Draht} }=u_{1}+u_{2}+\dotsb +u_{15}=0$ , da im Draht aufgrund des geringen Stromflusses und der guten Leitfähigkeit ein verschwindendes E-Feld herrscht und somit gilt: $u_{1}=u_{2}=\dotsb =u_{15}=0$

Der Begriff der „Spannung zwischen zwei Punkten“ ist bei Induktion nicht mehr eindeutig und muss durch die Angabe des Weges ergänzt werden (vgl. Wirbelfeld).

Induktion bei einer Leiterschleife

Allgemeine Formulierung des Induktionsgesetzes für eine Leiterschleife

Die zeitliche Änderung des durch eine Leiterschleife eingeschlossenen magnetischen Flusses ist an den Enden der Leiterschleife als Spannung messbar.

Obwohl die allgemeine Formulierung des Induktionsgesetzes keine Leiterschleife erfordert, soll zunächst wie in vielen einführenden Lehrbüchern üblich die Induktion an einer aus dünnem, gut leitfähigem Draht bestehenden Leiterschleife betrachtet werden. Hierdurch lassen sich eine große Anzahl technischer Anwendungen wie beispielsweise Motoren und Generatoren für Dreh- und Wechselstrom beschreiben und verstehen, ohne dass dazu eine Behandlung der relativistischen Aspekte der Feldtheorie oder die Anwendung der Lorentztransformation erforderlich wäre.

Für die zwischen beiden Drahtenden mit einem im Laborsystem ruhenden oder auch bewegten Messgerät (beispielsweise mit einem Oszilloskop) messbare elektrische Spannung $U$ ergibt sich unter den Voraussetzungen, die im nebenstehenden Bild gekennzeichnet sind:

U=+{\frac {{\text{d}}\Phi }{{\text{d}}t}}.

Hierbei ist $\Phi$ der magnetische Fluss

\Phi =\int \limits _{{\mathcal {A}}(t)}{\vec {B}}\cdot {\text{d}}{\vec {A}},

der durch eine (beliebige) von der Leiterschleife, den Zuleitungen zum Messgerät und den Leitungen im Messgerät begrenzte Fläche ${\mathcal {A}}(t)$ hindurchtritt. Es kann gezeigt werden, dass es bei der Berechnung des Flusses nicht auf die Form der Fläche, sondern ausschließlich auf deren Berandung ankommt. Ebenso ist es bei der Rechnung nicht notwendig zu unterscheiden, ob die elektrische Spannung der Anordnung durch eine Änderung der Flussdichte oder durch eine Bewegung des Leiters erzeugt wird.

Bei der Festlegung des Vorzeichens in der Gleichung $U={\tfrac {{\text{d}}\Phi }{{\text{d}}t}}$ ist zu beachten, dass das Vorzeichen sowohl von der Einbaurichtung des Messgerätes, als auch von der Flächenorientierung abhängt[14] und daher immer zusammen mit dem zugehörigen Schaltbild gelesen werden muss.

Die Flächenorientierung ist im Schaltbild durch den eingezeichneten Pfeil beim Flächenelement ${\text{d}}{\vec {A}}$ gekennzeichnet. Der Pfeil bei der Spannungsangabe $U$ definiert wiederum die Einbaurichtung des Messgerätes. Die vorliegende Bepfeilung bei der Spannung (Pfeil zeigt von oben nach unten) bedeutet, dass an der oberen Anschlussklemme das rote Anschlusskabel des Digitalvoltmeters[15] und an der unteren Anschlussklemme das schwarze Anschlusskabel des Digitalvoltmeters[16] angeschlossen wird. Würde man das Messgerät herumdrehen (Spannungspfeil von unten nach oben) oder die Flächenorientierung umgekehrt wählen, so würde sich in der Gleichung ein negatives Vorzeichen ergeben. Ein positives Vorzeichen ergäbe sich hingegen wiederum, wenn man sowohl die Orientierung des Spannungspfeils als auch die Flächenorientierung herumdrehen würde.

Beispiel: Induktion durch Bewegung des Leiters

Wird der Leiterstab bewegt, zeigt das Messgerät die Spannung

\textstyle U=vLB_{0}

an. Aus Sicht eines im Laborsystem ruhenden Beobachters ergibt sich im bewegten Leiterstab eine von null verschiedene elektrische Feldstärke. Das Feldlinienbild zeigt ein reines Quellenfeld, d. h. ein elektrostatisches Feld. Die beiden Schienen laden sich wie ein Kondensator gegeneinander auf. Die Wirbelstärke des E-Feldes ist überall gleich null.

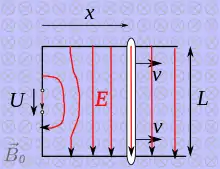
Der im nebenstehenden Bild skizzierte Messaufbau besteht aus einer ruhenden elektrisch leitfähigen Schienenanordnung, über die mit der Geschwindigkeit $v$ ein Leiterstab gleitet. Die Anordnung befindet sich in einem örtlich und zeitlich konstanten magnetischen Feld mit der Flussdichte ${\vec {B}}_{0}$ , das durch einen ruhenden Permanentmagneten oder eine ruhende mit Gleichstrom betriebene Spulenanordnung hervorgerufen wird. Die Spannung zwischen den beiden Schienen wird mit einem Voltmeter gemessen.

Die Spannung $U$ hängt von der Stärke der magnetischen Flussdichte $B$ , der Geschwindigkeit $v$ und dem Schienenabstand $L$ ab:

U=L\cdot B_{0}\cdot v

Diese Spannung kann mithilfe des zuvor formulierten Induktionsgesetzes für eine Leiterschleife verstanden werden. Da die magnetischen Feldlinien die aufgespannte Fläche senkrecht durchstoßen, kann der magnetische Fluss berechnet werden als

\Phi =B_{0}\cdot A,

wobei die Fläche eine rechteckige Fläche mit dem Flächeninhalt

A=L\cdot x

ist.

Der von den Leitern eingeschlossene magnetische Fluss beträgt folglich:

\Phi =B_{0}\cdot A=B_{0}\underbrace {Lx} _{=A}=B_{0}\cdot L\cdot x

Da die Geschwindigkeit definiert ist als

v={\frac {{\text{d}}x}{{\text{d}}t}},

kann man auch schreiben:

U={\frac {{\text{d}}\Phi }{{\text{d}}t}}=B_{0}\cdot L\cdot {\frac {{\text{d}}x}{{\text{d}}t}}=B_{0}\cdot L\cdot v

Man spricht in diesem Fall von der sogenannten Bewegungsinduktion, da die Spannung einzig durch die Bewegung des Leiters entstanden ist und die zeitliche Änderung der Flussdichte keine Rolle spielte.

Bei Bewegungsinduktion lässt sich die Entstehung der Spannung immer als Folge der Lorentzkraft auf die im Leiterstab vorhandenen Leitungselektronen verstehen. Im vorliegenden Beispiel erklärt sich die Entstehung der Spannung wie folgt:

Die Lorentzkraft übt auf die Elektronen eine Kraft ${\vec {F}}_{\mathrm {L} }=q\cdot \left({\vec {v}}\times {\vec {B}}_{0}\right)$ aus, wobei $q=-1{,}602\cdot 10^{-19}\ \mathrm {C}$ die Ladung eines Elektrons und ${\vec {v}}$ die Geschwindigkeit des Elektrons ist.
Die Richtung der Kraft lässt sich mit der UVW-Regel oder der Rechte-Hand-Regel nachvollziehen. In der Zeichnung wird der Leiter von links nach rechts bewegt ( $\Rightarrow$ Daumen der rechten Hand zeigt nach rechts). Das schwachgraue Muster im Hintergrund des Bildes symbolisiert Feldlinien des Magnetfeldes ${\vec {B}}_{0}$ , die senkrecht zur Ebene der Schienenanordnung vom Betrachter weg verlaufen ( $\Rightarrow$ Zeigefinger zeigt in die Zeichenebene hinein). Der Mittelfinger zeigt dementsprechend in Richtung der Kraftrichtung, die auf positive Ladungsträger ausgeübt würde ( $\Rightarrow$ Mittelfinger zeigt von der unteren Schiene auf die obere Schiene). Folglich werden negativ geladene Elektronen zur unteren Schiene hin verschoben.
Aufgrund der Lorentzkraft verschieben sich die Elektronen so, dass auf der oberen Schiene ein Elektronenmangel und auf der unteren Schiene ein Elektronenüberschuss entsteht.
Aus der ungleichmäßigen Ladungsverteilung ergibt sich ein elektrisches Feld, das der Lorentzkraft entgegenwirkt.
Im Gleichgewichtsfall sind die Lorentzkraft ${\vec {F}}_{\mathrm {L} }$ und die Coulombkraft ${\vec {F}}_{\mathrm {C} }$ entgegengesetzt gleich, und es gilt:

{\vec {E}}=-{\vec {v}}\times {\vec {B}}_{0}

Die elektrische Feldstärke zeigt in Richtung auf die untere Schiene und erklärt die auftretende Klemmenspannung.

Beispiel: Induktion durch Flussdichteänderung

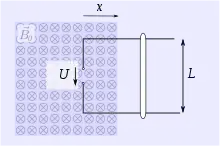
Ändert sich die Flussdichte im Leiterkreis, so zeigt das Voltmeter eine Spannung an.

Eine Änderung des magnetischen Flusses lässt sich auch dadurch erreichen, dass man die magnetische Flussdichte ändert. Dies geschieht im nebenstehenden Beispiel dadurch, dass man einen Magneten von links kommend unter der Leiterschleife hindurchschiebt. Die Darstellung wurde so gewählt, dass sich die gleiche Flussänderung wie beim Beispiel „Induktion durch Bewegung des Leiters“ ergibt. Folglich ergibt sich an den Klemmen der Anordnung auch die gleiche Spannung:

U=-{\frac {{\text{d}}\Phi }{{\text{d}}t}}=-B_{0}\cdot L{\frac {{\text{d}}x}{{\text{d}}t}}=-B_{0}\cdot L\cdot v

Obwohl bei beiden Experimenten die gleiche Flussänderung und die gleiche Spannung auftreten, unterscheiden sich beide Experimente ansonsten sehr stark. Dies gilt insbesondere im Hinblick auf das elektrische Feld: Beim Beispiel „Induktion durch Bewegung des Leiters“ liegt ein elektrostatisches Feld vor, während beim Beispiel „Induktion durch Flussdichteänderung“ ein elektrisches Feld mit starken Wirbelanteilen vorliegt.

Technische Anwendungen

Historischer Induktionsapparat aus dem Physikunterricht

In der Technik findet das Induktionsgesetz in vielfacher Hinsicht Anwendung. Allen Beispielen ist gemein, dass durch Änderung des magnetischen Flusses eine stromtreibende Wirkung erzielt wird. Dies geschieht entweder durch Bewegung eines Leiters in einem magnetischen Feld (Bewegungsinduktion) oder durch Änderungen des Magnetfeldes:

Induktionsschleife für Kfz zur Steuerung von Verkehrsampelanlagen und Schranken
Dynamisches Mikrofon
Dynamisches (Magnet-)Tonabnehmersystem für Plattenspieler
Tonabnehmer für elektrische Saiteninstrumente (z. B. E-Gitarre und E-Bass)
Tonkopf zur Abtastung von Magnetbändern
Generator = Dynamo = Lichtmaschine
RFID-Tag (beispielsweise Ski-Pass)
Transkranielle Magnetstimulation
Induktionsgeber (auch induktiver Impulsgeber) als Drehzahlsensor (z. B. im Kfz-Bereich)
Induktionshärten
Induktionslampe
Induktionssender
Transformator
Ringschleifenanlage für die Übertragung von Audiosignalen in Hörgeräte
Aufwärtswandler
Betatron
Induktions-Linearbeschleuniger
Induktive Erwärmung durch Wirbelströme: Induktionsofen, Induktionshärten, das Induktionsfeld, Induktionskochfeld

Erkennen der Flussänderung

Wenn an den Klemmen einer starren Leiterschleife eine Spannung abgreifbar ist, so kann diese dem Induktionsgesetz für Leiterschleifen entsprechend immer auf eine Flussänderung in der Leiterschleife zurückgeführt werden.

Bei der Bewegung der Leiterschleife tritt eine Flussänderung auf.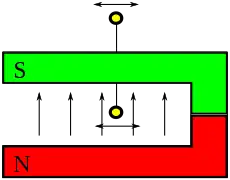
Bei der Bewegung der Leiterschleife tritt ebenfalls eine Flussänderung auf, die aber oft nicht erkannt wird.
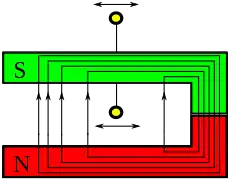Die magnetische Flussdichte in den Schenkeln des Hufeisenmagneten ist nicht konstant.

Hübel[17] weist unter dem Stichwort „Hufeisenparadoxon“ darauf hin, dass diese Flussänderung in manchen Fällen dem ungeübten Auge verborgen bleibt und diskutiert die Probleme anhand verschiedener Anordnungen mit Hufeisenmagneten, wie sie typischerweise im Schulunterricht verwendet werden (vgl. nebenstehende Bilder).

Während die Flussänderung in der Leiterschleife in der ersten Anordnung für Anfänger normalerweise leicht erkennbar ist, misslingt dies vielen Lernenden bei dem zweiten Bild. Die Lernenden konzentrieren sich auf den mit Luft erfüllten Bereich der Anordnung und berücksichtigen nicht, dass die Flussdichte zum Pol des Permanentmagneten hin nur im Innenbereich kontinuierlich zunimmt, während sie maßgeblich zu den Polen hin im Magneten abnimmt (siehe drittes Bild).

Anordnung mit Rollkontakten – Versuch von Hering

Ein Permanentmagnet wird in die Leiterschleife hineinbewegt. Obwohl in der betrachteten Fläche eine Flussänderung auftritt, schlägt das Voltmeter nicht aus.

Das nebenstehend dargestellte Experiment zum Heringschen Paradoxon,[18][19][20] benannt nach Carl Hering, zeigt, dass am Spannungsmessgerät kein Ausschlag stattfindet, obwohl bei einer bestimmten Betrachtung eine Flussänderung vorliegt.[21]

Anordnung: Ein elektrisch ideal leitfähiger Permanentmagnet wird mit der Geschwindigkeit $v$ in eine Leiterschleife hineinbewegt. Die obere und untere Kontaktfläche des Magneten sind über feststehende Rollen elektrisch leitend mit den eingezeichneten Leiterdrähten verbunden.

Paradoxon: Der scheinbare Widerspruch des Experimentes zum Induktionsgesetz ist durch eine formale Betrachtung auflösbar. Dabei führen Form I und Form II mit ruhender oder auch konvektiver (im Magneten mitwandernder) Umlaufkurve zum (gemessenen) Ergebnis, dass keine Spannung induziert wird. Die Tabelle gibt exemplarisch die Terme an, die bei Form II anfallen.

**Anordnung von C. Hering – Zwei Varianten der Spannungsberechnung**
Induktionsgesetz Form II	$\textstyle \partial {\mathcal {A}}$	$\textstyle {\vec {u}}$	$\textstyle \int _{\mathrm {C} DAB}{\vec {E}}\cdot {\text{d}}{\vec {s}}$	$\textstyle \int _{\mathrm {B} C}{\vec {E}}\cdot {\text{d}}{\vec {s}}$	$\textstyle \int \limits _{\mathrm {B} C}{\vec {u}}\times {\vec {B}}\cdot {\text{d}}{\vec {s}}$	$\textstyle -{\frac {\text{d}}{{\text{d}}t}}\int \limits _{{\mathcal {A}}(t)}{\vec {B}}\cdot {\text{d}}{\vec {A}}$
$\textstyle \oint \limits _{\partial {\mathcal {A}}}{({\vec {E}}+{\vec {u}}\times {\vec {B}})\cdot {\text{d}}{\vec {s}}}=-{\frac {\text{d}}{{\text{d}}t}}\int \limits _{\mathcal {A}}{\vec {B}}\cdot {\text{d}}{\vec {A}}\quad \quad$	ruhend	0	$\textstyle U$	$\textstyle -vBL$	0	$\textstyle -vBL$
$\textstyle \oint \limits _{\partial {\mathcal {A}}(t)}{({\vec {E}}+{\vec {u}}\times {\vec {B}})\cdot {\text{d}}{\vec {s}}}=-{\frac {\text{d}}{{\text{d}}t}}\int \limits _{{\mathcal {A}}(t)}{\vec {B}}\cdot {\text{d}}{\vec {A}}\quad \quad$	konvektiv	$\textstyle {\vec {v}}$	$\textstyle U$	$\textstyle -vBL$	$\textstyle +vBL$	0

Gegenüber dem hohen Innenwiderstand des Spannungsmessers sind die auf die ruhende Messleitung und den bewegten Magneten entfallenden Widerstände vernachlässigbar. Deshalb kann im ruhenden Teil CDAB nur im Spannungsmesser eine elektrische Feldstärke existieren, sodass dort der Beitrag zum Umlaufintegral von $\textstyle {\vec {E}}$ gleich $\textstyle U$ ist (4. Spalte der Tabelle). Der Term $\textstyle -vLB$ in der 5. Spalte rührt daher, dass der bewegte magnetisierte Körper im Laborsystem elektrisch polarisiert erscheint.[22] Der Term gibt die entsprechende elektrische Spannung an. Zum gleichen Resultat führt auch die Transformationsbeziehung zwischen elektrischer Feldstärke und magnetischer Flussdichte $\textstyle {\vec {E}}'={\vec {E}}+{\vec {v}}\times {\vec {B}}$ nach Lorentz bei $\textstyle {\vec {E}}'=0$ . In den magnetischen Schwund in der Spalte rechts außen geht die Bewegung der Randlinie ein. Bei bewegtem Abschnitt BC bleibt der Fluss konstant. Ruhende oder bewegte Randlinie führen mit den angegebenen Termen zum (auch gemessenen) Resultat $\textstyle U=0$ .

Allgemeines Induktionsgesetz in differentieller Form und in Integralform

Das Gesetz der elektromagnetischen Induktion, kurz Induktionsgesetz, beschreibt einen Zusammenhang zwischen elektrischen und magnetischen Feldern (der andere ist das Ampèresches Gesetz). Es besagt, dass bei einer Änderung des magnetischen Flusses durch eine Fläche am Rand dieser Fläche eine Ringspannung entsteht. In besonders häufig verwendeten Formulierungen wird das Induktionsgesetz beschrieben, indem die Randlinie der Fläche als unterbrochene Leiterschleife dargestellt wird, an deren offenen Enden die Spannung gemessen werden kann.

Die zum Verständnis sinnvolle Beschreibung gliedert sich in zwei mögliche Darstellungsformen:

Die Integralform oder auch globale Form des Induktionsgesetzes: Dabei werden die globalen Eigenschaften eines räumlich ausgedehnten Feldgebietes (über den Integrationsweg) beschrieben.
Die differentielle Form oder auch lokale Form des Induktionsgesetzes: Dabei werden die Eigenschaften einzelner lokaler Feldpunkte in Form von Dichten beschrieben. Die Volumina der globalen Form streben gegen null, und die auftretenden Feldstärken werden differenziert.

Beide Darstellungsformen beschreiben denselben Sachverhalt. Je nach konkretem Anwendungsfall und Problemstellung kann es sinnvoll sein, die eine oder die andere Form zu benutzen.

Bei der Anwendung des Induktionsgesetzes ist zu beachten, dass alle in den Gleichungen auftretenden Größen, d. h. die elektrische Feldstärke ${\vec {E}}$ , die magnetische Flussdichte ${\vec {B}}$ , die orientierte Fläche ${\mathcal {A}}$ , die Konturlinie $\partial {\mathcal {A}}$ dieser Fläche und die lokale Geschwindigkeit ${\vec {u}}$ eines Punktes auf der Konturlinie von einem beliebigen, aber für alle Größen gleichen, Bezugssystem (Inertialsystem) aus beschrieben werden.

Führt die Konturlinie durch Materie, ist zudem zu beachten:

Die Konturlinie $\partial {\mathcal {A}}$ ist eine gedachte Linie. Da sie keine physikalische Entsprechung hat, hat eine eventuelle zeitliche Bewegung der Konturlinie grundsätzlich keinen Einfluss auf die stattfindenden physikalischen Prozesse. Insbesondere verändert eine Bewegung der Konturlinie nicht die Feldgrößen ${\vec {E}}$ und ${\vec {B}}$ . In der Integralform I wird die Bewegung der Konturlinie daher überhaupt nicht berücksichtigt. In der Integralform II beeinflusst die Bewegung der gedachten Konturlinie beide Seiten der Gleichung in gleichem Maße, sodass man bei der Berechnung beispielsweise einer elektrischen Spannung mit Integralform I zu dem gleichen Ergebnis kommt wie bei der Berechnung derselben Spannung mithilfe von Integralform II.
Grundsätzlich darf die Geschwindigkeit der Konturlinie von der Geschwindigkeit der im Experiment verwendeten Körper (z. B. Leiterschleife, Magnete) abweichen. Die Geschwindigkeit der Konturlinie in Bezug auf den Beobachter wird im Rahmen des Artikels mit ${\vec {u}}$ gekennzeichnet, während die Geschwindigkeit von Objekten mit dem Buchstaben ${\vec {v}}$ beschrieben wird.
Im Gegensatz zur Bewegung der Konturlinie hat die Geschwindigkeit der Körper im Allgemeinen einen Einfluss auf die stattfindenden physikalischen Vorgänge. Das gilt insbesondere für die Feldgrößen ${\vec {E}}$ und ${\vec {B}}$ , die der jeweilige Beobachter misst.

Induktionsgesetz in differentieller Form

Das Induktionsgesetz in differentieller Form lautet:

\operatorname {rot} {\vec {E}}=-{\dot {\vec {B}}}

Das Vorhandensein von elektrischen Wirbeln bzw. einer zeitveränderlichen magnetischen Flussdichte ist das wesentliche Kennzeichen von Induktion. In elektrischen Feldern ohne Induktion (z. B. in dem Feld unbewegter Ladungen) existieren keine geschlossenen Feldlinien der elektrischen Feldstärke $E$ , und das Umlaufintegral der elektrischen Feldstärke ergibt immer null.

Seine Hauptanwendung findet das Induktionsgesetz in differentieller Form einerseits bei theoretischen Herleitungen und in der numerischen Feldberechnung, andererseits (jedoch seltener) in der analytischen Berechnung konkreter technischer Fragestellungen.

Wie in Einsteins erstem Werk über die spezielle Relativitätstheorie[23] gezeigt wurde, stehen die Maxwellgleichungen in differentieller Form in Übereinstimmung mit der speziellen Relativitätstheorie. Eine an den heutigen Sprachgebrauch angepasste Herleitung hierzu findet sich in dem inzwischen vergriffenen Lehrbuch von Simonyi.[24]

Übergang von der differentiellen Form zur Integralform

Der Zusammenhang zwischen der Integralform und der differentiellen Form kann mithilfe des Satzes von Stokes mathematisch beschrieben werden. Dabei werden die globalen Wirbel- und Quellenstärken in lokale, diskrete Wirbel- bzw. Quellendichten, die einzelnen Raumpunkten (Punkten eines Vektorfeldes) zugeordnet sind, übergeführt.

Ausgangspunkt ist das Induktionsgesetz in differentieller Form:

\operatorname {rot} {\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}

Zur Überführung in die integrale Form wird der Satz von Stokes verwendet, der aus naheliegenden Gründen mit der Variablen ${\vec {E}}$ formuliert wird:

\oint \limits _{\partial {\mathcal {A}}}{\vec {E}}\,{\text{d}}{\vec {s}}=\int \limits _{\mathcal {A}}\operatorname {rot} {\vec {E}}\,{\text{d}}{\vec {A}}

Ersetzt man im rechten Term des Stokesschen Gesetzes das Vektorfeld ${\vec {E}}$ entsprechend dem Induktionsgesetz in differentieller Form durch den Term $-{\tfrac {\partial {\vec {B}}}{\partial t}}$ , so ergibt sich:

\oint \limits _{\partial {\mathcal {A}}}{\vec {E}}\,{\text{d}}{\vec {s}}=-\int \limits _{\mathcal {A}}{\frac {\partial {\vec {B}}}{\partial t}}\,{\text{d}}{\vec {A}}

Das ist eine mögliche allgemeine Form des Induktionsgesetzes in Integralform,[25] die entgegen vielen anderslautenden Behauptungen sowohl für Konturlinien in ruhenden Körpern als auch in bewegten Körpern angewendet werden kann.[26]

Um eine Formulierung zu erhalten, die den magnetischen Fluss $\Phi =\int \limits _{\mathcal {A}}{\vec {B}}\,{\text{d}}{\vec {A}}$ enthält, addiert man auf beiden Seiten der Gleichung den Term $\oint \limits _{\partial {\mathcal {A}}}({\vec {u}}\times {\vec {B}})\,{\text{d}}{\vec {s}}$ . Dabei ergibt sich:

\oint \limits _{\partial {\mathcal {A}}}\left({\vec {E}}+{\vec {u}}\times {\vec {B}}\right)\,{\text{d}}{\vec {s}}=-\int \limits _{\mathcal {A}}{\frac {\partial {\vec {B}}}{\partial t}}\,{\text{d}}{\vec {A}}+\oint \limits _{\partial {\mathcal {A}}}({\vec {u}}\times {\vec {B}})\,{\text{d}}{\vec {s}}

Der rechte Teil der Gleichung entspricht wegen $\operatorname {div} {\vec {B}}=0$ der negativen zeitlichen Änderung des magnetischen Flusses,[27][28] sodass das Induktionsgesetz in Integralform in voller Allgemeingültigkeit auch folgendermaßen notiert werden kann:

\oint \limits _{\partial {\mathcal {A}}}\left({\vec {E}}+{\vec {u}}\times {\vec {B}}\right)\,{\text{d}}{\vec {s}}=-{\frac {\text{d}}{{\text{d}}t}}\int \limits _{\mathcal {A}}{\vec {B}}\,{\text{d}}{\vec {A}}

In vielen Lehrbüchern werden diese Zusammenhänge leider nicht richtig notiert, was daran erkennbar ist, dass der auf der linken Gleichungsseite notierte Term ${\vec {u}}\times {\vec {B}}$ fehlt.[29][30][31] In der neuen Auflage ist der Fehler behoben.[32] Richtig notiert wird das Induktionsgesetz hingegen beispielsweise bei Fließbach.[33][34][35]

Der Irrtum besteht wahrscheinlich darin, dass der fehlende Term irrtümlich der elektrischen Feldstärke zugeschlagen wird. (Manche Autoren sprechen in diesem Zusammenhang auch von einer effektiven elektrischen Feldstärke.)[36] In seiner Konsequenz führt das Weglassen des Terms ${\vec {u}}\times {\vec {B}}$ dazu, dass die Größe $E$ inkonsistent verwendet wird und je nach Zusammenhang eine unterschiedliche Bedeutung hat.[37]

Induktionsgesetz in Integralform

Die Spannung zwischen den beiden Punkten A und B entlang des eingezeichneten Wegs ist die Summe der Produkte

{\vec {E}}\cdot {\text{d}}{\vec {r}}

aus der elektrischen Feldstärke

{\vec {E}}

und dem Wegstückchen

{\text{d}}{\vec {r}}.

Im folgenden Abschnitt wird die erste Integralform des Induktionsgesetzes betrachtet:

\oint \limits _{\partial {\mathcal {A}}}{\vec {E}}\,\mathrm {d} {\vec {s}}=-\int \limits _{\mathcal {A}}{\frac {\partial {\vec {B}}}{\partial t}}\,\mathrm {d} {\vec {A}}

Entsprechend der mathematischen Formulierung des Integrals wird die Fläche ${\mathcal {A}}$ zu einem konstanten Zeitpunkt betrachtet und deren zeitliche Änderung nicht berücksichtigt.

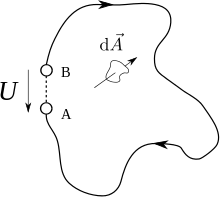
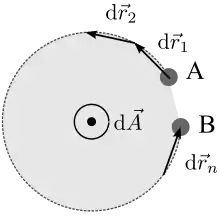
Im Hinblick auf den Begriff der induzierten Spannung – das Integral über die elektrische Feldstärke – wird zunächst die im nebenstehenden Bild eingezeichnete Verbindungslinie zwischen den Punkten A und B in einem elektrischen Feld betrachtet.

Die Spannung zwischen den Punkten A und B („äußerer Pole“ einer „Steckdose“) kann man näherungsweise berechnen, indem man den Weg in viele kleine Wegelemente ${\text{d}}{\vec {r}}$ unterteilt. Da man aufgrund der nur geringen Länge näherungsweise von einer konstanten elektrischen Feldstärke entlang eines solchen Wegstückes ausgehen kann, ergibt sich für die Teilspannung entlang eines Wegelementes im Innern der Wert

{\text{d}}U\approx +{\vec {E}}(x,y,z)\cdot {\text{d}}{\vec {r}}={+{E}_{\text{tan}}}\,{\text{d}}r.

Als Gesamtspannung zwischen beiden Punkten ergibt sich somit

\Delta U\approx +{\vec {E}}({{x}_{1}},{{y}_{1}},{{z}_{1}})\cdot {\text{d}}{{\vec {r}}_{1}}+{\vec {E}}({{x}_{2}},{{y}_{2}},{{z}_{2}})\cdot {\text{d}}{{\vec {r}}_{2}}+\dotsb +{\vec {E}}({{x}_{n}},{{y}_{n}},{{z}_{n}})\cdot {\text{d}}{{\vec {r}}_{n}}.

Die exakte Darstellung wird mithilfe eines Integrals definiert. Dieses kann man sich als Grenzwert für unendlich viele Wegstücke mit unendlich kleiner Länge $\left|{\text{d}}{\vec {r}}\right|\to 0$ vorstellen. Zur Berechnung definiert man i. A. eine von einem Parameter $\xi$ abhängige Funktion ${\vec {r}}(\xi )$ , die im Bereich $\xi =0\dots 1$ die Punkte entlang der Wegstrecke beschreibt (im Innern also in Pfeilrichtung). Die Spannung zwischen beiden Punkten kann dann über ein Kurvenintegral formal erfasst werden:

\Delta U=\int _{\xi =0}^{1}{{\vec {E}}(}{\vec {r}})\cdot {\frac {\partial {\vec {r}}(\xi )}{\partial \xi }}{\text{d}}\xi =:\int _{A}^{B}{\vec {E}}\cdot {\text{d}}{\vec {r}}\,,

berechnet in Pfeilrichtung

Lässt man nun den Punkt entlang der Kontur $C=\partial {\mathcal {A}}$ eines Gesamtumlaufes weiterwandern, bis er die eingeschlossene Fläche genau einmal umrundet hat und wieder mit Ausgangspunkt identisch wird $(B=A),$ ergibt sich als Gesamtwert die in der geschlossenen Leiterschleife induzierte Umlaufspannung $U_{\text{ind}}$ :

U_{\text{ind}}=\oint _{C}E_{\text{tan}}{\text{d}}r=\oint _{C}{\vec {E}}\cdot {\text{d}}{\vec {r}}

Hinsichtlich des Vorzeichens ist zu berücksichtigen, dass die Kontur die Fläche dabei im Sinne der Rechte-Hand-Regel umrundet.

Der dritte Ausdruck obiger Gleichungen ist dabei die dem zweiten Ausdruck gleichwertige vektorielle Darstellung des tangentialen Feldstärkeanteils mithilfe des Skalarproduktes, und die beiden Integrale sind sogenannte Ringintegrale, die immer dann verwendet werden, wenn (wie hier) längs eines geschlossenen Weges integriert wird, in diesem Fall entlang der Kontur der Leiterschleife $C.$

Die induzierte Spannung lässt sich bei einer nichtbewegten Leiterschleife näherungsweise als Spannungsabfall mit einem Spannungsmessgerät messen, wenn man entlang der geschlossenen Linie eine Leiterschleife anbringt und diese an einer Stelle auftrennt. Da über dem Leiterdraht nahezu keine elektrische Spannung abfällt, liegt die ganze induzierte Spannung zwischen den Klemmen.

Relativistische Aspekte

In Messsystemen mit bewegten Komponenten treten auch schon bei kleinen Geschwindigkeiten $v\ll c$ relativistische Effekte auf. Diese grundsätzliche Tatsache wird durch ein einfaches Gedankenexperiment deutlich:

Ein Beobachter, der eine (relativ zu ihm nicht bewegte) Ladung beobachtet, wird ein elektrisches Feld messen, jedoch aufgrund des fehlenden Stromflusses kein magnetisches Feld.
Bewegt sich der Beobachter hingegen auf die Ladung zu oder von ihr weg, so wird er einerseits bemerken, dass sich aufgrund der Bewegung das elektrische Feld verändert. Das bedeutet, dass der Beobachter bei gleicher Entfernung von der Ladung, aber anderer Relativgeschwindigkeit zur Ladung ein unterschiedliches $E$ -Feld misst. Andererseits interpretiert der Beobachter die Ladung aber auch als einen Strom, der sich von ihm fort oder auf ihn zubewegt. Der Beobachter wird also zusätzlich zum elektrischen Feld ein magnetisches Feld erkennen.

Damit bei Messungen mit bewegten Komponenten keine Missverständnisse auftreten, ist die Angabe des Bezugssystems, relativ zu dem die Beobachtungen beschrieben werden, unbedingt erforderlich. Ebenso ist es erforderlich, Größen, die in einem anderen als dem zugrunde gelegten Bezugssystem gemessen werden, mithilfe der Lorentztransformation umzurechnen.

Besonders wichtig ist die Anwendung der Lorentztransformation bei der Betrachtung elektrischer Feldstärken. Dies ist entgegen einer weit verbreiteten Ansicht schon bei Geschwindigkeiten weit unterhalb der Lichtgeschwindigkeit (beispielsweise einige mm/s) erforderlich und in praktisch allen Experimenten mit bewegten Leitern von Bedeutung.

Experiment mit einem bewegten Leiterstab im zeitlich konstanten

B

-Feld

Zur Erläuterung betrachten wir erneut den bewegten Leiterstab im zeitlich konstanten $B$ -Feld.

Da die Leiterschleife geöffnet ist, beträgt die stromtreibende Kraft ${\vec {F}}$ auf eine Ladung $q$

{\vec {F}}=q\cdot ({\vec {E}}+{\vec {v}}\times {\vec {B}}_{0})=0.

In dem mit der Geschwindigkeit ${\vec {v}}$ bewegten Leiterstab ergibt sich somit aus Sicht eines Beobachters im Laborsystem die Feldstärke

{\vec {E}}=-{\vec {v}}\times {\vec {B}}_{0}\neq 0,

während im Bereich des ruhenden Leiters mit ${\vec {v}}=0$ eine Feldstärke von

{\vec {E}}=0

herrscht.

Die Unterschiede in der Feldstärke zwischen den bewegten und den ruhenden Leiterabschnitten ergeben sich direkt aus der Lorentztransformation für die elektrische Feldstärke: Ein Beobachter, der sich mit dem bewegten Leiterstab mitbewegt, wird innerhalb des Leiterstabes eine (Eigen-)Feldstärke von

{\vec {E}}'={\vec {0}}

messen. Setzt man die (gestrichene) Eigenfeldstärke in die passende Transformationsgleichung ein, so ergibt sich für die entsprechende Größe im Laborsystem:

{\vec {E}}'=\gamma \left({\vec {E}}+{\vec {v}}\times {\vec {B}}_{0}\right)+(1-\gamma ){\frac {{\vec {E}}\cdot {\vec {v}}}{{v}^{2}}}{\vec {v}}={\vec {0}}

Wegen ${\vec {v}}\perp {\vec {E}}$ entfällt der gesamte rechte Term und damit auch die Relevanz des Faktors $\gamma$ , der gewissermaßen „in die Null hineindividiert“ werden kann. Wie erwartet ergibt sich dabei für die elektrische Feldstärke aus Sicht des Laborsystems der Wert

{\vec {E}}=-{\vec {v}}\times {\vec {B}}.

Mithilfe dieses Experimentes kann man demzufolge Relativitätstheorie mit einfachen Vorlesungsexperimenten demonstrieren. Da das genannte Experiment in vielen Darstellungen als ein Beispiel für elektromagnetische Induktion dargestellt wird, soll ausdrücklich bekräftigt werden, dass die Klemmenspannung nicht auf Wirbel des elektrischen Feldes zurückgeführt werden kann, da wegen $\operatorname {rot} {\vec {E}}={\dot {\vec {B}}}=0$ keine solchen vorhanden sind. Wie das Feldlinienbild zeigt, liegt ein reines Potentialfeld vor. Diese zeigen von positiven Ladungen auf der Oberfläche der oberen Schiene zu negativen Ladungen auf der Oberfläche der unteren Schienen. In diesem Sinne kann der physikalische Vorgang, der bei diesem Experiment stattfindet, mit dem Aufladen eines Kondensators verglichen werden.

Betrachtungen spezieller Fragestellungen

Induktionsbeispiel: Bewegter Leiterstab im Magnetfeld (mit Stromfluss)

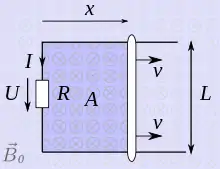
Ist die Leiterschleife geschlossen und bewegt sich der Stab im Magnetfeld, kommt es zu einem Stromfluss im Stromkreis.

In Abänderung des weiter oben diskutierten Beispiels eines „bewegten Leiterstabes im homogenen Magnetfeld“ wird hier ein Stromkreis mit endlichem Widerstand betrachtet, sodass es bei der Bewegung des Leiterstabes im Magnetfeld zu einem Stromfluss kommt. Für die Stromstärke gilt:

I={\frac {U}{R}}={\frac {\frac {{\text{d}}\Phi }{{\text{d}}t}}{R}}

Hierbei wird die gesamte Flussänderung in der Leiterschleife betrachtet. Da aber die Induktivität $L_{\Phi }\approx 0$ für eine Leiteranordnung wie hier genähert werden kann, ist auch der stromabhängige magnetische Fluss $\Phi _{L}=L_{\Phi }I\approx 0$ und die dazugehörige Flussänderung ${\tfrac {{\text{d}}\Phi _{L}}{{\text{d}}t}}=L_{\Phi }{\tfrac {{\text{d}}I}{{\text{d}}t}}\approx 0$ vernachlässigbar. Die induzierte Stromstärke ist damit:

I={\frac {vLB_{0}}{R}}

Wird der Leiterstab mit der konstanten Geschwindigkeit $v$ bewegt, wird mechanische Arbeit verrichtet. Die Kraft ist die Lorentzkraft auf einen stromdurchflossenen Leiter der Länge $L$ im Magnetfeld der Flussdichte $B_{0}$ :

{\vec {F}}=I{\vec {L}}\times {\vec {B}}_{0},

hier:

F=ILB_{0}

Für die elektrische Leistung, die im Widerstand umgesetzt wird, gilt $P=UI$ und für die mechanische Leistung einer solchen gleichförmigen Bewegung gilt $P=vF=vILB_{0}={\frac {U}{LB_{0}}}ILB_{0}=UI$ , nachdem man die entsprechenden Größen von oben eingesetzt hat. Es wird also mechanische Arbeit in elektrische umgewandelt.

Induktionsbeispiel: Leiterschleife im Magnetfeld

Eine Leiterschleife dreht sich im Magnetfeld.

Dreht sich eine Leiterschleife mit der Winkelgeschwindigkeit $\omega =2\pi f$ in einem aus dem Laborsystem betrachtet zeitlich konstanten Magnetfeld, so verändert sich aus Sicht der Leiterschleife die magnetische Flussdichte ständig, und es ergibt sich ein veränderter magnetischer Fluss durch die Leiterschleife.

Die an den Klemmen im sich drehenden System gemessene Spannung kann folgendermaßen berechnet werden:

Die durch die Leiterschleife berandete ebene Fläche hat den Flächeninhalt $A=l_{1}l_{2}$ .
Die magnetische Flussdichte ändert im Koordinatensystem des mitbewegten Beobachters ständig ihren Betrag und ihre Richtung. Nimmt man an, dass das Bild die Fläche zum Zeitpunkt $t=0$ zeigt, so beträgt der senkrecht auf die Fläche auftretende Anteil der Flussdichte $B_{\mathrm {senkr} }(t)=\cos(2\pi ft)B$ .
Der durch die Fläche $A$ hindurchstoßende magnetische Fluss beträgt dementsprechend $\Phi (t)=BA\cos(2\pi ft)$ .
Für die Spannung $U$ folgt somit mit Hilfe der Kettenregel:

U={\frac {{\text{d}}\Phi }{{\text{d}}t}}=BA(-2\pi f)\sin(2\pi ft)

Induktionsbeispiel: Induktion bei einer elektrischen Spule mit mehreren Windungen

Fläche einer Spule mit drei Windungen

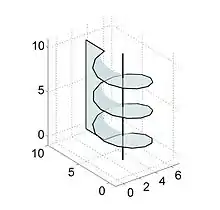
Das Induktionsgesetz ist auch für elektrische Spulen mit mehreren Windungen anwendbar. Die zur Berechnung des magnetischen Flusses erforderliche Fläche wird im nebenstehenden Bild veranschaulicht.[38] Das Induktionsgesetz in seiner allgemeinen Form erfordert daher keinen Faktor $N$ für die Windungszahl der Spule, auch wenn der Spulendraht im konkreten Fall einen Zylinder mehrfach umläuft.

In den meisten Veröffentlichungen zur elektromagnetischen Induktion bei elektrischen Spulen wird der Einfachheit halber der Faktor $N$ für die Windungszahl eingeführt, und das Induktionsgesetz wird in der Form

U={\frac {{\text{d}}\Psi }{{\text{d}}t}}\approx N{\frac {{\text{d}}\Phi _{\text{w}}}{{\text{d}}t}}

angegeben. Hierbei bezeichnet $\Psi$ den Fluss durch eine von dem Spulendraht und den Anschlüssen berandete Fläche, $\Phi _{\text{w}}$ den von einer einzelnen Windung umschlossenen magnetischen Fluss, und $U$ ist die gemessene Spannung.

Formulierungsvariante: ohmsches Gesetz für bewegte Leiter

Die Zusammenhänge bei Bewegungsinduktion lassen sich relativ leicht auch über das ohmsche Gesetz für bewegte Leiter erfassen. Im Unterschied zu einem ruhenden Leiter, bei dem ausschließlich die elektrische Feldstärke stromtreibend wirkt, wirkt auf die Ladungen in einem bewegten Leiter die komplette Lorentzkraft

{\vec {F}}_{\mathrm {L} }=q({\vec {E}}+{\vec {v}}\times {\vec {B}}).

Für nichtrelativistische Geschwindigkeiten $v\ll c$ ist die im ruhenden Bezugssystem gemessene Lorentzkraft gleich groß wie die Kraft, die die Ladung im mitbewegten System erfährt.

Für bewegte Materialien, für die das ohmsche Gesetz gilt, kann die spezifische Leitfähigkeit $\kappa$ durch die Gleichung

{\vec {J}}=\kappa ({\vec {E}}+{\vec {v}}\times {\vec {B}})

mit der elektrischen Feldstärke ${\vec {E}}$ , der Geschwindigkeit ${\vec {v}}$ des jeweiligen Leiterelements und der magnetischen Flussdichte ${\vec {B}}$ definiert werden. Das ohmsche Gesetz lautet dann wie im Falle unbewegter Materialien

{\begin{aligned}\kappa ={\text{konstant}}\end{aligned}}.

Formulierungsvariante: Zeitlich integrierte Form, Spannungszeitfläche

Die schraffierte Fläche stellt eine beispielhafte Spannungszeitfläche über die Dauer einer Viertelperiode der Sinusschwingung dar (100 % bei 325 V Scheitelspannung).

Durch Integration über die Zeit lässt sich das Induktionsgesetz für Leiterschleifen folgendermaßen umformen:

\Phi _{\text{w}}(t)=\Phi _{\text{w}}(0)+{\frac {1}{N}}\cdot \int \limits _{0}^{t}U_{\mathrm {i} }(\tau )\,{\text{d}}\tau

Diese Beziehung beschreibt den Flussverlauf als Integralfunktion des Spannungsverlaufs.

Betrachtet man den Vorgang in einem Zeitintervall von $0$ bis $T$ bei konstanter Fläche, durch die der magnetische Fluss tritt – das Zeitintervall kann sich beispielsweise über eine Halbperiode einer Wechselspannung erstrecken –, so folgt daraus für den sich dann ergebenden Fluss

\Phi _{\mathrm {w} }(T)-\Phi _{\mathrm {w} }(0)={\frac {1}{N}}\cdot \int _{0}^{T}U_{\mathrm {i} }(\tau )\,\mathrm {d} \tau .

Für den Fall $\Phi _{\mathrm {w} }(0)=0$ bedeutet das, dass der magnetische Fluss durch eine Leiterschleife bzw. eine Flussänderung in dieser, wie sie sich durch Anlegen einer Spannung nach der gegebenen Zeit $T$ dort einstellt, immer von dem Spannungszeitintegral in den angegebenen Grenzen $0$ bis $T$ verursacht sein und diesem auch entsprechen muss. Die dafür relevante Spannung ist jeweils die induzierte Spannung $U_{\mathrm {i} }$ . Diese entspricht der angelegten Spannung abzüglich ohmscher Spannungsabfälle $(I\cdot R),$ soweit diese nicht zu vernachlässigen sind.

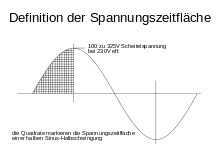
Zu veranschaulichen ist das Spannungszeitintegral auch als Fläche zwischen dem Spannungsgraphen und der Zeitachse über dem Intervall $[0;T],$ weshalb man es bisweilen auch als Spannungszeitfläche oder Spannungszeitsumme[39] bezeichnet, in meist älterer Literatur in Anlehnung an den Begriff des Kraftstoßes auch als Spannungsstoß.[40][41] Ursächlich hierfür ist der Umstand, dass messtechnisch früher die Integration von induzierten Spannungsimpulsen mittels ballistischer Galvanometer durchgeführt wurde, vgl. auch Veranschaulichung des magnetischen Kraftflusses.

Beispiel für 50 Hz bei $U_{\text{eff}}=230\,{\text{V}}$ : Auf grafische Weise durch Auszählen der kleinen Quadrate ermittelt, erhält man das Ergebnis von ca. 1,05 Voltsekunden zum Bild rechts oben, für eine Sinushalbschwingung folglich 2,1 Voltsekunden. Das ist die Spannungszeitfläche, welche die Induktion im Eisenkern eines Transformators von einem Ende der Hysteresekurve zum anderen Ende transportiert. Wenn ein Transformator passend zu den 230 V bei 50 Hz ausgelegt ist, läuft die Induktion im Dauerbetrieb hauptsächlich im senkrechten Bereich der Hysteresekurve. Höhere Spannung oder niedrigere Frequenz führt zum Übersteuern der Hysteresekurve in die waagerecht verlaufenden Bereiche, zur Kernsättigung, was dann auch in der Praxis durch den Anstieg des Magnetisierungsstromes anschaulich beobachtbar ist.

Als weiteres Beispiel kann ein vielfach praktiziertes Messprinzip für den magnetischen Fluss dienen: Hier wird der zu messende Fluss von einer Messspule erfasst und die Spannung an der Spule auf einen Integrator gegeben, der an seinem Ausgang als Ergebnis unmittelbar den Fluss anzeigt.

Formulierungsvariante: Flussregel

Die Flussregel $U_{i}=-{\dot {\Phi }}$ formuliert das Induktionsgesetz in Integralform für den Spezialfall einer Leiterschleife: Sie gilt für geschlossene Umlaufwege, die ganz in elektrisch leitendem (auch bewegtem) Material im (auch zeit- und ortsveränderlichen) Magnetfeld verlaufen, vorzugsweise in Leiterschleifen mit geringem Querschnitt. Im Fall bewegter Leiterschleifen muss sich die festgelegte Umlaufkurve zeitlich stetig und konvektiv (s. u.) ohne Unterbrechungen entwickeln. Die Geschwindigkeiten in der Anordnung müssen deutlich kleiner als die Lichtgeschwindigkeit sein.

Herleitung: Über den Umlaufweg im Induktionsgesetz Form II kann weitgehend frei verfügt werden. Im zur Flussregel führenden Ansatz wird allen Elementen ${\text{d}}{\vec {s}}$ des Umlaufwegs die lokale Stoffgeschwindigkeit ${\vec {v}}$ vorgegeben (konvektive Linienelemente, ${\vec {u}}={\vec {v}}$ ). Damit gilt:

\oint \limits _{\partial {\mathcal {A}}(t)}{({\vec {E}}+{\vec {v}}\times {\vec {B}})\cdot {\text{d}}{\vec {s}}}=-{\frac {\text{d}}{{\text{d}}t}}\int \limits _{{\mathcal {A}}(t)}{\vec {B}}\cdot {\text{d}}{\vec {A}}

.

Der Integrand des Linksterms ist nach den Transformationsgleichungen von Lorentz gleich der elektrischen Feldstärke ${\vec {E}}'$ im Ruhesystem jedes Linienelements, sodass auch

\oint \limits _{\partial {\mathcal {A}}(t)}{{\vec {E}}'\cdot {\text{d}}{\vec {s}}}=-{\frac {\text{d}}{{\text{d}}t}}\int \limits _{{\mathcal {A}}(t)}{\vec {B}}(t)\cdot {\text{d}}{\vec {A}}\quad (*)

oder kürzer

U_{i}=-{\dot {\Phi }}

geschrieben werden kann. Die letzten beiden gleichwertigen Gleichungen sind zunächst für die oben genannten Voraussetzungen zugeschnittene Formen des Induktionsgesetzes. Die letzte Gleichung wird als Flussregel[42][43] bezeichnet, wenn sie auf einen unverzweigten Stromkreis angewandt wird.[44] Die als induzierte Spannung[45][46] bezeichnete stromtreibend wirkende elektromagnetische Größe $U_{i}$ – ihrer Definition nach eine Ringspannung – erweist sich als wertgleich mit dem magnetischen Schwund $-{\dot {\Phi }}$ . Ein irgendwo im Leiterkreis eingebauter Spannungsmesser, dessen Innenwiderstand groß gegen den Widerstand des restlichen Kreises ist, zeigt den Wert von $U_{i}$ an.[47]

Dass der magnetische Schwund $-{\dot {\Phi }}$ (in Gl. ( $*$ ) der Rechtsterm) einen elektrischen Strom durch den elektrischen Widerstand in der Leiterschleife antreiben kann, illustriert die Form des Linksterms: Dort steht die ladungsbezogene Arbeit, welche die Lorentzkraft an der Ladung bei einem Schleifenumlauf verrichtet. Der Anwendungskomfort der Flussregel liegt darin, dass die stromtreibende induzierte Spannung $U_{i}$ in einer ruhenden oder auch bewegten Leiterschleife allein aus dem Magnetfeld bestimmt werden kann: Die elektrische Feldstärke im Laborsystem ${\vec {E}}$ und jene im Ruhesystem der Linienelemente ${\vec {E}}'$ kommt in der Formel nicht vor.

Die Wicklungen von Transformatoren, Elektromotoren und Generatoren zur Stromerzeugung sind Leiterschleifen im Sinne der Flussregel.

Beispiel Atmende Leiterschleife

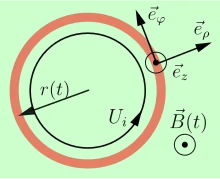
Leiterschleife mit zeitveränderlichem Radius (atmend) im zeitveränderlichen Magnetfeld

Die rechts skizzierte kreisringförmige (elastisch gedachte) Leiterschleife mit zeitveränderlichem Radius $r(t)$ befindet sich in einem homogenen, zeitabhängigen Magnetfeld ${\vec {B}}=B(t){\vec {e}}_{z}$ . Der Leiterquerschnitt $A$ und die elektrische Leitfähigkeit $\kappa$ können längs des Umfangs variieren. Die zeitliche Ableitung ${\dot {r}}=v$ des Radius $r$ erweist sich als die lokale, radial gerichtete Geschwindigkeit $v$ der Ringelemente. Die Schleifenebene liegt normal zur $z$ -Achse und bleibt parallel zu sich selbst. In der Skizze bezeichnen die Pfeile für den radialen, peripheren und axialen Einheitsvektor ${\vec {e}}_{\rho }$ , ${\vec {e}}_{\varphi }$ bzw. ${\vec {e}}_{z}$ auch die Bezugsrichtungen für die in Frage kommenden skalaren Größen. Alle im Folgenden angegebenen Feldgrößen sind zeitabhängig, was die Notation nicht jedes Mal wiederholt.

Die in der Schleife induzierte Spannung $U_{i}=-{\dot {\Phi }}=-{\tfrac {\text{d}}{{\text{d}}t}}(B{\vec {e}}_{z}\cdot \pi r^{2}{\vec {e}}_{z})=-{\dot {B}}\pi r^{2}-B\pi 2rv$ treibt darin einen elektrischen Strom $I=U_{i}/R$ an mit $R=\oint _{\partial {\mathcal {A}}}{\tfrac {{\text{d}}s}{\kappa A}}$ . Dessen felderzeugende Wirkung ist als vernachlässigbar oder schon in ${\vec {B}}(t)$ enthalten vorausgesetzt.

Die elektrischen Feldgrößen, die aus der Flussregel eliminiert sind, werden im Folgenden nur zur Information angegeben. Für die Stromdichte und die elektrische Feldstärke im Ruhesystem der Ringelemente gilt ${\vec {S}}={\vec {e}}_{\varphi }I/A$ bzw. ${\vec {E}}'={\vec {S}}/\kappa$ . Für die elektrische Feldstärke im Ruhesystem des Schleifenzentrums erhält man mit ${\vec {E}}={\vec {E}}'-{\vec {v}}\times {\vec {B}}$ das Resultat ${\vec {E}}=(S/\kappa +vB){\vec {e}}_{\varphi }$ . Die letzte Gleichung folgt mit ${\vec {v}}\times {\vec {B}}=v{\vec {e}}_{\rho }\times B{\vec {e}}_{z}=-Bv{\vec {e}}_{\varphi }$ . Für den Fall, dass der Leiterquerschnitt und die Leitfähigkeit am Umfang konstant sind, spiegelt sich die Rotationssymmetrie der Anordnung auch in den Feldgrößen. Man erhält dann die Feldkoordinaten $E'=U_{i}/(2\pi r)=-{\dot {B}}r/2-Bv$ und $E=-{\dot {B}}r/2$ .

Beispiel Spannung im Wirbelfeld

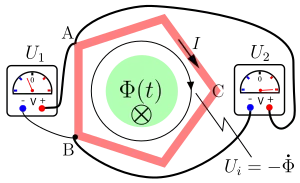
Mehrdeutigkeit der elektrischen Spannung im zeitveränderlichen Magnetfeld. Die Zeichen + und − sind Gravuren auf den Voltmetergehäusen.

Die Anordnung rechts illustriert auf Basis der Flussregel, dass die an einer (mit einem zeitveränderlichen Magnetfeld verketteten) Leiterschleife abgegriffene Spannung von der Platzierung der Messleitungen abhängt. Die Spannung zwischen zwei Punkten ist dann kein eindeutiger Begriff mehr.

In dem Messaufbau kontaktieren zwei gleich gepolte Spannungsmesser die Punkte A und B eines leitenden Rahmens in der Form eines regelmäßigen Fünfecks. Sein ohmscher Widerstand beträgt $5R$ . In der Leiterschleife treibt die induzierte Spannung $U_{i}=-{\dot {\Phi }}$ den Strom $I=U_{i}/(5R)$ an. Mit dem Umlaufweg durch das Messgerät 1 und die Rahmenseite AB ist kein Fluss verkettet. Der Spannungsmesser 1 zeigt entsprechend der Spannungsgleichung $-U_{1}-RI=0$ den Wert $U_{1}=-U_{i}/5$ an. Mit dem alternativen Umlauf A–C–B–Voltmeter1 zur Berechnung von $U_{1}$ ist der zeitveränderliche magnetische Fluss $\Phi (t)$ verkettet, sodass die Spannungsgleichung $4RI-U_{1}=U_{i}\,(=-{\dot {\Phi }})$ gilt. Daraus folgt mit $RI=U_{i}/5$ wieder $U_{1}=-U_{i}/5$ .

Für den Spannungsmesser 2 gelten entsprechende Gleichungen: Jene ohne verketteten Fluss entlang A–Voltmeter2–B–C–A lautet $U_{2}-4RI=0$ . Der alternative Umlauf A–Voltmeter2–B–A mit der Spannungsgleichung $U_{2}+RI=U_{i}$ ist mit dem Fluss $\Phi (t)$ verkettet. Aus beiden Umläufen errechnet man $U_{2}=(4/5)U_{i}$ .

Der kein Rahmenteil durchlaufende (Vergleichs-)Umlauf nur über die beiden Spannungsmesser liefert die Gleichung $-U_{1}+U_{2}=U_{i}$ , die mit den oben angegebenen Termen für $U_{1}$ und $U_{2}$ erfüllt ist.

Selbstinduktion

Literatur

Karl Küpfmüller, Gerhard Kohn: Theoretische Elektrotechnik und Elektronik. 14. Auflage. Springer, 1993, ISBN 3-540-56500-0.
Adolf J. Schwab: Begriffswelt der Feldtheorie. Elektromagnetische Felder, Maxwell-Gleichungen, Gradient, Rotation, Divergenz. 6. Auflage. Springer, 2002, ISBN 3-540-42018-5.
Heinrich Frohne, Karl-Heinz Löcherer, Hans Müller, Thomas Marienhausen, Dieter Schwarzenau: Moeller Grundlagen der Elektrotechnik (Studium). 22. Auflage. Vieweg + Teubner Verlag, Springer Fachmedien, Berlin/ Offenbach 2011, ISBN 978-3-8348-0898-1, S. 252 ff.

Weblinks

Elektromagnetische Induktion. Induktion auf Schülerniveau bei LeiFi-Physik.
Helmut Haase: Spannungsinduktion und Flussregel. (Memento vom 29. August 2014 im Internet Archive). (PDF; 21 Seiten; 2,5 MB).
Video: Induktion in ruhenden Leitern. Institut für den Wissenschaftlichen Film (IWF) 2004, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.3203/IWF/C-14868.
Video: Induktion in bewegten Leitern. Institut für den Wissenschaftlichen Film (IWF) 2004, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.3203/IWF/C-14869.

Einzelnachweise und Fußnoten

Douglas C. Giancoli: Physics: Principles with Applications. 5. Auflage. 1998, S. 623–624.
Fawwaz Ulaby: Fundamentals of applied electromagnetics. 5. Auflage. Pearson Prentice Hall, 2007, ISBN 978-0-13-241326-8, S. 255.
Joseph Henry. (Nicht mehr online verfügbar.) In: Distinguished Members Gallery, National Academy of Sciences. Archiviert vom Original am 13. Dezember 2013; abgerufen am 30. November 2006.
Bence Jones: The Life And Letters Of Faraday. Volume II, 2008, ISBN 978-1-4437-1530-0 (eingeschränkte Vorschau in der Google-Buchsuche).
Leslie Pearce Williams: Michael Faraday. A biography. Chapman and Hall, London 1965, S. 182–183 (englisch).
Leslie Pearce Williams: Michael Faraday: A biography. Chapman and Hall, London 1965, S. 191–195 (englisch).
Michael Faraday: Experimental Researches in Electricity. In: Royal Society of London (Hrsg.): Philosophical Transactions of the Royal Society of London for the Year MDCCCXXXII. Band V. Richard Taylor, London 1832, S. 154 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 4. Juli 2012]).
Zum Thema Batterie siehe auch W. Döring: Einführung in die Theoretische Physik. Band 2, Berlin 1965.
Thomas Valone: The Homopolar Handbook. A Definitive Guide to Faraday Disk and N-Machine Technologies. Abschnitt: Historical Development of the Field Rotation Paradox. (Auszug in der Google-Buchsuche)
Kleinster Elektromotor der Welt. Bei: experimentis.de.
Unipolarmotor – der einfachste Elektromotor der Welt. (Memento vom 12. Januar 2016 im Internet Archive) Bei: magnetladen.de. (PDF; 154 kB).
Die Kontroverse lässt sich auflösen, wenn man die Geschwindigkeiten konsequent auf das zugrundegelegte Bezugssystem bezieht, die Lorentztransformation für die mechanischen und elektromagnetischen Feldgrößen berücksichtigt und zudem eine ggf. vorhandene Geschwindigkeit des Voltmeters mit in die Überlegungen einbezieht.
Horst Hübel: Was ist elektromagnetische Induktion? Eine physikalisch-didaktische Analyse. Website.
Bei der Darstellung des Induktionsgesetzes in integraler Form am Artikelbeginn sind einer üblichen Konvention der Mathematik folgend die Umlaufrichtungen der Randlinie $\partial {\mathcal {A}}$ und die zugehörige Fläche ${\mathcal {A}}$ rechtshändig zueinander orientiert. Es ergibt sich dann ein negatives Vorzeichen im Induktionsgesetz.
… bzw. die Messspitze des Oszilloskops
… bzw. der Masseanschluss des Oszilloskops
Horst Hübel: Was ist elektromagnetische Induktion? Eine physikalisch-didaktische Analyse. S. 6–7, Link zum Lehrtext (PDF; 1,3 MB), Link zur Internetseite.
Proc. Am. J. E. F., März 1908, S. 339.
El. World. Nr. 11, 14. März 1908, S. 558.
The Electrician. 3. April 1908, S. 946.
H. Grabinski: Der Heringsche Versuch: Mythen und Fakten. Band 80. Springer, 1997, S. 285–290, doi:10.1007/BF01370965.
Fritz Sauter (Hrsg.): Richard Becker: Theorie der Elektrizität 1. 21. Auflage. B. G. Teubner, Stuttgart 1973, ISBN 3-519-23006-2, Abschn. 11.3
Albert Einstein: Zur Elektrodynamik bewegter Körper. In: Annalen der Physik und Chemie. 17, 30. Juni 1905, S. 891–921.
K. Simonyi: Theoretische Elektrotechnik. 9. Auflage. VEB Deutscher Verlag der Wissenschaften, Berlin 1989, Kap. 5.2.2.
Klaus W. Kark: Antennen und Strahlungsfelder. Elektromagnetische Wellen auf Leitungen im Freiraum und ihre Abstrahlung. 3. Auflage. Vieweg+Teubner, Wiesbaden 2010, Kap. 3.8.3, S. 47.
R. Kröger, R. Unbehauen: Zur Theorie der Bewegungsinduktion. Mitteilung des Lehrstuhls für Allgemeine und Theoretische Elektrotechnik, Universität Erlangen-Nürnberg, AEÜ, Band 36, Heft 9, 1982. Die Autoren erklären: „Umgekehrt gelten insbesondere die Gl. (17a, b) (das sind das Induktionsgesetz in differentieller Form und das vorgenannte Induktionsgesetz in Integralform, Anm.) entgegen allen anders lautenden Behauptungen auch für bewegte Leiter (allgemein für bewegte Medien).“
K. Simonyi: Theoretische Elektrotechnik. 9. Auflage. VEB Deutscher Verlag der Wissenschaften, Berlin 1989, Kap. 1.5.3, bewegte Medien.
H. Flanders: Differentiation under the integral sign. In: American Mathematical Monthly. 80 (6), Juni–Juli 1973, S. 615–627:
${\frac {\text{d}}{{\text{d}}t}}\int \limits _{\mathcal {A}}{\vec {B}}\cdot {\text{d}}{\vec {A}}=\int \limits _{\mathcal {A}}{\frac {\partial {\vec {B}}}{\partial t}}\cdot {\text{d}}{\vec {A}}+\oint \limits _{\partial {\mathcal {A}}}({\vec {B}}\times {\vec {u}})\cdot {\text{d}}{\vec {s}}+\int \limits _{\mathcal {A}}(\nabla \cdot {\vec {B}})\cdot {\vec {u}}\cdot {\text{d}}{\vec {A}}$
Wegen $\nabla \cdot \mathbf {B} =0$ (Nichtexistenz von magnetischen Monopolen) ist der letzte Term im Zusammenhang mit $B$ -Feldern gleich null und kann damit entfallen.
Albrecht Lindner: Grundkurs theoretische Physik. 2. erw. Auflage, ISBN 3-519-13095-5 (Auszug in der Google-Buchsuche).
E. Hering, K.-H. Modler: Grundwissen des Ingenieurs. 14. Auflage. 2007, ISBN 978-3-446-22814-6 (Auszug in der Google-Buchsuche).
W. Nerreter: Grundlagen der Elektrotechnik. Hanser-Verlag, 2006, ISBN 3-446-40414-7 (Auszug in der Google-Buchsuche).
W. Nerreter: Grundlagen der Elektrotechnik. Hanser-Verlag, 2020, ISBN 978-3-446-46456-8.
Torsten Fließbach: Elektrodynamik. Lehrbuch zur Theoretischen Physik II. 6. Auflage. Spektrum Akademischer Verlag, Heidelberg 2012, Gl. 16.8, Gl. 16.12, ISBN 978-3-8274-3035-9.
Skript zur Theoretischen Physik an der Universität Wien.
Skript der TU München zur Elektrodynamik. (Memento vom 3. März 2013 im Internet Archive).
Hier ist auch die in diesem Artikel bereits genannte Analogie mit einer Batterie nützlich: Im Zusammenhang mit Batterien spricht man statt von elektrischen Feldern von sog. elektromotorischen Kräften, und es tritt auch hier das bereits angesprochene Vorzeichenproblem auf (der elektrische Strom ist parallel, nicht antiparallel zu diesen Kräften).
R. Kröger, R. Unbehauen: Zur Theorie der Bewegungsinduktion. Mitteilung des Lehrstuhls für Allgemeine und Theoretische Elektrotechnik, Universität Erlangen-Nürnberg, AEÜ, Band 36, Heft 9, 1982. Die Autoren kritisieren, dass die Bedeutung des Buchstaben ${\vec {E}}$ für die elektrische Feldstärke dadurch inkonsistent verwendet wird und bekräftigen, dass die im Ruhesystem beobachtete magnetische Kraft nicht auf eine elektrische Feldstärke (gemessen im Ruhesystem) zurückgeführt werden kann. Wörtlich heißt es: „Die Größe ${\vec {E}}_{1}={\vec {u}}\times {\vec {B}}$ ist also im Laborsystem keine legitime elektrische Feldstärke. Sie hätte als solche in der Situation von Bild 1 auch eine seltsame stets übersehene Eigenschaft, nämlich Quellen bei negativen und Senken bei positiven Ladungen! Man kann eben nicht alles, was die Dimension der elektrischen Feldstärke hat, als solche bezeichnen. Es sei denn, man verzichtet darauf, überall in der Elektrodynamik unter ‚E‘ das gleiche zu verstehen.“
Herman A. Haus: Electromagnetic fields and Energy. Kap. 8.4, Internetlink.
Grimsehl: Lehrbuch der Physik. Band II, Leipzig 1954, S. 321–323.
Christian Gerthsen: Physik. 4. Auflage. Springer, Berlin 1956, S. 258.
Adalbert Prechtl: Vorlesungen über die Grundlagen der Elektrotechnik. Band 2, Springer, 2007, S. 121.
R. P. Feynman: Lectures on Physics. Vol. II, Chpt. 16.
R. P. Feynman: Lectures on Physics. Vol. II, Chpt. 17.
Bei der Bildung der zeitlichen Ableitung des magnetischen Flusses ist darauf zu achten, dass sich der Flächenrand (d. h. die Umlaufkurve) überall nach Maßgabe der konvektiven Randelemente verschiebt.
DIN 1324, Teil 1, Abschn. 7.3: Induzierte Spannung.
DKE-IEV Deutsche Online-Ausgabe des IEV: Induzierte Spannung.
$U_{i}$ wurde früher als elektromotorische Kraft (EMK) bezeichnet. Im angelsächsischen Raum, z. B. bei R. P. Feynman (s. o.) heißt die induzierte Spannung „(induced) electromotive force (EMF ${\mathcal {E}}$ )“.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Giancoli-1] Douglas C. Giancoli: Physics: Principles with Applications. 5. Auflage. 1998, S. 623–624.

[2] Fawwaz Ulaby: Fundamentals of applied electromagnetics. 5. Auflage. Pearson Prentice Hall, 2007, ISBN 978-0-13-241326-8, S. 255.

[3] Joseph Henry. (Nicht mehr online verfügbar.) In: Distinguished Members Gallery, National Academy of Sciences. Archiviert vom Original am 13. Dezember 2013; abgerufen am 30. November 2006.

[4] Bence Jones: The Life And Letters Of Faraday. Volume II, 2008, ISBN 978-1-4437-1530-0 (eingeschränkte Vorschau in der Google-Buchsuche).

[5] Leslie Pearce Williams: Michael Faraday. A biography. Chapman and Hall, London 1965, S. 182–183 (englisch).

[6] Leslie Pearce Williams: Michael Faraday: A biography. Chapman and Hall, London 1965, S. 191–195 (englisch).

[7] Michael Faraday: Experimental Researches in Electricity. In: Royal Society of London (Hrsg.): Philosophical Transactions of the Royal Society of London for the Year MDCCCXXXII. Band V. Richard Taylor, London 1832, S. 154 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 4. Juli 2012]).

[8] Zum Thema Batterie siehe auch W. Döring: Einführung in die Theoretische Physik. Band 2, Berlin 1965.

[9] Thomas Valone: The Homopolar Handbook. A Definitive Guide to Faraday Disk and N-Machine Technologies. Abschnitt: Historical Development of the Field Rotation Paradox. (Auszug in der Google-Buchsuche)

[10] Kleinster Elektromotor der Welt. Bei: experimentis.de.

[11] Unipolarmotor – der einfachste Elektromotor der Welt. (Memento vom 12. Januar 2016 im Internet Archive) Bei: magnetladen.de. (PDF; 154 kB).

[12] Die Kontroverse lässt sich auflösen, wenn man die Geschwindigkeiten konsequent auf das zugrundegelegte Bezugssystem bezieht, die Lorentztransformation für die mechanischen und elektromagnetischen Feldgrößen berücksichtigt und zudem eine ggf. vorhandene Geschwindigkeit des Voltmeters mit in die Überlegungen einbezieht.

[13] Horst Hübel: Was ist elektromagnetische Induktion? Eine physikalisch-didaktische Analyse. Website.

[14] Bei der Darstellung des Induktionsgesetzes in integraler Form am Artikelbeginn sind einer üblichen Konvention der Mathematik folgend die Umlaufrichtungen der Randlinie $\partial {\mathcal {A}}$ und die zugehörige Fläche ${\mathcal {A}}$ rechtshändig zueinander orientiert. Es ergibt sich dann ein negatives Vorzeichen im Induktionsgesetz.

[15] … bzw. die Messspitze des Oszilloskops

[16] … bzw. der Masseanschluss des Oszilloskops

[17] Horst Hübel: Was ist elektromagnetische Induktion? Eine physikalisch-didaktische Analyse. S. 6–7, Link zum Lehrtext (PDF; 1,3 MB), Link zur Internetseite.

[18] Proc. Am. J. E. F., März 1908, S. 339.

[19] El. World. Nr. 11, 14. März 1908, S. 558.

[20] The Electrician. 3. April 1908, S. 946.

[21] H. Grabinski: Der Heringsche Versuch: Mythen und Fakten. Band 80. Springer, 1997, S. 285–290, doi:10.1007/BF01370965.

[22] Fritz Sauter (Hrsg.): Richard Becker: Theorie der Elektrizität 1. 21. Auflage. B. G. Teubner, Stuttgart 1973, ISBN 3-519-23006-2, Abschn. 11.3

[23] Albert Einstein: Zur Elektrodynamik bewegter Körper. In: Annalen der Physik und Chemie. 17, 30. Juni 1905, S. 891–921.

[24] K. Simonyi: Theoretische Elektrotechnik. 9. Auflage. VEB Deutscher Verlag der Wissenschaften, Berlin 1989, Kap. 5.2.2.

[25] Klaus W. Kark: Antennen und Strahlungsfelder. Elektromagnetische Wellen auf Leitungen im Freiraum und ihre Abstrahlung. 3. Auflage. Vieweg+Teubner, Wiesbaden 2010, Kap. 3.8.3, S. 47.

[26] R. Kröger, R. Unbehauen: Zur Theorie der Bewegungsinduktion. Mitteilung des Lehrstuhls für Allgemeine und Theoretische Elektrotechnik, Universität Erlangen-Nürnberg, AEÜ, Band 36, Heft 9, 1982. Die Autoren erklären: „Umgekehrt gelten insbesondere die Gl. (17a, b) (das sind das Induktionsgesetz in differentieller Form und das vorgenannte Induktionsgesetz in Integralform, Anm.) entgegen allen anders lautenden Behauptungen auch für bewegte Leiter (allgemein für bewegte Medien).“

[27] K. Simonyi: Theoretische Elektrotechnik. 9. Auflage. VEB Deutscher Verlag der Wissenschaften, Berlin 1989, Kap. 1.5.3, bewegte Medien.

[28] H. Flanders: Differentiation under the integral sign. In: American Mathematical Monthly. 80 (6), Juni–Juli 1973, S. 615–627:
${\frac {\text{d}}{{\text{d}}t}}\int \limits _{\mathcal {A}}{\vec {B}}\cdot {\text{d}}{\vec {A}}=\int \limits _{\mathcal {A}}{\frac {\partial {\vec {B}}}{\partial t}}\cdot {\text{d}}{\vec {A}}+\oint \limits _{\partial {\mathcal {A}}}({\vec {B}}\times {\vec {u}})\cdot {\text{d}}{\vec {s}}+\int \limits _{\mathcal {A}}(\nabla \cdot {\vec {B}})\cdot {\vec {u}}\cdot {\text{d}}{\vec {A}}$
Wegen $\nabla \cdot \mathbf {B} =0$ (Nichtexistenz von magnetischen Monopolen) ist der letzte Term im Zusammenhang mit $B$ -Feldern gleich null und kann damit entfallen.

[29] Albrecht Lindner: Grundkurs theoretische Physik. 2. erw. Auflage, ISBN 3-519-13095-5 (Auszug in der Google-Buchsuche).

[30] E. Hering, K.-H. Modler: Grundwissen des Ingenieurs. 14. Auflage. 2007, ISBN 978-3-446-22814-6 (Auszug in der Google-Buchsuche).

[31] W. Nerreter: Grundlagen der Elektrotechnik. Hanser-Verlag, 2006, ISBN 3-446-40414-7 (Auszug in der Google-Buchsuche).

[32] W. Nerreter: Grundlagen der Elektrotechnik. Hanser-Verlag, 2020, ISBN 978-3-446-46456-8.

[33] Torsten Fließbach: Elektrodynamik. Lehrbuch zur Theoretischen Physik II. 6. Auflage. Spektrum Akademischer Verlag, Heidelberg 2012, Gl. 16.8, Gl. 16.12, ISBN 978-3-8274-3035-9.

[34] Skript zur Theoretischen Physik an der Universität Wien.

[35] Skript der TU München zur Elektrodynamik. (Memento vom 3. März 2013 im Internet Archive).

[36] Hier ist auch die in diesem Artikel bereits genannte Analogie mit einer Batterie nützlich: Im Zusammenhang mit Batterien spricht man statt von elektrischen Feldern von sog. elektromotorischen Kräften, und es tritt auch hier das bereits angesprochene Vorzeichenproblem auf (der elektrische Strom ist parallel, nicht antiparallel zu diesen Kräften).

[37] R. Kröger, R. Unbehauen: Zur Theorie der Bewegungsinduktion. Mitteilung des Lehrstuhls für Allgemeine und Theoretische Elektrotechnik, Universität Erlangen-Nürnberg, AEÜ, Band 36, Heft 9, 1982. Die Autoren kritisieren, dass die Bedeutung des Buchstaben ${\vec {E}}$ für die elektrische Feldstärke dadurch inkonsistent verwendet wird und bekräftigen, dass die im Ruhesystem beobachtete magnetische Kraft nicht auf eine elektrische Feldstärke (gemessen im Ruhesystem) zurückgeführt werden kann. Wörtlich heißt es: „Die Größe ${\vec {E}}_{1}={\vec {u}}\times {\vec {B}}$ ist also im Laborsystem keine legitime elektrische Feldstärke. Sie hätte als solche in der Situation von Bild 1 auch eine seltsame stets übersehene Eigenschaft, nämlich Quellen bei negativen und Senken bei positiven Ladungen! Man kann eben nicht alles, was die Dimension der elektrischen Feldstärke hat, als solche bezeichnen. Es sei denn, man verzichtet darauf, überall in der Elektrodynamik unter ‚E‘ das gleiche zu verstehen.“

[38] Herman A. Haus: Electromagnetic fields and Energy. Kap. 8.4, Internetlink.

[39] Grimsehl: Lehrbuch der Physik. Band II, Leipzig 1954, S. 321–323.

[40] Christian Gerthsen: Physik. 4. Auflage. Springer, Berlin 1956, S. 258.

[41] Adalbert Prechtl: Vorlesungen über die Grundlagen der Elektrotechnik. Band 2, Springer, 2007, S. 121.

[42] R. P. Feynman: Lectures on Physics. Vol. II, Chpt. 16.

[43] R. P. Feynman: Lectures on Physics. Vol. II, Chpt. 17.

[44] Bei der Bildung der zeitlichen Ableitung des magnetischen Flusses ist darauf zu achten, dass sich der Flächenrand (d. h. die Umlaufkurve) überall nach Maßgabe der konvektiven Randelemente verschiebt.

[45] DIN 1324, Teil 1, Abschn. 7.3: Induzierte Spannung.

[46] DKE-IEV Deutsche Online-Ausgabe des IEV: Induzierte Spannung.

[47] $U_{i}$ wurde früher als elektromotorische Kraft (EMK) bezeichnet. Im angelsächsischen Raum, z. B. bei R. P. Feynman (s. o.) heißt die induzierte Spannung „(induced) electromotive force (EMF ${\mathcal {E}}$ )“.