Energieniveau
Ein Energieniveau ist die diskrete Energie, die als Energieeigenzustand zu einem quantenmechanischen Zustand eines Systems (etwa eines Atoms oder eines Atomkerns) gehört. Energieniveaus sind Eigenwerte des Hamilton-Operators, sie sind deshalb zeitunabhängig. Das System kann sich dauerhaft nur in einem dieser Zustände, aber nicht bei anderen, dazwischen liegenden Werten der Energie „aufhalten“. Das tiefste Energieniveau wird als Grundzustand bezeichnet (bzw. im Falle von Entartung als "Grundzustände"), alle anderen Niveaus heißen angeregte Zustände.
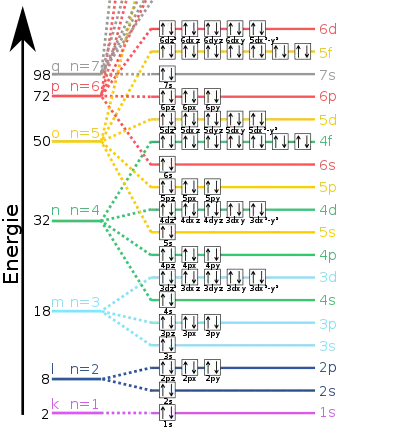
Anschaulich kann man sich vorstellen, dass Anordnung und Bewegungsweise der Elektronen in der Atomhülle – oder der Nukleonen im Kern – jeweils nur in ganz bestimmter Form stabil sind. Jeder dieser Zustände hat einen anderen, bestimmten Energieinhalt. Allerdings gibt es oberhalb einer bestimmten Grenzenergie auch ein Energie-Kontinuum, einen Bereich beliebiger möglicher Energiewerte.
In einem konservativen Feld, etwa im Coulombfeld in der Atomhülle, entspricht diese Grenze gerade der Bindungsenergie des am leichtesten abtrennbaren Teilchens (siehe z. B. Ionisation). Das Kontinuum möglicher Energien ergibt sich daraus, dass dieses abgetrennte Teilchen mit einer beliebigen kinetischen Energie davonfliegen kann. In anderen Feldern, etwa für die Nukleonen des Atomkerns, fällt die Kontinuumsgrenze nicht mit der Bindungsenergie eines Teilchens zusammen.
In beiden Fällen kann es auch im Kontinuum Energieniveaus geben, die sich etwa als Resonanzen in Wirkungsquerschnitten bemerkbar machen. In Atomen tritt dies auf, wenn ein Zustand mit einem asymptotisch freien Teilchen entartet – also energiegleich ist mit einem Zustand ohne asymptotisch freies Teilchen.
Übergänge zwischen Energieniveaus
Zu höherer Energie
Energieaufnahme in das System kann nur durch Wechsel in ein höheres Energieniveau oder in das Kontinuum erfolgen. Dies geschieht beispielsweise durch Absorption eines Photons oder durch unelastischen Stoß eines Teilchens wie beim Franck-Hertz-Versuch. Bei Übergängen zwischen diskreten Niveaus muss dabei der jeweils passende Energiebetrag zugeführt werden; der Vorgang heißt Anregung. Er führt zu diskreten Absorptionslinien im Spektrum.
Zu niedrigerer Energie
Der umgekehrte Übergang von einem höheren auf ein tieferes Niveau unter Abgabe eines Photons kann im Atom durch spontane oder von außen stimulierte Emission erfolgen.
Spontan
Der spontane Prozess wird Zerfall des angeregten Zustands oder spontane Emission genannt. Er ist ähnlich wie der radioaktive Zerfall durch eine Halbwertszeit charakterisiert. Die Energie der abgegebenen Photonen entspricht der Energiedifferenz zwischen den beiden beteiligten Energieniveaus. Dies bewirkt die diskreten Spektrallinien im Emissionsspektrum angeregter Atome und Moleküle.
Stimuliert
Ein Emissionsvorgang, der nicht spontan erfolgt, ist die Stimulierte Emission, die beim Laser ausgenutzt wird.
Allgemein
Mathematisch wird ein quantenmechanischer Übergang mit Hilfe des Übergangsdipolmoments berechnet, welche den zeitlichen und örtlichen Verlauf des quantenmechanisch superponierten Mischzustandes aus Grund- und angeregten Zustand beschreibt. Wegen der Auswahlregeln sind z. T. nicht alle Übergänge erlaubt.
Angeregte Zustände und Zerfall unter Emission elektromagnetischer Strahlung, d. h. Übergänge in Richtung höherer und in Richtung niedrigerer Energie, gibt es nicht nur bei Atomen, sondern auch bei Atomkernen. Bei diesen sind die Energiedifferenzen der Zustände deutlich höher. Hier entsteht durch spontane Emission daher die energiereiche Gammastrahlung.
Energieniveaus im Atom
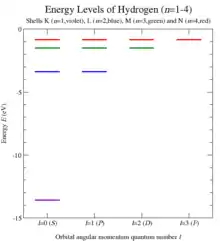
Die Energieniveaus der Atome werden durch die Hauptquantenzahl beschrieben. Die Energie des Zustands mit der Quantenzahl in einem wasserstoffähnlichen Atom der Ordnungszahl ist näherungsweise
mit der Rydberg-Energie .
Dazu kommen noch Feinstruktur- und Hyperfeinstruktur-Korrekturen und der Lamb-Shift.
Literatur
- Paul A. Tipler, Gene Mosca: Physik: für Wissenschaftler und Ingenieure. Springer-Verlag, 2014, ISBN 978-3-642-54166-7 (google.de [abgerufen am 3. September 2020]).