Kennedy-Thorndike-Experiment
Das Kennedy-Thorndike-Experiment (1932) sollte nachweisen, ob die Änderung der Geschwindigkeit des Beobachters in verschiedenen Inertialsystemen einen Einfluss auf die Ausbreitung des Lichtes hat.[1] Es ist eine Variante des Michelson-Morley-Experiments, bei der die Seitenarme des benutzten Interferometers unterschiedlich lang sind. Das durchgeführte Experiment lieferte in Übereinstimmung mit der Speziellen Relativitätstheorie ein Nullresultat und bestätigte, dass neben der Längenkontraktion auch die Zeitdilatation angenommen werden muss. Nach diesem indirekten Nachweis erfolgte der erste direkte Nachweis der Zeitdilatation durch das Ives-Stilwell-Experiment. Aus der Kombination der Resultate dieser drei Experimente (dem Michelson-Morley-Experiment zur Messung der Abhängigkeit der Lichtgeschwindigkeit von der Beobachterorientierung, dem Kennedy-Thorndike-Experiment zur Messung der Abhängigkeit der Lichtgeschwindigkeit von der Beobachtergeschwindigkeit und dem Ives-Stilwell-Experiment zur Messung der Zeitdilatation) kann die Lorentz-Transformation abgeleitet werden.[2] Das Experiment wurde zuerst von Roy J. Kennedy und Edward M. Thorndike durchgeführt.
Moderne Kennedy-Thorndike-Experimente, mit denen dieselben Zusammenhänge zwischen Beobachtergeschwindigkeit und Lichtgeschwindigkeit bzw. zwischen Zeitdilatation und Längenkontraktion untersucht werden, werden bis heute mit deutlich größerer Genauigkeit mittels optischer Resonatoren und Lunar Laser Ranging durchgeführt und bestätigen das ursprüngliche Resultat. (vgl. Tests der speziellen Relativitätstheorie für weitere Experimente.)
Geschichte
Das Kennedy-Thorndike-Experiment ist eine Variante des Michelson-Morley-Experiments (1887). Mit letzterem sollte die Existenz einer Relativbewegung zwischen Erde und Äther (Ätherwind) festgestellt werden, doch das Ergebnis war negativ. Um diesen negativen Ausgang zu erklären, wurde von George Francis FitzGerald (1889) und Hendrik Antoon Lorentz (1892) die Existenz einer Längenkontraktion postuliert. Diese ursprüngliche Kontraktionshypothese wurde von Hendrik Antoon Lorentz aufgrund der Experimente von Rayleigh und Brace (1902, 1904) und des Trouton-Noble-Experiments (1903) durch die Hinzunahme der Zeitdilatation zur Lorentz-Transformation erweitert und mündete in der von Albert Einstein 1905 formulierten und bis heute gültigen Speziellen Relativitätstheorie. Dies wurde durch das Kennedy-Thorndike-Experiment (mit dem das Verhältnis zwischen Längenkontraktion und Zeitdilatation bestimmt wird) und dem Ives-Stilwell-Experiment (mit dem die Zeitdilatation direkt gemessen wird) bestätigt. Außer durch die spezielle Relativitätstheorie kann dieses Experiment auch durch einen vollständig mitgeführten Äther oder die Emissionstheorie erklärt werden, jedoch sind diese beiden Theorien bereits durch andere Experimente widerlegt worden und müssen nicht mehr berücksichtigt werden.
Das Experiment
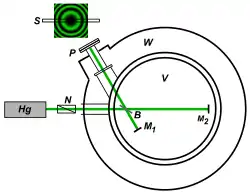
Um nachzuweisen, ob die Zeitdilatation neben der Längenkontraktion notwendig ist, änderten Kennedy und Thorndike (1932) das Michelson-Morley-Experiment insofern ab, indem sie einen Arm des Interferometers sehr viel kürzer als den anderen machten. Der Längenunterschied betrug 16 cm, eine größere Differenz schied aus experimentellen Gründen (die Kohärenz der Lichtquelle musste gesichert bleiben) aus. Außerdem drehten Kennedy und Thorndike das Interferometer nicht, sondern beobachteten mögliche Veränderungen in den Interferenzmustern aufgrund einer Änderung der Geschwindigkeit der Erde in den jeweiligen Armen des Interferometers (da sich die Richtung und der Betrag der Umlaufgeschwindigkeit um die Sonne ändert) über einige Monate. Gäbe es nur die Längenkontraktion, verschöben sich auch die Interferenzstreifen und das Ergebnis würde positiv ausfallen. Bei Änderung der Geschwindigkeit im längeren Arm ergäbe sich eine relative Verschiebung der Interferenzmuster aufgrund der Längenkontraktion. Nur wenn sich die Frequenz im Sinne der Zeitdilatation im selben Verhältnis änderte, wäre das Ergebnis negativ, das heißt, es würde keine Verschiebung beobachtet.
Um eine solche Verschiebung über mehrere Monate feststellen zu können, wurde das Interferometer extrem stabil gebaut und die Interferenzmuster wurden für spätere Vergleiche fotografiert. Die Tests wurden über mehrere Monate hinweg ausgeführt. Als keine signifikante Verschiebung festgestellt werden konnte (Obergrenze für Geschwindigkeitsänderungen von 10 ±10 km/s), schlossen die Experimentatoren, dass die ursprüngliche Kontraktionshypothese alleine nicht ausreicht und somit die Zeitdilatation tatsächlich existiert.
Theorie
Allgemeine Theorie des Experiments
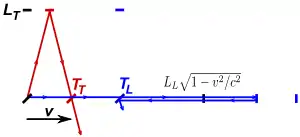
Wird ein Interferometer mit zwei senkrecht zueinander stehenden Armen der Längen LL und LT benutzt, wie beim Michelson-Morley-Experiment oder dem Kennedy-Thorndike-Experiment, dann ergeben sich folgende Streckendifferenzen (wobei ΔLA ist die ursprüngliche Differenz und vA die ursprüngliche Geschwindigkeit des Apparats; und ΔLB und vB nach einer Rotation bzw. einer Geschwindigkeitsänderung des Apparats aufgrund der Erdrotation oder der Umkreisung der Sonne):[3][4]
- .
ΔLA und ΔLB sind nicht gleich, woraus folgt, dass die Lichtgeschwindigkeit von der Orientierung des Apparats abhängt. Diese Differenz verschwindet allerdings wenn der Apparat eine Längenkontraktion in Bewegungsrichtung erfährt, also:
- .
Daraus ergibt sich aber, dass die Streckendifferenzen nur dann gleich sind, wenn die beiden Geschwindigkeiten vA und vB übereinstimmen. Unterschiedliche Geschwindigkeiten würden nämlich zu Unterschieden zwischen ΔLA und ΔLB führen. (Das betrifft nicht das Michelson-Morley-Experiment, denn hier ist von vornherein LL=LT und somit ΔLA=ΔLB=0. Deswegen wird mit diesem Test ausschließlich die Abhängigkeit der Lichtgeschwindigkeit von der Orientierung des Apparats gemessen, wofür die Längenkontraktion alleine ausreicht.) Hingegen beim Kennedy-Thorndike-Experiment sind die Interferometerarme unterschiedlich lang, weswegen mit diesem Test die Abhängigkeit der Lichtgeschwindigkeit von der Geschwindigkeit des Apparats überprüft werden kann.[2]
Gemäß obiger Formel ergibt sich der Streckenunterschied ΔLA−ΔLB und folglich die erwartete Streifenverschiebung (wobei λ die Wellenlänge ist), mit:[3]
oder wenn nur Größen zweiter Ordnung in v/c berücksichtigt werden:
Um diese Streifenverschiebung zu verhindern, muss die Frequenz und damit die Wellenlänge λ durch einen Faktor modifiziert werden, der genau der Zeitdilatation entspricht. Das bedeutet, sowohl Längenkontraktion als auch Zeitdilatation zusammen können die Resultate dieses und ähnlicher Experimente erklären.
Bedeutung für die Relativitätstheorie
Bereits 1905 zeigten Henri Poincaré und Albert Einstein, dass die Lorentz-Transformationen nur dann eine Gruppe bilden, wenn Längenkontraktion und Zeitdilatation die exakt relativistischen Werte haben. Die Gruppeneigenschaft ist wiederum eine notwendige Forderung des in der Erfahrung immer wieder bestätigten Relativitätsprinzips.
Nun glaubten Kennedy und Thorndike, dass es auch möglich sei, die Lorentz-Transformation nur aus den Ergebnissen des Michelson-Morley-Experiments und des Kennedy-Thorndike-Experiments herzuleiten. Das ist streng genommen nicht korrekt, da Längenkontraktion und Zeitdilatation in ihrer exakt relativistischen Gestalt zwar ausreichend, aber nicht notwendig sind um die Experimente zu erklären. Dies folgt daraus, dass die Längenkontraktion in Bewegungsrichtung der Körper nur ein Spezialfall der möglichen Erklärungen für das Michelson-Morley-Experiment sind. Allgemein muss nur angenommen werden, dass die Dimensionen bewegter Körper in longitudinaler und transversaler Richtung zueinander im Verhältnis des Lorentz-Faktors stehen – das beinhaltet unendlich viele Kombinationsmöglichkeiten von Längenverkürzungen und -dehnungen. Das beeinflusst auch die Rolle der Zeitdilatation im Kennedy-Thorndike-Experiment, da deren Wert in der Analyse des Experiments vom Wert der Längenkontraktion abhängt. Deswegen ist es notwendig, dass ein drittes Experiment berücksichtigt wird, das Ives-Stilwell-Experiment, um die Lorentz-Transformation exakt abzuleiten.[2]
Etwas genauer: Howard P. Robertson und andere[2][5] zeigten auf, dass folgendes Schema (vgl. Robertson-Mansouri-Sexl-Testheorie) zur Analyse der Experimente verwendet werden kann: α entspricht Zeitveränderungen, β Längenänderungen in Bewegungsrichtung und δ Längenänderungen senkrecht zur Bewegungsrichtung. Das Michelson-Morley-Experiment testet die Kombination von β und δ und das Kennedy-Thorndike-Experiment die Kombination von α und β. Somit hängt α von β ab, das wiederum von δ abhängt. Da nur die genannten Kombinationen dieser Ausdrücke durch diese beiden Experimente bestimmt werden können, nicht jedoch ihre individuellen Werte, ist es notwendig, einen dieser Ausdrücke direkt experimentell zu bestimmen. Das wurde mittels des Ives-Stilwell-Experiments erreicht, mit dem α in Übereinstimmung mit der relativistischen Zeitdilatation gemessen wurde. Wird dieser Wert von α mit dem Kennedy-Thorndike-Nullresultat kombiniert, ergibt sich für β notwendigerweise der Wert der relativistischen Längenkontraktion. Wird wiederum dieser Wert von β mit dem Michelson-Morley-Nullresultat kombiniert, ergibt sich, dass δ gleich Null sein muss. Dadurch sind experimentell die exakten Eigenschaften der Lorentz-Transformation gegeben, wie sie sich auch theoretisch aus den Forderungen der Gruppentheorie ergeben.
Moderne Experimente
Resonator-Experimente
Experimente vom Kennedy-Thorndike-Typ (sowie vom Michelson-Morley-Typ) werden bis heute in unterschiedlichen Variationen durchgeführt, und zwar unter Benutzung von Laser, Maser oder optischen Resonatoren. Anisotropien im Sinne einer Abhängigkeit von der Geschwindigkeit des Beobachters, und somit Tests des Zusammenhangs zwischen Längenkontraktion und Zeitdilatation im Sinne der Robertson-Mansouri-Sexl-Testheorie (RMS), wurden mit erheblich vergrößerter Präzision ausgeschlossen. Zum Vergleich: Im Rahmen von RMS erreichte das ursprüngliche Experiment eine Genauigkeit von ~10−2.[5]
| Autor | Jahr | Beschreibung | Maximale Geschwindigkeits- abhängigkeit |
|---|---|---|---|
| Hils and Hall[6] | 1990 | Es werden die Frequenzen eines optischen Fabry-Pérot-Resonators mit denen eines Lasers verglichen, der zu einer I2-Linie stabilisiert wurde. | |
| Braxmaier et al.[7] | 2002 | Die Frequenzen eines kryogenischen optischen Resonators mit einer I2-Linie verglichen, wobei zwei Nd:YAG-Laser benutzt wurden. | |
| Wolf et al.[8] | 2003 | Die Frequenz eines kryogenischen Mikrowellen-Oszillators wird mit einem Wasserstoffmaser vergleichen. Daten zwischen 2001 und 2002 wurden analysiert. | |
| Wolf et al.[9] | 2004 | Siehe Wolf et al. (2003). Daten zwischen 2002 und 2003 wurden analysiert. | |
| Tobar et al.[10] | 2009 | Siehe Wolf et al. (2003). Daten zwischen 2002 und 2008 wurden analysiert. |
Lunar Laser Ranging
Neben diesen terrestrischen Varianten führten Müller und Soffel (1995)[11] und Müller et al. (1999)[12] eine Art Kennedy-Thorndike-Experiment mit Lunar Laser Ranging, also anhand von Entfernungsmessungen Erde-Mond, durch. Eine etwaige Abhängigkeit der Lichtgeschwindigkeit von der Geschwindigkeit des Beobachters relativ zu einem bevorzugten Bezugssystems müsste im Laufe des Jahres zu Veränderungen der Laufzeit und somit zu Variationen in der gemessenen Entfernung Erde-Mond führen. Um dies auszugleichen müssen (wie in allen anderen Kennedy-Thorndike-Experimenten) sowohl Längenkontraktion als auch Zeitdilatation die exakt relativistischen Werte annehmen. Da die Zeitdilatation experimentell bereits sehr genau nachgewiesen wurde, hätte ein positives Ergebnis neben einer Abhängigkeit der Lichtgeschwindigkeit vom Beobachter auch eine Veränderlichkeit der Längenkontraktion bedeutet. Das Ergebnis war negativ, mit einer maximalen Geschwindigkeitsabhängigkeit von ∼10−5,[12] was vergleichbar ist mit den terrestrischen Experimenten von Hils und Hall (1990).
Einzelbelege
- R. J. Kennedy, E. M. Thorndike: Experimental Establishment of the Relativity of Time. In: Physical Review. 42, Nr. 3, 1932, S. 400–418. bibcode:1932PhRv...42..400K. doi:10.1103/PhysRev.42.400.
- H. P. Robertson: Postulate versus Observation in the Special Theory of Relativity. In: Reviews of Modern Physics. 21, Nr. 3, 1949, S. 378–382. doi:10.1103/RevModPhys.21.378.
- Albert Shadowitz: Special relativity, Reprint of 1968 edition. Auflage, Courier Dover Publications, 1988, ISBN 0-486-65743-4, S. 161.
- Robert Resnick: Introduction to Special Relativity. Wiley, 1968.
- R. Mansouri, R. U. Sexl: A test theory of special relativity: III. Second-order tests. In: General. Relat. Gravit.. 8, Nr. 10, 1977, S. 809–814. bibcode:1977GReGr...8..809M. doi:10.1007/BF00759585.
- Dieter Hils, J. L. Hall: Improved Kennedy-Thorndike experiment to test special relativity. In: Phys. Rev. Lett.. 64, Nr. 15, 1990, S. 1697–1700. bibcode:1990PhRvL..64.1697H. doi:10.1103/PhysRevLett.64.1697. PMID 10041466.
- C. Braxmaier et al.: Tests of Relativity Using a Cryogenic Optical Resonator. In: Phys. Rev. Lett.. 88, Nr. 1, 2002, S. 010401. bibcode:2002PhRvL..88a0401B. doi:10.1103/PhysRevLett.88.010401. PMID 11800924.
- P. Wolf et al.: Tests of Lorentz Invariance using a Microwave Resonator. In: Physical Review Letters. 90, Nr. 6, 2003, S. 060402. arxiv:gr-qc/0210049. bibcode:2003PhRvL..90f0402W. doi:10.1103/PhysRevLett.90.060402. PMID 12633279.
- P. Wolf et al.: Whispering Gallery Resonators and Tests of Lorentz Invariance. In: General Relativity and Gravitation. 36, Nr. 10, 2004, S. 2351–2372. arxiv:gr-qc/0401017. bibcode:2004GReGr..36.2351W. doi:10.1023/B:GERG.0000046188.87741.51.
- M. E. Tobar et al.: Testing local Lorentz and position invariance and variation of fundamental constants by searching the derivative of the comparison frequency between a cryogenic sapphire oscillator and hydrogen maser. In: Physical Review D. 81, Nr. 2, 2010, S. 022003. arxiv:0912.2803. bibcode:2010PhRvD..81b2003T. doi:10.1103/PhysRevD.81.022003.
- J. Müller, M. H. Soffel: A Kennedy-Thorndike experiment using LLR data. In: Physics Letters A. 198, 1995, S. 71–73. doi:10.1016/0375-9601(94)01001-B.
- J. Müller et al.: Improved Determination of Relativistic Quantities from LLR. (PDF) In: Proceedings of the 11th International Workshop on Laser Ranging Instrumentation. 10, 1999, S. 216–222.