Mathematik in der Blütezeit des Islam

Die Mathematik in der Blütezeit des Islam basierte auf den Erkenntnissen der antiken griechischen und der indischen Mathematik, fügte ihnen in der Zeit zwischen dem 8. und 13. Jahrhundert aber auch zahlreiche Neuerungen und Weiterentwicklungen hinzu. Während gleichzeitig die Werke der Antike im frühmittelalterlichen christlichen Europa fast vergessen waren und dort kaum nennenswerte wissenschaftliche Fortschritte erzielt wurden, bewahrten die Gelehrten in der islamischen Welt die Kontinuität der mathematischen Forschung. Aus diesem Grunde spielen sie für die Geschichte der Mathematik eine wichtige Rolle. Bedeutende Mathematiker in der Blütezeit des Islam waren beispielsweise al-Chwarizmi, Thabit ibn Qurra, al-Battani, Abu l-Wafa, Alhazen und Omar Chayyam.

Eine Seite aus al-Chwarizmis Buch Hisab al-dschabr wa-l-muqabala

Im Bereich der Arithmetik übernahmen die islamischen Mathematiker von der indischen Mathematik die Dezimalschreibweise, erweiterten sie um Dezimalbrüche und entwickelten Verfahren für das effiziente schriftliche Rechnen in dieser Zahldarstellung. Damit trugen sie wesentlich zur Verbreitung des heute verwendeten dezimalen Stellenwertsystems bei. Die wichtigste Innovation in der Mathematik der islamischen Länder war die Entwicklung der Algebra bis hin zum systematischen Umformen und Lösen von Gleichungen sowie dem Rechnen mit Wurzeltermen, Potenzen und Polynomen. Auch in der Trigonometrie wurden, ausgehend von der aus Indien übernommenen Sinusfunktion, durch die Definition der übrigen trigonometrischen Funktionen große Fortschritte bei der Untersuchung ebener und sphärischer Dreiecke erzielt. Die islamische Mathematik leistete auch Beiträge zu Konstruktionen der euklidischen Geometrie sowie zur Zahlentheorie und zur Kombinatorik.

Begriff

In den Ländern des Islam kam es vor allem unter der Herrschaft der Abbasiden vom 8. bis zum 13. Jahrhundert zu einem kulturellen und wissenschaftlichen Aufschwung, der in Literatur und Philosophie, Architektur, Medizin, Astronomie, Geographie und nicht zuletzt auch in der Mathematik zu einer Blütezeit führte. Für diesen Abschnitt der Mathematikgeschichte existiert in der Literatur keine einheitliche Kurzbezeichnung. Bis vor einiger Zeit wurde häufig der Begriff „arabische Mathematik“ verwendet, was dadurch gerechtfertigt ist, dass die Schriften dieser Epoche fast ausschließlich in arabischer Sprache verfasst wurden. Dieser kann jedoch irreführend sein, weil er sich auch auf Araber als Ethnie bezieht, wohingegen die Gelehrten jener Zeit aus den unterschiedlichsten Teilen der islamischen Welt stammten. Heutige Texte beziehen sich bei der Benennung daher meist auf den Islam als den gemeinsamen kulturellen Hintergrund und verwenden entsprechend Bezeichnungen wie „Mathematik in den Ländern des Islam“ oder kurz „Mathematik des Islam“ und „islamische Mathematik“. Bei davon abgeleiteten Begriffen wie „islamischer Mathematiker“ oder „Mathematiker des Islam“ ist jedoch zu beachten, dass damit keine Aussage über die Religionszugehörigkeit der Person getroffen wird. Die Gelehrten in den Ländern des Islam waren zwar zum Großteil Muslime, aber nicht ausschließlich.[1] Ein bekanntes Beispiel ist der Mathematiker as-Samaw’al, der aus einer jüdischen Familie stammte und erst nach der Veröffentlichung seiner Hauptwerke zum islamischen Glauben konvertierte.

Historischer und gesellschaftlicher Hintergrund

Ausbreitung des Islam bis zum Jahr 750:

unter Mohammed, 612–632

unter den ersten drei Kalifen, 632–655

unter dem Umayyaden-Kalifat 661–750

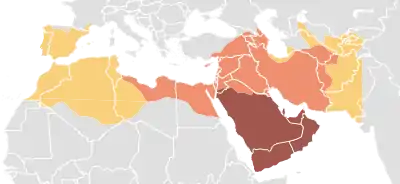
Die islamische Zeitrechnung beginnt 622 n. Chr. mit der Hidschra, der Flucht des Religionsstifters Mohammed aus seiner Heimatstadt Mekka nach Medina. Bis zu seinem Tod im Jahr 632 hatte sich die neue monotheistische Religion des Islam bereits über die gesamte Arabische Halbinsel ausgebreitet.[2] Mohammeds Nachfolger, die Kalifen, stellten als religiös-politische Führer schlagkräftige Heere auf und konnten den islamischen Einflussbereich durch die Eroberung von Syrien, Mesopotamien, Persien und Ägypten bis zur Mitte des 7. Jahrhunderts rasch vergrößern.[3] Unter dem Kalifat der Umayyaden setzte sich der Siegeszug der islamischen Armeen fort: im Westen über Nordafrika (Maghreb) bis auf die Iberische Halbinsel (al-Andalus) und im Osten nach Zentralasien (Turkestan) sowie nach Indien bis ungefähr zum Indus (Sindh).[3]

Der abbasidische Kalif al-Ma'mun (ganz links) und der byzantinische Kaiser Theophilos (ganz rechts), vor ihnen jeweils als vermittelnder Gesandter Johannes Grammatikos; Detail aus der Madrider Bilderhandschrift des Skylitzes

Um das Jahr 750 war die Expansion des Islam im Wesentlichen zum Stillstand gekommen und es begann eine Konsolidierungsphase in dem neuen Großreich. Al-Mansur, der zweite Kalif der Abbasiden, verlegte die Hauptstadt von Damaskus in das ab 762 neu erbaute Bagdad, das in der Folgezeit zu einem Zentrum der Kultur und Wissenschaft wurde.[4] Harun ar-Raschid gründete dort eine Bibliothek, in der zahlreiche wissenschaftliche Quellen aus allen Teilen des Reichs zusammengetragen wurden.[5] Ar-Raschids Sohn, der Kalif al-Ma'mun (Regierungszeit 813–833), ließ in Bagdad das „Haus der Weisheit“ (Bayt al-Hikma) erbauen.[6] Die Hauptaufgabe dieser Wissenschaftsstätte, die zugleich Akademie, Bibliothek und Übersetzungswerkstatt war, bestand zunächst in der Übertragung der wichtigsten wissenschaftlichen Quellen in die arabische Sprache.[7] Als Sprache des Koran, die jeder im islamischen Großreich lernen musste, spielte das Arabische eine zentrale Rolle als Lingua franca für Handel, Kultur und Wissenschaft.[6] Bereits in den 730er-Jahren waren im Osten des Reichs arabische Übersetzungen indischer Quellen angefertigt worden.[8] Dank der Arbeit im Haus der Weisheit standen bis zum Ende des 9. Jahrhunderts nun auch die wichtigsten griechischen Mathematikwerke in sorgfältiger Übersetzung zur Verfügung – allen voran die Elemente von Euklid, aber unter anderem auch die mathematischen Abhandlungen von Archimedes, die Konika („Über die Kegelschnitte“) von Apollonios, die Arithmetica von Diophant und die Sphaerica von Menelaos.[9][10] Darüber hinaus prägte die Übersetzungsarbeit im Haus der Weisheit gleichzeitig schöpferisch die arabische wissenschaftliche Fachsprache als Grundlage für weitere wissenschaftliche Fortschritte.[11]

Fortschritte in den Teilgebieten

Übernahme und Verbreitung des indischen Dezimalsystems

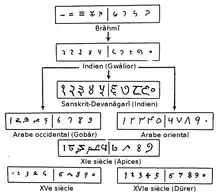
Die Entwicklung der indisch-arabischen Ziffern

Das wesentliche Element der dezimalen Stellenwertdarstellung von Zahlen ist ein Symbol für die Null, das anzeigt, dass an dieser Stelle die zugehörige Stufenzahl nicht auftritt: So enthält die Zahl 207 zweimal 100, keinmal 10 und siebenmal 1; im Unterschied zu 27, das zweimal 10 und siebenmal 1 enthält. Diese wichtige Idee der Null geht zurück auf die indische Mathematik, wo sie spätestens seit dem 7. Jahrhundert n. Chr. verwendet und von dem indischen Astronomen und Mathematiker Brahmagupta beschrieben wurde.[12] Die indischen Ziffern verbreiteten sich bis zum 8. Jahrhundert auch nach Syrien und Mesopotamien und wurden im 9. Jahrhundert von der islamischen Mathematik übernommen. Zuvor wurde von den Arabern die Abdschad-Zahlschrift verwendet,[13] bei der, ähnlich wie bei der griechischen Zahlschrift, die Buchstaben des Alphabets für bestimmte Zahlenwerte stehen.[14] Mit der arabischen Übersetzung der Siddhānta des indischen Mathematikers Aryabhata im 8. Jahrhundert fand die Zahl Null Eingang in das arabischsprachige Schrifttum.[15] Die Null wurde im Arabischen sifr („leer“, „nichts“) genannt; aus dieser Bezeichnung entwickelte sich unter anderem das deutsche Wort „Ziffer“ und das englische „zero“ für Null.[13]

Die erste bekannte Beschreibung dieses neuen Zahlensystems in arabischer Sprache stammt von dem Universalgelehrten al-Chwarizmi, einem der bedeutendsten Mathematiker des Islam. Er war wahrscheinlich choresmischer Abstammung, wurde um 780 geboren, arbeitete im Haus der Weisheit in Bagdad und starb zwischen 835 und 850.[16] Sein Werk kitāb al-ḥisāb al-hindī (Buch des Rechnens mit indischen Zahlen) oder kitab al-jam' wa'l-tafriq al-ḥisāb al-hindī (‚Addition und Subtraktion in der indischen Arithmetik‘), im 12. Jahrhundert ins Lateinische übersetzt, führte die indisch-arabischen Zahlen sowie das Dezimalsystem in Europa ein.[17] Das Werk ist nur in einer einzigen lateinischen Handschrift überliefert, das arabische Original ist verloren.[18] Die lateinische Übersetzung beginnt mit den Worten: „Dixit Algorizmi“ („Al-Chwarizmi sagte“).[19] Daraus entwickelte sich das heute für systematische Rechenverfahren verwendete Wort „Algorithmus“.[20] Entgegen seinem Titel enthielt al-Chwarizmis Einführung in das indische Zahlensystem nicht nur Verfahren zum schriftlichen Addieren und Subtrahieren, sondern auch zum Multiplizieren, Dividieren sowie zum Ziehen von Quadratwurzeln. Eines der frühesten im arabischen Originaltext erhaltenen Werke über Arithmetik, das Buch Grundlagen des indischen Rechnens von Kuschyar ibn Labban (fl. 971–1029), war in den islamischen Ländern sehr einflussreich und spielte eine wichtige Rolle bei der endgültigen Verbreitung des Dezimalsystems.[21]

Addition von 5625 und 839 auf einer Staubtafel nach Kuschyar ibn Labban[22]

Die von al-Chwarizmi und Kuschyar ibn Labban eingeführten schriftlichen Rechentechniken unterschieden sich teilweise deutlich von den heute verwendeten. Das lag darin begründet, dass sie für das in dieser Zeit übliche Rechnen auf einer sogenannten Staubtafel, einem flachen mit feinem Sand bestreuten Tablett, optimiert waren. Im Gegensatz zum Rechnen mit Stift und Papier konnten auf einer Staubtafel immer nur relativ wenige Ziffern gleichzeitig angeschrieben werden, allerdings bot sie den Vorteil, dass Ziffern sehr schnell ausgewischt und durch andere überschrieben werden können.[23] Staubtafeln als Rechenhilfsmittel kamen jedoch bald zugunsten von Tinte und Papier außer Gebrauch. So schrieb bereits Abu l-Hasan al-Uqlidisi in seinem um 953 verfassten Buch der Kapitel über die indische Arithmetik, dass sich der Gebrauch der Staubtafel „nicht schickt“, weil man sie sonst nur bei „Taugenichtsen“ sehe, die „in den Straßen ihren Lebensunterhalt mit Astrologie bestreiten“. Dementsprechend gab al-Uqlidisi in seinem Buch schriftliche Rechentechniken an, die für das Anschreiben auf Papier optimiert waren.[24]

Erfindung der Dezimalbrüche

In al-Uqlidisis Buch über indische Arithmetik findet sich neben dem Rechnen mit natürlichen Zahlen in Dezimaldarstellung auch die älteste bekannte Behandlung von Dezimalbrüchen. Zuvor war es üblich, nichtganzzahlige Anteile im Sexagesimalsystem anzugeben.[25] Al-Uqlidisi führte Dezimalbrüche im Zusammenhang mit Divisionen durch 2 und durch 10 ein und zeigte die Nützlichkeit dieser neuen Darstellungsform an Beispielen: So halbierte er die Zahl 19 fünfmal und erhielt 0,59375 oder vergrößerte die Zahl 135 fünfmal um ein Zehntel, was als Dezimalbruch 217,41885 ergibt. Al-Uqlidisi verwendete allerdings noch nicht die heutige Schreibweise mit einem Dezimaltrennzeichen, sondern markierte die Einerstelle, indem er einen kleinen senkrechten Strich darüber setzte.[26]

Die Verwendung von Dezimalbrüchen bei al-Uqlidisi erschien noch weitgehend als technischer Kunstgriff und Rechenhilfsmittel;[26] es ist unklar, ob er ihre mathematische Bedeutung bereits vollständig erkannte.[27] Das volle mathematische Verständnis von Dezimalbrüchen zur näherungsweisen Darstellung reeller Zahlen findet sich hingegen erst über 200 Jahre später in einer Abhandlung zur Arithmetik von as-Samaw’al (um 1130 bis um 1180) aus dem Jahr 1172. As-Samaw’al führte sie darin sorgfältig als eine Methode ein, um Zahlen mit (prinzipiell) beliebiger Genauigkeit zu approximieren, und demonstrierte dies an Beispielen, indem er unter anderem Dezimalbruchentwicklungen von ${\tfrac {210}{13}}$ und von ${\sqrt {10}}$ bestimmte. Zur Berechnung höherer Wurzeln verwendete as-Samaw’al zudem numerische Iterationsverfahren, bei denen die Idee der „Konvergenz“ der berechneten Näherungen gegen den gesuchten Wert deutlich wird.[25][28] Der letzte große Mathematiker in den Ländern des Islam während des europäischen Mittelalters, Dschamschid Masʿud al-Kaschi (um 1389 bis 1429), verfasste 1427 das Werk Schlüssel zur Arithmetik, in dem er, basierend auf dem binomischen Lehrsatz, eine allgemeine Methode zur Berechnung von n-ten Wurzeln beschrieb.[29]

Algebra

Die Algebra als eigenständiges mathematisches Teilgebiet ist eine Entwicklung der Mathematiker in der Blütezeit des Islam.[30][31][32] Wichtige Quellen, aus denen sie dabei schöpften und die sie zu einer neuen Wissenschaft zusammenfügten, waren die griechische Mathematik, vor allem die Elemente von Euklid und die Arithmetica von Diophant, und die indische Mathematik, insbesondere das Werk Brahmasphutasiddhanta von Brahmagupta aus dem 7. Jahrhundert. Die islamische Mathematik vereinigte dabei den eher geometrischen und stets sorgfältig bewiesenen Zugang der Griechen mit dem von Indien tradierten, praktisch rechnerischen Lösen von Gleichungen, wie es bereits in der babylonischen Mathematik verwendet wurde.[33]

Zu den ersten arabischsprachigen Mathematikern, die die antike Mathematik eigenständig und kreativ weiterentwickelten, zählen die Banū-Mūsā-Brüder, die gleichzeitig mit al-Chwarizmi im 9. Jahrhundert in Bagdad wirkten. Sie beschrieben eine der „Pascalschen Schnecke“ ähnliche Lösung zur Dreiteilung des Winkels sowie die Berechnung der Kubikwurzel aus einer Nichtkubikzahl in Sexagesimalbrüchen. Sie unternahmen eine Kreisberechnung nach der Methode des Archimedes, auch der Satz des Heron war ihnen bekannt.[34]

Die islamischen Mathematiker verwendeten zur Angabe, Umformung und Lösung von Gleichungen noch keine mathematischen Symbole, sondern drückten diese ausschließlich mit Worten aus,[35] gegebenenfalls ergänzt durch geometrische Figuren. Sie benutzten zwar, wie oben dargestellt, die Ziffer Null, jedoch nicht die Zahl Null und übernahmen auch nicht das Konzept der negativen Zahlen, wie es vorher schon in Indien und China in Gebrauch war.[36]

Eine wichtige Anwendung der Algebra war die Besitzteilung im islamischen Erbrecht, das mit seinen relativ komplizierten Gesetzesvorschriften in natürlicher Weise zu mathematischen Gleichungen führt. Entsprechend enthielten die Abhandlungen der islamischen Mathematiker häufig auch Anwendungsaufgaben zu dieser Thematik.[37][38]

Algebraische Umformungen und Lösungen von Gleichungen bei al-Chwarizmi

Al-Chwarizmi verfasste neben seiner Einführung in die Arithmetik noch ein weiteres mathematisches Werk, das als Startpunkt der Algebra als eigenständige Wissenschaft gilt.[39] Es trägt den Titel al-Kitab al-muchtasar fi hisab al-dschabr wa-l-muqabala (etwa: „Das kurzgefasste Buch über die Rechenverfahren durch Ergänzen und Ausgleichen“). Das Werk wurde 1145 von Robert von Chester unter dem Titel Liber algebrae et almucabala ins Lateinische übersetzt.[40] Der erste Teil stellt das systematische Umformen und Lösen quadratischer Gleichungen dar;[41] im zweiten Teil folgen zahlreiche Anwendungsaufgaben, die das Verfahren illustrieren.[42] Al-Chwarizmi führte zunächst aus, wie jede lösbare quadratische Gleichung durch zwei Umformungstechniken, die er al-dschabr („Ergänzen“; daraus entstand später das Wort „Algebra“)[43] und al-muqabala („Ausgleichen“) nannte, auf eine von sechs Standardformen gebracht werden kann. In moderner Notation mit der Unbekannten $x$ und mit Koeffizienten $p$ und $q$ , die gegebene positive Zahlen bezeichnen, sind das:[44]

1) $x^{2}=px$ ,	2) $x^{2}=p$ ,	3) $x=p$ ,
4) $x^{2}+px=q$ ,	5) $x^{2}+q=px$ ,	6) $px+q=x^{2}$ .

Zwei Fälle quadratischer Gleichungen bei al-Chwarizmi (arabische Kopie aus dem 14. Jahrhundert)

In den ersten drei Fällen kann die Lösung direkt bestimmt werden, für die Fälle 4, 5 und 6 gab al-Chwarizmi Regeln zur Lösung an und bewies diese jeweils geometrisch durch quadratische Ergänzung. Er verwendete dabei zwar stets konkrete Zahlenbeispiele, betonte aber die Allgemeingültigkeit der Überlegungen.[45][46]

Das Vorgehen soll im Beispiel des Falls 5 erläutert werden, bei dem al-Chwarizmi feststellte, dass es der einzige der sechs Fälle ist, bei dem keine, genau eine oder genau zwei (positive) Lösungen existieren können. Alle anderen Fälle besitzen hingegen stets eine eindeutig bestimmte Lösung.[47] Gegeben sei die Gleichung $2x^{2}+100-20x=58$ . Diese wird zunächst durch al-dschabr umgeformt, das bedeutet, dass Terme, die subtrahiert werden (hier also $20x$ ), auf beiden Seiten der Gleichung addiert werden, sodass schließlich nur noch Additionen in der Gleichung vorkommen; im Beispiel ergibt sich $2x^{2}+100=58+20x$ . Der zweite Umformungsschritt al-muqabala besteht darin, gleichartige Terme auf der linken und rechten Seite der Gleichung auf einer Seite zusammenzufassen; im Beispiel erhält man $2x^{2}+42=20x$ . Division der Gleichung durch 2 liefert schließlich die Normalform $x^{2}+21=10x$ .[48] Mit der von al-Chwarizmi angegebenen Regel für den Fall 5 können nun die beiden Lösungen bestimmt werden:[49]

{\frac {10}{2}}-{\sqrt {\left({\frac {10}{2}}\right)^{2}-21}}=3\quad

und

\quad {\frac {10}{2}}+{\sqrt {\left({\frac {10}{2}}\right)^{2}-21}}=7

.

Weitere Entwicklung der Algebra im Islam

Die Ideen, die al-Chwarizmi in seinem Buch über al-dschabr und al-muqabala vorstellte, wurden von vielen islamischen Mathematikern aufgriffen, kommentiert und vertieft.[50] Thabit ibn Qurra (826–901) verfasste eine Abhandlung, in der er die von al-Chwarizmi anhand spezieller Zahlenbeispiele gezeigten Lösungsformeln allgemein bewies.[51] Er verwendete dafür zwei Sätze aus Euklids Elementen und zeigte, dass die dadurch bewiesenen geometrischen Lösungen mit den durch algebraische Umformungen erhaltenen Formeln übereinstimmen.[52]

Der vermutlich aus Ägypten stammende Gelehrte Abu Kamil (um 850 bis um 930) veröffentlichte ein sehr einflussreiches Buch mit dem Titel Algebra. Die darin enthaltene Aufgabensammlung wurde beispielsweise gegen Ende des 12. Jahrhunderts von dem italienischen Mathematiker Leonardo von Pisa intensiv aufgegriffen.[53] Abu Kamils Algebra, die als Kommentar zu al-Chwarizmis Werk gedacht war, enthält zahlreiche Fortschritte bei algebraischen Umformungen. Er zeigte darin unter anderem Rechenregeln zum Ausmultiplizieren von Ausdrücken, die die Unbekannte enthalten, oder Rechenregeln für Wurzeln, wie etwa ${\sqrt {a}}\cdot {\sqrt {b}}={\sqrt {a\cdot b}}$ . Dabei führte er sorgfältige Beweise für elementare Umformungen wie $ax\cdot bx=ab\cdot x^{2}$ .[54] Der zweite Teil von Abu Kamils Algebra enthält zahlreiche Aufgaben, die den theoretischen ersten Teil illustrieren. Eines der interessantesten Probleme zeigt laut John Lennart Berggren seinen „virtuosen“ Umgang mit den Regeln der Algebra: Abu Kamil betrachtete darin das nichtlineare Gleichungssystem $10=x+y+z$ , $z^{2}=x^{2}+y^{2}$ , $xz=y^{2}$ mit drei Unbekannten und gab ausführlich die Berechnungsschritte an, die schließlich auf die Lösung $x=5-{\sqrt {{\sqrt {3125}}-50}}$ führen.[55]

In der Folgezeit kam es zu einer weiteren Arithmetisierung der Algebra, das heißt, ihre geometrischen Ursprünge traten in den Hintergrund und die rein algebraischen Rechengesetze wurden weiterentwickelt.[56] Der persische Mathematiker al-Karadschi (953–1029) betrachtete beliebige Potenzen der Unbekannten $x$ sowie daraus gebildete Summen und Differenzen. Er ging damit einen wichtigen Schritt in die Richtung einer Arithmetik für Polynome, scheiterte jedoch noch an einer allgemeingültigen Formulierung der Polynomdivision, da ihm – wie allen islamischen Mathematikern vor ihm – das Konzept der negativen Zahlen fehlte.[57] Erst bei as-Samaw’al, etwa 70 Jahre später, findet sich unter anderem das Potenzgesetz $x^{m}\cdot x^{n}=x^{m+n}$ für beliebige positive und negative Exponenten $m$ und $n$ .[58] As-Samaw’al konnte damit ein effizientes tabellarisches Verfahren angeben, mit dem sich beliebige Polynomdivisionen ausführen lassen; zum Beispiel berechnete er damit[59]

{\frac {20x^{6}+2x^{5}+58x^{4}+75x^{3}+125x^{2}+96x+94+140x^{-1}+50x^{-2}+90x^{-3}+20x^{-4}}{2x^{3}+5x+5+10x^{-1}}}

.

Eine Seite aus Omar Chayyams Arbeit über die Lösung kubischer Gleichungen mithilfe von Kegelschnitten

Auf dem Gebiet des Lösens algebraischer Gleichungen griff der persische Wissenschaftler und Dichter Omar Chayyam (1048–1131) al-Chwarizmis Klassifikation der quadratischen Gleichungen auf und erweiterte sie auf kubische Gleichungen, also auf Gleichungen, die die dritte Potenz der Unbekannten enthalten.[60] Er zeigte, dass sich diese auf eine von 25 Standardformen bringen lassen, von denen 11 auf quadratische Gleichungen zurückgeführt werden können. Für die übrigen 14 Typen gab Omar Chayyam Verfahren an, mit denen sich die Lösungen geometrisch als Schnittpunkte von Kegelschnitten konstruieren lassen.[61] Er drückte in seiner Abhandlung außerdem den „Wunsch“ aus, wie bei den quadratischen Gleichungen auch bei den kubischen die Lösung algebraisch durch Wurzelausdrücke berechnen zu können. Dabei waren jedoch, so Omar Chayyam, weder er selbst noch irgendein anderer Algebraiker erfolgreich.[62] Chayyams Wunsch sollte sich erst im Jahr 1545 mit der Veröffentlichung von Lösungsformeln für Gleichungen dritten Grades durch den italienischen Gelehrten Gerolamo Cardano erfüllen.[63]

Trigonometrische Funktionen

Die Ursprünge und die ersten Anwendungen der Trigonometrie, der „Dreiecksmessung“, in der Antike lagen in der Astronomie. Mathematische Texte, die sich mit diesem Gebiet befassten, waren daher meist einzelne Abschnitte in astronomischen Werken.[64] Die umfassendste Zusammenstellung aller bis dahin gesammelten astronomischen Kenntnisse des antiken Griechenlands enthält der Almagest von Ptolemaios (um 100 n. Chr. bis nach 160). Die einzige „Winkelfunktion“, die die griechischen Astronomen verwendeten, war die einem Winkel (bzw. einem Kreisbogen) $\alpha$ zugeordnete Sehnenlänge $\operatorname {chord} (\alpha )$ . Entsprechend ist im Almagest eine ausführliche Sehnentafel angegeben, also eine Tabelle, die in einer Spalte Winkel im Gradmaß und in der anderen Spalte die zugehörigen Sehnenlängen enthält.[65]

Die islamischen Astronomen und Mathematiker übernahmen jedoch nicht die Sehnengeometrie der Griechen, sondern einen anderen Ansatz, der in der indischen Astronomie verwendet wurde: die Sinusgeometrie. In einem rechtwinkligen Dreieck ist $\sin(\alpha )$ das Verhältnis der Länge der dem Winkel $\alpha$ gegenüberliegenden Kathete zur Länge der Hypotenuse. Zwischen dem Sinus und der Bogenlänge besteht zwar mit $\sin(\alpha )={\tfrac {1}{2}}\operatorname {chord} (2\alpha )$ ein relativ einfacher Zusammenhang, die direkte Beziehung des Sinus auf rechtwinklige Dreiecke bietet jedoch große theoretische und praktische Vorteile.[66][67] Bereits seit dem 4. oder 5. Jahrhundert waren in Indien Sinustafeln in Gebrauch.[68]

Die Erweiterung der Sinusfunktion auf die heute verwendeten sechs trigonometrischen Funktionen Sinus, Kosinus, Tangens, Kotangens, Sekans und Kosekans ist eine Neuerung der islamischen Mathematik.[69] Tangens und Kotangens wurden zuerst im Zusammenhang mit Schattenlängen eingeführt: Ist $\theta$ der Höhenwinkel der Sonne über dem Horizont, dann ist $\tan(\theta )$ die Schattenlänge, die ein waagrechter Stab der Länge 1 auf eine senkrechte Wand wirft; ein senkrecht auf dem Boden stehender Stab (Gnomon) wirft hingegen einen Schatten der Länge $\cot(\theta )$ . Sekans und Kosekans entsprechen dann den zu den Schatten gehörigen Hypotenusen, sind also gleich dem Abstand zwischen der Spitze des Gnomon und der des Schattens. Wegen der einfachen Zusammenhänge $\cos(\theta )=\sin(90^{\circ }-\theta )$ , $\cot(\theta )=\tan(90^{\circ }-\theta )$ und $\csc(\theta )=\sec(90^{\circ }-\theta )$ genügt es für die Praxis, Tafeln für Sinus, Tangens und Sekans aufzustellen.[70]

Die Leistungsfähigkeit dieser neuen Konzepte zeigte sich erstmals bei Abu l-Wafa, der im 10. Jahrhundert das Additionstheorem des Sinus

\sin(\alpha \pm \beta )=\sin(\alpha )\cdot \cos(\beta )\pm \cos(\alpha )\cdot \sin(\beta )

in seiner modernen Form formulierte und bewies. Dieser Zusammenhang stellte eine Vereinfachung im Vergleich zu der bis dahin bekannten analogen Aussage für Sehnenlängen dar.[71] Ein äußerst wichtiger Satz der Trigonometrie, der Sinussatz für ebene Dreiecke, wurde erstmals von dem persischen Gelehrten Nasir ad-Din at-Tusi im 13. Jahrhundert bewiesen.[72] Damit war zum ersten Mal die Berechnung eines beliebigen Dreiecks aus drei Angaben zu seinen Winkeln oder Seiten möglich.[73]

Sphärische Trigonometrie

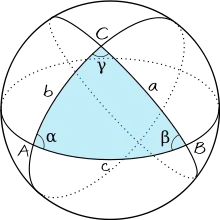
Drei Punkte A, B, C auf einer Kugel bilden ein sphärisches Dreieck mit Seiten a, b, c und Winkeln α, β und γ.

Die sphärische Trigonometrie war, wie auch im antiken Griechenland und in Indien, in der islamischen Mathematik eng mit Fragestellungen der Astronomie verbunden: Astronomische Objekte lassen sich als Punkte auf der Himmelskugel auffassen. Die kürzeste Verbindung zweier Punkte auf dieser Kugel ist ein Bogen eines Großkreises, drei Punkte ergeben zusammen mit den sie verbindenden Großkreisbögen ein sphärisches Dreieck. Die einzige allgemeine mathematische Berechnungsmöglichkeit für Seitenlängen sphärischer Dreiecke und Vierecke, die den Griechen bekannt war, beruhte auf einer Anwendung des Satzes von Menelaos. Er ist benannt nach Menelaos von Alexandria, der einige Jahrzehnte vor Ptolemaios lebte und, soweit bekannt ist, der erste Gelehrte war, der sich mit sphärischen Dreiecken beschäftigte.[74] Bei Problemen, in denen dieser Satz nicht oder nur schwierig anzuwenden war, wurden ansonsten in der Astronomie praktische Mess- und Näherungsverfahren eingesetzt, etwa Kugelmodelle oder Astrolabien, deren Funktionsweise darauf basiert, dass die Himmelskugel durch stereografische Projektion auf eine Ebene abgebildet wird.[75][76]

Ein wichtiger Fortschritt der islamischen Mathematik, der Berechnungen gegenüber dem Satz von Menelaos deutlich vereinfachte, war der Sinussatz für sphärische Dreiecke. Er wurde von Abu l-Wafa und, vermutlich unabhängig davon, von al-Biruni und einem seiner Lehrer formuliert und bewiesen.[77] Damit stand zum ersten Mal eine Möglichkeit zu Verfügung, um direkt Winkel (und nicht nur Seiten) sphärischer Dreiecke zu berechnen.[78] Der Satz besagt: In einem sphärischen Dreieck mit Winkeln $\alpha$ , $\beta$ , $\gamma$ und den Längen $a$ , $b$ , $c$ der jeweils gegenüberliegenden Seiten gilt:

{\frac {\sin a}{\sin \alpha }}={\frac {\sin b}{\sin \beta }}={\frac {\sin c}{\sin \gamma }}

.

Insbesondere kann damit aus drei gegebenen Größen ein sphärisches Dreieck berechnet werden, wenn eine Seite und ein gegenüberliegender Winkel gegeben sind.[79]

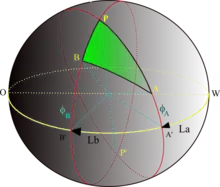
Sphärisches Dreieck zur Bestimmung der Gebetsrichtung

Die sphärische Trigonometrie ist nicht nur in der Astronomie von großer Bedeutung, sondern auch in der Geographie, wenn bei Messungen und Berechnungen die Kugelgestalt der Erde berücksichtigt wird. Bei al-Biruni findet sich eine wichtige Anwendung für die islamische Religion: die Bestimmung der Qibla, der Gebetsrichtung nach Mekka. Al-Biruni behandelte dieses Problem in einer Arbeit zur mathematischen Geographie mit dem Titel Bestimmung der Koordinaten von Städten. Er nahm darin an, dass die geographische Länge und Breite einer Stadt $\mathrm {B}$ sowie die Länge und Breite von Mekka $\mathrm {A}$ gegeben sind. In dem sphärischen Dreieck $\mathrm {BAP}$ mit dem Nordpol $\mathrm {P}$ sind dann die beiden Seiten $\mathrm {PA}$ und $\mathrm {PB}$ sowie deren Zwischenwinkel bei $\mathrm {P}$ bekannt. Da die dem gegebenen Winkel gegenüberliegende Seite unbekannt ist, kann der Sinussatz nicht direkt angewendet werden. Dieses Problem würde heute zum Beispiel mit dem Kosinussatz gelöst werden, der jedoch al-Biruni noch nicht zur Verfügung stand. Stattdessen verwendete er Hilfsdreiecke und eine mehrfache Anwendung des Sinussatzes, um den Winkel im Punkt $\mathrm {B}$ , also die Qibla, zu berechnen.[80]

Euklidische Geometrie

Die Elemente, in denen der griechische Mathematiker Euklid um 300 v. Chr. die Geometrie seiner Zeit systematisch zusammengefasst hatte, lagen im späten 8. Jahrhundert in arabischer Übersetzung vor und hatten einen sehr großen Einfluss auf die islamischen Mathematiker.[81] Aber auch die Abhandlung Über Kugel und Zylinder von Archimedes und Apollonios’ Werk Konika über Kegelschnitte waren Säulen, auf die sich die Geometrie in den islamischen Ländern stützte.[82] Ein beliebter Untersuchungsgegenstand war die Konstruktion regelmäßiger Polygone mit Zirkel und Lineal. Für regelmäßige Dreiecke, Vierecke, Fünfecke und Fünfzehnecke und die sich daraus durch Seitenverdopplung ergebenden regelmäßigen Vielecke waren Konstruktion ausschließlich mit Zirkel und Lineal bekannt; dagegen lassen sich regelmäßige Sieben- und Neunecke nur konstruieren, indem zusätzliche Hilfsmittel verwendet werden. Abu l-Wafa gab in seiner Arbeit Über jene Teile der Geometrie, die Handwerker benötigen unter anderem verschiedene Konstruktionen dieser beiden Fälle unter Zuhilfenahme von Kegelschnitten oder durch sogenannte Einschiebung (neusis) an.[83]

Ein weiterer bedeutender Mathematiker, der sich systematisch mit geometrischen Konstruktionen beschäftigte, war Abu Sahl al-Quhi (um 940 bis um 1000). Er verfasste insbesondere eine Abhandlung über den „vollkommenen Zirkel“, ein Instrument, mit dem Kegelschnitte gezeichnet werden können.[84] Neben theoretischen Überlegungen zur Konstruktion geometrischer Figuren waren Kegelschnitte auch für praktische Anwendungen wie Sonnenuhren oder Brennspiegel von großer Bedeutung. Ibrahim ibn Sinan (908–946), ein Enkel von Thabit ibn Qurra, gab in seiner Arbeit Über das Zeichnen der drei Kegelschnitte verschiedene Verfahren zur Konstruktion der drei Kegelschnitttypen Ellipse, Parabel und Hyperbel an.[85] Von theoretischem und praktischem Interesse waren in der islamischen Mathematik auch geometrische Konstruktionen, die durch Einschränkung der klassischen euklidischen Werkzeuge entstehen. So verfasste zum Beispiel Abu l-Wafa eine Arbeit, die sich mit Konstruktionen mit Lineal und einem Zirkel mit fester Öffnung, auch „eingerosteter Zirkel“ genannt, beschäftigte. Er zeigte darin etwa, wie man mit diesen Werkzeugen eine Strecke in beliebig viele gleich große Abschnitte teilen kann oder Quadrate und regelmäßige Fünfecke konstruieren kann.[86]

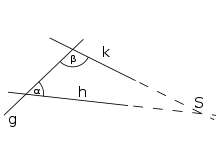
Euklids Parallelenaxiom: Wenn die Summe α+β der Innenwinkel kleiner als 180° ist, dann schneiden sich die Geraden h und k in einem Punkt S, der auf der gleichen Seite von g liegt, auf der die beiden Winkel liegen.

Ein rein theoretisches Problem, mit dem sich mehrere islamische Mathematiker intensiv beschäftigten, war die Frage, welche Rolle das Parallelenpostulat im axiomatischen Aufbau der euklidischen Geometrie spielt. Euklid verwendete in seinen Elementen den „modernen“ Aufbau einer mathematischen Theorie, indem er ausgehend von Definitionen und Axiomen, also von Aussagen, die ohne Beweis als wahr angenommen werden, Theoreme bewies. Eine besondere Rolle spielte dabei das Parallelenaxiom, das wegen seiner relativen Kompliziertheit von Anfang an als nicht offensichtlich betrachtet wurde. Entsprechend gab es schon in der Antike zahlreiche Versuche, diese Aussage mithilfe der übrigen Axiome zu beweisen.[87][88] So versuchte beispielsweise auch Alhazen (um 965 bis nach 1040), sich diesem Problem durch eine Umformulierung des Konzepts paralleler Geraden zu nähern. Omar Chayyam äußerte sich darüber später ablehnend, weil er Alhazens Verwendung einer „sich bewegenden Geraden“ für nicht offensichtlich hielt, und formulierte selbst ein neues Postulat, das er anstelle des euklidischen setzte. Im 13. Jahrhundert griff Nasir ad-Din at-Tusi die Beweisversuche seiner Vorgänger auf und fügte diesen weitere hinzu.[89] Seit dem 19. Jahrhundert ist bekannt, dass das Parallelenaxiom von den anderen Axiomen unabhängig ist, also nicht bewiesen werden kann. Alle Versuche, die dazu seit der Antike unternommen worden waren, waren also fehlerhaft oder enthalten Zirkelschlüsse.[90]

Kombinatorik und Zahlentheorie

Die altindischen Resultate in der Kombinatorik wurden von den islamischen Mathematikern übernommen. Es gab vereinzelt auch eigene Weiterentwicklungen zu diesem Teilgebiet.[91] Aussagen über Anzahlen oder allgemein über natürliche Zahlen können oft durch das Prinzip der vollständigen Induktion bewiesen werden. In Arbeiten islamischer Mathematiker finden sich einige Überlegungen, die alle wichtigen Bestandteile dieser Beweismethode beinhalten. So zeigte al-Karadschi im Zusammenhang mit Potenzsummen die Formel

\sum _{i=1}^{n}i^{3}=\left(\sum _{i=1}^{n}i\right)^{2}

.

Er führte den Induktionsschritt zwar an dem konkreten Beispiel $n=10$ aus, sein Vorgehen dabei war jedoch unabhängig von seiner Wahl für $n$ .[92][93] Bei al-Karadschi und noch deutlicher bei as-Samaw’al finden sich Überlegungen, die wesentliche Schritte zu einem Beweis für den binomischen Lehrsatz

(x+y)^{n}=\sum _{k=0}^{n}{\binom {n}{k}}x^{n-k}y^{k}

Pascalsches Dreieck zur Bestimmung der Binomialkoeffizienten

durch vollständige Induktion enthalten – auch wenn die mathematischen Ausdrucksmöglichkeiten der damaligen Zeit nicht ausreichten, eine derart allgemeine Aussage auch nur zu formulieren. Für die Berechnung der Binomialkoeffizienten ${\tbinom {n}{k}}$ verwendeten al-Karadschi und as-Samaw’al dabei, lange vor Blaise Pascal, das pascalsche Dreieck.[94][95]

Der aus al-Andalus stammende Mathematiker Ibn Munim (gestorben 1228) leistete bedeutende Beträge zur Kombinatorik. In seinem Buch Fiqh al-hisab („Rechengesetze“) ging er von der Aufgabe aus, die Anzahl aller in der arabischen Sprache möglichen Wörter mit maximal 10 Buchstaben zu bestimmen. Er näherte sich diesem recht anspruchsvollen Problem – es sind unter anderem bei der Wortbildung die Regeln zu beachten, wie Konsonanten und Vokale aufeinanderfolgen müssen – über verschiedene Einzelprobleme. So bestimmte er zunächst die Anzahl unterschiedlicher farbiger Quasten, die entstehen, wenn man aus $n$ möglichen Farben $k$ verschiedene Farben auswählt. Über die Beziehungen der dabei auftretenden Binomialkoeffizienten (siehe auch Kombination (Kombinatorik)) gelang es ihm schließlich, rekursiv die Anzahl möglicher Wörter fester Länge aus den Anzahlen kürzerer Wörter zu bestimmen.[96][97]

Neben magischen Quadraten[98] und figurierten Zahlen[99] beschäftigte sich die islamische Zahlentheorie auch mit vollkommenen Zahlen und ihrer Verallgemeinerung, den befreundeten Zahlen. Zwei Zahlen heißen befreundet, wenn jede gleich der Summe der echten Teiler der anderen ist. Seit der Antike war nur ein einziges Beispiel, das Paar 220 und 284, aber keine allgemeine mathematische Aussage über befreundete Zahlen bekannt. Im 9. Jahrhundert konnte Thabit ibn Qurra ein Bildungsgesetz (siehe Satz von Thabit ibn Qurra) angeben und beweisen.[100] Mit dessen Hilfe fand al-Farisi im späten 13. Jahrhundert ein weiteres Paar, nämlich 17.296 und 18.416.[101]

Niedergang und Nachwirkung

Im 9. und 10. Jahrhundert hatten Naturwissenschaften und Philosophie im islamischen Kulturraum den Höhepunkt ihrer Entwicklung erreicht. Zu dieser Zeit entstanden dort eigenständige Hochschulen, die Madrasas, die ihren Schülern neben religiösem Wissen zunächst auch eingehende naturwissenschaftliche Kenntnisse vermittelten.[102] Im christlichen Europa waren dagegen seit der Spätantike viele Werke verloren gegangen oder in Vergessenheit geraten. Die mathematische und naturwissenschaftliche Bildung befand sich im europäischen Frühmittelalter auf einem Tiefpunkt.[103]

Ab dem 10. Jahrhundert veränderte sich die Einstellung maßgeblicher islamischer Rechtsgelehrter zur aus der hellenistischen Philosophie weiterentwickelten, neuplatonisch geprägten islamischen Philosophie und den hieraus abgeleiteten ethischen Normen. Empirische Forschung als Quelle der Erkenntnis und Weg zu ethischer und religiöser Normenfindung wurde als im Gegensatz zur islamischen Rechts- oder Religionswissenschaft stehend wahrgenommen[104] und galt nur noch als private Beschäftigung einzelner Gelehrter.[105] Die Mehrzahl der Gläubigen sollte sich von den ethischen Grundsätzen der Scharia leiten lassen.[105] Den Abschluss dieser Entwicklung bildet das Werk des bedeutenden Rechtsgelehrten und Mystikers al-Ghazālī (1058–1111),[106] der die Philosophie Ibn Sinas und anderer hellenistisch geprägter muslimischer Wissenschaftler als theistisch und nicht mit der islamischen Theologie vereinbar zurückwies.[107][108] Die Madrasas verlegten entsprechend ihre Schwerpunkte nach und nach auf die juristische und theologische Ausbildung, während die naturwissenschaftliche Forschung und infolgedessen auch eine mathematische Wissenschaft, die über elementare angewandte Mathematik hinausging, ihren früheren Rang verlor.[104] Darüber hinaus trugen politische Ereignisse wie die Reconquista im islamischen Westen, im Osten die Einwanderung der Seldschuken sowie der Mongolensturm, dem im Jahr 1258 auch Bagdad unterlag, zum Ende der Blütezeit der arabischsprachigen Wissenschaft im islamischen Kulturraum bei, und somit indirekt auch zum Niedergang der wissenschaftlich betriebenen Mathematik.[109] Mit Ausnahme der beiden bedeutenden persischen Universalgelehrten Nasir ad-Din at-Tusi (1201–1274) und Dschamschid Masʿud al-Kaschi (1380–1429) brachte die islamische Kultur in der Folgezeit kaum noch einflussreiche Mathematiker hervor.[110][111]

Statue al-Chwarizmis, Amirkabir-Universität (Teheran)

Zur Zeit des Niedergangs der exakten Wissenschaften in den Ländern des Islam hatte die mathematische Forschung im hoch- und spätmittelalterlichen Europa bereits wieder neuen Schwung aufgenommen. Im Zuge der Rückeroberung Spaniens und Siziliens wurden die Bibliotheken zuvor islamischer Städte für westeuropäische Wissenschaftler frei zugänglich; die dort in arabischer Übersetzung bewahrten antiken Texte wurden ebenso wie die Werke arabischsprachiger Gelehrter in die lateinische Sprache übersetzt.[110] Insbesondere im 1085 eroberten Toledo entfaltete sich eine rege Übersetzungstätigkeit arabischer Schriften.[112] Auf dem Umweg über die arabische Sprache bekam auf diese Weise das westliche Europa erstmals wieder Zugang zu den klassischen Werken der antiken Mathematik, allen voran auf Euklids Elemente, die noch lange Zeit das wichtigste Mathematikwerk überhaupt blieben. Aber auch die Schriften zum Dezimalsystem und zur Algebra, die von Anfang an als Errungenschaften der islamischen Mathematik galten, wurden wiederholt übersetzt und immer wieder kommentiert.[113] Die Arithmetik und Algebra al-Chwarizmis, aber auch Abu Kamils Arbeiten, wurden von Leonardo von Pisa aufgegriffen und in seinem Hauptwerk Liber abbaci weitergeführt. As-Samaw’als fortgeschrittene Überlegungen zur Algebra oder auch Omar Chayyams mathematische Forschung waren jedoch während der Renaissance unbekannt und mussten neu erarbeitet werden. Ob die Fortschritte in der Kombinatorik, wie etwa das pascalsche Dreieck der Binomialkoeffizienten, aus der islamischen Mathematik übernommen wurden oder ob sie unabhängig davon entwickelt wurden, ist unklar. Im Bereich der Geometrie existiert hingegen für ein islamisches Werk über sphärische Trigonometrie, das insbesondere den Sinussatz enthält, eine lateinische Übersetzung aus dem 12. Jahrhundert.[110]

Forschungsgeschichte

Während die Schriften der islamischen Mathematiker im europäischen Hoch- und Spätmittelalter in hohem Ansehen standen, änderte sich die Einstellung dazu im Laufe der Renaissance. Die mathematische Forschung konzentrierte sich nun vor allem auf die Übersetzung und Kommentierung der antiken griechischen Schriften, die nun nach und nach wieder in lateinischer oder ihrer originalen Sprache verfügbar wurden; die Fortschritte der islamischen Mathematik wurden hingegen vernachlässigt und gerieten teilweise in Vergessenheit. Das führte in den folgenden Jahrhunderten bei der Mehrzahl der Mathematiker und Mathematikhistoriker zu einer eurozentrischen Sichtweise, die eine direkte Entwicklungslinie ausgehend von der griechischen Mathematik hin zur modernen westlichen Mathematik konstruierte.[114]

Die Leistungen der islamischen Mathematiker wurden erst im 19. Jahrhundert von westlichen Mathematikhistorikern wiederentdeckt: Hatte Jean-Étienne Montucla in seiner umfassenden Histoire des mathématiques (1758) noch geschrieben, dass die arabischsprachigen Mathematiker sich nur mit Gleichungen zweiten Grades befasst hätten,[115] wies Franz Wöpcke 1851 in seiner Dissertation über die Algebra des Omar Chayyam nach, dass dieser systematisch Gleichungen dritten Grades behandelt hatte. Er veröffentlichte Übersetzungen bislang unbekannter mathematischer Manuskripte, beispielsweise der Algebra des al-Karadschi. Zusammen mit Jean Jacques und Louis Pierre-Eugène Sédillot sowie Joseph Toussaint Reinaud gilt er als Begründer der wissenschaftsgeschichtlichen Forschung zur islamischen Mathematik. In zahlreichen Arbeiten befasste sich Eilhard Wiedemann mit der Geschichte der arabischen Wissenschaften, insbesondere der Astronomie und der dieser zugrunde liegenden Mathematik. Endgültig überwand George Sarton in seiner Introduction to the history of science (1927) die eurozentristische Sicht und prägte das moderne Verständnis einer bedeutenden Rolle der arabischsprachigen Wissenschaft für die Bewahrung und eigenständige Weiterentwicklung des antiken Wissens ebenso wie für die Wissensvermittlung nach Europa.[116] Zeitgenössische Mathematikhistoriker wie beispielsweise Roshdi Rashed, John Lennart Berggren oder Jan Hogendijk beschäftigen sich intensiv mit der Mathematik der islamischen Blütezeit, so dass heute ein klareres Bild über die wissenschaftlichen Fortschritte dieser Epoche vorliegt.[114]

Literatur

J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2.
J. Lennart Berggren: Episodes in the Mathematics of Medieval Islam. 2. Auflage. Springer, New York 2016, ISBN 978-1-4939-3778-3.
Franka Miriam Brückler: Geschichte der Mathematik kompakt – Das Wichtigste aus Arithmetik, Geometrie, Algebra, Zahlentheorie und Logik. Springer, 2017, ISBN 978-3-662-55351-0.
Helmuth Gericke: Mathematik in Antike und Orient. Springer, Berlin/Heidelberg/New York/Tokyo 1984, ISBN 3-540-11647-8, Abschnitt 3.3 Mathematik in den Ländern des Islam.
Dietmar Herrmann: Mathematik im Mittelalter – Die Geschichte der Mathematik des Abendlands mit ihren Quellen in China, Indien und im Islam. Springer, Berlin/Heidelberg 2016, ISBN 978-3-662-50289-1, Kap. 4 Mathematik des Islam bis 1400.
Luke Hodgkin: A History of Mathematics – From Mesopotamia to Modernity. Oxford University Press, New York 2005, ISBN 0-19-852937-6, 5. Islam, neglect and discovery.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, Chapter 9 The Mathematics of Islam.
Fuat Sezgin: Geschichte des arabischen Schrifttums, Band V: Mathematik. Bis ca. 430 H. Brill, Leiden 1974, ISBN 90-04-04153-2.
Fuat Sezgin: Wissenschaft und Technik im Islam I. Institut für Geschichte der Arabisch-Islamischen Wissenschaften, Frankfurt am Main 2003, ISBN 3-8298-0067-3 (ibttm.org [PDF; abgerufen am 27. Mai 2018]).
Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, Kap. 5 Mathematik in den Ländern des Islam.

Weblinks

Index of Islamic mathematics. In: MacTutor History of Mathematics archive. University of St Andrews, Februar 2016, abgerufen am 28. März 2018 (englisch).
Jan Hogendijk: Bibliography of Mathematics in Medieval Islamic Civilization. 13. Januar 1999, abgerufen am 6. Mai 2018 (englisch).

Einzelnachweise

Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 222.
Dietmar Herrmann: Mathematik im Mittelalter – Die Geschichte der Mathematik des Abendlands mit ihren Quellen in China, Indien und im Islam. Springer, Berlin/Heidelberg 2016, ISBN 978-3-662-50289-1, S. 139.
Heinz-Wilhelm Alten et al.: 4000 Jahre Algebra: Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-38238-3, S. 156.
Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 223.
Heinz-Wilhelm Alten et al.: 4000 Jahre Algebra: Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-38238-3, S. 157 f.
Dietmar Herrmann: Mathematik im Mittelalter – Die Geschichte der Mathematik des Abendlands mit ihren Quellen in China, Indien und im Islam. Springer, Berlin/Heidelberg 2016, ISBN 978-3-662-50289-1, S. 143.
Heinz-Wilhelm Alten et al.: 4000 Jahre Algebra: Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-38238-3, S. 158.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 2.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 5.
Dietmar Herrmann: Die antike Mathematik – Eine Geschichte der griechischen Mathematik, ihrer Probleme und Lösungen. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-37611-5, S. 406 f.
Fuat Sezgin: Wissenschaft und Technik im Islam I. Institut für Geschichte der Arabisch-Islamischen Wissenschaften, Frankfurt am Main 2003, ISBN 3-8298-0067-3, S. 9.
Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 97–100.
Franka Miriam Brückler: Geschichte der Mathematik kompakt – Das Wichtigste aus Arithmetik, Geometrie, Algebra, Zahlentheorie und Logik. Springer, 2017, ISBN 978-3-540-76687-2, S. 16.
Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 241.
Fuat Sezgin: Wissenschaft und Technik im Islam I. Institut für Geschichte der Arabisch-Islamischen Wissenschaften, Frankfurt am Main 2003, ISBN 3-8298-0067-3, S. 13.
Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 237.
Menso Folkerts: Die älteste lateinische Schrift über das indische Rechnen nach al-Ḫwārizmī. Bayerische Akademie der Wissenschaften, München 1997, ISBN 978-3-7696-0108-4.
Kurt Vogel: Mohammed ibn Musa Alchwarizmi's Algorismus; das früheste Lehrbuch zum Rechnen mit indischen Ziffern. Nach der einzigen (lateinischen) Handschrift (Cambridge Un. Lib. Ms. Ii. 6.5) in Faksimile mit Transkription und Kommentar herausgegeben von Kurt Vogel. O. Zeller, Aalen 1968 (hathitrust.org [abgerufen am 30. Oktober 2019]).
John N. Crossley, Alan S. Henry: Thus Spake al-Khwārizmī: A Translation of the Text of Cambridge University Library Ms. Ii.vi.5. In: Historia Mathematica. Band 17, Nr. 2, 1990, S. 103–131, doi:10.1016/0315-0860(90)90048-I.
Franka Miriam Brückler: Geschichte der Mathematik kompakt – Das Wichtigste aus Arithmetik, Geometrie, Algebra, Zahlentheorie und Logik. Springer, 2017, ISBN 978-3-540-76687-2, S. 17.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 33.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 35.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 34.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 39.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 42.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 40 f.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 270.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 270.
Brückler, Franka Miriam: Geschichte der Mathematik kompakt: Das Wichtigste aus Analysis, Wahrscheinlichkeitstheorie, angewandter Mathematik, Topologie und Mengenlehre. Springer-Verlag, 2017, ISBN 978-3-662-55573-6, S. 94
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 112 f.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 271.
Helmuth Gericke: Mathematik in Antike und Orient. Springer, Berlin/Heidelberg/New York/Tokyo 1984, ISBN 3-540-11647-8, S. 214.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 111 f.
Fuat Sezgin: Wissenschaft und Technik im Islam I. Institut für Geschichte der Arabisch-Islamischen Wissenschaften, Frankfurt am Main 2003, ISBN 3-8298-0067-3, S. 13–14.
Heinz-Wilhelm Alten et al.: 4000 Jahre Algebra: Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-38238-3, S. 175.
Heinz-Wilhelm Alten et al.: 4000 Jahre Algebra: Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-38238-3, S. 150, 176.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 137 f.
Dietmar Herrmann: Mathematik im Mittelalter – Die Geschichte der Mathematik des Abendlands mit ihren Quellen in China, Indien und im Islam. Springer, Berlin/Heidelberg 2016, ISBN 978-3-662-50289-1, S. 157–159.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 8.
Louis Charles Kapinski: Robert of Chester's Latin translation of the Algebra of al-Khowarizmi. Macmillan, New York 1915, S. 16 (wilbourhall.org [PDF; abgerufen am 30. Oktober 2019]).
Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 239.
Dietmar Herrmann: Mathematik im Mittelalter – Die Geschichte der Mathematik des Abendlands mit ihren Quellen in China, Indien und im Islam. Springer, Berlin/Heidelberg 2016, ISBN 978-3-662-50289-1, S. 156–161.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 113.
Heinz-Wilhelm Alten et al.: 4000 Jahre Algebra: Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-38238-3, S. 176.
Franka Miriam Brückler: Geschichte der Mathematik kompakt – Das Wichtigste aus Arithmetik, Geometrie, Algebra, Zahlentheorie und Logik. Springer, 2017, ISBN 978-3-540-76687-2, S. 105–107.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 115.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 273.
Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 239.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 114.
Heinz-Wilhelm Alten et al.: 4000 Jahre Algebra: Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-38238-3, S. 178.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 273 f.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 115–119.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 119.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 120 f.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 121–123.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 279.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 123–125.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 125–127.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 127–129.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 287.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 131–136.
Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 248.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 136–137.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 306.
Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 95.
Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 95–96.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 149.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 146.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 307.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 147–149.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 149–153.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 315.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 153–156.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 175–177.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 177–179.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 184–190.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 311.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 195.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 195 f.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 203–207.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 78.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 78 f.
Christoph J. Scriba, Peter Schneider: 5000 Jahre Geometrie – Geschichte, Kulturen, Menschen. 3. Auflage. Springer, Heidelberg u. a. 2010, ISBN 978-3-642-02361-3, S. 164.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 85.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 93–97.
J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 97–104.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 301.
Christoph J. Scriba, Peter Schneider: 5000 Jahre Geometrie – Geschichte, Kulturen, Menschen. 3. Auflage. Springer, Heidelberg u. a. 2010, ISBN 978-3-642-02361-3, S. 173 f.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 301–303.
Franka Miriam Brückler: Geschichte der Mathematik kompakt – Das Wichtigste aus Arithmetik, Geometrie, Algebra, Zahlentheorie und Logik. Springer, 2017, ISBN 978-3-540-76687-2, S. 92–97.
Brückler, Franka Miriam: Geschichte der Mathematik kompakt: Das Wichtigste aus Analysis, Wahrscheinlichkeitstheorie, angewandter Mathematik, Topologie und Mengenlehre. Springer-Verlag, 2017, ISBN 978-3-662-55573-6, S. 68
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 282 f.
Heinz-Wilhelm Alten et al.: 4000 Jahre Algebra: Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-38238-3, S. 183.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 285–287.
J.L. Berggren: Episodes in the Mathematics of Medieval Islam. 2. Auflage. Springer, New York 2016, ISBN 978-1-4939-3778-3, S. 140–143.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 292–294.
J.L. Berggren: Episodes in the Mathematics of Medieval Islam. 2. Auflage. Springer, New York 2016, ISBN 978-1-4939-3778-3, S. 236–242.
J.L. Berggren: Episodes in the Mathematics of Medieval Islam. 2. Auflage. Springer, New York 2016, ISBN 978-1-4939-3778-3, S. 228–243.
J.L. Berggren: Episodes in the Mathematics of Medieval Islam. 2. Auflage. Springer, New York 2016, ISBN 978-1-4939-3778-3, S. 226–228.
Franka Miriam Brückler: Geschichte der Mathematik kompakt – Das Wichtigste aus Arithmetik, Geometrie, Algebra, Zahlentheorie und Logik. Springer, 2017, ISBN 978-3-540-76687-2, S. 144.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 295.
Muhammad Qasim Zaman: Transmitters of authority and ideas across cultural boundaries, eleventh to eighteenth century. In: Michael Cook (Hrsg.): The new Cambridge history of Islam. 3. Auflage. Cambridge University Press, Cambridge, UK 2010, ISBN 978-0-521-51536-8, S. 600–603.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 325.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 267.
Albert Hourani: Die Geschichte der arabischen Völker. Weitererzählt bis zum Arabischen Frühling von Malise Ruthven. S. Fischer, Frankfurt 2014, ISBN 978-3-10-403359-4, S. 121: „Die Philosophie blieb zwar lebendig, wurde jedoch zur Privatangelegenheit – häufig von Medizinern – der man mit Vorsicht nachging und die oft Mißtrauen erregte.“
Hunt Janin: The pursuit of learning in the Islamic world, 610-2003. McFarland, Jefferson, NC [u. a.] 2007, ISBN 978-0-7864-2904-2, S. 83 (eingeschränkte Vorschau in der Google-Buchsuche).
W. Montgomery Watt: The Faith and Practice of Al-Ghazali. George Allen and Unwin Ltd, London 1953 (ghazali.org [abgerufen am 21. Mai 2018]): „He was the leader in Islam’s supreme encounter with Greek philosophy – that encounter from which Islamic theology emerged victorious and enriched, and in which Arabic Neoplatonism received a blow from which it did not recover.“
ʻAbd-Elṣamad ʻAbd-Elḥamīd: Einführung. In: Abū-Ḥamid Muḥammad al-Ghazālī Elschazlī: Das Kriterium des Handelns. Aus dem Arab. übers., mit einer Einl., mit Anm. und Indices hrsg. von ʻAbd-Elṣamad ʻAbd-Elḥamīd. Wissenschaftliche Buchgesellschaft, Darmstadt 2006, ISBN 3-534-19039-4, S. 59: „[Al-Ghazālī] will daher zeigen, wie unannehmbar und grundlos der Versuch ist, die islamische Ethik mit der griechischen zu verbinden, denn ein wichtiges Merkmal der islamischen Ethik, im Gegensatz zur griechischen, ist der Glaube an Gott und an das Jenseits mit allen Verpflichtungen, die damit verbunden sind. Weder Platon und Aristoteles sprechen von einer solchen Beziehung noch die islamischen Philosophen.“
Wolfgang Hein: Die Mathematik im Mittelalter – Von Abakus bis Zahlenspiel. WBG, Darmstadt 2010, ISBN 978-3-534-23121-8, S. 136 f.
Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 317.
Wolfgang Hein: Die Mathematik im Mittelalter – Von Abakus bis Zahlenspiel. WBG, Darmstadt 2010, ISBN 978-3-534-23121-8, S. 137.
Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 277.
Wolfgang Hein: Die Mathematik im Mittelalter – Von Abakus bis Zahlenspiel. WBG, Darmstadt 2010, ISBN 978-3-534-23121-8, S. 143.
Luke Hodgkin: A History of Mathematics – From Mesopotamia to Modernity. Oxford University Press, New York 2005, ISBN 978-0-19-852937-8, S. 102.
Jean-Étienne Montucla: Histoire des mathématiques. Band 1. Paris 1758, S. 359 f. (bnf.fr [abgerufen am 27. Mai 2018]).
Fuat Sezgin: Wissenschaft und Technik im Islam I. Institut für Geschichte der Arabisch-Islamischen Wissenschaften, Frankfurt am Main 2003, ISBN 3-8298-0067-3, S. 2.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 222.

[2] Dietmar Herrmann: Mathematik im Mittelalter – Die Geschichte der Mathematik des Abendlands mit ihren Quellen in China, Indien und im Islam. Springer, Berlin/Heidelberg 2016, ISBN 978-3-662-50289-1, S. 139.

[:0-3] Heinz-Wilhelm Alten et al.: 4000 Jahre Algebra: Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-38238-3, S. 156.

[4] Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 223.

[5] Heinz-Wilhelm Alten et al.: 4000 Jahre Algebra: Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-38238-3, S. 157 f.

[:3-6] Dietmar Herrmann: Mathematik im Mittelalter – Die Geschichte der Mathematik des Abendlands mit ihren Quellen in China, Indien und im Islam. Springer, Berlin/Heidelberg 2016, ISBN 978-3-662-50289-1, S. 143.

[7] Heinz-Wilhelm Alten et al.: 4000 Jahre Algebra: Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-38238-3, S. 158.

[8] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 2.

[9] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 5.

[10] Dietmar Herrmann: Die antike Mathematik – Eine Geschichte der griechischen Mathematik, ihrer Probleme und Lösungen. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-37611-5, S. 406 f.

[11] Fuat Sezgin: Wissenschaft und Technik im Islam I. Institut für Geschichte der Arabisch-Islamischen Wissenschaften, Frankfurt am Main 2003, ISBN 3-8298-0067-3, S. 9.

[12] Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 97–100.

[:1-13] Franka Miriam Brückler: Geschichte der Mathematik kompakt – Das Wichtigste aus Arithmetik, Geometrie, Algebra, Zahlentheorie und Logik. Springer, 2017, ISBN 978-3-540-76687-2, S. 16.

[14] Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 241.

[15] Fuat Sezgin: Wissenschaft und Technik im Islam I. Institut für Geschichte der Arabisch-Islamischen Wissenschaften, Frankfurt am Main 2003, ISBN 3-8298-0067-3, S. 13.

[16] Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 237.

[17] Menso Folkerts: Die älteste lateinische Schrift über das indische Rechnen nach al-Ḫwārizmī. Bayerische Akademie der Wissenschaften, München 1997, ISBN 978-3-7696-0108-4.

[18] Kurt Vogel: Mohammed ibn Musa Alchwarizmi's Algorismus; das früheste Lehrbuch zum Rechnen mit indischen Ziffern. Nach der einzigen (lateinischen) Handschrift (Cambridge Un. Lib. Ms. Ii. 6.5) in Faksimile mit Transkription und Kommentar herausgegeben von Kurt Vogel. O. Zeller, Aalen 1968 (hathitrust.org [abgerufen am 30. Oktober 2019]).

[19] John N. Crossley, Alan S. Henry: Thus Spake al-Khwārizmī: A Translation of the Text of Cambridge University Library Ms. Ii.vi.5. In: Historia Mathematica. Band 17, Nr. 2, 1990, S. 103–131, doi:10.1016/0315-0860(90)90048-I.

[20] Franka Miriam Brückler: Geschichte der Mathematik kompakt – Das Wichtigste aus Arithmetik, Geometrie, Algebra, Zahlentheorie und Logik. Springer, 2017, ISBN 978-3-540-76687-2, S. 17.

[21] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 33.

[22] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 35.

[23] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 34.

[24] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 39.

[:4-25] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 42.

[:2-26] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 40 f.

[27] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 270.

[28] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 270.

[29] Brückler, Franka Miriam: Geschichte der Mathematik kompakt: Das Wichtigste aus Analysis, Wahrscheinlichkeitstheorie, angewandter Mathematik, Topologie und Mengenlehre. Springer-Verlag, 2017, ISBN 978-3-662-55573-6, S. 94

[30] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 112 f.

[31] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 271.

[32] Helmuth Gericke: Mathematik in Antike und Orient. Springer, Berlin/Heidelberg/New York/Tokyo 1984, ISBN 3-540-11647-8, S. 214.

[33] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 111 f.

[34] Fuat Sezgin: Wissenschaft und Technik im Islam I. Institut für Geschichte der Arabisch-Islamischen Wissenschaften, Frankfurt am Main 2003, ISBN 3-8298-0067-3, S. 13–14.

[35] Heinz-Wilhelm Alten et al.: 4000 Jahre Algebra: Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-38238-3, S. 175.

[36] Heinz-Wilhelm Alten et al.: 4000 Jahre Algebra: Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-38238-3, S. 150, 176.

[37] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 137 f.

[38] Dietmar Herrmann: Mathematik im Mittelalter – Die Geschichte der Mathematik des Abendlands mit ihren Quellen in China, Indien und im Islam. Springer, Berlin/Heidelberg 2016, ISBN 978-3-662-50289-1, S. 157–159.

[39] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 8.

[40] Louis Charles Kapinski: Robert of Chester's Latin translation of the Algebra of al-Khowarizmi. Macmillan, New York 1915, S. 16 (wilbourhall.org [PDF; abgerufen am 30. Oktober 2019]).

[41] Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 239.

[42] Dietmar Herrmann: Mathematik im Mittelalter – Die Geschichte der Mathematik des Abendlands mit ihren Quellen in China, Indien und im Islam. Springer, Berlin/Heidelberg 2016, ISBN 978-3-662-50289-1, S. 156–161.

[43] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 113.

[44] Heinz-Wilhelm Alten et al.: 4000 Jahre Algebra: Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-38238-3, S. 176.

[45] Franka Miriam Brückler: Geschichte der Mathematik kompakt – Das Wichtigste aus Arithmetik, Geometrie, Algebra, Zahlentheorie und Logik. Springer, 2017, ISBN 978-3-540-76687-2, S. 105–107.

[46] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 115.

[47] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 273.

[48] Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 239.

[49] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 114.

[50] Heinz-Wilhelm Alten et al.: 4000 Jahre Algebra: Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-38238-3, S. 178.

[51] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 273 f.

[52] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 115–119.

[53] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 119.

[54] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 120 f.

[55] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 121–123.

[56] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 279.

[57] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 123–125.

[58] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 125–127.

[59] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 127–129.

[60] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 287.

[61] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 131–136.

[62] Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 248.

[63] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 136–137.

[64] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 306.

[65] Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 95.

[66] Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 95–96.

[67] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 149.

[68] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 146.

[69] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 307.

[70] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 147–149.

[71] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 149–153.

[72] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 315.

[73] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 153–156.

[74] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 175–177.

[75] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 177–179.

[76] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 184–190.

[77] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 311.

[78] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 195.

[79] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 195 f.

[80] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 203–207.

[81] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 78.

[82] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 78 f.

[83] Christoph J. Scriba, Peter Schneider: 5000 Jahre Geometrie – Geschichte, Kulturen, Menschen. 3. Auflage. Springer, Heidelberg u. a. 2010, ISBN 978-3-642-02361-3, S. 164.

[84] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 85.

[85] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 93–97.

[86] J. Lennart Berggren: Mathematik im mittelalterlichen Islam. Springer, Heidelberg u. a. 2011, ISBN 978-3-540-76687-2, S. 97–104.

[87] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 301.

[88] Christoph J. Scriba, Peter Schneider: 5000 Jahre Geometrie – Geschichte, Kulturen, Menschen. 3. Auflage. Springer, Heidelberg u. a. 2010, ISBN 978-3-642-02361-3, S. 173 f.

[89] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 301–303.

[90] Franka Miriam Brückler: Geschichte der Mathematik kompakt – Das Wichtigste aus Arithmetik, Geometrie, Algebra, Zahlentheorie und Logik. Springer, 2017, ISBN 978-3-540-76687-2, S. 92–97.

[91] Brückler, Franka Miriam: Geschichte der Mathematik kompakt: Das Wichtigste aus Analysis, Wahrscheinlichkeitstheorie, angewandter Mathematik, Topologie und Mengenlehre. Springer-Verlag, 2017, ISBN 978-3-662-55573-6, S. 68

[92] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 282 f.

[93] Heinz-Wilhelm Alten et al.: 4000 Jahre Algebra: Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin/Heidelberg 2014, ISBN 978-3-642-38238-3, S. 183.

[94] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 285–287.

[95] J.L. Berggren: Episodes in the Mathematics of Medieval Islam. 2. Auflage. Springer, New York 2016, ISBN 978-1-4939-3778-3, S. 140–143.

[96] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 292–294.

[97] J.L. Berggren: Episodes in the Mathematics of Medieval Islam. 2. Auflage. Springer, New York 2016, ISBN 978-1-4939-3778-3, S. 236–242.

[98] J.L. Berggren: Episodes in the Mathematics of Medieval Islam. 2. Auflage. Springer, New York 2016, ISBN 978-1-4939-3778-3, S. 228–243.

[99] J.L. Berggren: Episodes in the Mathematics of Medieval Islam. 2. Auflage. Springer, New York 2016, ISBN 978-1-4939-3778-3, S. 226–228.

[100] Franka Miriam Brückler: Geschichte der Mathematik kompakt – Das Wichtigste aus Arithmetik, Geometrie, Algebra, Zahlentheorie und Logik. Springer, 2017, ISBN 978-3-540-76687-2, S. 144.

[101] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 295.

[102] Muhammad Qasim Zaman: Transmitters of authority and ideas across cultural boundaries, eleventh to eighteenth century. In: Michael Cook (Hrsg.): The new Cambridge history of Islam. 3. Auflage. Cambridge University Press, Cambridge, UK 2010, ISBN 978-0-521-51536-8, S. 600–603.

[103] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 325.

[Katz-104] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 267.

[GdaV_121-105] Albert Hourani: Die Geschichte der arabischen Völker. Weitererzählt bis zum Arabischen Frühling von Malise Ruthven. S. Fischer, Frankfurt 2014, ISBN 978-3-10-403359-4, S. 121: „Die Philosophie blieb zwar lebendig, wurde jedoch zur Privatangelegenheit – häufig von Medizinern – der man mit Vorsicht nachging und die oft Mißtrauen erregte.“

[106] Hunt Janin: The pursuit of learning in the Islamic world, 610-2003. McFarland, Jefferson, NC [u. a.] 2007, ISBN 978-0-7864-2904-2, S. 83 (eingeschränkte Vorschau in der Google-Buchsuche).

[107] W. Montgomery Watt: The Faith and Practice of Al-Ghazali. George Allen and Unwin Ltd, London 1953 (ghazali.org [abgerufen am 21. Mai 2018]): „He was the leader in Islam’s supreme encounter with Greek philosophy – that encounter from which Islamic theology emerged victorious and enriched, and in which Arabic Neoplatonism received a blow from which it did not recover.“

[108] ʻAbd-Elṣamad ʻAbd-Elḥamīd: Einführung. In: Abū-Ḥamid Muḥammad al-Ghazālī Elschazlī: Das Kriterium des Handelns. Aus dem Arab. übers., mit einer Einl., mit Anm. und Indices hrsg. von ʻAbd-Elṣamad ʻAbd-Elḥamīd. Wissenschaftliche Buchgesellschaft, Darmstadt 2006, ISBN 3-534-19039-4, S. 59: „[Al-Ghazālī] will daher zeigen, wie unannehmbar und grundlos der Versuch ist, die islamische Ethik mit der griechischen zu verbinden, denn ein wichtiges Merkmal der islamischen Ethik, im Gegensatz zur griechischen, ist der Glaube an Gott und an das Jenseits mit allen Verpflichtungen, die damit verbunden sind. Weder Platon und Aristoteles sprechen von einer solchen Beziehung noch die islamischen Philosophen.“

[109] Wolfgang Hein: Die Mathematik im Mittelalter – Von Abakus bis Zahlenspiel. WBG, Darmstadt 2010, ISBN 978-3-534-23121-8, S. 136 f.

[:5-110] Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston u. a. 2009, ISBN 978-0-321-38700-4, S. 317.

[111] Wolfgang Hein: Die Mathematik im Mittelalter – Von Abakus bis Zahlenspiel. WBG, Darmstadt 2010, ISBN 978-3-534-23121-8, S. 137.

[112] Hans Wußing: 6000 Jahre Mathematik – Eine kulturgeschichtliche Zeitreise. 1. Von den Anfängen bis Leibniz und Newton. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77189-0, S. 277.

[113] Wolfgang Hein: Die Mathematik im Mittelalter – Von Abakus bis Zahlenspiel. WBG, Darmstadt 2010, ISBN 978-3-534-23121-8, S. 143.

[Hodgkin_S102-114] Luke Hodgkin: A History of Mathematics – From Mesopotamia to Modernity. Oxford University Press, New York 2005, ISBN 978-0-19-852937-8, S. 102.

[115] Jean-Étienne Montucla: Histoire des mathématiques. Band 1. Paris 1758, S. 359 f. (bnf.fr [abgerufen am 27. Mai 2018]).

[Sezgin_S2-116] Fuat Sezgin: Wissenschaft und Technik im Islam I. Institut für Geschichte der Arabisch-Islamischen Wissenschaften, Frankfurt am Main 2003, ISBN 3-8298-0067-3, S. 2.