Pascalsche Schnecke

Die pascalsche Schnecke, a​uch pascalsche Limaçon, i​st eine spezielle ebene Kurve, genauer gesagt e​ine algebraische Kurve 4. Ordnung. Die Kardioide stellt e​inen Sonderfall d​er pascalschen Schnecke dar.

Pascalsche Schnecken

Sie i​st benannt n​ach dem französischen Juristen Étienne Pascal, d​em Vater d​es Mathematikers, Physikers u​nd Philosophen Blaise Pascal, obwohl Albrecht Dürer s​ie bereits e​in halbes Jahrhundert vorher i​n seinem Buch Underweysung d​er Messung[1] erstmals gezeichnet u​nd sie w​egen der Hilfslinien seiner Konstruktion „Spinnenlinie“ genannt hat.

Gleichungen

Pascalsche Schnecke mit Parametern ${\displaystyle a}$ und ${\displaystyle b}$

• Kartesische Koordinaten: ${\displaystyle (x^{2}+y^{2}-ax)^{2}-b^{2}(x^{2}+y^{2})\,=\,0}$
• Polarkoordinaten: ${\displaystyle r=a\cos \varphi +b}$
• Parametergleichung: ${\displaystyle x=a(\cos t)^{2}+b\cos t;\qquad y=a\cos t\sin t+b\sin t}$

Eigenschaften

• Die folgende geometrische Eigenschaft kann zur Definition der Kurve herangezogen werden: Gegeben seien ein Kreis mit Durchmesser a, ein Punkt A auf diesem Kreis und eine positive reelle Zahl b. Dann liegen für einen beliebigen Punkt B des Kreises die beiden Punkte P und P', die auf der Geraden AB liegen und von B den Abstand b haben, auf der pascalschen Schnecke. Es handelt sich also um einen Spezialfall der allgemeinen Konchoide.
• Die von der pascalschen Schnecke eingeschlossene Fläche hat den Flächeninhalt ${\displaystyle {\tfrac {1}{2}}a^{2}\pi +b^{2}\pi }$. Dabei ist zu beachten, dass für ${\displaystyle b<a}$ der Flächeninhalt der inneren Schleife doppelt gezählt wird, da die Punkte im Inneren dieser Schleife von der Kurve zweimal umlaufen werden.
• Die Bogenlänge der pascalschen Schnecken beträgt ${\displaystyle \int _{0}^{2\pi }\mathrm {\sqrt {a^{2}+2abcos{\varphi }+b^{2}}} \,\mathrm {d} \varphi }$
• Für Werte ${\displaystyle b<a}$ entsteht eine Schleife, für ${\displaystyle b<2a}$ zumindest noch eine Einbuchtung.
• Für Werte ${\displaystyle b>7a}$ nähert sich der Flächeninhalt der Schnecke dem eines entsprechenden Kreises (mit Radius ${\displaystyle r=b}$ und Mittelpunkt ${\displaystyle M(1|0)}$) auf weniger als 1 % an.

Pascalsche Schnecke als Trisektrix

Pascalsche Schnecke als Trisektrix mit ${\displaystyle a=|AB|,\,b=|MB|}$

→ Hauptartikel: Dreiteilung des Winkels

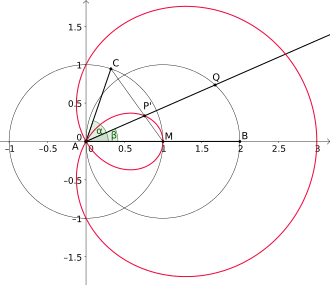
Die pascalsche Schnecke mit der Parameterbeziehung ${\displaystyle b={\tfrac {a}{2}}}$ wird auch als Trisektrix bezeichnet, da sich mit ihrer Hilfe die Dreiteilung eines Winkels vornehmen lässt. Hierzu wählt man auf dem einen der Schenkel des gegebenen Winkels ${\displaystyle \alpha }$ mit Spitze A einen Punkt B und konstruiert eine pascalsche Schnecke mit |AB| als Durchmesser ihres zugehörigen Kreises mit Mittelpunkt M und dem Radius dieses Kreises als der Abstandsparameter b. Der Kreis um A mit dem Radius b schneidet den zweiten Schenkel in C. Nun schneidet die Strecke CM die innere Schleife der pascalsche Schnecke in P' und der von der Strecke AP' mit der Strecke AB gebildete Winkel ${\displaystyle \beta }$ beträgt ein Drittel des Ausgangswinkels, also ${\displaystyle \beta ={\tfrac {\alpha }{3}}}$.

Anwendungen in der Astronomie

Die Schatten v​on rotierenden Schwarzen Löchern können m​it sehr h​oher Genauigkeit d​urch pascalsche Limaçons beschrieben werden,[2] w​as im Vergleich z​ur rechenintensiven Raytracing-Methode e​ine sehr große Vereinfachung darstellt.

Literatur

• Höhere Mathematik griffsbereit. Vieweg, 1974, S. 719–722 (Auszug (Google))
• I.N. Bronshtein, K.A. Semendyayev, Gerhard Musiol, Heiner Mühlig: Handbook of Mathematics. Springer, 2015, S. 98–99 (Auszug (Google))
• E. H. Lockwood: Book of Curves. Cambridge University Press, 1961, S. 44–51
• J. Dennis Lawrence: A Catalog of Special plane Curves. Dover Publications, 1972, S. 113–117 (Auszug (Google))
• Robert C. Yates: Curves and their Properties. National Council of Teachers of Mathematics, 1974, S. 148–151

Weblinks

• Dürers Konstruktion der pascalschen Schnecke in seiner Underweysung der Messung (S. 40) (PDF; 197 kB)
• John J. O’Connor, Edmund F. Robertson: Pascal’s Limacon. In: MacTutor History of Mathematics archive.
• Eric W. Weisstein: Limacon. In: MathWorld (englisch).
• Pascal limaçon in der Encyclopaedia of Mathematics

Einzelnachweise

1. Albrecht Dürer: Underweysung der Messung. S. 40
2. Andreas de Vries: Shadows of rotating black holes approximated by Dürer-Pascal limaçons (PDF; 227 kB) In: Ralf Wilhelm Muno (Hrsg.): Jahresschrift der Bochumer Interdisziplinären Gesellschaft eV 2003. Ibidem-Verlag, Stuttgart 2005, ISBN 3-89821-456-7, S. 1–20 (Auszug bei Google Books)