Apollonios von Perge
Apollonios von Perge (lateinisch Apollonius Pergaeus; * ca. 265 v. Chr. in Perge; † ca. 190 v. Chr. in Alexandria) war ein antiker griechischer Mathematiker, bekannt für sein Buch über Kegelschnitte. In der Astronomie trug er zur Theorie der Mond- und Planetenbewegung bei, die später Ptolemäus in sein Lehrbuch übernahm.
Leben
Über das Leben des Apollonios ist nur wenig bekannt und auch die genaue Lebenszeit wird in der Forschung diskutiert.[1] Apollonios studierte und wirkte wohl die meiste Zeit in Alexandria, insbesondere unter Ptolemaios III. und Ptolemaios IV. Er lebte offenbar auch irgendwann in Pergamon, wo sich wie in Alexandria eine große Bibliothek befand. Im ersten Buch seiner Konika erwähnt er die gemeinsame Zeit mit Eudemus in Pergamon, dem er die ersten drei Bücher seiner Schrift widmete. Im Proöm zum zweiten Buch der Konika erwähnt er einen gleichnamigen Sohn und den Epikureer Philonides, mit dem er vertraut war.[2]
Der Mondkrater Apollonius ist nach ihm benannt.
Werk
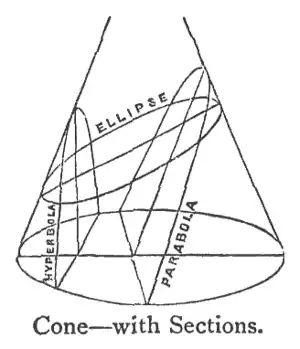
In seinem bedeutendsten Werk Konika („Über Kegelschnitte“) widmete er sich eingehenden Untersuchungen über Kegelschnitte, Grenzwertbestimmungen und Minimum-Maximum-Problemen. Die ersten drei Bücher sind dem Mathematiker Eudemus gewidmet, die anderen einem Attalos, der wohl nicht mit dem König identisch ist.[3] Er wies nach, dass die vier verschiedenen Kegelschnitte (Ellipse, Kreis, Parabel und Hyperbel), deren Namen und Definitionen er einführte, vom selben allgemeinen Kegeltypus stammen. Nach Zeuthen[4] war ihm bereits der Begriff der Koordinate bekannt. Nach Apollonios von Perge sind auch der Kreis des Apollonios, das Apollonische Problem und der Satz von Apollonios benannt.
In der Astronomie trug Apollonios zur Epizykeltheorie bei und zeigte deren Verbindung zur Exzenter-Theorie. Er erklärte damit die rückläufige Planetenbewegung und die unregelmäßige Bewegung des Mondes. Seine Berechnungsmethode der "Mittelpunktsgleichung"[5] wurde unter anderem von Hipparchos und Claudius Ptolemäus aufgegriffen und weiterentwickelt. Er soll auch eine verbesserte Sonnenuhr entwickelt haben mit Stundenlinien auf Kegelschnitten.

Lange galten die Bücher V bis VIII der Kegelschnitte als verloren (und verschiedene Mathematiker des 17. Jahrhunderts bemühten sich um eine Rekonstruktion, so Franciscus Maurolicus), bis sich in der Biblioteca Medicea Laurenziana in Florenz ein arabisches Manuskript (Übersetzung der Bücher V bis VII von Thabit ibn Qurra, Ausgabe der Banu Musa Brüder) mit den verloren geglaubten Büchern V bis VII fand, das von Giovanni Alfonso Borelli und Abraham Ecchellensis 1661 in Florenz als Übersetzung veröffentlicht wurde. Buch VIII gilt als verloren, es gab aber Rekonstruktionsversuche.
Buch 1 bis 4 behandeln als Einführung die elementare Theorie der Kegelschnitte, und das Material war größtenteils schon Euklid bekannt (wie Apollonios selbst schreibt), Buch 3 enthält aber auch neue Resultate. Von Buch 1 und 2 scheint es Vorversionen gegeben zu haben, die Apollonios zirkulieren ließ, auf denen einige der überlieferten Manuskripte beruhen. Buch 5 bis 7 enthalten völlig neues, sonst unbekanntes originäres Material von Apollonios, zum Beispiel zu Normalen an Kegelschnitte in Buch 5, die die spätere Konstruktion der Evolute an Kegelschnitte vorwegnehmen. In der Darstellung folgt Apollonios dem Stil von Euklids Elementen.
Pappos von Alexandria erwähnt die Titel weiterer Werke von Apollonios. Davon sind nur Ausschnitte bei Pappos, Proklos und anderen erhalten, abgesehen von einem arabischen Manuskript von De Rationis Sectione aus dem 10. Jahrhundert (weitere arabische Manuskripte sollen nach Ibn al-Nadim existiert haben, sind aber nicht erhalten). Pappos erwähnt noch De spatii sectione (Schnitt einer Fläche), De sectione determinata, De Tactionibus (Über Berührungen, Apollonisches Problem)[6], De Inclinationibus (Neigungen), De locis planis (Ebene Örter)[7], jeweils in zwei Büchern. Claudius Ptolemäus überlieferte zwei Lehrsätze aus einem verlorenen astronomischen Buch von Apollonios.
Weitere Bücher von Apollonios sind nur dem Titel nach bekannt: Hypsikles erwähnt ein Werk, in dem Apollonios die einer Kugel eingeschriebenen Dodekaeder und Ikosaeder vergleicht, Marinos erwähnt in einem Euklid-Kommentar ein allgemeines Werk von Apollonios über Grundlagen der Mathematik (Bedeutung von Axiomen, Definitionen u. a.), nach Proklos schrieb er ein Buch über irrationale Zahlen und über die Helix auf einem Zylinder. Er soll auch ein Buch über Brennspiegel geschrieben haben und nach Eutokios in einem Buch eine bessere Näherung an als Archimedes gegeben haben.
Von Eutokios stammt ein Kommentar zu den ersten vier Büchern der Kegelschnitte.
Ausgaben und Übersetzungen
- Apollonios: Die Kegelschnitte. Übers. von Arthur Czwalina. Wissenschaftliche Buchgesellschaft, Darmstadt 1967
- Apollonius: Conics, books V to VII. The Arabic translation of the lost Greek original in the version of the Banū Mūsā. In two volumes. Ed. with transl. and commentary by G. J. Toomer. Springer, New York, Berlin, Heidelberg, Springer (Sources in the history of mathematics and physical sciences, 9). ISBN 3-540-97216-1
- Michael Fried: Edmond Halley's Reconstruction of the Lost Book of Apollonius's Conics: Translation and Commentary., Springer, New York, 2011. ISBN 978-1-4614-0145-2 (Rekonstruktion von Buch VIII der Kegelschnitte)
- Apollonios Treatise on conic sections, englische Übersetzung, Herausgabe und Kommentar von Thomas Heath, Cambridge 1896, Oxford 1961
- Paul ver Eecke Les coniques de Apollonios, Brüssel 1924 (französische Übersetzung)
- Robert Catesby Taliaferro (Übersetzer): Apollonios of Perga: Conics Book I-III, Santa Fe: Green Lion Press 1998
- Michael N. Fried (Übersetzer): Apollonius of Perga: Conics Book IV, Santa Fe 2002
- M. N. Fried, Sabetai Unguru Apollonius of Perga's 'Conica': Text, Context, Subtext, Leiden: Brill 2001
- Roshdi Rashed, M. Decorps-Foulquier, M. Federspiel (Übersetzer und Herausgeber) Apollonius de Perge, Coniques: Texte grec et arabe etabli, traduit et commenté, De Gruyter 2008–2010 (französische Übersetzung und griechischer bzw. arabischer Text)
- Ausgabe des Griechischen Texts der ersten vier Bücher (sowie Fragmenten und dem Kommentar von Eutokios) von Heiberg, Leipzig, Teubner 1891, 1893 (2 Bände): Apollonius Pergaeus, quae Graece extant, cum commemtariis antiquis
Literatur
Übersichtsdarstellungen in Handbüchern
- Friedrich Hultsch: Apollonios (112) von Perge. In: Paulys Realencyclopädie der classischen Altertumswissenschaft (RE). Band II,1, Stuttgart 1895, Sp. 151–161 (veraltet).
- Gerald J. Toomer: Apollonius of Perga. In: Charles Coulston Gillispie (Hrsg.): Dictionary of Scientific Biography. Band 1: Pierre Abailard – L. S. Berg. Charles Scribner’s Sons, New York 1970, S. 179–193.
- Hans-Joachim Waschkies: Apollonios aus Perga. In: Hellmut Flashar (Hrsg.): Grundriss der Geschichte der Philosophie. Die Philosophie der Antike, Band 2/1, Schwabe, Basel 1998, ISBN 3-7965-1036-1, S. 400–405
Untersuchungen
- Bartel Leendert van der Waerden: Erwachende Wissenschaft, Birkhäuser 1956, S. 395–436
- Thomas Heath: History of Greek Mathematics, 2 Bände, Oxford 1921
- Otto Neugebauer: Apollonios Studien (= Quellen und Studien zur Geschichte der Mathematik B, Band 2), 1932, S. 215–254
- Otto Neugebauer: The equivalence of eccentric and epicyclic motion according to Apollonius, Scripta Math., Band 24, 1959, S. 5–21
- Otto Neugebauer: Apollonius planetary theory, Comm. Pure Appl. Math., Band 8, 1955, S. 641–648
- Jan Hogendijk: Arabic traces of lost works of Apollonios, Arch. Hist. Exact Sci., Band 35, 1986, S. 187–253
- Jan P. Hogendijk (Hrsg.): Ibn al-Haytham's Completion of the "Conics". New York: Springer Verlag 1985
- Jan P. Hogendijk: Desargues Brouillon project and the Conics of Apollonius, Centaurus, Band 34, 1991, S. 1–43
- Kilian Josef Fleischer: Dionysios von Alexandria. De natura (περὶ φύσεως). Übersetzung, Kommentar und Würdigung. Turnhout 2016, S. 60–70 (zur Biographie und Datierung des Apollonios)
Weblinks
- John J. O’Connor, Edmund F. Robertson: Apollonios von Perge. In: MacTutor History of Mathematics archive.
- Literatur von und über Apollonios von Perge im Katalog der Deutschen Nationalbibliothek
- Links auf Online Ausgaben
- Spektrum.de: Apollonius von Perge (262–190 v. Chr.) 1. April 2012
- Paul Heinrich Balsam: Sieben Bücher über Kegelschnitte, nebst dem durch Halley wieder hergestellten achten Buche, Berlin: Reimer 1861, Internet Archive
Einzelnachweise
- K. Fleischer, Dionysios von Alexandria. De natura (περὶ φύσεως). Übersetzung, Kommentar und Würdigung. Mit einer Einleitung zur Geschichte des Epikureismus in Alexandria, Turnhout, 2016, S. 60–70.
- Fleischer (2016), S. 65–69.
- P. Fraser, Ptolemaic Alexandria, Oxford, 1972, S. 417,418
- Zeuthen: Die Lehre von den Kegelschnitten im Altertum, Denkschr. d.Kopenhagener Akademie 1885, deutsch von Fischer-Benzon, Kopenhagen 1886, in A.Brill, M.Nöther: Bericht über die Entwicklung der algebraischen Funktionen in älterer und neuerer Zeit, Jahresbericht der Deutschen Mathematiker-Vereinigung, Zeitschriftenband (1894)
- van der Waerden: Ausgleichspunkt, „Methode der Perser“ und indische Planetenrechnung
- Versuche zur Rekonstruktion unternahmen François Viète in seinem Apollonius Gallus (1600) und Johann Wilhelm Camerer (1796)
- Einen Rekonstruktionsversuch unternahm Robert Simson 1749